期末真题重组练习卷(二)(含答案)-2024-2025学年数学八年级下册北师大版
文档属性
| 名称 | 期末真题重组练习卷(二)(含答案)-2024-2025学年数学八年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 05:55:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷(二)-2024-2025学年数学八年级下册北师大版
一.选择题(共8小题)
1.(2023春 昌平区期末)中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是( )
A.京剧脸谱 B.剪纸对鱼
C.中国结 D.风筝燕归来
2.(2024秋 恩施市期末)下列说法错误的是( )
A.当x=2时,分式无意义
B.当x>5时,分式的值为正数
C.当分式时,m=±3
D.分式与的最简公分母是3ab2
3.(2024秋 利津县期末)如图, ABCD的对角线AC、BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=7,则EO的长为( )
A.3 B.2 C.1 D.1.5
4.(2024秋 丽水期末)下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
5.(2024秋 安顺期末)某校为满足学生课外活动多样化的需求,欲购买排球和足球若干个.已知足球的单价比排球的单价高60%,用500元购买的排球数量比用720元购买的足球数量多1个,求排球和足球的单价各是多少元?小宇同学根据题意得到方程,则方程中未知数x所表示的是( )
A.足球的单价 B.排球的单价
C.足球的数量 D.排球的数量
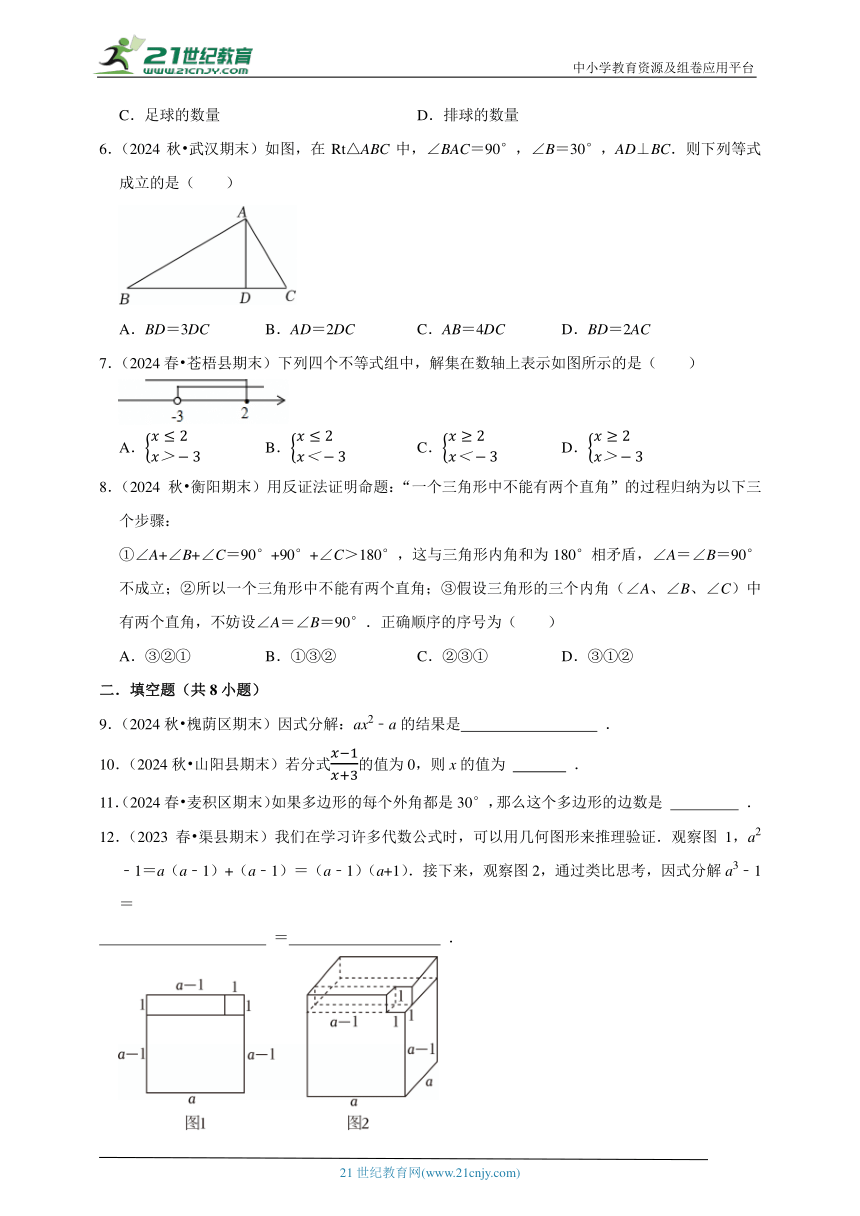
6.(2024秋 武汉期末)如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AD⊥BC.则下列等式成立的是( )
A.BD=3DC B.AD=2DC C.AB=4DC D.BD=2AC
7.(2024春 苍梧县期末)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
8.(2024秋 衡阳期末)用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,∠A=∠B=90°不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角(∠A、∠B、∠C)中有两个直角,不妨设∠A=∠B=90°.正确顺序的序号为( )
A.③②① B.①③② C.②③① D.③①②
二.填空题(共8小题)
9.(2024秋 槐荫区期末)因式分解:ax2﹣a的结果是 .
10.(2024秋 山阳县期末)若分式的值为0,则x的值为 .
11.(2024春 麦积区期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 .
12.(2023春 渠县期末)我们在学习许多代数公式时,可以用几何图形来推理验证.观察图1,a2﹣1=a(a﹣1)+(a﹣1)=(a﹣1)(a+1).接下来,观察图2,通过类比思考,因式分解a3﹣1=
= .
13.(2024秋 仙居县期末)在平面直角坐标系中,点(2,﹣1)关于原点对称的点的坐标是 .
14.(2023春 藁城区期末)如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为 .
15.(2024春 薛城区期末)如图,在△ABC中,AB=BC=4,BD平分∠ABC交AC于点D,点F在BC上,且BF=1,连接AF,E为AF的中点,连接DE,则DE的长为 .
16.(2024秋 海港区期末)已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止,当t= 时,△PBQ是直角三角形.
三.解答题(共8小题)
17.(2024春 淮安期末)解方程:
(1);
(2).
18.(2024春 淮安区期末)先化简,再求值,请你从﹣3、0、2、3中找一个合适的a值代入求值.
19.(2024春 长海县期末)如图,在平行四边形ABCD中,点E和点F分别在边AD,BC上,且∠BAF=∠DCE.求证:四边形AFCE是平行四边形.
20.(2023秋 邵阳期末)如图,在△ABC中,AC=BC,点F为AB的中点,边AC的垂直平分线交AC,CF,CB于点D,O,E,连接OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求∠BOE的度数.
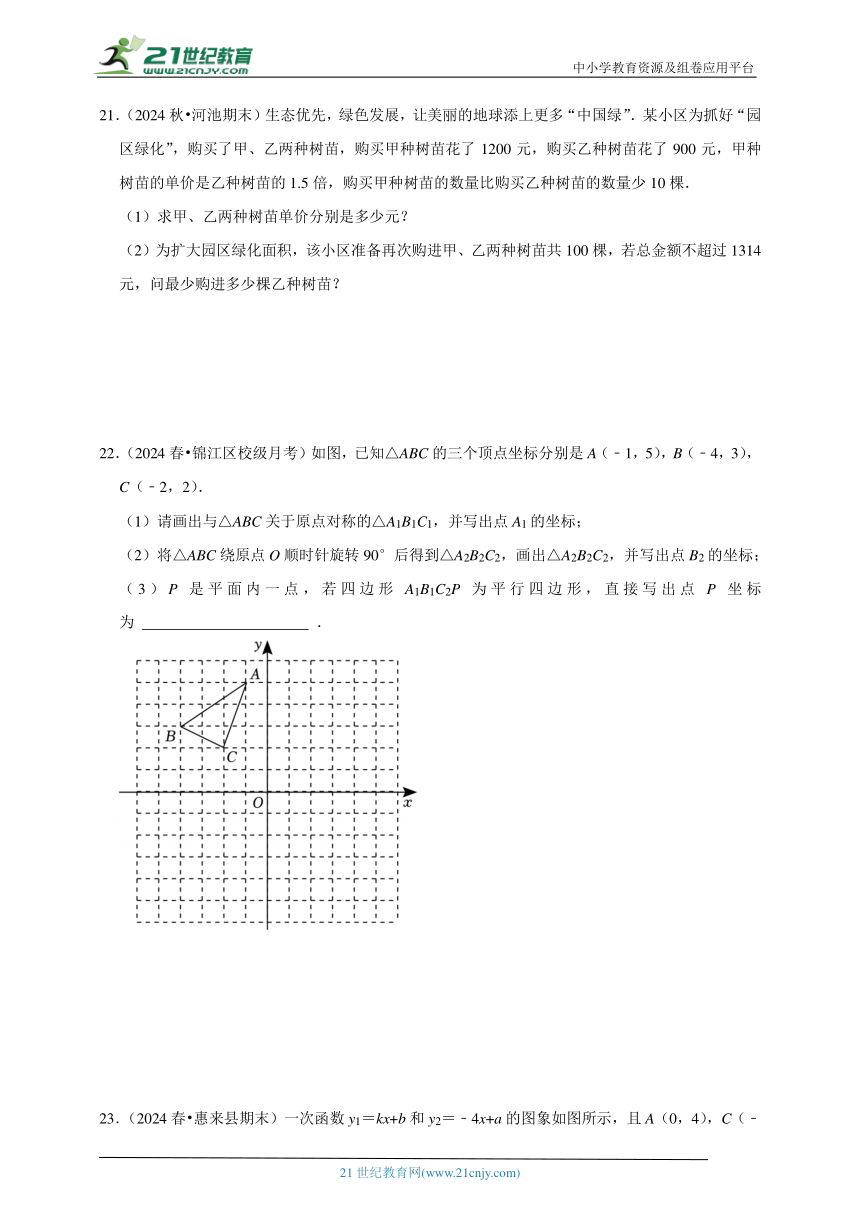
21.(2024秋 河池期末)生态优先,绿色发展,让美丽的地球添上更多“中国绿”.某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的1.5倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.
(1)求甲、乙两种树苗单价分别是多少元?
(2)为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?
22.(2024春 锦江区校级月考)如图,已知△ABC的三个顶点坐标分别是A(﹣1,5),B(﹣4,3),C(﹣2,2).
(1)请画出与△ABC关于原点对称的△A1B1C1,并写出点A1的坐标;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,画出△A2B2C2,并写出点B2的坐标;
(3)P是平面内一点,若四边形A1B1C2P为平行四边形,直接写出点P坐标为 .
23.(2024春 惠来县期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)根据图象可得,不等式kx+b>4的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1;
①求点B的坐标;
②写出不等式组﹣4x+a>kx+b>0的解集 .
24.(2022春 惠来县期末)如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
期末真题重组练习卷(二)-2024-2025学年数学八年级下册北师大版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C C D C B A A D
一.选择题(共8小题)
1.(2023春 昌平区期末)中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是( )
A.京剧脸谱 B.剪纸对鱼
C.中国结 D.风筝燕归来
【解答】解:A、该图形是轴对称图形,不是中心对称图形,不符合题意;
B、该图形不是轴对称图形,是中心对称图形,不符符合题意;
C、该图形既是轴对称图形,又是中心对称图形,符合题意;
D、该图形是既不是轴对称图形,不是中心对称图形,不符合题意.
故选:C.
2.(2024秋 恩施市期末)下列说法错误的是( )
A.当x=2时,分式无意义
B.当x>5时,分式的值为正数
C.当分式时,m=±3
D.分式与的最简公分母是3ab2
【解答】解:A、当x=2时,分式无意义,故本选项说法正确,不符合题意;
B、当x>5时,分式的值为正数,故本选项说法正确,不符合题意;
C、当分式时,m=3,故本选项说法错误,符合题意;
D、分式与的最简公分母是3ab2,故本选项说法正确,不符合题意;
故选:C.
3.(2024秋 利津县期末)如图, ABCD的对角线AC、BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=7,则EO的长为( )
A.3 B.2 C.1 D.1.5
【解答】解:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=7,DO=OB,
∴∠APD=∠CDP,
∵DP平分∠ADC,
∴∠ADP=∠CDP,
∴∠ADP=∠APD,
∴AP=AD=4,
∴PB=AB﹣AP=7﹣4=3,
∵O是BD中点,E是PD中点,
∴OE是△DPB的中位线,
∴OEPB=1.5.
故选:D.
4.(2024秋 丽水期末)下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
【解答】解:A、62+82=102,故是直角三角形,故此选项不合题意;
B、242+72=252,故是直角三角形,故此选项不合题意;
C、22+1.52≠32,故不是直角三角形,故此选项符合题意;
D、92+122=152,故是直角三角形,故此选项不合题意.
故选:C.
5.(2024秋 安顺期末)某校为满足学生课外活动多样化的需求,欲购买排球和足球若干个.已知足球的单价比排球的单价高60%,用500元购买的排球数量比用720元购买的足球数量多1个,求排球和足球的单价各是多少元?小宇同学根据题意得到方程,则方程中未知数x所表示的是( )
A.足球的单价 B.排球的单价
C.足球的数量 D.排球的数量
【解答】解:∵足球的单价比排球的单价高60%,用500元购买的排球数量比用720元购买的足球数量多1个,,
∴方程中未知数x所表示的是排球的单价,
故选:B.
6.(2024秋 武汉期末)如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AD⊥BC.则下列等式成立的是( )
A.BD=3DC B.AD=2DC C.AB=4DC D.BD=2AC
【解答】解:∵∠BAC=90°,∠B=30°,
∴BC=2AC,∠C=60°,
∵AD⊥BC,
∴∠DAC=30°,
∴AC=2DC,
∴B不符合要求;
∴BC=4DC,
∴C不符合要求;
∴BD=3DC,
∴A符合要求;
∵AC=2DC,BC=4DC
∴BDAC,
∴D不符合要求;
故选:A.
7.(2024春 苍梧县期末)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
【解答】解:由解集在数轴上的表示可知,该不等式组为,
故选:A.
8.(2024秋 衡阳期末)用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,∠A=∠B=90°不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角(∠A、∠B、∠C)中有两个直角,不妨设∠A=∠B=90°.正确顺序的序号为( )
A.③②① B.①③② C.②③① D.③①②
【解答】解:反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
假设三角形的三个内角(∠A、∠B、∠C)中有两个直角,不妨设∠A=∠B=90°;
则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角,
故选:D.
二.填空题(共8小题)
9.(2024秋 槐荫区期末)因式分解:ax2﹣a的结果是 a(x+1)(x﹣1) .
【解答】解:原式=a(x2﹣1)=a(x+1)(x﹣1),
故答案为:a(x+1)(x﹣1)
10.(2024秋 山阳县期末)若分式的值为0,则x的值为 1 .
【解答】解:∵分式的值为0,
∵x﹣1=0且x+3≠0,
∴x=1,
当x=1时x+3≠0,
∴当x=1时,分式的值是0.
故答案为:1.
11.(2024春 麦积区期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 12 .
【解答】解:多边形的边数是:360°÷30°=12.
故答案为:12.
12.(2023春 渠县期末)我们在学习许多代数公式时,可以用几何图形来推理验证.观察图1,a2﹣1=a(a﹣1)+(a﹣1)=(a﹣1)(a+1).接下来,观察图2,通过类比思考,因式分解a3﹣1= a2(a﹣1)+a(a﹣1)+(a﹣1) = (a﹣1)(a2+a+1) .
【解答】解:将图2看作三个长方体相加时,可得式子:a×a×(a﹣1)+1×1×(a﹣1)+1×a×(a﹣1)=a2(a﹣1)+a(a﹣1)+(a﹣1);
原式两边提取a﹣1,可得原式=(a﹣1)(a2+a+1).
故答案为:a2(a﹣1)+a(a﹣1)+(a﹣1);(a﹣1)(a2+a+1).
13.(2024秋 仙居县期末)在平面直角坐标系中,点(2,﹣1)关于原点对称的点的坐标是 (﹣2,1) .
【解答】解:点(2,﹣1)关于原点对称的点的坐标是(﹣2,1),
故答案为:(﹣2,1).
14.(2023春 藁城区期末)如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为 x>﹣2 .
【解答】解:观察图象知:当x>﹣2时,kx+b>4,
故答案为x>﹣2.
15.(2024春 薛城区期末)如图,在△ABC中,AB=BC=4,BD平分∠ABC交AC于点D,点F在BC上,且BF=1,连接AF,E为AF的中点,连接DE,则DE的长为 .
【解答】解:∵BC=4,BF=1,
∴FC=BC﹣BF=4﹣1=3,
∵AB=BC,BD平分∠ABC,
∴AD=DC,
∵AE=EF,
∴DE是△AFC的中位线,
∴.
故答案为:.
16.(2024秋 海港区期末)已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止,当t= 1或2 时,△PBQ是直角三角形.
【解答】解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=3﹣t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQBP,
即t(3﹣t),t=1(秒),
当∠BPQ=90°时,BPBQ,
3﹣tt,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
故答案为:1或2.
三.解答题(共8小题)
17.(2024春 淮安期末)解方程:
(1);
(2).
【解答】解:(1),
去分母得:x+3=4x,
移项得:x﹣4x=﹣3,
合并同类项得:﹣3x=﹣3,
解得:x=1,
经检验x=1是分式方程的解;
(2),
去分母得:1+3(x﹣2)=x﹣1
去括号得:1+3x﹣6=x﹣1,
移项得:3x﹣x=﹣1﹣1+6,
合并同类项得:2x=4,
系数化为1得:x=2,
经检验x=2是增根,原分式方程无解.
18.(2024春 淮安区期末)先化简,再求值,请你从﹣3、0、2、3中找一个合适的a值代入求值.
【解答】解:原式
,
当a=0时,原式.
19.(2024春 长海县期末)如图,在平行四边形ABCD中,点E和点F分别在边AD,BC上,且∠BAF=∠DCE.求证:四边形AFCE是平行四边形.
【解答】证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,BC=AD,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(ASA),
∴AF=CE,BF=DE,
∴BC﹣BF=AD﹣DE,
即CF=AE,
∴四边形AFCE是平行四边形.
20.(2023秋 邵阳期末)如图,在△ABC中,AC=BC,点F为AB的中点,边AC的垂直平分线交AC,CF,CB于点D,O,E,连接OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求∠BOE的度数.
【解答】(1)证明:连接OA,如图,
∵AC=BC,点F为AB的中点,
∴CF⊥AB,
∴CF垂直平分AB,
∴OA=OB,
∵DE垂直平分AC,
∴OA=OC,
∴OB=OC,
∴△OBC为等腰三角形;
(2)解:∵CA=CB,CF⊥AB,
∴CF平分∠ACB,
∴∠BCF=∠ACF=23°,
∵OB=OC,
∴∠OBC=∠OCB=23°,
∵∠EDC=90°
∴∠DEC=90°﹣∠DCE=90°﹣23°﹣23°=44°,
∵∠OEC=∠OBE+∠BOE,
∴∠BOE=44°﹣23°=21°.
21.(2024秋 河池期末)生态优先,绿色发展,让美丽的地球添上更多“中国绿”.某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的1.5倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.
(1)求甲、乙两种树苗单价分别是多少元?
(2)为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?
【解答】解:(1)设乙种树苗单价是x元,则甲种树苗单价是1.5x元,
依题意得:10,
解得:x=10,
经检验,x=10是原方程的解,且符合题意,
∴1.5x=1.5×10=15,
答:甲种树苗单价是15元,乙种树苗单价是10元;
(2)设购进乙种树苗m棵,则购进甲种树苗(100﹣m)棵,
依题意得:10m+15(100﹣m)≤1314,
解得:m≥37.2,
又∵m为整数,
∴m的最,小值为38,
答:最少购进38棵乙种树苗.
22.(2024春 锦江区校级月考)如图,已知△ABC的三个顶点坐标分别是A(﹣1,5),B(﹣4,3),C(﹣2,2).
(1)请画出与△ABC关于原点对称的△A1B1C1,并写出点A1的坐标;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,画出△A2B2C2,并写出点B2的坐标;
(3)P是平面内一点,若四边形A1B1C2P为平行四边形,直接写出点P坐标为 (3,﹣10)或(﹣1,0)或(5,4) .
【解答】解:(1)如图,△A1B1C1即为所求.
由图可得,点A1的坐标为(1,﹣5).
(2)如图,△A2B2C2即为所求.
由图可得,点B2的坐标为(3,4).
(3)当以A1B1为对角线时,点P的坐标为(3,﹣10);
当以A1C2为对角线时,点P的坐标为(﹣1,0);
当以B1C2为对角线时,点P的坐标为(5,4).
∴点P坐标为(3,﹣10)或(﹣1,0)或(5,4).
23.(2024春 惠来县期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)根据图象可得,不等式kx+b>4的解集是 x>0 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1;
①求点B的坐标;
②写出不等式组﹣4x+a>kx+b>0的解集 ﹣2<x<1 .
【解答】解:(1)根据图象可得,不等式kx+b>4的解集是x>0,
故答案为:x>0;
(2)①∵A(0,4),C(﹣2,0)在一次函数y1=kx+b上,
∴,得,
∴一次函数y1=2x+4,
∵不等式kx+b>﹣4x+a的解集是x>1,
∴点B的横坐标是x=1,
当x=1时,y1=2×1+4=6,
∴点B的坐标为(1,6);
②∵点B的坐标为(1,6);C(﹣2,0)
根据函数图象可得:﹣4x+a>kx+b>0的解集为﹣2<x<1,
故答案为:﹣2<x<1.
24.(2022春 惠来县期末)如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= 6 ;
(2)当t= 8 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
【解答】解:(1)BP=2t=2×3=6,
故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,
∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;
故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,
S△ABPBP×AB2t×4=4t;(0<t<4);
②当点P在CD上运动时,
S△ABPAB×BC4×8=16;(4≤t≤6);
③当点P在AD上运动时,
S△ABPAB×AP4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,
∴点P到AB边的距离也为4,
即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,
∴点P到DE边的距离也为4,
∴PE=DE=5,
∴PC=PE﹣CE=2,
∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,
即PC=PH,
∵PC=2t﹣8,
∵S△DCE=S△DPE+S△PCE,
∴3×45×PH3×PC,
∴12=8PH,
∴12=8(2t﹣8),
解得t.
综上所述:t=2或t=3或t时,点P到四边形ABED相邻两边距离相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷(二)-2024-2025学年数学八年级下册北师大版
一.选择题(共8小题)
1.(2023春 昌平区期末)中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是( )
A.京剧脸谱 B.剪纸对鱼
C.中国结 D.风筝燕归来
2.(2024秋 恩施市期末)下列说法错误的是( )
A.当x=2时,分式无意义
B.当x>5时,分式的值为正数
C.当分式时,m=±3
D.分式与的最简公分母是3ab2
3.(2024秋 利津县期末)如图, ABCD的对角线AC、BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=7,则EO的长为( )
A.3 B.2 C.1 D.1.5
4.(2024秋 丽水期末)下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
5.(2024秋 安顺期末)某校为满足学生课外活动多样化的需求,欲购买排球和足球若干个.已知足球的单价比排球的单价高60%,用500元购买的排球数量比用720元购买的足球数量多1个,求排球和足球的单价各是多少元?小宇同学根据题意得到方程,则方程中未知数x所表示的是( )
A.足球的单价 B.排球的单价
C.足球的数量 D.排球的数量
6.(2024秋 武汉期末)如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AD⊥BC.则下列等式成立的是( )
A.BD=3DC B.AD=2DC C.AB=4DC D.BD=2AC
7.(2024春 苍梧县期末)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
8.(2024秋 衡阳期末)用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,∠A=∠B=90°不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角(∠A、∠B、∠C)中有两个直角,不妨设∠A=∠B=90°.正确顺序的序号为( )
A.③②① B.①③② C.②③① D.③①②
二.填空题(共8小题)
9.(2024秋 槐荫区期末)因式分解:ax2﹣a的结果是 .
10.(2024秋 山阳县期末)若分式的值为0,则x的值为 .
11.(2024春 麦积区期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 .
12.(2023春 渠县期末)我们在学习许多代数公式时,可以用几何图形来推理验证.观察图1,a2﹣1=a(a﹣1)+(a﹣1)=(a﹣1)(a+1).接下来,观察图2,通过类比思考,因式分解a3﹣1=
= .
13.(2024秋 仙居县期末)在平面直角坐标系中,点(2,﹣1)关于原点对称的点的坐标是 .
14.(2023春 藁城区期末)如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为 .
15.(2024春 薛城区期末)如图,在△ABC中,AB=BC=4,BD平分∠ABC交AC于点D,点F在BC上,且BF=1,连接AF,E为AF的中点,连接DE,则DE的长为 .
16.(2024秋 海港区期末)已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止,当t= 时,△PBQ是直角三角形.
三.解答题(共8小题)
17.(2024春 淮安期末)解方程:
(1);
(2).
18.(2024春 淮安区期末)先化简,再求值,请你从﹣3、0、2、3中找一个合适的a值代入求值.
19.(2024春 长海县期末)如图,在平行四边形ABCD中,点E和点F分别在边AD,BC上,且∠BAF=∠DCE.求证:四边形AFCE是平行四边形.
20.(2023秋 邵阳期末)如图,在△ABC中,AC=BC,点F为AB的中点,边AC的垂直平分线交AC,CF,CB于点D,O,E,连接OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求∠BOE的度数.
21.(2024秋 河池期末)生态优先,绿色发展,让美丽的地球添上更多“中国绿”.某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的1.5倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.
(1)求甲、乙两种树苗单价分别是多少元?
(2)为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?
22.(2024春 锦江区校级月考)如图,已知△ABC的三个顶点坐标分别是A(﹣1,5),B(﹣4,3),C(﹣2,2).
(1)请画出与△ABC关于原点对称的△A1B1C1,并写出点A1的坐标;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,画出△A2B2C2,并写出点B2的坐标;
(3)P是平面内一点,若四边形A1B1C2P为平行四边形,直接写出点P坐标为 .
23.(2024春 惠来县期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)根据图象可得,不等式kx+b>4的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1;
①求点B的坐标;
②写出不等式组﹣4x+a>kx+b>0的解集 .
24.(2022春 惠来县期末)如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
期末真题重组练习卷(二)-2024-2025学年数学八年级下册北师大版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C C D C B A A D
一.选择题(共8小题)
1.(2023春 昌平区期末)中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是( )
A.京剧脸谱 B.剪纸对鱼
C.中国结 D.风筝燕归来
【解答】解:A、该图形是轴对称图形,不是中心对称图形,不符合题意;
B、该图形不是轴对称图形,是中心对称图形,不符符合题意;
C、该图形既是轴对称图形,又是中心对称图形,符合题意;
D、该图形是既不是轴对称图形,不是中心对称图形,不符合题意.
故选:C.
2.(2024秋 恩施市期末)下列说法错误的是( )
A.当x=2时,分式无意义
B.当x>5时,分式的值为正数
C.当分式时,m=±3
D.分式与的最简公分母是3ab2
【解答】解:A、当x=2时,分式无意义,故本选项说法正确,不符合题意;
B、当x>5时,分式的值为正数,故本选项说法正确,不符合题意;
C、当分式时,m=3,故本选项说法错误,符合题意;
D、分式与的最简公分母是3ab2,故本选项说法正确,不符合题意;
故选:C.
3.(2024秋 利津县期末)如图, ABCD的对角线AC、BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=7,则EO的长为( )
A.3 B.2 C.1 D.1.5
【解答】解:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=7,DO=OB,
∴∠APD=∠CDP,
∵DP平分∠ADC,
∴∠ADP=∠CDP,
∴∠ADP=∠APD,
∴AP=AD=4,
∴PB=AB﹣AP=7﹣4=3,
∵O是BD中点,E是PD中点,
∴OE是△DPB的中位线,
∴OEPB=1.5.
故选:D.
4.(2024秋 丽水期末)下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
【解答】解:A、62+82=102,故是直角三角形,故此选项不合题意;
B、242+72=252,故是直角三角形,故此选项不合题意;
C、22+1.52≠32,故不是直角三角形,故此选项符合题意;
D、92+122=152,故是直角三角形,故此选项不合题意.
故选:C.
5.(2024秋 安顺期末)某校为满足学生课外活动多样化的需求,欲购买排球和足球若干个.已知足球的单价比排球的单价高60%,用500元购买的排球数量比用720元购买的足球数量多1个,求排球和足球的单价各是多少元?小宇同学根据题意得到方程,则方程中未知数x所表示的是( )
A.足球的单价 B.排球的单价
C.足球的数量 D.排球的数量
【解答】解:∵足球的单价比排球的单价高60%,用500元购买的排球数量比用720元购买的足球数量多1个,,
∴方程中未知数x所表示的是排球的单价,
故选:B.
6.(2024秋 武汉期末)如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AD⊥BC.则下列等式成立的是( )
A.BD=3DC B.AD=2DC C.AB=4DC D.BD=2AC
【解答】解:∵∠BAC=90°,∠B=30°,
∴BC=2AC,∠C=60°,
∵AD⊥BC,
∴∠DAC=30°,
∴AC=2DC,
∴B不符合要求;
∴BC=4DC,
∴C不符合要求;
∴BD=3DC,
∴A符合要求;
∵AC=2DC,BC=4DC
∴BDAC,
∴D不符合要求;
故选:A.
7.(2024春 苍梧县期末)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. B. C. D.
【解答】解:由解集在数轴上的表示可知,该不等式组为,
故选:A.
8.(2024秋 衡阳期末)用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,∠A=∠B=90°不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角(∠A、∠B、∠C)中有两个直角,不妨设∠A=∠B=90°.正确顺序的序号为( )
A.③②① B.①③② C.②③① D.③①②
【解答】解:反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
假设三角形的三个内角(∠A、∠B、∠C)中有两个直角,不妨设∠A=∠B=90°;
则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角,
故选:D.
二.填空题(共8小题)
9.(2024秋 槐荫区期末)因式分解:ax2﹣a的结果是 a(x+1)(x﹣1) .
【解答】解:原式=a(x2﹣1)=a(x+1)(x﹣1),
故答案为:a(x+1)(x﹣1)
10.(2024秋 山阳县期末)若分式的值为0,则x的值为 1 .
【解答】解:∵分式的值为0,
∵x﹣1=0且x+3≠0,
∴x=1,
当x=1时x+3≠0,
∴当x=1时,分式的值是0.
故答案为:1.
11.(2024春 麦积区期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 12 .
【解答】解:多边形的边数是:360°÷30°=12.
故答案为:12.
12.(2023春 渠县期末)我们在学习许多代数公式时,可以用几何图形来推理验证.观察图1,a2﹣1=a(a﹣1)+(a﹣1)=(a﹣1)(a+1).接下来,观察图2,通过类比思考,因式分解a3﹣1= a2(a﹣1)+a(a﹣1)+(a﹣1) = (a﹣1)(a2+a+1) .
【解答】解:将图2看作三个长方体相加时,可得式子:a×a×(a﹣1)+1×1×(a﹣1)+1×a×(a﹣1)=a2(a﹣1)+a(a﹣1)+(a﹣1);
原式两边提取a﹣1,可得原式=(a﹣1)(a2+a+1).
故答案为:a2(a﹣1)+a(a﹣1)+(a﹣1);(a﹣1)(a2+a+1).
13.(2024秋 仙居县期末)在平面直角坐标系中,点(2,﹣1)关于原点对称的点的坐标是 (﹣2,1) .
【解答】解:点(2,﹣1)关于原点对称的点的坐标是(﹣2,1),
故答案为:(﹣2,1).
14.(2023春 藁城区期末)如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为 x>﹣2 .
【解答】解:观察图象知:当x>﹣2时,kx+b>4,
故答案为x>﹣2.
15.(2024春 薛城区期末)如图,在△ABC中,AB=BC=4,BD平分∠ABC交AC于点D,点F在BC上,且BF=1,连接AF,E为AF的中点,连接DE,则DE的长为 .
【解答】解:∵BC=4,BF=1,
∴FC=BC﹣BF=4﹣1=3,
∵AB=BC,BD平分∠ABC,
∴AD=DC,
∵AE=EF,
∴DE是△AFC的中位线,
∴.
故答案为:.
16.(2024秋 海港区期末)已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止,当t= 1或2 时,△PBQ是直角三角形.
【解答】解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=3﹣t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQBP,
即t(3﹣t),t=1(秒),
当∠BPQ=90°时,BPBQ,
3﹣tt,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
故答案为:1或2.
三.解答题(共8小题)
17.(2024春 淮安期末)解方程:
(1);
(2).
【解答】解:(1),
去分母得:x+3=4x,
移项得:x﹣4x=﹣3,
合并同类项得:﹣3x=﹣3,
解得:x=1,
经检验x=1是分式方程的解;
(2),
去分母得:1+3(x﹣2)=x﹣1
去括号得:1+3x﹣6=x﹣1,
移项得:3x﹣x=﹣1﹣1+6,
合并同类项得:2x=4,
系数化为1得:x=2,
经检验x=2是增根,原分式方程无解.
18.(2024春 淮安区期末)先化简,再求值,请你从﹣3、0、2、3中找一个合适的a值代入求值.
【解答】解:原式
,
当a=0时,原式.
19.(2024春 长海县期末)如图,在平行四边形ABCD中,点E和点F分别在边AD,BC上,且∠BAF=∠DCE.求证:四边形AFCE是平行四边形.
【解答】证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,BC=AD,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(ASA),
∴AF=CE,BF=DE,
∴BC﹣BF=AD﹣DE,
即CF=AE,
∴四边形AFCE是平行四边形.
20.(2023秋 邵阳期末)如图,在△ABC中,AC=BC,点F为AB的中点,边AC的垂直平分线交AC,CF,CB于点D,O,E,连接OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求∠BOE的度数.
【解答】(1)证明:连接OA,如图,
∵AC=BC,点F为AB的中点,
∴CF⊥AB,
∴CF垂直平分AB,
∴OA=OB,
∵DE垂直平分AC,
∴OA=OC,
∴OB=OC,
∴△OBC为等腰三角形;
(2)解:∵CA=CB,CF⊥AB,
∴CF平分∠ACB,
∴∠BCF=∠ACF=23°,
∵OB=OC,
∴∠OBC=∠OCB=23°,
∵∠EDC=90°
∴∠DEC=90°﹣∠DCE=90°﹣23°﹣23°=44°,
∵∠OEC=∠OBE+∠BOE,
∴∠BOE=44°﹣23°=21°.
21.(2024秋 河池期末)生态优先,绿色发展,让美丽的地球添上更多“中国绿”.某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的1.5倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.
(1)求甲、乙两种树苗单价分别是多少元?
(2)为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?
【解答】解:(1)设乙种树苗单价是x元,则甲种树苗单价是1.5x元,
依题意得:10,
解得:x=10,
经检验,x=10是原方程的解,且符合题意,
∴1.5x=1.5×10=15,
答:甲种树苗单价是15元,乙种树苗单价是10元;
(2)设购进乙种树苗m棵,则购进甲种树苗(100﹣m)棵,
依题意得:10m+15(100﹣m)≤1314,
解得:m≥37.2,
又∵m为整数,
∴m的最,小值为38,
答:最少购进38棵乙种树苗.
22.(2024春 锦江区校级月考)如图,已知△ABC的三个顶点坐标分别是A(﹣1,5),B(﹣4,3),C(﹣2,2).
(1)请画出与△ABC关于原点对称的△A1B1C1,并写出点A1的坐标;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,画出△A2B2C2,并写出点B2的坐标;
(3)P是平面内一点,若四边形A1B1C2P为平行四边形,直接写出点P坐标为 (3,﹣10)或(﹣1,0)或(5,4) .
【解答】解:(1)如图,△A1B1C1即为所求.
由图可得,点A1的坐标为(1,﹣5).
(2)如图,△A2B2C2即为所求.
由图可得,点B2的坐标为(3,4).
(3)当以A1B1为对角线时,点P的坐标为(3,﹣10);
当以A1C2为对角线时,点P的坐标为(﹣1,0);
当以B1C2为对角线时,点P的坐标为(5,4).
∴点P坐标为(3,﹣10)或(﹣1,0)或(5,4).
23.(2024春 惠来县期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)根据图象可得,不等式kx+b>4的解集是 x>0 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1;
①求点B的坐标;
②写出不等式组﹣4x+a>kx+b>0的解集 ﹣2<x<1 .
【解答】解:(1)根据图象可得,不等式kx+b>4的解集是x>0,
故答案为:x>0;
(2)①∵A(0,4),C(﹣2,0)在一次函数y1=kx+b上,
∴,得,
∴一次函数y1=2x+4,
∵不等式kx+b>﹣4x+a的解集是x>1,
∴点B的横坐标是x=1,
当x=1时,y1=2×1+4=6,
∴点B的坐标为(1,6);
②∵点B的坐标为(1,6);C(﹣2,0)
根据函数图象可得:﹣4x+a>kx+b>0的解集为﹣2<x<1,
故答案为:﹣2<x<1.
24.(2022春 惠来县期末)如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= 6 ;
(2)当t= 8 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
【解答】解:(1)BP=2t=2×3=6,
故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,
∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;
故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,
S△ABPBP×AB2t×4=4t;(0<t<4);
②当点P在CD上运动时,
S△ABPAB×BC4×8=16;(4≤t≤6);
③当点P在AD上运动时,
S△ABPAB×AP4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,
∴点P到AB边的距离也为4,
即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,
∴点P到DE边的距离也为4,
∴PE=DE=5,
∴PC=PE﹣CE=2,
∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,
即PC=PH,
∵PC=2t﹣8,
∵S△DCE=S△DPE+S△PCE,
∴3×45×PH3×PC,
∴12=8PH,
∴12=8(2t﹣8),
解得t.
综上所述:t=2或t=3或t时,点P到四边形ABED相邻两边距离相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
