期末真题重组练习卷(含答案)-2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 期末真题重组练习卷(含答案)-2024-2025学年数学七年级下册苏科版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 981.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2024秋 临漳县期末)下列语句中,不是命题的是( )
A.两点确定一条直线 B.垂线段最短
C.同位角相等 D.作角A的平分线
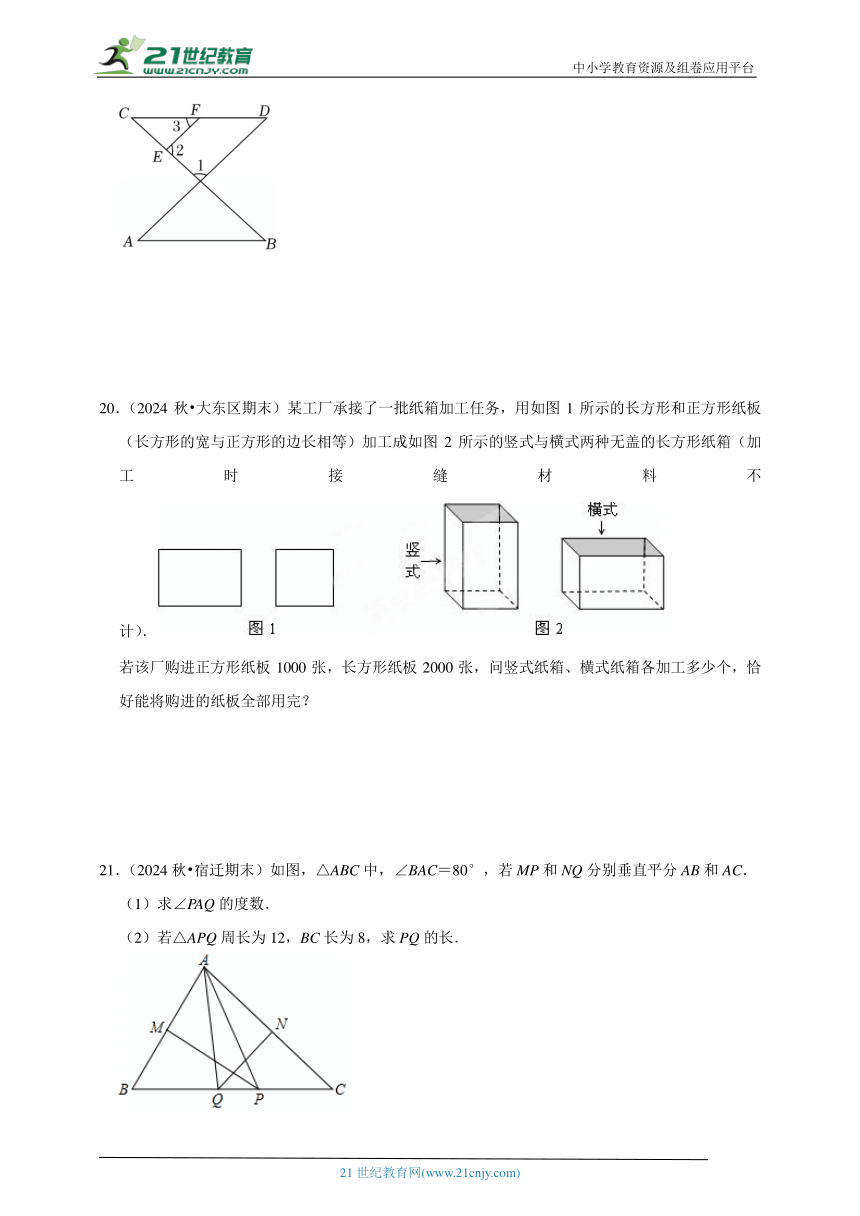
2.(2024春 田家庵区校级期末)已知x>y,下列不等式一定成立的是( )
A.x﹣6<y﹣6 B.2x<2y C.﹣2x>﹣2y D.2x+1>2y+1
3.(2024秋 广饶县期末)《国家宝藏》节目立足于中华文化宝库资源.通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是( )
A. B.
C. D.
4.(2024秋 临漳县期末)解关于x,y的二元一次方程组,将①代入②,消去y后所得到的方程是( )
A.3x+4x﹣3=8 B.3x+4x+3=8 C.3x+4x﹣6=8 D.3x+4x+6=8
5.(2023春 埇桥区校级期末)下列运算中正确的是( )
A.b2 b3=b6 B.(2x+y)2=4x2+y2
C.(﹣3x2y)3=﹣27x6y3 D.x+x=x2
6.(2024春 沙河市期末)解不等式时,去分母后结果正确的为( )
A.2(x+2)>1﹣3(x﹣3) B.2x+4>6﹣3x﹣9
C.2x+4>6﹣3x+3 D.2(x+2)>6﹣3(x﹣3)
7.(2024秋 深圳期末)《四元玉鉴》是一部成就辉煌的数学名著,在中国古代数学史上有着重要地位.其中有一个“酒分醇醨”问题:务中听得语吟吟,亩道醇醨酒二盆.醇酒一升醉三客,醨酒三升醉一人.共通饮了一斗七,一十九客醉醺醺.欲问高明能算士,几何醨酒几多醇?其大意为:有好酒和薄酒分别装在瓶中,好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,试问好酒、薄酒各有多少升?若设好酒有x升,薄酒有y升,根据题意列方程组为( )
A. B.
C. D.
8.(2024秋 雁江区校级期末)从边长为a的大正方形纸板正中央挖去一个边长为b的小正方形后,将其裁成四个大小和形状完全相同的四边形(如图1),然后拼成一个平行四边形(如图2),那么通过计算两个图形阴影部分的面积,可以验证成立的等式为( )
A.a2﹣b2=(a﹣b)2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
二.填空题(共8小题)
9.(2023春 石狮市期末)已知a>b,则﹣2a ﹣2b(填“>”、“<”或“=”号).
10.(2023春 垦利区期末)不等式组的解集为 .
11.(2024春 南宁期末)已知x,y满足方程组,则x﹣y的值为 .
12.(2022春 高新区校级期末)如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一次运算.若运算进行了3次才停止,则x的取值范围是 .
13.(2024秋 榆阳区期末)说明命题“若a>b,则ac>bc”的假命题的一个反例的c的值可以是 .
14.(2024秋 浦东新区期末)小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,请你根据图中的信息,若小明把50个纸杯整齐叠放在一起时,它的高度约是 cm.
15.(2024秋 大名县期末)如图,三角形OAB绕点O逆时针旋转75°到三角形OCD的位置,已知∠AOB=45°,则∠AOD= .
16.(2024春 金华期末)若关于x,y的二元一次方程mx+ny=3有两个解和,则m+n的值为 .
三.解答题(共8小题)
17.(2024春 岳麓区校级期末)解不等式组:.
18.(2024秋 中牟县期末)解方程组:.
19.(2024秋 平果市期末)如图,从①∠1+∠2=180°,②∠3=∠A,③∠B=∠C,三个条件中选出两个作为题设,另一个作为结论可以组成3个命题.从中选择一个真命题,写出已知求证,并证明.
如图,已知 ,求证: .(填“①”,“②”,“③”)
证明:
20.(2024秋 大东区期末)某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸箱、横式纸箱各加工多少个,恰好能将购进的纸板全部用完?
21.(2024秋 宿迁期末)如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.
22.(2024秋 凤阳县期末)新新商场第1次用39万元购进A、B两种商品.销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量).
商品 价格 A B
进价(元/件) 1200 1000
售价(元/件) 1350 1200
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于36000元,则B种商品是打几折销售的?
23.(2024春 榕城区期末)如图,A,B,C三点均在10×10的正方形网格格点上(图中网格线的交点就是格点).
(1)画出将△ABC向右平移4格,再向下平移4格后的△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转180°后的△A2B2C;
(3)在(1)和(2)的条件下,四边形A1B1A2B2是否为中心对称图形?若是,请在图中标出它的对称中心P;若不是,请用所学知识简要说明理由.
24.(2024秋 包头期末)乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片:A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法表示图2大正方形的面积:
方法1: ,
方法2: ;
(2)观察图2,请你写出三个代数式(a+b)2,a2+b2,ab之间的数量关系: ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知a+b=7,a2+b2=33,求ab的值;
②已知(2023﹣a)2+(a﹣2021)2=8,求(2023﹣a)(a﹣2021)的值.
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D D B C C D A D
一.选择题(共8小题)
1.(2024秋 临漳县期末)下列语句中,不是命题的是( )
A.两点确定一条直线 B.垂线段最短
C.同位角相等 D.作角A的平分线
【解答】解:两点确定一条直线,垂线段最短,同位角相等都是命题,而作角A的平分线为描述性语言,它不是命题.
故选:D.
2.(2024春 田家庵区校级期末)已知x>y,下列不等式一定成立的是( )
A.x﹣6<y﹣6 B.2x<2y C.﹣2x>﹣2y D.2x+1>2y+1
【解答】解:A、∵x>y,∴x﹣6>y﹣6,原变形错误,不符合题意;
B、∵x>y,∴2x>2y,原变形错误,不符合题意;
C、∵x>y,∴﹣x<﹣y,∴﹣2x<﹣2y,原变形错误,不符合题意
D、∵x>y,∴2x>2y,∴2x+1>2y+1,正确,符合题意.
故选:D.
3.(2024秋 广饶县期末)《国家宝藏》节目立足于中华文化宝库资源.通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、不是轴对称图形,故此选项不合题意;
B、是轴对称图形,故此选项符合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意;
故选:B.
4.(2024秋 临漳县期末)解关于x,y的二元一次方程组,将①代入②,消去y后所得到的方程是( )
A.3x+4x﹣3=8 B.3x+4x+3=8 C.3x+4x﹣6=8 D.3x+4x+6=8
【解答】解:,
将①代入②,消去y后所得到的方程是3x+2(2x﹣3)=8,
去括号,得3x+4x﹣6=8.
故选:C.
5.(2023春 埇桥区校级期末)下列运算中正确的是( )
A.b2 b3=b6 B.(2x+y)2=4x2+y2
C.(﹣3x2y)3=﹣27x6y3 D.x+x=x2
【解答】解:A、b2 b3=b5,不符合题意;
B、(2x+y)2=4x2+4xy+y2,不符合题意;
C、(﹣3x2y)3=﹣27x6y3,符合题意;
D、x+x=2x,不符合题意.
故选:C.
6.(2024春 沙河市期末)解不等式时,去分母后结果正确的为( )
A.2(x+2)>1﹣3(x﹣3) B.2x+4>6﹣3x﹣9
C.2x+4>6﹣3x+3 D.2(x+2)>6﹣3(x﹣3)
【解答】解:去分母得2(x+2)>6﹣3(x﹣3).
故选:D.
7.(2024秋 深圳期末)《四元玉鉴》是一部成就辉煌的数学名著,在中国古代数学史上有着重要地位.其中有一个“酒分醇醨”问题:务中听得语吟吟,亩道醇醨酒二盆.醇酒一升醉三客,醨酒三升醉一人.共通饮了一斗七,一十九客醉醺醺.欲问高明能算士,几何醨酒几多醇?其大意为:有好酒和薄酒分别装在瓶中,好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,试问好酒、薄酒各有多少升?若设好酒有x升,薄酒有y升,根据题意列方程组为( )
A. B.
C. D.
【解答】解:∵好酒和薄酒一共饮了17升,
∴x+y=17;
∵好酒1升醉了3位客人,薄酒3升醉了1位客人,且共醉了19位客人,
∴3xy=19.
∴根据题意可列方程组.
故选:A.
8.(2024秋 雁江区校级期末)从边长为a的大正方形纸板正中央挖去一个边长为b的小正方形后,将其裁成四个大小和形状完全相同的四边形(如图1),然后拼成一个平行四边形(如图2),那么通过计算两个图形阴影部分的面积,可以验证成立的等式为( )
A.a2﹣b2=(a﹣b)2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
【解答】解:图1中阴影部分的面积为:a2﹣b2,图2中阴影部分的面积为:(a+b)(a﹣b),
∵两图中阴影部分的面积相等,
∴a2﹣b2=(a+b)(a﹣b),
∴可以验证成立的公式为a2﹣b2=(a+b)(a﹣b),
故选:D.
二.填空题(共8小题)
9.(2023春 石狮市期末)已知a>b,则﹣2a < ﹣2b(填“>”、“<”或“=”号).
【解答】解:∵a>b,
∴﹣2a<﹣2b,
故答案为:<.
10.(2023春 垦利区期末)不等式组的解集为 ﹣3<x≤1 .
【解答】解:由x+2≤3得:x≤1,
由1+x>﹣2得:x>﹣3,
则不等式组的解集为﹣3<x≤1,
故答案为:﹣3<x≤1.
11.(2024春 南宁期末)已知x,y满足方程组,则x﹣y的值为 ﹣1 .
【解答】解:,
①﹣②得:x﹣y=﹣1,
故答案为:﹣1
12.(2022春 高新区校级期末)如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一次运算.若运算进行了3次才停止,则x的取值范围是 2<x≤4 .
【解答】解:依题意得:,
解得:2<x≤4,
故答案为:2<x≤4.
13.(2024秋 榆阳区期末)说明命题“若a>b,则ac>bc”的假命题的一个反例的c的值可以是 0 .
【解答】解:若a>b,当c=0时ac=bc=0,
故答案为:0(答案不唯一).
14.(2024秋 浦东新区期末)小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,请你根据图中的信息,若小明把50个纸杯整齐叠放在一起时,它的高度约是 56 cm.
【解答】解:设每两个纸杯叠放在一起比单独的一个纸杯增高x cm,单独一个纸杯的高度为y cm,
由题意得,
解得,
则n个纸杯叠放在一起时的高度为:(n﹣1)x+y=n﹣1+7=(n+6)cm,
当n=50时,其高度为:50+6=56(cm).
故答案为:56.
15.(2024秋 大名县期末)如图,三角形OAB绕点O逆时针旋转75°到三角形OCD的位置,已知∠AOB=45°,则∠AOD= 30° .
【解答】解:∵三角形OAB绕点O逆时针旋转75°到三角形OCD的位置,∠AOB=45°,
∴∠AOC=75°,∠COD=∠AOB=45°,
∴∠AOD=∠AOC﹣∠COD=75°﹣45°=30°,
故答案为:30°.
16.(2024春 金华期末)若关于x,y的二元一次方程mx+ny=3有两个解和,则m+n的值为 6 .
【解答】解:把和代入方程mx+ny=3得:,
①×2得:4m﹣2n=6③,
②+③得:m=3,
把m=3代入①得:n=3,
∴m+n=3+3=6,
故答案为:6.
三.解答题(共8小题)
17.(2024春 岳麓区校级期末)解不等式组:.
【解答】解:,
解①,得x;
解②,得x≤1.
∴原不等式组的解集为x≤1.
18.(2024秋 中牟县期末)解方程组:.
【解答】解:,
①×3+②×2,得13x=65,
解得x=5,
把x=5代入①,得y=2,
故方程组的解为.
19.(2024秋 平果市期末)如图,从①∠1+∠2=180°,②∠3=∠A,③∠B=∠C,三个条件中选出两个作为题设,另一个作为结论可以组成3个命题.从中选择一个真命题,写出已知求证,并证明.
如图,已知 ①② ,求证: ③ .(填“①”,“②”,“③”)
证明:
【解答】答案一:已知①②,求证:③,
证明:∵∠1+∠2=180°,
∴AD∥EF,
∴∠3=∠D,
∵∠3=∠A,
∴∠A=∠D,
∴AB∥CD,
∴∠B=∠C;
答案二:如图,已知①③,求证:②,
证明:∵∠1+∠2=180°,
∴AD∥EF,
∴∠3=∠D,
∵∠B=∠C,
∴AB∥CD,
∴∠A=∠D,
∴∠3=∠A;
答案三:如图,已知②③,求证:①.
证明:∵∠B=∠C,
∴AB∥CD,
∴∠A=∠D,
∵∠3=∠A,
∴∠3=∠D,
∴AD∥EF,
∴∠1+∠2=180°.
20.(2024秋 大东区期末)某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸箱、横式纸箱各加工多少个,恰好能将购进的纸板全部用完?
【解答】解:设加工竖式纸箱x个,加工横式纸箱y个,
根据题意得:,
解得:.
答:加工竖式纸箱200个,加工横式纸箱400个,恰好能将购进的纸板全部用完.
21.(2024秋 宿迁期末)如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.
【解答】解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ,
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y,
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°,
∴x=20°,
∴∠PAQ=20°;
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12,
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,
即CQ+BQ+2PQ=12,
BC+2PQ=12,
∵BC=8,
∴PQ=2.
22.(2024秋 凤阳县期末)新新商场第1次用39万元购进A、B两种商品.销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量).
商品 价格 A B
进价(元/件) 1200 1000
售价(元/件) 1350 1200
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于36000元,则B种商品是打几折销售的?
【解答】解:(1)设该商场第1次购进A商品x件,购进B商品y件,
依题意,得:,
解得:.
答:该商场第1次购进A商品200件,B商品150件.
(2)设B种商品是打m折销售,
依题意,得:(1350﹣1200)×200+(12001000)×150×2=36000,
解得:m=8.5.
答:B种商品是打8.5折销售的.
23.(2024春 榕城区期末)如图,A,B,C三点均在10×10的正方形网格格点上(图中网格线的交点就是格点).
(1)画出将△ABC向右平移4格,再向下平移4格后的△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转180°后的△A2B2C;
(3)在(1)和(2)的条件下,四边形A1B1A2B2是否为中心对称图形?若是,请在图中标出它的对称中心P;若不是,请用所学知识简要说明理由.
【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C即为所求;
(3)四边形A1B1A2B2是中心对称图形,对称中心P如图所示.
24.(2024秋 包头期末)乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片:A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法表示图2大正方形的面积:
方法1: (a+b)2 ,
方法2: a2+b2+2ab ;
(2)观察图2,请你写出三个代数式(a+b)2,a2+b2,ab之间的数量关系: (a+b)2=a2+b2+2ab ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知a+b=7,a2+b2=33,求ab的值;
②已知(2023﹣a)2+(a﹣2021)2=8,求(2023﹣a)(a﹣2021)的值.
【解答】解:(1)(a+b)2,a2+b2+2ab;
(2)(a+b)2=a2+b2+2ab;
(3)①∵a+b=7,a2+b2=33,且 (a+b)2=a2+b2+2ab,
∴49=33+2ab,
解得:ab=8;
②设2023﹣a=m,a﹣2021=n,可得 m2+n2=8,m+n=2023﹣a+a﹣2021=2,
∴(m+n)2=m2+n2+2mn,即4=8+2mn,
解得:mn=﹣2,
则(2023﹣a)(a﹣2021)的值为﹣2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2024秋 临漳县期末)下列语句中,不是命题的是( )
A.两点确定一条直线 B.垂线段最短
C.同位角相等 D.作角A的平分线
2.(2024春 田家庵区校级期末)已知x>y,下列不等式一定成立的是( )
A.x﹣6<y﹣6 B.2x<2y C.﹣2x>﹣2y D.2x+1>2y+1
3.(2024秋 广饶县期末)《国家宝藏》节目立足于中华文化宝库资源.通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是( )
A. B.
C. D.
4.(2024秋 临漳县期末)解关于x,y的二元一次方程组,将①代入②,消去y后所得到的方程是( )
A.3x+4x﹣3=8 B.3x+4x+3=8 C.3x+4x﹣6=8 D.3x+4x+6=8
5.(2023春 埇桥区校级期末)下列运算中正确的是( )
A.b2 b3=b6 B.(2x+y)2=4x2+y2
C.(﹣3x2y)3=﹣27x6y3 D.x+x=x2
6.(2024春 沙河市期末)解不等式时,去分母后结果正确的为( )
A.2(x+2)>1﹣3(x﹣3) B.2x+4>6﹣3x﹣9
C.2x+4>6﹣3x+3 D.2(x+2)>6﹣3(x﹣3)
7.(2024秋 深圳期末)《四元玉鉴》是一部成就辉煌的数学名著,在中国古代数学史上有着重要地位.其中有一个“酒分醇醨”问题:务中听得语吟吟,亩道醇醨酒二盆.醇酒一升醉三客,醨酒三升醉一人.共通饮了一斗七,一十九客醉醺醺.欲问高明能算士,几何醨酒几多醇?其大意为:有好酒和薄酒分别装在瓶中,好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,试问好酒、薄酒各有多少升?若设好酒有x升,薄酒有y升,根据题意列方程组为( )
A. B.
C. D.
8.(2024秋 雁江区校级期末)从边长为a的大正方形纸板正中央挖去一个边长为b的小正方形后,将其裁成四个大小和形状完全相同的四边形(如图1),然后拼成一个平行四边形(如图2),那么通过计算两个图形阴影部分的面积,可以验证成立的等式为( )
A.a2﹣b2=(a﹣b)2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
二.填空题(共8小题)
9.(2023春 石狮市期末)已知a>b,则﹣2a ﹣2b(填“>”、“<”或“=”号).
10.(2023春 垦利区期末)不等式组的解集为 .
11.(2024春 南宁期末)已知x,y满足方程组,则x﹣y的值为 .
12.(2022春 高新区校级期末)如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一次运算.若运算进行了3次才停止,则x的取值范围是 .
13.(2024秋 榆阳区期末)说明命题“若a>b,则ac>bc”的假命题的一个反例的c的值可以是 .
14.(2024秋 浦东新区期末)小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,请你根据图中的信息,若小明把50个纸杯整齐叠放在一起时,它的高度约是 cm.
15.(2024秋 大名县期末)如图,三角形OAB绕点O逆时针旋转75°到三角形OCD的位置,已知∠AOB=45°,则∠AOD= .
16.(2024春 金华期末)若关于x,y的二元一次方程mx+ny=3有两个解和,则m+n的值为 .
三.解答题(共8小题)
17.(2024春 岳麓区校级期末)解不等式组:.
18.(2024秋 中牟县期末)解方程组:.
19.(2024秋 平果市期末)如图,从①∠1+∠2=180°,②∠3=∠A,③∠B=∠C,三个条件中选出两个作为题设,另一个作为结论可以组成3个命题.从中选择一个真命题,写出已知求证,并证明.
如图,已知 ,求证: .(填“①”,“②”,“③”)
证明:
20.(2024秋 大东区期末)某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸箱、横式纸箱各加工多少个,恰好能将购进的纸板全部用完?
21.(2024秋 宿迁期末)如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.
22.(2024秋 凤阳县期末)新新商场第1次用39万元购进A、B两种商品.销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量).
商品 价格 A B
进价(元/件) 1200 1000
售价(元/件) 1350 1200
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于36000元,则B种商品是打几折销售的?
23.(2024春 榕城区期末)如图,A,B,C三点均在10×10的正方形网格格点上(图中网格线的交点就是格点).
(1)画出将△ABC向右平移4格,再向下平移4格后的△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转180°后的△A2B2C;
(3)在(1)和(2)的条件下,四边形A1B1A2B2是否为中心对称图形?若是,请在图中标出它的对称中心P;若不是,请用所学知识简要说明理由.
24.(2024秋 包头期末)乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片:A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法表示图2大正方形的面积:
方法1: ,
方法2: ;
(2)观察图2,请你写出三个代数式(a+b)2,a2+b2,ab之间的数量关系: ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知a+b=7,a2+b2=33,求ab的值;
②已知(2023﹣a)2+(a﹣2021)2=8,求(2023﹣a)(a﹣2021)的值.
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D D B C C D A D
一.选择题(共8小题)
1.(2024秋 临漳县期末)下列语句中,不是命题的是( )
A.两点确定一条直线 B.垂线段最短
C.同位角相等 D.作角A的平分线
【解答】解:两点确定一条直线,垂线段最短,同位角相等都是命题,而作角A的平分线为描述性语言,它不是命题.
故选:D.
2.(2024春 田家庵区校级期末)已知x>y,下列不等式一定成立的是( )
A.x﹣6<y﹣6 B.2x<2y C.﹣2x>﹣2y D.2x+1>2y+1
【解答】解:A、∵x>y,∴x﹣6>y﹣6,原变形错误,不符合题意;
B、∵x>y,∴2x>2y,原变形错误,不符合题意;
C、∵x>y,∴﹣x<﹣y,∴﹣2x<﹣2y,原变形错误,不符合题意
D、∵x>y,∴2x>2y,∴2x+1>2y+1,正确,符合题意.
故选:D.
3.(2024秋 广饶县期末)《国家宝藏》节目立足于中华文化宝库资源.通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、不是轴对称图形,故此选项不合题意;
B、是轴对称图形,故此选项符合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意;
故选:B.
4.(2024秋 临漳县期末)解关于x,y的二元一次方程组,将①代入②,消去y后所得到的方程是( )
A.3x+4x﹣3=8 B.3x+4x+3=8 C.3x+4x﹣6=8 D.3x+4x+6=8
【解答】解:,
将①代入②,消去y后所得到的方程是3x+2(2x﹣3)=8,
去括号,得3x+4x﹣6=8.
故选:C.
5.(2023春 埇桥区校级期末)下列运算中正确的是( )
A.b2 b3=b6 B.(2x+y)2=4x2+y2
C.(﹣3x2y)3=﹣27x6y3 D.x+x=x2
【解答】解:A、b2 b3=b5,不符合题意;
B、(2x+y)2=4x2+4xy+y2,不符合题意;
C、(﹣3x2y)3=﹣27x6y3,符合题意;
D、x+x=2x,不符合题意.
故选:C.
6.(2024春 沙河市期末)解不等式时,去分母后结果正确的为( )
A.2(x+2)>1﹣3(x﹣3) B.2x+4>6﹣3x﹣9
C.2x+4>6﹣3x+3 D.2(x+2)>6﹣3(x﹣3)
【解答】解:去分母得2(x+2)>6﹣3(x﹣3).
故选:D.
7.(2024秋 深圳期末)《四元玉鉴》是一部成就辉煌的数学名著,在中国古代数学史上有着重要地位.其中有一个“酒分醇醨”问题:务中听得语吟吟,亩道醇醨酒二盆.醇酒一升醉三客,醨酒三升醉一人.共通饮了一斗七,一十九客醉醺醺.欲问高明能算士,几何醨酒几多醇?其大意为:有好酒和薄酒分别装在瓶中,好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,试问好酒、薄酒各有多少升?若设好酒有x升,薄酒有y升,根据题意列方程组为( )
A. B.
C. D.
【解答】解:∵好酒和薄酒一共饮了17升,
∴x+y=17;
∵好酒1升醉了3位客人,薄酒3升醉了1位客人,且共醉了19位客人,
∴3xy=19.
∴根据题意可列方程组.
故选:A.
8.(2024秋 雁江区校级期末)从边长为a的大正方形纸板正中央挖去一个边长为b的小正方形后,将其裁成四个大小和形状完全相同的四边形(如图1),然后拼成一个平行四边形(如图2),那么通过计算两个图形阴影部分的面积,可以验证成立的等式为( )
A.a2﹣b2=(a﹣b)2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
【解答】解:图1中阴影部分的面积为:a2﹣b2,图2中阴影部分的面积为:(a+b)(a﹣b),
∵两图中阴影部分的面积相等,
∴a2﹣b2=(a+b)(a﹣b),
∴可以验证成立的公式为a2﹣b2=(a+b)(a﹣b),
故选:D.
二.填空题(共8小题)
9.(2023春 石狮市期末)已知a>b,则﹣2a < ﹣2b(填“>”、“<”或“=”号).
【解答】解:∵a>b,
∴﹣2a<﹣2b,
故答案为:<.
10.(2023春 垦利区期末)不等式组的解集为 ﹣3<x≤1 .
【解答】解:由x+2≤3得:x≤1,
由1+x>﹣2得:x>﹣3,
则不等式组的解集为﹣3<x≤1,
故答案为:﹣3<x≤1.
11.(2024春 南宁期末)已知x,y满足方程组,则x﹣y的值为 ﹣1 .
【解答】解:,
①﹣②得:x﹣y=﹣1,
故答案为:﹣1
12.(2022春 高新区校级期末)如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一次运算.若运算进行了3次才停止,则x的取值范围是 2<x≤4 .
【解答】解:依题意得:,
解得:2<x≤4,
故答案为:2<x≤4.
13.(2024秋 榆阳区期末)说明命题“若a>b,则ac>bc”的假命题的一个反例的c的值可以是 0 .
【解答】解:若a>b,当c=0时ac=bc=0,
故答案为:0(答案不唯一).
14.(2024秋 浦东新区期末)小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,请你根据图中的信息,若小明把50个纸杯整齐叠放在一起时,它的高度约是 56 cm.
【解答】解:设每两个纸杯叠放在一起比单独的一个纸杯增高x cm,单独一个纸杯的高度为y cm,
由题意得,
解得,
则n个纸杯叠放在一起时的高度为:(n﹣1)x+y=n﹣1+7=(n+6)cm,
当n=50时,其高度为:50+6=56(cm).
故答案为:56.
15.(2024秋 大名县期末)如图,三角形OAB绕点O逆时针旋转75°到三角形OCD的位置,已知∠AOB=45°,则∠AOD= 30° .
【解答】解:∵三角形OAB绕点O逆时针旋转75°到三角形OCD的位置,∠AOB=45°,
∴∠AOC=75°,∠COD=∠AOB=45°,
∴∠AOD=∠AOC﹣∠COD=75°﹣45°=30°,
故答案为:30°.
16.(2024春 金华期末)若关于x,y的二元一次方程mx+ny=3有两个解和,则m+n的值为 6 .
【解答】解:把和代入方程mx+ny=3得:,
①×2得:4m﹣2n=6③,
②+③得:m=3,
把m=3代入①得:n=3,
∴m+n=3+3=6,
故答案为:6.
三.解答题(共8小题)
17.(2024春 岳麓区校级期末)解不等式组:.
【解答】解:,
解①,得x;
解②,得x≤1.
∴原不等式组的解集为x≤1.
18.(2024秋 中牟县期末)解方程组:.
【解答】解:,
①×3+②×2,得13x=65,
解得x=5,
把x=5代入①,得y=2,
故方程组的解为.
19.(2024秋 平果市期末)如图,从①∠1+∠2=180°,②∠3=∠A,③∠B=∠C,三个条件中选出两个作为题设,另一个作为结论可以组成3个命题.从中选择一个真命题,写出已知求证,并证明.
如图,已知 ①② ,求证: ③ .(填“①”,“②”,“③”)
证明:
【解答】答案一:已知①②,求证:③,
证明:∵∠1+∠2=180°,
∴AD∥EF,
∴∠3=∠D,
∵∠3=∠A,
∴∠A=∠D,
∴AB∥CD,
∴∠B=∠C;
答案二:如图,已知①③,求证:②,
证明:∵∠1+∠2=180°,
∴AD∥EF,
∴∠3=∠D,
∵∠B=∠C,
∴AB∥CD,
∴∠A=∠D,
∴∠3=∠A;
答案三:如图,已知②③,求证:①.
证明:∵∠B=∠C,
∴AB∥CD,
∴∠A=∠D,
∵∠3=∠A,
∴∠3=∠D,
∴AD∥EF,
∴∠1+∠2=180°.
20.(2024秋 大东区期末)某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸箱、横式纸箱各加工多少个,恰好能将购进的纸板全部用完?
【解答】解:设加工竖式纸箱x个,加工横式纸箱y个,
根据题意得:,
解得:.
答:加工竖式纸箱200个,加工横式纸箱400个,恰好能将购进的纸板全部用完.
21.(2024秋 宿迁期末)如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.
【解答】解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ,
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y,
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°,
∴x=20°,
∴∠PAQ=20°;
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12,
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,
即CQ+BQ+2PQ=12,
BC+2PQ=12,
∵BC=8,
∴PQ=2.
22.(2024秋 凤阳县期末)新新商场第1次用39万元购进A、B两种商品.销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量).
商品 价格 A B
进价(元/件) 1200 1000
售价(元/件) 1350 1200
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于36000元,则B种商品是打几折销售的?
【解答】解:(1)设该商场第1次购进A商品x件,购进B商品y件,
依题意,得:,
解得:.
答:该商场第1次购进A商品200件,B商品150件.
(2)设B种商品是打m折销售,
依题意,得:(1350﹣1200)×200+(12001000)×150×2=36000,
解得:m=8.5.
答:B种商品是打8.5折销售的.
23.(2024春 榕城区期末)如图,A,B,C三点均在10×10的正方形网格格点上(图中网格线的交点就是格点).
(1)画出将△ABC向右平移4格,再向下平移4格后的△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转180°后的△A2B2C;
(3)在(1)和(2)的条件下,四边形A1B1A2B2是否为中心对称图形?若是,请在图中标出它的对称中心P;若不是,请用所学知识简要说明理由.
【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C即为所求;
(3)四边形A1B1A2B2是中心对称图形,对称中心P如图所示.
24.(2024秋 包头期末)乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片:A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法表示图2大正方形的面积:
方法1: (a+b)2 ,
方法2: a2+b2+2ab ;
(2)观察图2,请你写出三个代数式(a+b)2,a2+b2,ab之间的数量关系: (a+b)2=a2+b2+2ab ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知a+b=7,a2+b2=33,求ab的值;
②已知(2023﹣a)2+(a﹣2021)2=8,求(2023﹣a)(a﹣2021)的值.
【解答】解:(1)(a+b)2,a2+b2+2ab;
(2)(a+b)2=a2+b2+2ab;
(3)①∵a+b=7,a2+b2=33,且 (a+b)2=a2+b2+2ab,
∴49=33+2ab,
解得:ab=8;
②设2023﹣a=m,a﹣2021=n,可得 m2+n2=8,m+n=2023﹣a+a﹣2021=2,
∴(m+n)2=m2+n2+2mn,即4=8+2mn,
解得:mn=﹣2,
则(2023﹣a)(a﹣2021)的值为﹣2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
