数学:23.1图形的旋转课件(人教新课标九年级上)
文档属性
| 名称 | 数学:23.1图形的旋转课件(人教新课标九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 689.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-15 00:00:00 | ||
图片预览





文档简介
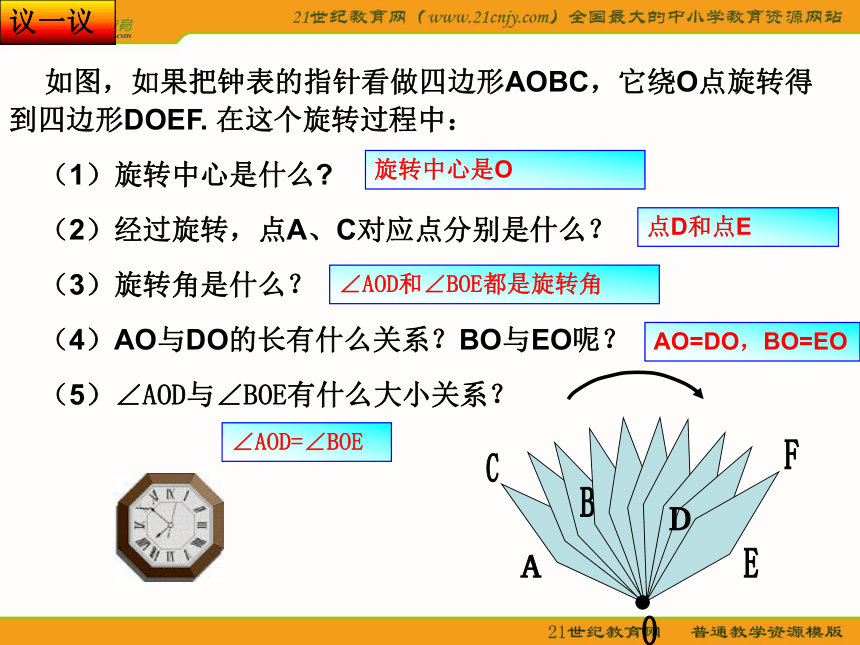
课件21张PPT。观 察归纳定义 把一个图形绕着某一定点O转动一个角度的图形变换叫做旋转.这个定点O叫旋转中心,转动的角叫做旋转角. 如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点. 动态演示OP′P 如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、C对应点分别是什么?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
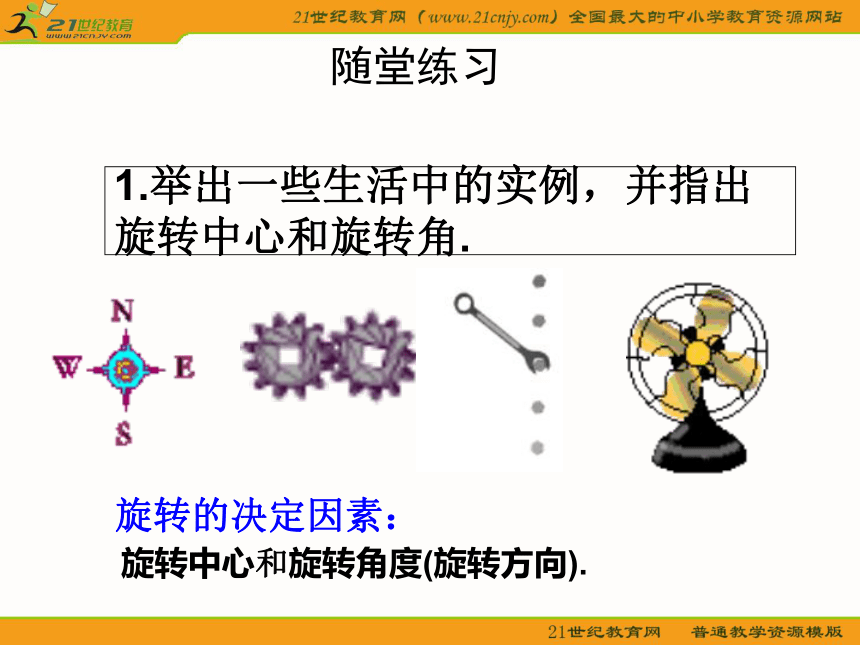
(5)∠AOD与∠BOE有什么大小关系?议一议旋转中心是O点D和点EAO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEF1.举出一些生活中的实例,并指出旋转中心和旋转角. 旋转的决定因素:
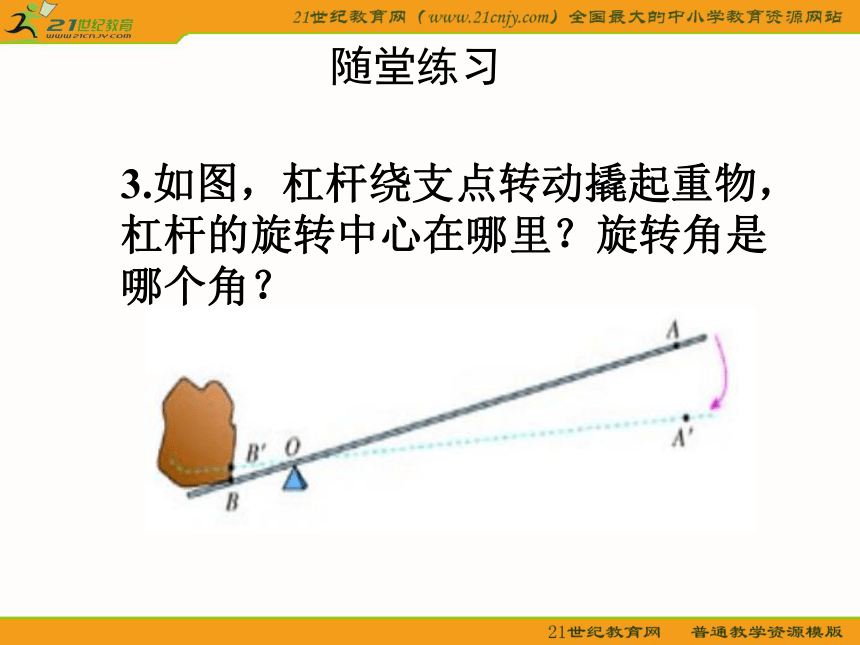
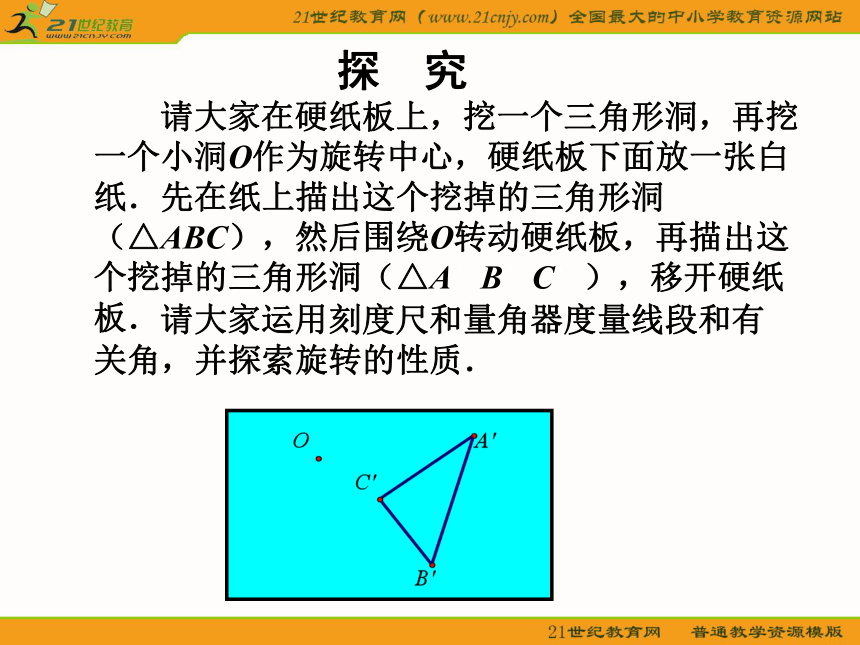
旋转中心和旋转角度(旋转方向).随堂练习随堂练习2.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?随堂练习3.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?探 究 请大家在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形洞(△ABC),然后围绕O转动硬纸板,再描出这个挖掉的三角形洞(△A′B′C′),移开硬纸板. 请大家运用刻度尺和量角器度量线段和有关角,并探索旋转的性质.3.◆旋转前、后的图形全等. 1.◆对应点到旋转中心的距离相等. 2.◆每一对对应点与旋转中心所连线段的夹 角等于旋转角. 旋转的基本性质 ◆图形的旋转是由旋转中心和旋转的角
度决定. 发 现例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.例题讲解 设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE . 解:因为点A是旋转中心,所以它的对应点是它本身. 在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合. 因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.例题解答例2.已知△ABC,作下列旋转
(1)以点B为中心,把这个三角形旋转30°
(2)在三角形外任意取一点 为中心。把这个三角形旋转90°1.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得的, ①请你在图中用字母O标注出这一点; ②每次旋转了_______度;
③一共旋转了_______次.随堂练习随堂练习60°52.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?随堂练习3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有 个. 随堂练习●14.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.随堂练习P●P/●5.如图,用左面的三角形经过怎样旋转,可以得到右面的图形.6.找出图中扳手拧螺母时的旋转中心和旋转角.随堂练习 答:三角形绕着点O旋转1200,连续旋转两次,可以得到右边的图形O●答:螺母的中心O就是旋转中心,∠AOA/为旋转角 请设计一个绕一点旋转60°后能与自身重合的图形.动手操作 对比平移、轴对称两种变换,旋转变换与另两种变换有哪些共性与区别?小 结课堂小结平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
作业:第59页,60页 习题 1 . .3. 4 .5 (作业纸)
2(书)再见
(1)旋转中心是什么?
(2)经过旋转,点A、C对应点分别是什么?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?议一议旋转中心是O点D和点EAO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEF1.举出一些生活中的实例,并指出旋转中心和旋转角. 旋转的决定因素:
旋转中心和旋转角度(旋转方向).随堂练习随堂练习2.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?随堂练习3.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?探 究 请大家在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形洞(△ABC),然后围绕O转动硬纸板,再描出这个挖掉的三角形洞(△A′B′C′),移开硬纸板. 请大家运用刻度尺和量角器度量线段和有关角,并探索旋转的性质.3.◆旋转前、后的图形全等. 1.◆对应点到旋转中心的距离相等. 2.◆每一对对应点与旋转中心所连线段的夹 角等于旋转角. 旋转的基本性质 ◆图形的旋转是由旋转中心和旋转的角
度决定. 发 现例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.例题讲解 设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE . 解:因为点A是旋转中心,所以它的对应点是它本身. 在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合. 因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.例题解答例2.已知△ABC,作下列旋转
(1)以点B为中心,把这个三角形旋转30°
(2)在三角形外任意取一点 为中心。把这个三角形旋转90°1.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得的, ①请你在图中用字母O标注出这一点; ②每次旋转了_______度;
③一共旋转了_______次.随堂练习随堂练习60°52.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?随堂练习3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有 个. 随堂练习●14.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.随堂练习P●P/●5.如图,用左面的三角形经过怎样旋转,可以得到右面的图形.6.找出图中扳手拧螺母时的旋转中心和旋转角.随堂练习 答:三角形绕着点O旋转1200,连续旋转两次,可以得到右边的图形O●答:螺母的中心O就是旋转中心,∠AOA/为旋转角 请设计一个绕一点旋转60°后能与自身重合的图形.动手操作 对比平移、轴对称两种变换,旋转变换与另两种变换有哪些共性与区别?小 结课堂小结平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
作业:第59页,60页 习题 1 . .3. 4 .5 (作业纸)
2(书)再见
同课章节目录
