19.2.3 一次函数与方程、不等式 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 195.8KB | ||
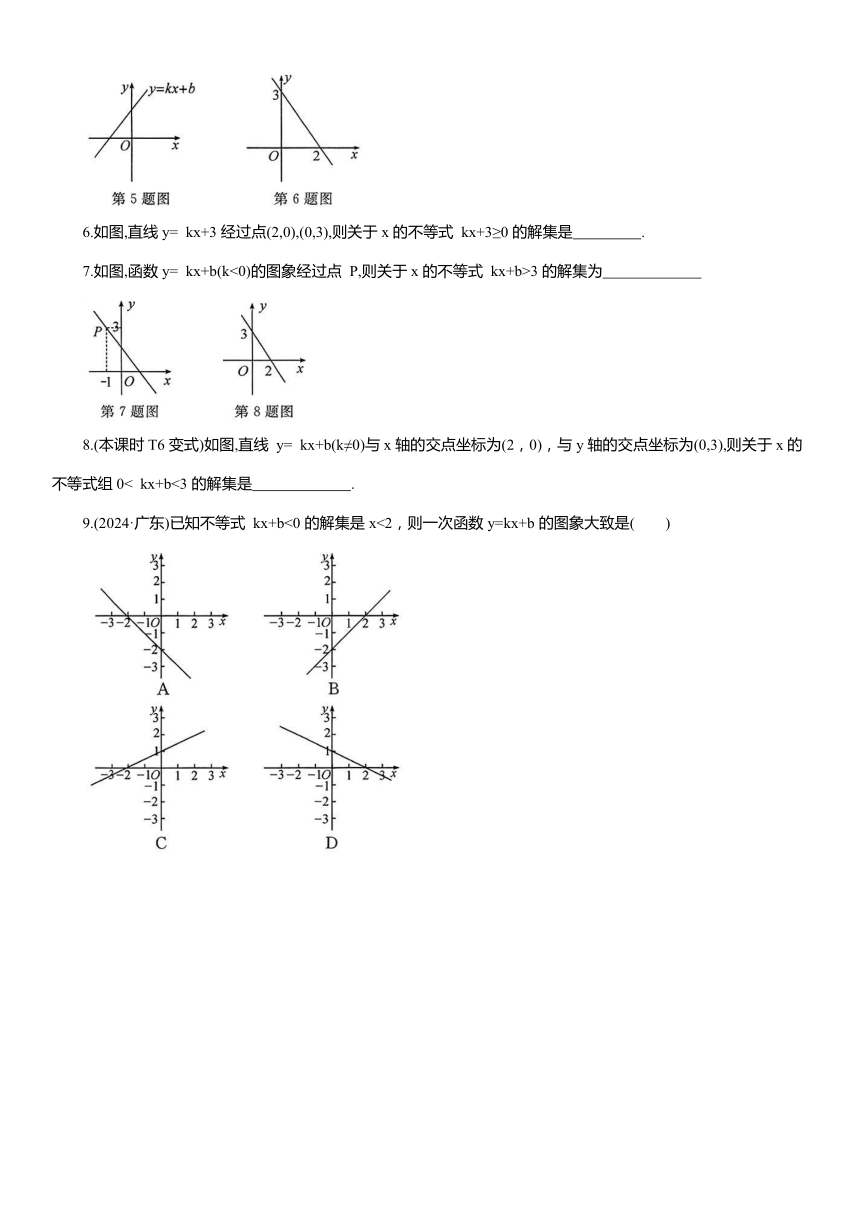
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 08:40:26 | ||
图片预览



文档简介
19.2.3 一次函数与方程、不等式
第1课时 一次函数与一元一次方程、不等式
A 基础题
知识点1 一次函数与一元一次方程
1.(1)一元一次方程—2x+4=0的解是 .
(2)函数y=-2x+4,当x= 时,函数值y=0.
(3)直线 y=--2x+4 与x轴的交点坐标是
(4)由上述问题可知,一元一次方程 ax+b=0的解就是一次函数y=ax+b当y=0时所对应的 的值;从图象上看,就是一次函数y=ax+b的图象与 轴交点的 .
2.已知方程 ax+b=0的解为 则一次函数y=ax+b的图象与x轴交点的横坐标为( )
A.3 C. --2
3.若一次函数y= ax+b(a,b为常数且a≠0)中x与y的部分对应值如下表,则方程 ax+b=0的解是 ( )
x 0 1 2 3
y 6 4 2 0
A. x=1 B. x=--1
C. x=2 D. x=3
4.已知一次函数y=kx+b的图象如图所示,利用图象解决下列问题.
(1)关于x的方程 kx+b=0的解是 .
(2)关于x的方程 kx+b=2 的解是 .
(3)关于x的方程 kx+b=4 的解是 .
知识点2 一次函数与一元一次不等式
5.已知一次函数y=kx+b的图象如图所示.
(1)关于x的不等式 kx+b>0的解集就是直线 y= kx+b在x 轴 (填“上方”或“下方”)部分对应的x的取值范围.
(2)关于x的不等式 kx+b<0的解集就是直线y= kx+b在x 轴 (填“上方”或“下方”)部分对应的x的取值范围.
6.如图,直线y= kx+3经过点(2,0),(0,3),则关于x的不等式 kx+3≥0的解集是 .
7.如图,函数y= kx+b(k<0)的图象经过点 P,则关于x的不等式 kx+b>3的解集为
8.(本课时T6变式)如图,直线 y= kx+b(k≠0)与x轴的交点坐标为(2,0),与y轴的交点坐标为(0,3),则关于x的不等式组0< kx+b<3的解集是 .
9.(2024·广东)已知不等式 kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是( )
B 中档题
10.(2024·扬州改编)如图,一次函数y= kx+b(k≠0)的图象分别与x轴、y轴交于 A,B两点.若 则关于x的方程 kx+b=0的解为 .
11.已知y= kx+2,当x<--1时,其图象在x轴下方;当x>--1时,其图象在x轴上方,则k的值为 ( )
A. -2 B.2 C. -3 D.3
12.如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x 的增大而减小;②k>0,b<0;③关于x的方程kx+b=0的解为x=--2;④当x>--2时,y>0.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
13.如图,一次函数y= kx+b(k>0)的图象过点(--1,0),则关于x的不等式k(x--1)+b>0的解集是 ( )
A. x>-2 B. x>-1
C. x>0 D. x>1
14.在学习一元一次不等式与一次函数中,小明在同一个平面直角坐标系中分别作出了一次函数 和y= kx+b的图象,分别与x轴交于点A,B,两直线相交于点 C.已知点A(--1,0),B(2,0),观察图象并回答下列问题:
(1)关于x的方程 的解是 ,关于x的不等式 kx+b<0的解集是 .
(2)求关于x的不等式组 的解集.
C 综合题
15.学习函数的时候,我们通过列表、描点和连线的步骤画出函数的图象,进而研究函数的性质.请根据学习“一次函数”时积累的经验和方法研究函数y=--|x+1|+2的图象和性质,并解决问题.
(1)①列表填空:
x … -3 -2 0 1 ……
y … 1 2 0 ……
②在平面直角坐标系中作出函数 y=-|x+1|+2的图象.
(2)观察函数图象,写出关于这个函数的两条性质:
(3)进一步探究函数图象发现:
①方程--|x+1|+2=0有 个解.
②若关于x的方程--|x+1|+2=a无解,则a的取值范围是 .
一次函数与二元一次方程组
A基础题
知识点1 一次函数与二元一次方程(组)的关系
1.(1)方程2x--y=2的解有 个.
(2)以方程2x--y=2的解为坐标的点组成的图象与一次函数 的图象相同.
(3)以下图象中,直线上每个点的坐标都是二元一次方程2x--y=2的解的是 ( )
2.如图,直线y=2x+b与直线y=-3x+6相交于点 A,则关于x,y的 二 元 一 次 方 程 组 的解为 .
3.已知二元一次方程组 的 解 是 则在同一平面直角坐标系中,直线 y=x--5 与直线y=--x+1的交点坐标为
4.如图,直线 l 的函数解析式为 y=2x--2,直线 l 与x轴交于点 D.直线l :y= kx+b与x轴交于点A,且经过点 B(3,1),直线 l ,l 交于点C(m,2).
(1)求点 D,C的坐标.
(2)直线 l 的函数解析式为 .
(3)关于 x, y 的 二 元 一 次 方 程 组 的解为 .
知识点2 利用二元一次方程组求两个一次函数图象的交点坐标
5.(教材习题变式)当函数 与y=-x-5的函数值相等时,自变量x的值是 .
6.已知函数y=2x--1与y=3x+2的图象相交于点 P,则点 P 的坐标是 .
知识点3 由两个一次函数图象的交点求不等
式的解集
7.如图,已知函数y=2x+b与函数y= kx---3的图象交于点 P,则不等式 kx--3>2x+b的解集是 ( )
A. x>-6 B. x<-6
C. x>2 D. x<2
8.如图,已知一次函数 的图象与正比例函数 的图象的交点A 的纵坐标是4,且与x轴的交点B 的横坐标是-3.
(1)这个一次函数的解析式为 .
(2)当 时,x的取值范围是
B 中档题
9.如图,直线y=2x+6与直线y= kx+b(k,b为常数,k≠0)相交于点 A(m,4),则关于x的不等式2x+6< kx+b的解集为( )
A. x>-1
B. x<-2
C. x<-1
D. x>-2
10.如图,已知正比例函数 与一次函数 的图象相交于点 P,则以下结论:①a>0;②2a+b=1;③当x<0时,y >0;④当x<-2时, 其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
11.若直线y=2x+b经过直线y=x--2与直线y=3x+4的交点,则b的值为 .
12.如图,直线 y= kx+b经过A(--2,--1),B(-3,0)两点,则不等式组 的解集为 .
13.(2023·北京)在平面直角坐标系xOy中,函数y= kx+b(k≠0)的图象经过点 A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.
(1)求该函数的解析式及点 C 的坐标.
(2)当x<3时,对于x的每一个值,函数y= 的值大于函数y= kx+b(k≠0)的值且小于4,直接写出n的值.
C综合题
14. A,B两地相距100 千米,甲、乙两人骑车分别从 A,B两地相向而行,图中 l 和l 分别表示他们各自到 A 地的距离 y(千米)与时间x(时)的关系.根据图中提供的信息,解答下列问题:
(1)图中 表示甲到 A 地的距离与时间的关系.
(2)甲、乙两人的速度分别是多少
(3)求点 P 的坐标,并解释点 P 的实际意义.
(4)甲出发 小时后,两人相距30千米.
19.2.3 一次函数与方程、不等式
第1课时 一次函数与一元一次方程、不等式
1.(1)x=2 (2)2 (3)(2,0) (4)x x 横坐标 2. D 3 . A
4.(1)x=2 (2)x=1 (3)x=0 5.(1)上方 (2)下方 6. x≤2
7. x<-1 8.014.解:(1)x=-1 x>2 (2)根据图象可得,关于x的不等式组 的解集为-115.解:(1)①0 1②函数y=-|x+1|+2的图象略.(2)①函数的最大值是2[或者函数图象最高点的坐标是(-1,2)];②函数图象关于直线x=-1对称;③当x>-1时,y随x的增大而减小(或者当x<-1时,y随x的增大而增大)(答案不唯一) (3)①2 ②a>2
第2课时 一次函数与二元一次方程组
1.(1)无数(2)y=2x-2 (3)B 3.(3, -2)
4.解:(1)∵点D为直线l :y=2x-2与x轴的交点,∴将 y=0代入y=2x-2,得0=2x--2,解得x=1.∴点D的坐标为(1,0).∵点C(m,2)在直线 上,∴2=2m-2,解得m=2.∴点C的坐标为(2,2).(2)y=-x+4
5.-4 6.(-3,-7) 7. D 8 (2)013.解:(1)把点 A(0,1),B(1,2)代入:y= kx+b(k≠0),得 解得该函数的解析式为y=x+1.由题意可知,点 C的纵坐标为4,当y=4时,x+1=4,解得x=3.∴C(3,4).(2)n=2.
14.解:(1)l (2)甲的速度为30千米/时,乙的速度为20千米/时.(3)设l 的解析式为 根据题意,得 解得的解析式为y=30x-30.设l 的解析式为 y= 根据题意,得 解得的解析式为y=-20x+100.联立 解得点P的坐标为(2.6,48),点P 的实际意义为乙出发2.6小时后两人相遇,这时两人距离A地48千米.(4)1或2.2
第1课时 一次函数与一元一次方程、不等式
A 基础题
知识点1 一次函数与一元一次方程
1.(1)一元一次方程—2x+4=0的解是 .
(2)函数y=-2x+4,当x= 时,函数值y=0.
(3)直线 y=--2x+4 与x轴的交点坐标是
(4)由上述问题可知,一元一次方程 ax+b=0的解就是一次函数y=ax+b当y=0时所对应的 的值;从图象上看,就是一次函数y=ax+b的图象与 轴交点的 .
2.已知方程 ax+b=0的解为 则一次函数y=ax+b的图象与x轴交点的横坐标为( )
A.3 C. --2
3.若一次函数y= ax+b(a,b为常数且a≠0)中x与y的部分对应值如下表,则方程 ax+b=0的解是 ( )
x 0 1 2 3
y 6 4 2 0
A. x=1 B. x=--1
C. x=2 D. x=3
4.已知一次函数y=kx+b的图象如图所示,利用图象解决下列问题.
(1)关于x的方程 kx+b=0的解是 .
(2)关于x的方程 kx+b=2 的解是 .
(3)关于x的方程 kx+b=4 的解是 .
知识点2 一次函数与一元一次不等式
5.已知一次函数y=kx+b的图象如图所示.
(1)关于x的不等式 kx+b>0的解集就是直线 y= kx+b在x 轴 (填“上方”或“下方”)部分对应的x的取值范围.
(2)关于x的不等式 kx+b<0的解集就是直线y= kx+b在x 轴 (填“上方”或“下方”)部分对应的x的取值范围.
6.如图,直线y= kx+3经过点(2,0),(0,3),则关于x的不等式 kx+3≥0的解集是 .
7.如图,函数y= kx+b(k<0)的图象经过点 P,则关于x的不等式 kx+b>3的解集为
8.(本课时T6变式)如图,直线 y= kx+b(k≠0)与x轴的交点坐标为(2,0),与y轴的交点坐标为(0,3),则关于x的不等式组0< kx+b<3的解集是 .
9.(2024·广东)已知不等式 kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是( )
B 中档题
10.(2024·扬州改编)如图,一次函数y= kx+b(k≠0)的图象分别与x轴、y轴交于 A,B两点.若 则关于x的方程 kx+b=0的解为 .
11.已知y= kx+2,当x<--1时,其图象在x轴下方;当x>--1时,其图象在x轴上方,则k的值为 ( )
A. -2 B.2 C. -3 D.3
12.如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x 的增大而减小;②k>0,b<0;③关于x的方程kx+b=0的解为x=--2;④当x>--2时,y>0.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
13.如图,一次函数y= kx+b(k>0)的图象过点(--1,0),则关于x的不等式k(x--1)+b>0的解集是 ( )
A. x>-2 B. x>-1
C. x>0 D. x>1
14.在学习一元一次不等式与一次函数中,小明在同一个平面直角坐标系中分别作出了一次函数 和y= kx+b的图象,分别与x轴交于点A,B,两直线相交于点 C.已知点A(--1,0),B(2,0),观察图象并回答下列问题:
(1)关于x的方程 的解是 ,关于x的不等式 kx+b<0的解集是 .
(2)求关于x的不等式组 的解集.
C 综合题
15.学习函数的时候,我们通过列表、描点和连线的步骤画出函数的图象,进而研究函数的性质.请根据学习“一次函数”时积累的经验和方法研究函数y=--|x+1|+2的图象和性质,并解决问题.
(1)①列表填空:
x … -3 -2 0 1 ……
y … 1 2 0 ……
②在平面直角坐标系中作出函数 y=-|x+1|+2的图象.
(2)观察函数图象,写出关于这个函数的两条性质:
(3)进一步探究函数图象发现:
①方程--|x+1|+2=0有 个解.
②若关于x的方程--|x+1|+2=a无解,则a的取值范围是 .
一次函数与二元一次方程组
A基础题
知识点1 一次函数与二元一次方程(组)的关系
1.(1)方程2x--y=2的解有 个.
(2)以方程2x--y=2的解为坐标的点组成的图象与一次函数 的图象相同.
(3)以下图象中,直线上每个点的坐标都是二元一次方程2x--y=2的解的是 ( )
2.如图,直线y=2x+b与直线y=-3x+6相交于点 A,则关于x,y的 二 元 一 次 方 程 组 的解为 .
3.已知二元一次方程组 的 解 是 则在同一平面直角坐标系中,直线 y=x--5 与直线y=--x+1的交点坐标为
4.如图,直线 l 的函数解析式为 y=2x--2,直线 l 与x轴交于点 D.直线l :y= kx+b与x轴交于点A,且经过点 B(3,1),直线 l ,l 交于点C(m,2).
(1)求点 D,C的坐标.
(2)直线 l 的函数解析式为 .
(3)关于 x, y 的 二 元 一 次 方 程 组 的解为 .
知识点2 利用二元一次方程组求两个一次函数图象的交点坐标
5.(教材习题变式)当函数 与y=-x-5的函数值相等时,自变量x的值是 .
6.已知函数y=2x--1与y=3x+2的图象相交于点 P,则点 P 的坐标是 .
知识点3 由两个一次函数图象的交点求不等
式的解集
7.如图,已知函数y=2x+b与函数y= kx---3的图象交于点 P,则不等式 kx--3>2x+b的解集是 ( )
A. x>-6 B. x<-6
C. x>2 D. x<2
8.如图,已知一次函数 的图象与正比例函数 的图象的交点A 的纵坐标是4,且与x轴的交点B 的横坐标是-3.
(1)这个一次函数的解析式为 .
(2)当 时,x的取值范围是
B 中档题
9.如图,直线y=2x+6与直线y= kx+b(k,b为常数,k≠0)相交于点 A(m,4),则关于x的不等式2x+6< kx+b的解集为( )
A. x>-1
B. x<-2
C. x<-1
D. x>-2
10.如图,已知正比例函数 与一次函数 的图象相交于点 P,则以下结论:①a>0;②2a+b=1;③当x<0时,y >0;④当x<-2时, 其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
11.若直线y=2x+b经过直线y=x--2与直线y=3x+4的交点,则b的值为 .
12.如图,直线 y= kx+b经过A(--2,--1),B(-3,0)两点,则不等式组 的解集为 .
13.(2023·北京)在平面直角坐标系xOy中,函数y= kx+b(k≠0)的图象经过点 A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.
(1)求该函数的解析式及点 C 的坐标.
(2)当x<3时,对于x的每一个值,函数y= 的值大于函数y= kx+b(k≠0)的值且小于4,直接写出n的值.
C综合题
14. A,B两地相距100 千米,甲、乙两人骑车分别从 A,B两地相向而行,图中 l 和l 分别表示他们各自到 A 地的距离 y(千米)与时间x(时)的关系.根据图中提供的信息,解答下列问题:
(1)图中 表示甲到 A 地的距离与时间的关系.
(2)甲、乙两人的速度分别是多少
(3)求点 P 的坐标,并解释点 P 的实际意义.
(4)甲出发 小时后,两人相距30千米.
19.2.3 一次函数与方程、不等式
第1课时 一次函数与一元一次方程、不等式
1.(1)x=2 (2)2 (3)(2,0) (4)x x 横坐标 2. D 3 . A
4.(1)x=2 (2)x=1 (3)x=0 5.(1)上方 (2)下方 6. x≤2
7. x<-1 8.0
第2课时 一次函数与二元一次方程组
1.(1)无数(2)y=2x-2 (3)B 3.(3, -2)
4.解:(1)∵点D为直线l :y=2x-2与x轴的交点,∴将 y=0代入y=2x-2,得0=2x--2,解得x=1.∴点D的坐标为(1,0).∵点C(m,2)在直线 上,∴2=2m-2,解得m=2.∴点C的坐标为(2,2).(2)y=-x+4
5.-4 6.(-3,-7) 7. D 8 (2)0
14.解:(1)l (2)甲的速度为30千米/时,乙的速度为20千米/时.(3)设l 的解析式为 根据题意,得 解得的解析式为y=30x-30.设l 的解析式为 y= 根据题意,得 解得的解析式为y=-20x+100.联立 解得点P的坐标为(2.6,48),点P 的实际意义为乙出发2.6小时后两人相遇,这时两人距离A地48千米.(4)1或2.2
