平行四边形期末复习(三) 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 平行四边形期末复习(三) 同步练习(含答案)2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览




文档简介
平行四边形期末复习(三)
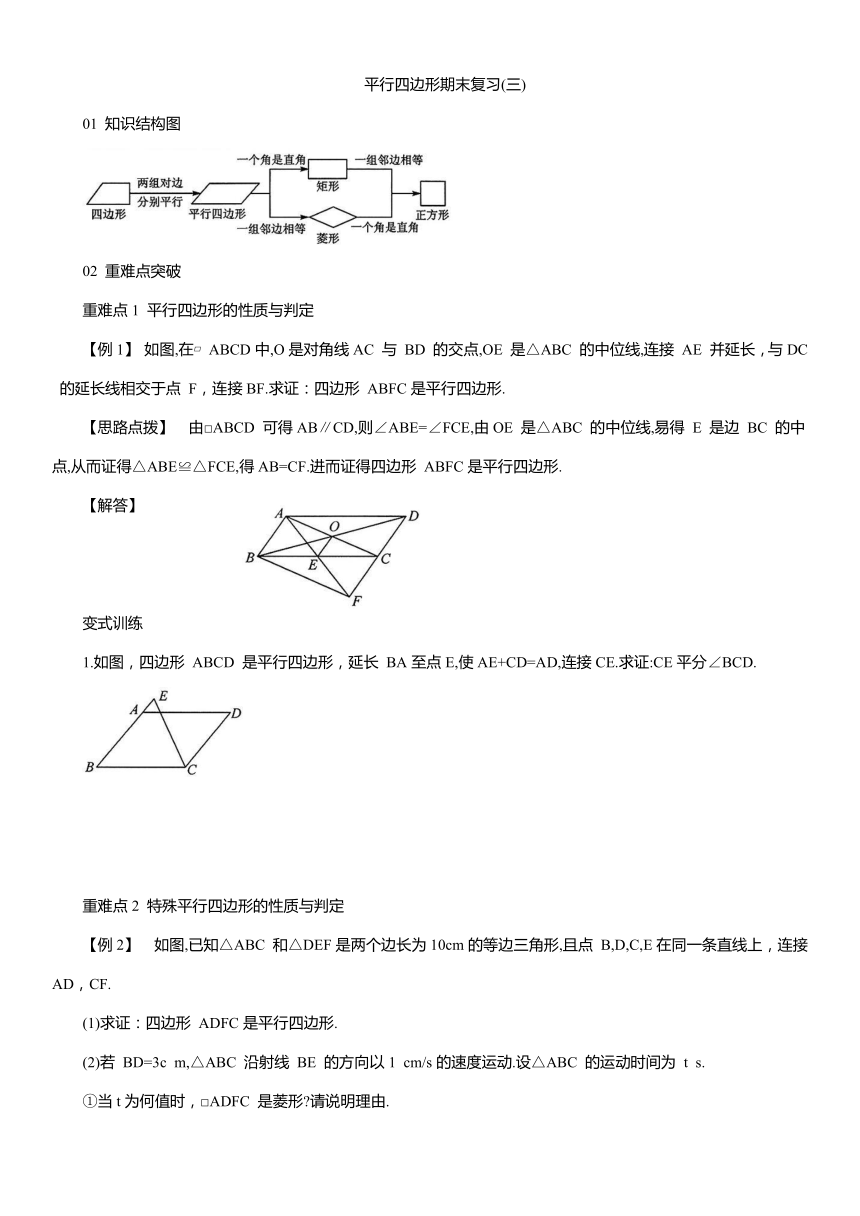
01 知识结构图
02 重难点突破
重难点1 平行四边形的性质与判定
【例1】 如图,在 ABCD中,O是对角线AC 与 BD 的交点,OE 是△ABC 的中位线,连接 AE 并延长,与DC 的延长线相交于点 F,连接BF.求证:四边形 ABFC是平行四边形.
【思路点拨】 由□ABCD 可得AB∥CD,则∠ABE=∠FCE,由OE 是△ABC 的中位线,易得 E 是边 BC 的中点,从而证得△ABE≌△FCE,得AB=CF.进而证得四边形 ABFC是平行四边形.
【解答】
变式训练
1.如图,四边形 ABCD 是平行四边形,延长 BA至点E,使AE+CD=AD,连接CE.求证:CE平分∠BCD.
重难点2 特殊平行四边形的性质与判定
【例2】 如图,已知△ABC 和△DEF是两个边长为10cm的等边三角形,且点 B,D,C,E在同一条直线上,连接AD,CF.
(1)求证:四边形 ADFC是平行四边形.
(2)若 BD=3c m,△ABC 沿射线 BE 的方向以1 cm/s的速度运动.设△ABC 的运动时间为 t s.
①当t为何值时,□ADFC 是菱形 请说明理由.
②□ADFC有可能是矩形吗 若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
【思路点拨】 (1)由△ABC 和△DEF是两个边长为 10 cm 的等边三角形,得AC=DF,∠ACD=∠FDE=60°,从而得 AC∥DF,所以四边形ADFC是平行四边形;(2)①若□ADFC是菱形,则点 B 与点 D 重合,从而得出△ABC沿射线BE 的方向移动的距离,进而求出运动的时间;②若 ADFC是矩形,则∠DAC=90°,从而可推断点 E 与点B 重合,得出△ABC 沿射线BE 的方向移动的距离,进而求出运动的时间及此矩形的面积.
【解答】
变式训练
2.如图,在矩形 ABCD中,E是边BC 上一点,DE平分∠ADC,EF∥DC,交边 AD于点F,连接 BD.
(1)求证:四边形 EFDC是正方形.
(2)若 BE=1,ED=2 求 BD 的长.
03 复习自测
一、选择题(每小题4分,共40分)
1.如图,在 ABCD中,连接AC.已知∠BAC=40°,∠ACB=80°,则∠BCD= ( )
A.80° B.100° C.120° D.140°
2.已知直角三角形的两直角边长分别是 12 和5,则斜边上的中线长是 ( )
A.34 B.26 C.8.5 D.6.5
3.若正方形的一条对角线长为4,则这个正方形的面积是 ( )
A.8 D.16
4.如图,在 Rt△ABC中,∠A=30°,BC=1,D,E分别是直角边BC,AC 的中点,则 DE的长为 ( )
A.1 B.2
C.
5.矩形、菱形、正方形都具有的性质是 ( )
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.每一条对角线平分一组对角
6.已知在四边形ABCD中,对角线 AC 与 BD相交于点O,AD∥BC,则下列判断错误的是
( )
A.如果 AB=CD,AC=BD,那么四边形ABCD 是矩形
B.如果 AB∥CD,OA=OB,那么四边形ABCD是矩形
C.如果 AD=BC,AC⊥BD,那么四边形ABCD 是菱形
D.如果 OA=OC,AC⊥BD,那么四边形ABCD 是菱形
7.如图,在菱形ABCD中,BD=8,AC=6,过点D作 DE⊥BA,交 BA 的延长线于点 E,则DE的长为 ( )
A. B. C. D.
8.如图,在矩形ABCD中,E,F 分别是AD,BC的中点,连接AF,BE,CE,DF,分别相交于点M,N,则四边形EMFN是 ( )
A.正方形 B.菱形
C.矩形 D.无法确定
9.如图,O为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形.若AB=2,则OE 的长为 ( )
A. B. D.2
10.如图,在菱形 ABCD中,∠B=60°,点 P 从点 B 出发,沿折线 BC—CD 移动,移动到点D停止.在△ABP 形状的变化过程中,依次出现的特殊三角形是 ( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
二、填空题(每小题4分,共20分)
11.若平行四边形中的两个内角度数比为1:2,则其中较大内角的度数是 度.
12.如图,矩形 ABCD的对角线AC 与BD 相交于点O,∠ADB=30°,AB=6,则OC的长为
13.(2023·宜昌)如图,小宇将一张平行四边形纸片折叠,使点 A 落在长边CD 上的点A'处,并得到折痕DE.小宇测得长边 CD=8,则四边形 A'EBC 的周长为 .
14.如图,这是利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,∠1=60°,则在墙上悬挂晾衣架的两个铁钉 A,B之间的距离为 cm.
15.(2023·湘潭)七巧板是我国民间广为流传的一种益智玩具.某同学用边长为4d m的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形、1个正方形和1个平行四边形组成,则图中阴影部分的面积为 dm .
三、解答题(共40分)
16.(8分)如图,在四边形 ABCD 中,BE⊥AC,DF⊥AC,垂足分别为 E,F,且 BE=DF,AF=CE.求证:四边形ABCD为平行四边形.
17.(10分)(2023·鞍山)如图,在□ABCD中,对角线 BD的垂直平分线分别与AD,BD,BC相交于点E,O,F,连接BE,DF.求证:四边形 EBFD是菱形.
18.(10分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD 的中点,EF⊥AB于点F,OG∥EF,交AB于点G.
(1)求证:四边形OEFG是矩形.
(2)若AC=8,BD=6,则矩形OEFG的周长为 .
19.(12分)如图,在正方形 ABCD 中,E为AD上一点,连接 BE,BE 的垂直平分线交AB于点 M,交 CD 于点 N,垂足为O,点 F 在DC 上,且MF∥AD.
(1)求证:△ABE≌△FMN.
(2)若AB=8,AE=6,求ON的长.
期末复习(三) 平行四边形
【例1】 证明:∵四边形ABCD是平行四边形,∴AB∥CD.∴∠ABE=∠FCE.∵OE是△ABC的中位线,∴E是BC 的中点.∴BE=CE.
在△ABE 和△FCE 中, ∴△ABE≌△FCE
(ASA).∴AB=CF.又∵AB∥CF,∴四边形ABFC是平行四边形.
【例2】 解:(1)证明:∵△ABC和△DEF 是两个边长为10cm的等边三角形,∴AC=DF,∠ACD=∠FDE=60°.∴AC∥DF.∴四边形ADFC是平行四边形.(2)①图1略,当t=3时,□ADFC是菱形.理由如下:∵t=3,∴点B与点D 重合,点C与点E 重合.又∵△ABC和△DEF是两个边长为10cm的等边三角形,∴AD=DF=FE=EA.∴□ADFC是菱形.②可能.图2略,∵□ADFC是矩形,∴∠DAC=90°.又∵∠ACD=60°,∴∠ADC=30°,∴DC=2AC=20cm,AD=10 cm.∴点 B与点E重合,t=(3+10)÷1=13(s),S矩形ADFc=AD
变式训练
1.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,AD=BC.∴∠E=∠DCE.∵AE+CD=AD,∴AE+AB=BE=BC.∴∠E=∠BCE.∴∠DCE=∠BCE,即CE平分∠BCD.
2.解:(1)证明:∵四边形 ABCD是矩形,∴AD∥BC,∠ADC=∠C=90°.∵EF∥DC,∴四边形 EFDC 为平行四边形.∵DE 平分∠ADC,∴∠ADE=∠CDE.∵AD∥BC,∴∠ADE=∠DEC.∴∠CDE=∠DEC.∴CD=CE.∴平行四边形 EFDC是菱形.又∵∠C=90°,∴菱形EFDC是正方形.(2)∵四边形 EFDC是正方形,ED=2 ,∴CE=CD=2.∴BC=BE+EC=1+2=3.∴在Rt△BCD中,
复习自测
1. C 2. D 3. A 4. A 5. C 6. A 7. B 8. B 9. B 10. C11.120 12.6 13.16 14.60 15.2
16.证明:∵BE⊥AC,DF⊥AC,∴∠BEC=∠DFA=90°.在△BCE和△DAF中,CEBEAN,∠DFA,∴△BCE≌△DAF(SA). CEB=AD,∠BCE=∠DAF.∴BC∥AD.∴四边形ABCD是平行四边形.
17.证明:∵四边形 ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠EDO=∠FBO.∵EF为BD 的垂直平分线,∴BO=DO,EF⊥BD.在△DEO 和△BFO 中, ∴△DEO≌△BFO(ASA).∴OE=OF.∴四边形EBFD是平行四边形.又∵EF⊥BD,∴平行四边形EBFD是菱形.
18.解:(1)证明:∵四边形ABCD 是菱形,∴OB=OD.∵E是AD的中点,∴OE是△ABD的中位线.∴OE∥AB.∵OG∥EF,∴四边形OEFG是平行四边形.∵EF⊥AB,∴∠EFG=90°.∴平行四边形OEFG 是矩形.(2)9.8
19.解:(1)证明:∵四边形ABCD为正方形,∴AB=AD,AB∥CD.又∵MF∥AD,∴四边形AMFD为矩形.∴AD=MF.∴AB=FM.∴∠MFN=∠BAE=90°.又∵MN为BE 的垂直平分线,∴∠FMN+∠BMO=∠BMO+∠ABE=90°.∴∠FMN=∠ABE.
在△ABE和△FMN中, ∴△ABE≌△FMN
(ASA).(2)连接ME.∵MN为BE 的垂直平分线,∴BM=EM.设BM=ME=x,∴AM=8-x.在 Rt△AME中, AE ,即 解得 10MO,解得MO= .∵△ABE≌△FMN,∴MN=BE=10.∴
01 知识结构图
02 重难点突破
重难点1 平行四边形的性质与判定
【例1】 如图,在 ABCD中,O是对角线AC 与 BD 的交点,OE 是△ABC 的中位线,连接 AE 并延长,与DC 的延长线相交于点 F,连接BF.求证:四边形 ABFC是平行四边形.
【思路点拨】 由□ABCD 可得AB∥CD,则∠ABE=∠FCE,由OE 是△ABC 的中位线,易得 E 是边 BC 的中点,从而证得△ABE≌△FCE,得AB=CF.进而证得四边形 ABFC是平行四边形.
【解答】
变式训练
1.如图,四边形 ABCD 是平行四边形,延长 BA至点E,使AE+CD=AD,连接CE.求证:CE平分∠BCD.
重难点2 特殊平行四边形的性质与判定
【例2】 如图,已知△ABC 和△DEF是两个边长为10cm的等边三角形,且点 B,D,C,E在同一条直线上,连接AD,CF.
(1)求证:四边形 ADFC是平行四边形.
(2)若 BD=3c m,△ABC 沿射线 BE 的方向以1 cm/s的速度运动.设△ABC 的运动时间为 t s.
①当t为何值时,□ADFC 是菱形 请说明理由.
②□ADFC有可能是矩形吗 若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
【思路点拨】 (1)由△ABC 和△DEF是两个边长为 10 cm 的等边三角形,得AC=DF,∠ACD=∠FDE=60°,从而得 AC∥DF,所以四边形ADFC是平行四边形;(2)①若□ADFC是菱形,则点 B 与点 D 重合,从而得出△ABC沿射线BE 的方向移动的距离,进而求出运动的时间;②若 ADFC是矩形,则∠DAC=90°,从而可推断点 E 与点B 重合,得出△ABC 沿射线BE 的方向移动的距离,进而求出运动的时间及此矩形的面积.
【解答】
变式训练
2.如图,在矩形 ABCD中,E是边BC 上一点,DE平分∠ADC,EF∥DC,交边 AD于点F,连接 BD.
(1)求证:四边形 EFDC是正方形.
(2)若 BE=1,ED=2 求 BD 的长.
03 复习自测
一、选择题(每小题4分,共40分)
1.如图,在 ABCD中,连接AC.已知∠BAC=40°,∠ACB=80°,则∠BCD= ( )
A.80° B.100° C.120° D.140°
2.已知直角三角形的两直角边长分别是 12 和5,则斜边上的中线长是 ( )
A.34 B.26 C.8.5 D.6.5
3.若正方形的一条对角线长为4,则这个正方形的面积是 ( )
A.8 D.16
4.如图,在 Rt△ABC中,∠A=30°,BC=1,D,E分别是直角边BC,AC 的中点,则 DE的长为 ( )
A.1 B.2
C.
5.矩形、菱形、正方形都具有的性质是 ( )
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.每一条对角线平分一组对角
6.已知在四边形ABCD中,对角线 AC 与 BD相交于点O,AD∥BC,则下列判断错误的是
( )
A.如果 AB=CD,AC=BD,那么四边形ABCD 是矩形
B.如果 AB∥CD,OA=OB,那么四边形ABCD是矩形
C.如果 AD=BC,AC⊥BD,那么四边形ABCD 是菱形
D.如果 OA=OC,AC⊥BD,那么四边形ABCD 是菱形
7.如图,在菱形ABCD中,BD=8,AC=6,过点D作 DE⊥BA,交 BA 的延长线于点 E,则DE的长为 ( )
A. B. C. D.
8.如图,在矩形ABCD中,E,F 分别是AD,BC的中点,连接AF,BE,CE,DF,分别相交于点M,N,则四边形EMFN是 ( )
A.正方形 B.菱形
C.矩形 D.无法确定
9.如图,O为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形.若AB=2,则OE 的长为 ( )
A. B. D.2
10.如图,在菱形 ABCD中,∠B=60°,点 P 从点 B 出发,沿折线 BC—CD 移动,移动到点D停止.在△ABP 形状的变化过程中,依次出现的特殊三角形是 ( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
二、填空题(每小题4分,共20分)
11.若平行四边形中的两个内角度数比为1:2,则其中较大内角的度数是 度.
12.如图,矩形 ABCD的对角线AC 与BD 相交于点O,∠ADB=30°,AB=6,则OC的长为
13.(2023·宜昌)如图,小宇将一张平行四边形纸片折叠,使点 A 落在长边CD 上的点A'处,并得到折痕DE.小宇测得长边 CD=8,则四边形 A'EBC 的周长为 .
14.如图,这是利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,∠1=60°,则在墙上悬挂晾衣架的两个铁钉 A,B之间的距离为 cm.
15.(2023·湘潭)七巧板是我国民间广为流传的一种益智玩具.某同学用边长为4d m的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形、1个正方形和1个平行四边形组成,则图中阴影部分的面积为 dm .
三、解答题(共40分)
16.(8分)如图,在四边形 ABCD 中,BE⊥AC,DF⊥AC,垂足分别为 E,F,且 BE=DF,AF=CE.求证:四边形ABCD为平行四边形.
17.(10分)(2023·鞍山)如图,在□ABCD中,对角线 BD的垂直平分线分别与AD,BD,BC相交于点E,O,F,连接BE,DF.求证:四边形 EBFD是菱形.
18.(10分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD 的中点,EF⊥AB于点F,OG∥EF,交AB于点G.
(1)求证:四边形OEFG是矩形.
(2)若AC=8,BD=6,则矩形OEFG的周长为 .
19.(12分)如图,在正方形 ABCD 中,E为AD上一点,连接 BE,BE 的垂直平分线交AB于点 M,交 CD 于点 N,垂足为O,点 F 在DC 上,且MF∥AD.
(1)求证:△ABE≌△FMN.
(2)若AB=8,AE=6,求ON的长.
期末复习(三) 平行四边形
【例1】 证明:∵四边形ABCD是平行四边形,∴AB∥CD.∴∠ABE=∠FCE.∵OE是△ABC的中位线,∴E是BC 的中点.∴BE=CE.
在△ABE 和△FCE 中, ∴△ABE≌△FCE
(ASA).∴AB=CF.又∵AB∥CF,∴四边形ABFC是平行四边形.
【例2】 解:(1)证明:∵△ABC和△DEF 是两个边长为10cm的等边三角形,∴AC=DF,∠ACD=∠FDE=60°.∴AC∥DF.∴四边形ADFC是平行四边形.(2)①图1略,当t=3时,□ADFC是菱形.理由如下:∵t=3,∴点B与点D 重合,点C与点E 重合.又∵△ABC和△DEF是两个边长为10cm的等边三角形,∴AD=DF=FE=EA.∴□ADFC是菱形.②可能.图2略,∵□ADFC是矩形,∴∠DAC=90°.又∵∠ACD=60°,∴∠ADC=30°,∴DC=2AC=20cm,AD=10 cm.∴点 B与点E重合,t=(3+10)÷1=13(s),S矩形ADFc=AD
变式训练
1.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,AD=BC.∴∠E=∠DCE.∵AE+CD=AD,∴AE+AB=BE=BC.∴∠E=∠BCE.∴∠DCE=∠BCE,即CE平分∠BCD.
2.解:(1)证明:∵四边形 ABCD是矩形,∴AD∥BC,∠ADC=∠C=90°.∵EF∥DC,∴四边形 EFDC 为平行四边形.∵DE 平分∠ADC,∴∠ADE=∠CDE.∵AD∥BC,∴∠ADE=∠DEC.∴∠CDE=∠DEC.∴CD=CE.∴平行四边形 EFDC是菱形.又∵∠C=90°,∴菱形EFDC是正方形.(2)∵四边形 EFDC是正方形,ED=2 ,∴CE=CD=2.∴BC=BE+EC=1+2=3.∴在Rt△BCD中,
复习自测
1. C 2. D 3. A 4. A 5. C 6. A 7. B 8. B 9. B 10. C11.120 12.6 13.16 14.60 15.2
16.证明:∵BE⊥AC,DF⊥AC,∴∠BEC=∠DFA=90°.在△BCE和△DAF中,CEBEAN,∠DFA,∴△BCE≌△DAF(SA). CEB=AD,∠BCE=∠DAF.∴BC∥AD.∴四边形ABCD是平行四边形.
17.证明:∵四边形 ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠EDO=∠FBO.∵EF为BD 的垂直平分线,∴BO=DO,EF⊥BD.在△DEO 和△BFO 中, ∴△DEO≌△BFO(ASA).∴OE=OF.∴四边形EBFD是平行四边形.又∵EF⊥BD,∴平行四边形EBFD是菱形.
18.解:(1)证明:∵四边形ABCD 是菱形,∴OB=OD.∵E是AD的中点,∴OE是△ABD的中位线.∴OE∥AB.∵OG∥EF,∴四边形OEFG是平行四边形.∵EF⊥AB,∴∠EFG=90°.∴平行四边形OEFG 是矩形.(2)9.8
19.解:(1)证明:∵四边形ABCD为正方形,∴AB=AD,AB∥CD.又∵MF∥AD,∴四边形AMFD为矩形.∴AD=MF.∴AB=FM.∴∠MFN=∠BAE=90°.又∵MN为BE 的垂直平分线,∴∠FMN+∠BMO=∠BMO+∠ABE=90°.∴∠FMN=∠ABE.
在△ABE和△FMN中, ∴△ABE≌△FMN
(ASA).(2)连接ME.∵MN为BE 的垂直平分线,∴BM=EM.设BM=ME=x,∴AM=8-x.在 Rt△AME中, AE ,即 解得 10MO,解得MO= .∵△ABE≌△FMN,∴MN=BE=10.∴
同课章节目录
