勾股定理期末复习(二) 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 勾股定理期末复习(二) 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 08:55:19 | ||
图片预览



文档简介
勾股定理期末复习(二)
01 知识结构图
02 重难点突破
重难点1 勾股定理的证明
【例1】 勾股定理神秘而美妙,它的证法多种多样,其巧妙各有不同.其中“面积法”给了小聪以灵感.他惊喜地发现,当两个全等的直角三角形按图1或图 2 的方式摆放时,都可以用“面积法”来证明勾股定理,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示的方式摆放,其中∠DAB=90°.求证:(
证明:连接 DB,过点 D 作 BC 边上的高DF,垂足为F,则 DF=EC=b--a.
又
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示的方式摆放,其中∠DAB=90°.求证:(
【解答】
方 法 指导
勾股定理的证明是用面积法证明恒等式,通过不同的方式表 示同一个图形的面积.
变式训练
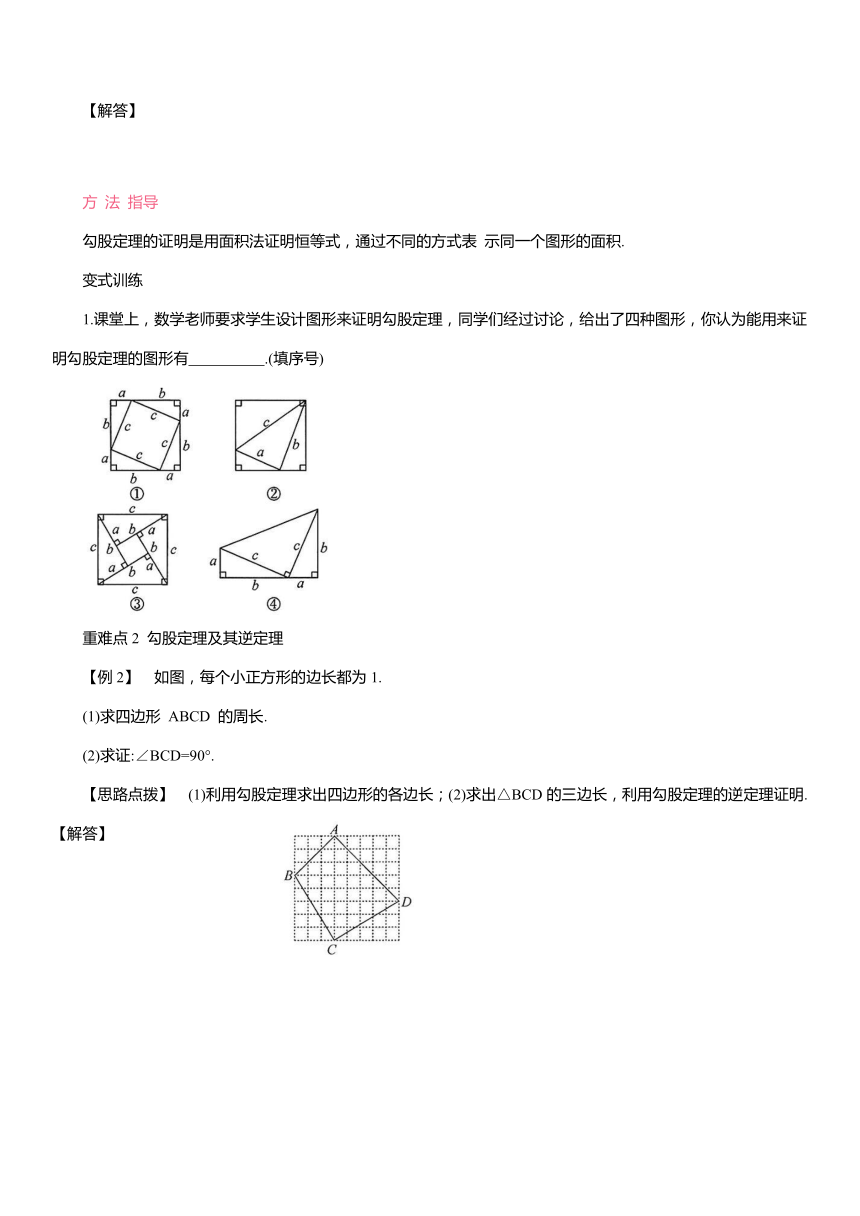
1.课堂上,数学老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出了四种图形,你认为能用来证明勾股定理的图形有 .(填序号)
重难点2 勾股定理及其逆定理
【例2】 如图,每个小正方形的边长都为1.
(1)求四边形 ABCD 的周长.
(2)求证:∠BCD=90°.
【思路点拨】 (1)利用勾股定理求出四边形的各边长;(2)求出△BCD的三边长,利用勾股定理的逆定理证明.【解答】
方 法 指导
正方形网格中的两个格点之间的距离可以用勾股定理求出.勾股定理的逆定理是证明一个角等于90°的一种思路.本题的第(2)问还可以通过两个三角形全等来证明.
变式训练
2.如图,在正方形纸片 ABCD 上有一点 P,PA=1,PD=2,PC=3.现将△PCD剪下,并将它拼到如图所示的位置(C与A 重合,P与G 重合,D与D 重合).求:
(1)线段 PG的长.
(2)∠APD的度数.
重难点3 勾股定理在实际生活中的应用
【例3】 如图,高速公路的一侧有A,B两个村庄,它们到高速公路所在直线 MN 的距离分别为 现要在高速公路上 A B 之间设一个出口 P,使A,B两个村庄到 P 的距离之和最短,则这个最短距离是多少千米
【思路点拨】 运用“两点之间,线段最短”先确定出点 P在A B 上的位置,再利用勾股定理求出AP+BP的长.
【解答】
方 法 指导
解这类题的关键在于运用几何知识正确找到符合条件的点的位置,会构造直角三角形,利用勾股定理把三角形中有一个直角的“形”的特征,转化为三边“数”的关系,因此它是数形结合的一个典范.
变式训练
3.在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点 C 与公路上的停靠站A 的距离为300 米,与公路上另一停靠站 B 的距离为 400 米,且 CA⊥CB,如图.为了安全起见,爆破点 C 周围半径250 米范围内不得进入,问在进行爆破时,公路AB段是否有危险 是否需要暂时封锁 请通过计算进行说明.
思想方法 方程思想
【例4】 如图,在Rt△ABC 中, ∠B = 90°,AB=3,BC=4,将△ABC 折叠,使点 B 恰好落在边 AC上,与点 B'重合,AE 为折痕,则EB'的长为 .
方法 指导
方程思想常在勾股定理与折叠问题中出现,利用折叠的性质得到边、角相等,进而把条件转化到一个直角三角形中,利用勾股定理构建方程,从而求出线段长度.
变式训练
4.如图,在长方形 ABCD 中,BC=6,CD=3,将△BCD沿对角线 BD 翻折,点C 落在点C'处,BC'交AD 于点E,则线段 DE 的长为 .
03 复习自测
一、选择题(每小题5分,共40分)
1.在 Rt△ABC中,∠C=90°,AB=8,AC=5,则BC 的长是 ( )
A.3 C.7 D.
2.小新将一根铁丝剪成九段,分成三组:①2 cm,3 cm,4 cm;②3 cm,4 cm,5 cm;③9 cm,40 cm,41 cm.分别以每组铁丝围成三角形,能构成直角三角形的有 ( )
A.② B.①②
C.①③ D.②③
3.下列各命题的逆命题成立的是 ( )
A.全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等
D.如果两个角都是45°,那么这两个角相等
4.如图所示的是办公桌摆件示意图,四边形ABCD 是矩形,若对角线 AC⊥EO,垂足是E,AB=15 cm,BC= 8cm,AE=25 cm,则CE= ( )
A.6 cm B.7 cm C. 8cm D.9 cm
5. 新考向 数学文化如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成.若∠AEB=90°,AB=13 cm,BE=5cm ,则阴影部分的面积是 ( )
B.25 cm
C.49 cm D.64 cm
6.如图,数轴上点 A,B分别对应数1,2.过点 B作PQ⊥AB,以点 B 为圆心、AB 的长为半径画弧,交 PQ于点C,以原点O为圆心、OC 的长为半径画弧,交数轴于点 M,则点 M 对应的数是 ( )
A. B. C. D.
7.如图,图1是由边长为1的六个小正方形组成的图形,它可以围成图2所示的正方体,则图1中正方形的顶点 A,B在图2围成的正方体中的距离是 ( )
A.0 B.1 C. D.
8.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.当AC=4,BC=2时,阴影部分的面积为 ( )
A.4
B.4π
C.8π
D.8
二、填空题(每小题5分,共20分)
9.如果三角形的三边长分别为 ,,2,那么这个三角形的最大角的度数为 .
10.小红同学先朝正东方向行进了4k m,再朝正北方向行进了8km,此时小红离出发点的距离是 km.
11.如图,在 Rt△ABC中,∠ACB=90°,∠A=30°,BC=2cm .把△ABC 沿AB 方向平移1cm,得到△A'B'C',连接 CC',则四边形AB'C'C的周长为 cm.
12.将三角板置于两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度(每块砖的厚度相等)为 cm.
三、解答题(共40分)
13.(10 分)如图,已知某山的高度 AC 为 800米,在山上 A 处与山下 B 处各建一个索道口,且 BC=1500米,欢欢从山下索道口坐缆车到山顶.已知缆车每分钟走50米,那么大约多少分钟后,欢欢才能达到山顶
14.(14分)如图,在等边三角形ABC中,点 D,E分别在边 BC,AC上.若 CD=2,过点 D 作DE∥AB,过点 E作EF⊥DE,交 BC的延长线于点 F,求 EF 的长.
15.(16分)给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称.
(2)如图,将△ABC绕顶点 B 按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.求证:
①△BCE 是等边三角形.
即四边形ABCD 是勾股四边形.
期末复习(二) 勾股定理
【例1】 证明:连接BD,过点 B作DE 边上的高BF,垂足为 F,则 BF 又
【例2】 解:(1)根据勾股定理,得. AD=5 ,∴四边形 ABCD的周长为8 +2 .(2)证明:连接BD.∵BC= ,CD= ,DB= ,∴BC +CD =BD .∴△BCD是直角三角形,即∠BCD=90°.
【例3】 解:作点 B关于直线MN 的对称点 B',连接AB'交A B 于点P,则AP+BP=AP+PB'=AB',易知点 P 即为到A,B距离之和最短的点.过点 A 作AE⊥BB'于点 E,则 .由勾股定理,得 即AP+BP=AB'=10km.答:出口P到A,B两村庄的距离之和最短是10 km.
【例4】 1.5
变式训练
1.①③④
2.解:(1)根据题意,得△AGD≌△CPD,∴∠GDA=∠PDC.又∵∠ADC=90°,∴∠GDP=90°.又∵GD=PD=2,∴PG=2 .(2)∵AG=CP=3,AP=1,PG=2 ,∴AP +PG =AG .∴△APG为直角三角形,∠APG=90°.由(1)得,△PGD为等腰直角三角形,∠GPD=45°,∴∠APD=∠APG+∠GPD=135°.
3.解:过点C作CD⊥AB于点D.∵BC=400米,AC=300米,∠ACB=90°,∴根据勾股定理,得AB=500米. AC,∴CD=240米.∵240<250,∴有危险,∴AB段公路需要暂时封锁.
4.
复习自测
1. B 2. D 3. C 4. C 5. C 6. B 7. C 8. A 9.90° 10.4 11.(8+2
13.解:根据题意,得∠ACB=90°.在 Rt△ABC中,根据勾股定理,得 0(米).1700÷50=34(分).答:大约34分钟后,欢欢才能达到山顶.
14.解:∵△ABC是等边三角形,∴∠B=∠ACB=60°.∵DE∥AB,∴∠EDC=∠B=60°.∴△EDC 是等边三角形.∴DE=DC=2.在Rt△DEF中,∵∠DEF=90°,∠EDF=60°,DE=2,∴∠F=30°,
15.解:(1)正方形、矩形.(2)证明:①∵△ABC≌△DBE,∴BC=BE.∵∠CBE=60°,∴△BCE 是等边三角形.②∵△ABC≌△DBE,
∴AC=ED.∵△BCE为等边三角形,∴BC=CE,∠BCE=60°.∵∠DCB=30°,∴∠DCE=90°.在 Rt△DCE中, ,即四边形ABCD 是勾股四边形.
01 知识结构图
02 重难点突破
重难点1 勾股定理的证明
【例1】 勾股定理神秘而美妙,它的证法多种多样,其巧妙各有不同.其中“面积法”给了小聪以灵感.他惊喜地发现,当两个全等的直角三角形按图1或图 2 的方式摆放时,都可以用“面积法”来证明勾股定理,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示的方式摆放,其中∠DAB=90°.求证:(
证明:连接 DB,过点 D 作 BC 边上的高DF,垂足为F,则 DF=EC=b--a.
又
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示的方式摆放,其中∠DAB=90°.求证:(
【解答】
方 法 指导
勾股定理的证明是用面积法证明恒等式,通过不同的方式表 示同一个图形的面积.
变式训练
1.课堂上,数学老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出了四种图形,你认为能用来证明勾股定理的图形有 .(填序号)
重难点2 勾股定理及其逆定理
【例2】 如图,每个小正方形的边长都为1.
(1)求四边形 ABCD 的周长.
(2)求证:∠BCD=90°.
【思路点拨】 (1)利用勾股定理求出四边形的各边长;(2)求出△BCD的三边长,利用勾股定理的逆定理证明.【解答】
方 法 指导
正方形网格中的两个格点之间的距离可以用勾股定理求出.勾股定理的逆定理是证明一个角等于90°的一种思路.本题的第(2)问还可以通过两个三角形全等来证明.
变式训练
2.如图,在正方形纸片 ABCD 上有一点 P,PA=1,PD=2,PC=3.现将△PCD剪下,并将它拼到如图所示的位置(C与A 重合,P与G 重合,D与D 重合).求:
(1)线段 PG的长.
(2)∠APD的度数.
重难点3 勾股定理在实际生活中的应用
【例3】 如图,高速公路的一侧有A,B两个村庄,它们到高速公路所在直线 MN 的距离分别为 现要在高速公路上 A B 之间设一个出口 P,使A,B两个村庄到 P 的距离之和最短,则这个最短距离是多少千米
【思路点拨】 运用“两点之间,线段最短”先确定出点 P在A B 上的位置,再利用勾股定理求出AP+BP的长.
【解答】
方 法 指导
解这类题的关键在于运用几何知识正确找到符合条件的点的位置,会构造直角三角形,利用勾股定理把三角形中有一个直角的“形”的特征,转化为三边“数”的关系,因此它是数形结合的一个典范.
变式训练
3.在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点 C 与公路上的停靠站A 的距离为300 米,与公路上另一停靠站 B 的距离为 400 米,且 CA⊥CB,如图.为了安全起见,爆破点 C 周围半径250 米范围内不得进入,问在进行爆破时,公路AB段是否有危险 是否需要暂时封锁 请通过计算进行说明.
思想方法 方程思想
【例4】 如图,在Rt△ABC 中, ∠B = 90°,AB=3,BC=4,将△ABC 折叠,使点 B 恰好落在边 AC上,与点 B'重合,AE 为折痕,则EB'的长为 .
方法 指导
方程思想常在勾股定理与折叠问题中出现,利用折叠的性质得到边、角相等,进而把条件转化到一个直角三角形中,利用勾股定理构建方程,从而求出线段长度.
变式训练
4.如图,在长方形 ABCD 中,BC=6,CD=3,将△BCD沿对角线 BD 翻折,点C 落在点C'处,BC'交AD 于点E,则线段 DE 的长为 .
03 复习自测
一、选择题(每小题5分,共40分)
1.在 Rt△ABC中,∠C=90°,AB=8,AC=5,则BC 的长是 ( )
A.3 C.7 D.
2.小新将一根铁丝剪成九段,分成三组:①2 cm,3 cm,4 cm;②3 cm,4 cm,5 cm;③9 cm,40 cm,41 cm.分别以每组铁丝围成三角形,能构成直角三角形的有 ( )
A.② B.①②
C.①③ D.②③
3.下列各命题的逆命题成立的是 ( )
A.全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等
D.如果两个角都是45°,那么这两个角相等
4.如图所示的是办公桌摆件示意图,四边形ABCD 是矩形,若对角线 AC⊥EO,垂足是E,AB=15 cm,BC= 8cm,AE=25 cm,则CE= ( )
A.6 cm B.7 cm C. 8cm D.9 cm
5. 新考向 数学文化如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成.若∠AEB=90°,AB=13 cm,BE=5cm ,则阴影部分的面积是 ( )
B.25 cm
C.49 cm D.64 cm
6.如图,数轴上点 A,B分别对应数1,2.过点 B作PQ⊥AB,以点 B 为圆心、AB 的长为半径画弧,交 PQ于点C,以原点O为圆心、OC 的长为半径画弧,交数轴于点 M,则点 M 对应的数是 ( )
A. B. C. D.
7.如图,图1是由边长为1的六个小正方形组成的图形,它可以围成图2所示的正方体,则图1中正方形的顶点 A,B在图2围成的正方体中的距离是 ( )
A.0 B.1 C. D.
8.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.当AC=4,BC=2时,阴影部分的面积为 ( )
A.4
B.4π
C.8π
D.8
二、填空题(每小题5分,共20分)
9.如果三角形的三边长分别为 ,,2,那么这个三角形的最大角的度数为 .
10.小红同学先朝正东方向行进了4k m,再朝正北方向行进了8km,此时小红离出发点的距离是 km.
11.如图,在 Rt△ABC中,∠ACB=90°,∠A=30°,BC=2cm .把△ABC 沿AB 方向平移1cm,得到△A'B'C',连接 CC',则四边形AB'C'C的周长为 cm.
12.将三角板置于两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度(每块砖的厚度相等)为 cm.
三、解答题(共40分)
13.(10 分)如图,已知某山的高度 AC 为 800米,在山上 A 处与山下 B 处各建一个索道口,且 BC=1500米,欢欢从山下索道口坐缆车到山顶.已知缆车每分钟走50米,那么大约多少分钟后,欢欢才能达到山顶
14.(14分)如图,在等边三角形ABC中,点 D,E分别在边 BC,AC上.若 CD=2,过点 D 作DE∥AB,过点 E作EF⊥DE,交 BC的延长线于点 F,求 EF 的长.
15.(16分)给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称.
(2)如图,将△ABC绕顶点 B 按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.求证:
①△BCE 是等边三角形.
即四边形ABCD 是勾股四边形.
期末复习(二) 勾股定理
【例1】 证明:连接BD,过点 B作DE 边上的高BF,垂足为 F,则 BF 又
【例2】 解:(1)根据勾股定理,得. AD=5 ,∴四边形 ABCD的周长为8 +2 .(2)证明:连接BD.∵BC= ,CD= ,DB= ,∴BC +CD =BD .∴△BCD是直角三角形,即∠BCD=90°.
【例3】 解:作点 B关于直线MN 的对称点 B',连接AB'交A B 于点P,则AP+BP=AP+PB'=AB',易知点 P 即为到A,B距离之和最短的点.过点 A 作AE⊥BB'于点 E,则 .由勾股定理,得 即AP+BP=AB'=10km.答:出口P到A,B两村庄的距离之和最短是10 km.
【例4】 1.5
变式训练
1.①③④
2.解:(1)根据题意,得△AGD≌△CPD,∴∠GDA=∠PDC.又∵∠ADC=90°,∴∠GDP=90°.又∵GD=PD=2,∴PG=2 .(2)∵AG=CP=3,AP=1,PG=2 ,∴AP +PG =AG .∴△APG为直角三角形,∠APG=90°.由(1)得,△PGD为等腰直角三角形,∠GPD=45°,∴∠APD=∠APG+∠GPD=135°.
3.解:过点C作CD⊥AB于点D.∵BC=400米,AC=300米,∠ACB=90°,∴根据勾股定理,得AB=500米. AC,∴CD=240米.∵240<250,∴有危险,∴AB段公路需要暂时封锁.
4.
复习自测
1. B 2. D 3. C 4. C 5. C 6. B 7. C 8. A 9.90° 10.4 11.(8+2
13.解:根据题意,得∠ACB=90°.在 Rt△ABC中,根据勾股定理,得 0(米).1700÷50=34(分).答:大约34分钟后,欢欢才能达到山顶.
14.解:∵△ABC是等边三角形,∴∠B=∠ACB=60°.∵DE∥AB,∴∠EDC=∠B=60°.∴△EDC 是等边三角形.∴DE=DC=2.在Rt△DEF中,∵∠DEF=90°,∠EDF=60°,DE=2,∴∠F=30°,
15.解:(1)正方形、矩形.(2)证明:①∵△ABC≌△DBE,∴BC=BE.∵∠CBE=60°,∴△BCE 是等边三角形.②∵△ABC≌△DBE,
∴AC=ED.∵△BCE为等边三角形,∴BC=CE,∠BCE=60°.∵∠DCB=30°,∴∠DCE=90°.在 Rt△DCE中, ,即四边形ABCD 是勾股四边形.
同课章节目录
