北师大版2024-2025学年八年级(下)期末数学模拟试卷3(含解析)
文档属性
| 名称 | 北师大版2024-2025学年八年级(下)期末数学模拟试卷3(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:10:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2024-2025学年八年级(下)期末数学模拟试卷3
学校:___________姓名:___________班级:___________考号:___________
一.选择题(本大题共12小题,每小题3分,共36分)
1.如图图形中,是中心对称图形的是( )
A. B.
C. D.
2.若一个正多边形的每个内角均为108°,则这个多边形是( )
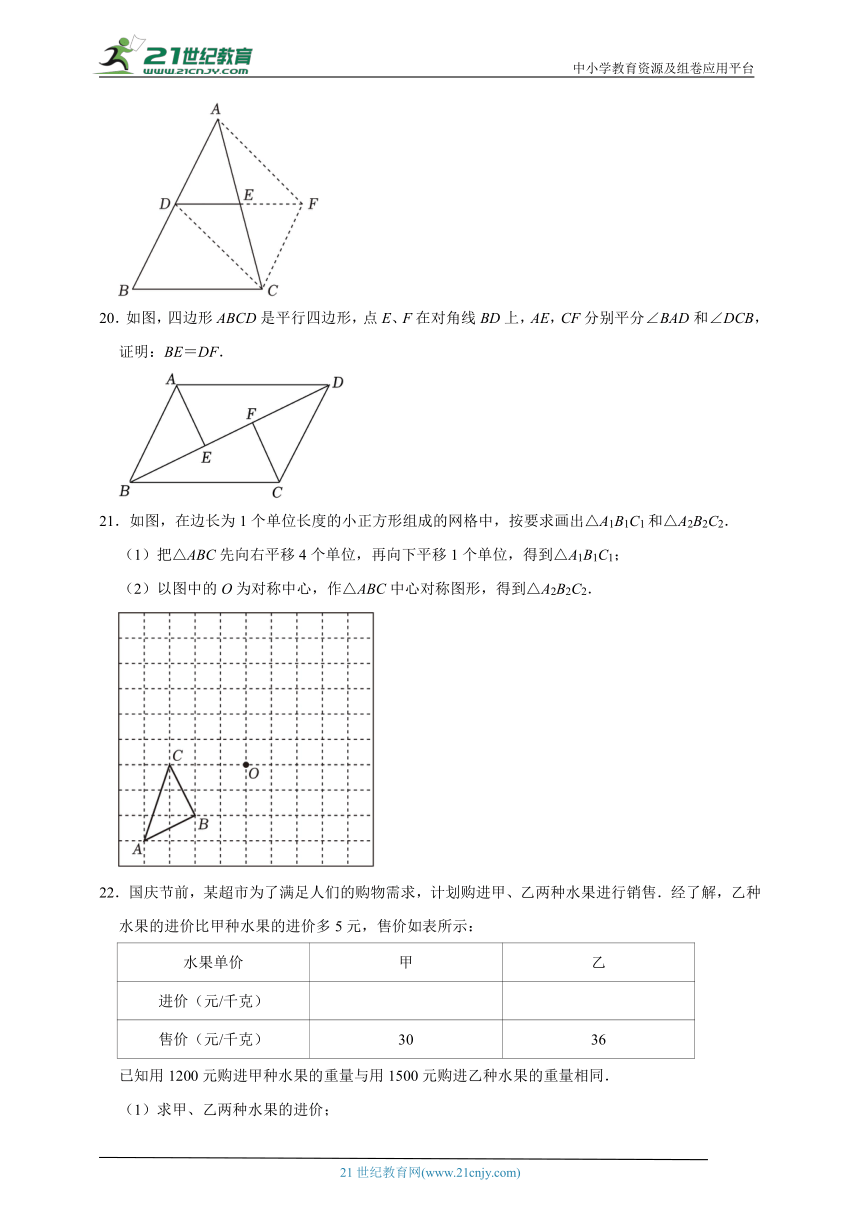
A.正四边形 B.正五边形 C.正六边形 D.正八边形
3.不等式x>1的解集在数轴上表示正确的是( )
A. B.
C. D.
4.小明准备用自己的零花钱买一台价值1000元的英语学习机,现在已存100元,如果从现在起每月节省30元,设x个月后,他存够了所需钱数,则x应满足的关系式是( )
A.30x﹣100≥1000 B.30x+100≥1000
C.30x﹣100≤1000 D.30x+100≤1000
5.若 ABCD的周长为32,AB=4,则BC的长是( )
A.6 B.8 C.12 D.16
6.如图,∠AOB是一钢架,∠AOB=18°,为使钢架更加牢固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE的长度相等,则最多能添加的钢管根数为( )
A.4 B.5 C.6 D.无数
7.在用反证法证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.若用反证法证明“若a>b,b>c,则a>c”,则应假设( )
A.a<b,b<c B.a≤b,b≤c C.a<c D.a≤c
8.若分式2016,则分式的值等于( )
A. B. C. D.
9.如图,在△ABC中,AB=5,AC=4,BC=8,AI平分∠BAC,CI平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
A.8 B.9 C.10 D.10.5
10.甲、乙两人分别从距目的地6km和10km的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20min到达目的地,设甲的速度为x km/min,则可列方程为( )
A. B.
C. D.
11.如果x﹣y=﹣2,xy=5,则计算x2y﹣xy2的结果为( )
A.﹣7 B.3 C.﹣10 D.10
12.如图,在 ABCD中,对角线AC与BD相交于点O,E,F是对角线AC上的点.下列条件不能判定四边形BEDF为平行四边形的是( )
A.DE∥BF B.AE=CF C.∠BEO=∠DFO D.BE=DF
二.填空题(本大题共4小题,每小题4分,共16分)
13.不等式x≤5的正整数解有 个.
14.关于x的二次三项式x2+mx﹣6因式分解的结果是(x+3)(x﹣2),则m= .
15.如图,在周长为24cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为 .
16.如图,等边△ABC内部一点O,OA=4,OB=3,OC=5,将线段BO以点B为旋转中心逆时针旋转60°,得到线段BO′,连接O′A,则∠AOB= .
三.解答题(本大题共9小题,共98分)
17.(1)解方程:;
(2)不等式组:.
18.先化简,再求值:,其中,.
19.在八下书本49页中,我们得到了三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.完成以下证明过程:
已知:如图,D、E分别是△ABC的边AB,AC的中点;
求证:DE∥BC且.
证明:如图,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE= ,DE=EF,
∴四边形ADCF是平行四边形,( )(填推理的依据)
CF平行且等于DA,∴CF平行且等于BD.
∴四边形DBCF是平行四边形,( )(填推理的依据)
∴DF平行且等于BC.又∵,∴DE∥BC,.
20.如图,四边形ABCD是平行四边形,点E、F在对角线BD上,AE,CF分别平分∠BAD和∠DCB,证明:BE=DF.
21.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2.
(1)把△ABC先向右平移4个单位,再向下平移1个单位,得到△A1B1C1;
(2)以图中的O为对称中心,作△ABC中心对称图形,得到△A2B2C2.
22.国庆节前,某超市为了满足人们的购物需求,计划购进甲、乙两种水果进行销售.经了解,乙种水果的进价比甲种水果的进价多5元,售价如表所示:
水果单价 甲 乙
进价(元/千克)
售价(元/千克) 30 36
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)求甲、乙两种水果的进价;
(2)若超市购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则超市应如何进货才能获得最大利润,最大利润是多少?
23.浙教版教材八年级下册第5章“4.2平行四边形及其性质(3)”中有这样一道例题:
如图,在平行四边形ABCD中,对角线AC,BD交于点E,AC⊥BC,若AC=4,AB=5,求BD的长.请你完成求解过程.
小明的解题过程如下:在平行四边形ABCD中∵AC=4,AB=5,∴第①步∵AC⊥BC∴第②步∴第③步∴第④步
你认为他的解题过程正确吗?若正确,请再用其他方法求出BD的长;若不正确,请指出错误(从第几步开始错),并求出正确的BD长.
24.把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.如:①用配方法分解因式:a2+4a+3,解:原式=a2+4a+4﹣1=(a+2)2﹣1
=(a+2+1)(a+2﹣l)=(a+3)(a+l)
②M=a2﹣2a+6,利用配方法求M的最小值:
解:M=a2﹣2a+6=a2﹣2a+1+5=(a﹣1)2+5
因为(a﹣1)2≥0,所以当a=1时,M有最小值5
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式x2﹣8x+ ;
(2)用配方法因式分解x2﹣4xy﹣12y2;
(3)若M=4x2+2x﹣1,求M的最小值.
25.如图,E为△ABC边BC的中点,DE⊥BC,交△ABC的外角∠BAM的平分线于点D,DF⊥AB于F,且AB>AC.
(1)求证:CD=BD;
(2)求证:BF=AC+AF.
参考答案
一.选择题(共12小题)
1.【考点】中心对称图形
【分析】利用中心对称图形的定义即可得出答案.
解:观察四个选项可知,只有B选项中的图形绕某一点旋转180°后能与自身重合,
因此B选项中的图形是中心对称图形,
故选:B.
【点评】本题考查中心对称图形的识别,掌握定义是解题的关键.平面内,如果把一个图形绕着某一点旋转180°后能与自身重合,那么这个图形叫做中心对称图形.
2.【考点】多边形内角与外角
【分析】根据正多边形外角和为360°与正多边形性质即可得到答案.
解:∵一个正多边形的每个内角均为108°,
∴180°﹣108°=72°,
∴,
∴这个多边形是正五边形,
故选:B.
【点评】本题考查多边形的内角与外角,熟练掌握正多边形外角与内角关系是解决问题的关键.
3.【考点】在数轴上表示不等式的解集
【分析】根据在数轴上表示的不等式的解集的方法得出答案即可.
解:不等式x>1的解集在数轴上表示为:
故选:A.
【点评】本题考查在数轴上表示不等式的解集,掌握不等式的解集在数轴上的表示方法是正确判断的前提.
4.【考点】由实际问题抽象出一元一次不等式
【分析】此题中的不等关系:现在已存有100元,计划从现在起以后每个月节省30元,直到他至少有1000元.j据此列出方程结可求解.
解:x个月可以节省30x元,
根据题意,得30x+100≥1000.
故选:B.
【点评】本题主要考查由实际问题抽象出一元一次不等式,抓住关键词语,弄清不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.
5.【考点】平行四边形的性质
【分析】根据平行四边形的性质得到AB=CD,AD=BC,根据2(AB+BC)=32,即可求出答案.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是32,
∴2(AB+BC)=32,
∴BC=12.
故选:C.
【点评】本题主要考查对平行四边形的性质的理解和掌握,能利用平行四边形的性质进行计算是解此题的关键.
6.【考点】等腰三角形的性质
【分析】根据已知利用等腰三角形的性质及三角形外角的性质,找出图中存在的规律,根据规律及三角形的内角和定理不难求解.
解:∵添加的钢管长度都与OE相等,∠AOB=18°,
∴∠GEF=∠FGE=36°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是18°,第二个是36°,第三个是54°,四个是72°,五个是90°就不存在了.
所以一共有4个.
故选:A.
【点评】此题考查了三角形的内角和是180度的性质和等腰三角形的性质及三角形外角的性质;发现并利用规律是正确解答本题的关键.
7.【考点】反证法;不等式的性质
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,a>c的反面是a≤c.
解:用反证法证明“若a>b,b>c,则a>c”,
应假设a≤c,
故选:D.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
8.【考点】分式的加减法;分式的值
【分析】利用等式的性质将已知条件变形得到x﹣y=﹣2016xy,再利用整体的思想方法利用整体代入的方法化简运算即可.
解:∵2016,
∴x﹣y=﹣2016xy,
∴原式
.
故选:B.
【点评】本题主要考查了分式的化简运算,利用等式的性质将已知条件变形得到x﹣y=﹣2016xy,再利用整体的思想方法解答是解题的关键.
9.【考点】平移的性质
【分析】根据角平分线的定义以及平行线的性质,可得出∠ABI=∠MBI=∠MIB,∠ACI=∠NCI=∠NIC,由等腰三角形的判定可得MI=MB,NI=NC,由三角形周长的定义即可得出答案.
解:如图,连接BI,
∵AI平分∠BAC,CI平分∠ACB,
∴BI平分∠ABC,
由平移的性质可知,MI∥AB,NI∥AC,
∴∠ABI=∠MBI=∠MIB,∠ACI=∠NCI=∠NIC,
∴MI=MB,NI=NC,
∴阴影部分的周长为MI+MN+NI=MB+MN+NC=BC=8,
故选:A.
【点评】本题考查平移的性质,角平分线以及平行线的性质,理解平移的性质,掌握角平分线的定义以及平行线的性质是正确解答的前提.
10.【考点】由实际问题抽象出分式方程
【分析】求的是速度,路程明显,一定是根据时间来列等量关系,本题的关键描述语是:甲比乙提前20分钟到达目的地.等量关系为:乙走10千米用的时间﹣甲走6千米用的时间=20分钟.
解:设甲的速度为x km/min,则,则乙的速度为x km/min,则.
根据题意,得20.
整理,得
故选:D.
【点评】本题考查由实际问题抽象出分式方程,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
11.【考点】因式分解的应用
【分析】分解因式并整体代入即可求解.
解:先分解因式得:
x2y﹣xy2=xy(x﹣y),
当x﹣y=﹣2,xy=5时,原式=5×(﹣2)=﹣10,
故选:C.
【点评】本题考查了因式分解的应用,熟练掌握因式分解是关键.
12.【考点】平行四边形的判定与性质;全等三角形的判定与性质
【分析】根据平行线 到现在得到∠EDO=∠FBO,根据全等三角形的性质得到DE=BF,求得四边形BEDF是平行四边形,故A不符合题意;根据平行四边形的性质得到AB∥CD,AB=CD,AD∥BC,AD=BC,OA=OC,OB=OD,推出四边形BEDF是平行四边形,故B不符合题意;根据全等三角形的性质得到BE=DF,∠AEB=∠CFD,求得DF∥BE,得到四边形BEDF是平行四边形,故C不符合题意;根据平行线的判定定理得到BE∥DF,根据平行四边形的判定定理得到四边形BEDF是平行四边形,故C不符合题意;当BE=DF,此时不能得到△ADE≌△CBF,△DOE≌△BOF,即不能证明DE=BF,添加BE=DF不能判定四边形BEDF是平行四边形,故D符合题意.
解:∵DE∥BF,
∴∠EDO=∠FBO,
∵∠DOE=∠BOF,OD=OB,
∴△DOE≌△BOF(ASA),
∴DE=BF,
∴四边形BEDF是平行四边形,故A不符合题意;
∵平行四边形ABCD,
∴AB∥CD,AB=CD,AD∥BC,AD=BC,OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,故B不符合题意;
∵AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵∠ABE=∠CDF,
∴△ABE≌△CDF(ASA),
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴DF∥BE,
∴四边形BEDF是平行四边形,故C不符合题意;
∵∠BEO=∠DFO,
∴BE∥DF,
∵DE∥BF,
∴四边形BEDF是平行四边形,故C不符合题意;
当BE=DF,此时不能得到:△ADE≌△CBF,△DOE≌△BOF,即不能证明DE=BF,添加BE=DF不能判定四边形BEDF是平行四边形,故D符合题意;
故选:D.
【点评】本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定和性质定理是解题的关键.
二.填空题(共4小题)
13.【考点】一元一次不等式的整数解
【分析】本题考查不等式的整数解,求出不等式x≤5的正整数解即可解答.
解:不等式x≤5的正整数解为x=1,2,3,4,5,共5个.
故答案为:5.
【点评】本题主要考查一元一次不等式的整数解,解题的关键是掌握解一元一次不等式的步骤及解和解集的概念.
14.【考点】因式分解﹣十字相乘法等
【分析】先根据多项式乘多项式法则计算(x+3)(x﹣2),然后根据已知条件求出m即可.
解:(x+3)(x﹣2)
=x2﹣2x+3x﹣6
=x2+x﹣6,
∵关于x的二次三项式x2+mx﹣6因式分解的结果是(x+3)(x﹣2),
∴m=1,
故答案为:1.
【点评】本题主要考查了分解因式,解题关键是熟练掌握多项式乘多项式法则.
15.【考点】平行四边形的性质;线段垂直平分线的性质
【分析】根据平行四边形的性质求出AB+AD=12cm,根据线段的垂直平分线求出DE=BE,求出△ABE的周长等于AB+AD,代入求出即可.
解:∵平行四边形ABCD,
∴AD=BC,AB=CD,OB=OD,
∵OE⊥BD,
∴BE=DE,
∵平行四边形ABCD的周长是24cm,
∴2AB+2AD=24cm,
∴AB+AD=12cm,
∴△ABE的周长是AB+AE+BE=AB+AE+DE=AB+AD=12cm,
故答案为:12cm.
【点评】本题考查了线段垂直平分线性质和平行四边形的性质的应用,关键是求出AD+AB的长和求出△ABE的周长=AB+AD,题目具有一定的代表性,难度也不大,是一道比较好的题目.
16.【考点】旋转的性质;全等三角形的判定与性质;等边三角形的性质;勾股定理
【分析】连接OO',由将线段BO以点B为旋转中心逆时针旋转60°,得到线段BO′,可得∠OBO'=60°,OB=O'B,故△BOO'是等边三角形,可得∠BOO'=60°,OO'=OB=3,而△ABC是等边三角形,即得∠ABC=60°=∠OBO',AB=BC,可证△ABO'≌△CBO(SAS),即知AO'=OC=5,有OO'2+OA2=AO'2,∠AOO'=90°,从而∠AOB=∠AOO'+∠BOO'=150°.
解:连接OO',如图:
∵将线段BO以点B为旋转中心逆时针旋转60°,得到线段BO′,
∴∠OBO'=60°,OB=O'B,
∴△BOO'是等边三角形,
∴∠BOO'=60°,OO'=OB=3,
∵△ABC是等边三角形,
∴∠ABC=60°=∠OBO',AB=BC,
∴∠ABO'=∠CBO,
∴△ABO'≌△CBO(SAS),
∴AO'=OC=5,
∵OO'2+OA2=32+42=25,AO'2=25,
∴OO'2+OA2=AO'2,
∴∠AOO'=90°,
∴∠AOB=∠AOO'+∠BOO'=90°+60°=150°,
故答案为:150°.
【点评】本题考查旋转的性质,涉及等边三角形性质,全等三角形判定与性质,勾股定理逆定理等知识,解题的关键是掌握全等三角形的判定定理.
三.解答题(共9小题)
17.【考点】解分式方程;解一元一次不等式组
【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解:(1)去分母得:2(1﹣x)﹣3(1+x)=﹣6,
去括号得:2﹣2x﹣3﹣3x=﹣6,
移项合并得:﹣5x=﹣5,
解得:x=1,
检验:把x=1代入得:(1+x)(1﹣x)=0,
∴x=1是增根,分式方程无解;
(2),
由①得:x≥﹣1,
由②得:x<2,
∴不等式组的解集为﹣1≤x<2.
【点评】此题考查了解分式方程,以及解一元一次不等式组,熟练掌握各自的解法是解本题的关键.
18.【考点】分式的化简求值
【分析】先根据分式混合运算法则进行化简,然后将数据代入求值即可.
解:原式
=a+b,
把,代入得:
原式.
【点评】本题主要考查了分式化简求值,熟练掌握分式混合运算法则,是解题的关键.
19.【考点】平行四边形的判定与性质;三角形中位线定理
【分析】先证四边形ADCF是平行四边形,则CF平行且等于DA,得CF平行且等于BD.再证四边形DBCF是平行四边形,得DF平行且等于BC,即可得出结论.
证明:如图,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,(对角线互相平分的四边形是平行四边形)(填推理的依据)
CF平行且等于DA,
∴CF平行且等于BD.
∴四边形DBCF是平行四边形,(一组对边平行且相等的四边形是平行四边形)(填推理的依据)
∴DF平行且等于BC.
又∵.
∴DE∥BC,.
故答案为:EC;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
【点评】本题考查了平行四边形的判定与性质、三角形中位线定理等知识;熟练掌握三角形中位线定理,证明四边形DBCF为平行四边形是解题的关键.
20.【考点】平行四边形的性质;全等三角形的判定与性质
【分析】先由平行四边形的性质得到AB∥CD,AB=CD,∠BAD=∠DCB,求得∠ABE=∠CDF,再证△ABE≌△CDF(ASA),然后由全等三角形的性质即可得到结论.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD.
∴∠ABE=∠CDF.
∵AE,CF分别平分∠BAD和∠DCB,
∴,.
∵∠BAD=∠BCD,
∴∠BAE=∠DCF.
在△BAE与△DCF中,
,
∴△BAE≌△DCF(ASA).
∴BE=DF.
【点评】本题考查了平行四边形的性质、全等三角形的判定和性质以及平行线的性质等知识,熟练掌握平行四边形的性质,证明三角形全等是解题的关键,属于中考常考题型.
21.【考点】作图﹣旋转变换;作图﹣平移变换
【分析】(1)把A、B、C三点先向右平移4个单位,再向下平移1个单位得到A1,B1,C1,顺次连接得到的各点即可;
(2)利用中心对称的性质分别作出A,B,C的对应点A2,B2,C2,顺次连接得到的各点即可.
解:(1)如图1,△A1B1C1即为所求:
;
(2)如图2,△A2B2C2即为所求:
.
【点评】本题主要考查了作图﹣旋转变换以及作图﹣平移变换,解题的关键是掌握旋转变换的性质,属于中考常考题型.
22.【考点】分式方程的应用;一元一次不等式组的应用
【分析】(1)设甲种水果的进价为x元,则乙种水果的进价为(x+5)元,由题意:用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.列出分式方程,解方程即可;
(2)设购进甲种水果m千克,则乙种水果(150﹣m)千克,利润为y元,由题意得y=﹣m+1650,再由甲种水果的重量不低于乙种水果重量的2倍,得m≥2(150﹣m),解得m≥100,然后由一次函数的性质即可得出结论.
解:(1)设甲种水果的进价为x元,则乙种水果的进价为(x+5)元,
由题意得:,
解得:x=20,
经检验:x=20是原方程的解,且符合题意,
则x+5=25,
答:甲种水果的进价为20元,则乙种水果的进价为25元;
(2)设购进甲种水果m千克,则乙种水果(150﹣m)千克,利润为y元,
由题意得:y=(30﹣20)m+(36﹣25)(150﹣m)=﹣m+1650,
∵甲种水果的重量不低于乙种水果重量的2倍,
∴m≥2(150﹣m),
解得:m≥100,
∵﹣1<0,则y随m的增大而减小,
∴当m=100时,y最大,最大值=﹣100+1650=1550,
则150﹣m=50,
答:购进甲种水果100千克,乙种水果50千克才能获得最大利润,最大利润为1550元.
【点评】本题考查了分式方程的应用、一元一次不等式的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找出数量关系,正确列出一元一次不等式.
23.【考点】平行四边形的判定与性质;勾股定理
【分析】利用平行四边形的性质求得EA=EC=2,EB=ED,利用勾股定理先后求得BC和BE,据此求解即可.
解:小明的解题过程不正确,从第③步开始错;
在平行四边形ABCD中,
∵AC=4,AB=5,
∴EA=ECAC4=2,EB=ED,
∵AC⊥BC,
∴,
∴BE,
∴BD=2EB=2.
【点评】本题考查了平行四边形的性质,勾股定理,关键是根据平行四边形的对角线相互平分解答.
24.【考点】因式分解﹣十字相乘法等;非负数的性质:偶次方;因式分解﹣分组分解法
【分析】(1)利用完全平方公式,加上一次项系数一半的平方即可;
(2)利用十字相乘法分解因式;
(3)利用配方法得到M=4(x)2,然后根据非负数的性质确定M的最小值.
解:(1)x2﹣8x+42=(x﹣4)2,
故答案为:16;
(2)x2﹣4xy﹣12y2=(x﹣6y)(x+2y);
(3)M=4x2+2x﹣1=4(x2x)﹣1
=4[x2x+()2﹣()2]﹣1
=4(x)2,
∵4(x)2≥0,
∴当x时,M有最小值.
【点评】本题考查了因式分解﹣十字相乘法等,熟练掌握因式分解的方法和配方法是解决问题的关键.
25.【考点】全等三角形的判定与性质;角平分线的性质;线段垂直平分线的性质
【分析】(1)利用线段的垂直平分线的性质证明即可;
(2)证明△AFD≌△AND(AAS),推出AF=AN,DF=DN,再证明△BFD≌△CND(HL),可得结论.
(1)证明:∵E为△ABC边BC的中点,DE⊥BC,
∴CD=BD;
(2)证明:过点D作DN⊥MC于点N,
∵AD为∠BAM角平分线,
∴∠DAN=∠DAF,
∵DN⊥MC,DF⊥AB,
∴∠AFD=∠AND,
在△AFD和△AND中,
,
∴△AFD≌△AND(AAS),
∴AF=AN,DF=DN,
∵∠BFD=∠CND=90°,
在Rt△BFD和Rt△CND中,
,
∴△BFD≌△CND(HL),
∴BF=CN=AC+AN=AC+AF.
【点评】本题考查了全等三角形的判定与性质,角平分线的性质,线段的垂直平分线的性质等知识,解题的关键是正确寻找全等三角形解决问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版2024-2025学年八年级(下)期末数学模拟试卷3
学校:___________姓名:___________班级:___________考号:___________
一.选择题(本大题共12小题,每小题3分,共36分)
1.如图图形中,是中心对称图形的是( )
A. B.
C. D.
2.若一个正多边形的每个内角均为108°,则这个多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正八边形
3.不等式x>1的解集在数轴上表示正确的是( )
A. B.
C. D.
4.小明准备用自己的零花钱买一台价值1000元的英语学习机,现在已存100元,如果从现在起每月节省30元,设x个月后,他存够了所需钱数,则x应满足的关系式是( )
A.30x﹣100≥1000 B.30x+100≥1000
C.30x﹣100≤1000 D.30x+100≤1000
5.若 ABCD的周长为32,AB=4,则BC的长是( )
A.6 B.8 C.12 D.16
6.如图,∠AOB是一钢架,∠AOB=18°,为使钢架更加牢固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE的长度相等,则最多能添加的钢管根数为( )
A.4 B.5 C.6 D.无数
7.在用反证法证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.若用反证法证明“若a>b,b>c,则a>c”,则应假设( )
A.a<b,b<c B.a≤b,b≤c C.a<c D.a≤c
8.若分式2016,则分式的值等于( )
A. B. C. D.
9.如图,在△ABC中,AB=5,AC=4,BC=8,AI平分∠BAC,CI平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
A.8 B.9 C.10 D.10.5
10.甲、乙两人分别从距目的地6km和10km的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20min到达目的地,设甲的速度为x km/min,则可列方程为( )
A. B.
C. D.
11.如果x﹣y=﹣2,xy=5,则计算x2y﹣xy2的结果为( )
A.﹣7 B.3 C.﹣10 D.10
12.如图,在 ABCD中,对角线AC与BD相交于点O,E,F是对角线AC上的点.下列条件不能判定四边形BEDF为平行四边形的是( )
A.DE∥BF B.AE=CF C.∠BEO=∠DFO D.BE=DF
二.填空题(本大题共4小题,每小题4分,共16分)
13.不等式x≤5的正整数解有 个.
14.关于x的二次三项式x2+mx﹣6因式分解的结果是(x+3)(x﹣2),则m= .
15.如图,在周长为24cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为 .
16.如图,等边△ABC内部一点O,OA=4,OB=3,OC=5,将线段BO以点B为旋转中心逆时针旋转60°,得到线段BO′,连接O′A,则∠AOB= .
三.解答题(本大题共9小题,共98分)
17.(1)解方程:;
(2)不等式组:.
18.先化简,再求值:,其中,.
19.在八下书本49页中,我们得到了三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.完成以下证明过程:
已知:如图,D、E分别是△ABC的边AB,AC的中点;
求证:DE∥BC且.
证明:如图,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE= ,DE=EF,
∴四边形ADCF是平行四边形,( )(填推理的依据)
CF平行且等于DA,∴CF平行且等于BD.
∴四边形DBCF是平行四边形,( )(填推理的依据)
∴DF平行且等于BC.又∵,∴DE∥BC,.
20.如图,四边形ABCD是平行四边形,点E、F在对角线BD上,AE,CF分别平分∠BAD和∠DCB,证明:BE=DF.
21.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2.
(1)把△ABC先向右平移4个单位,再向下平移1个单位,得到△A1B1C1;
(2)以图中的O为对称中心,作△ABC中心对称图形,得到△A2B2C2.
22.国庆节前,某超市为了满足人们的购物需求,计划购进甲、乙两种水果进行销售.经了解,乙种水果的进价比甲种水果的进价多5元,售价如表所示:
水果单价 甲 乙
进价(元/千克)
售价(元/千克) 30 36
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)求甲、乙两种水果的进价;
(2)若超市购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则超市应如何进货才能获得最大利润,最大利润是多少?
23.浙教版教材八年级下册第5章“4.2平行四边形及其性质(3)”中有这样一道例题:
如图,在平行四边形ABCD中,对角线AC,BD交于点E,AC⊥BC,若AC=4,AB=5,求BD的长.请你完成求解过程.
小明的解题过程如下:在平行四边形ABCD中∵AC=4,AB=5,∴第①步∵AC⊥BC∴第②步∴第③步∴第④步
你认为他的解题过程正确吗?若正确,请再用其他方法求出BD的长;若不正确,请指出错误(从第几步开始错),并求出正确的BD长.
24.把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.如:①用配方法分解因式:a2+4a+3,解:原式=a2+4a+4﹣1=(a+2)2﹣1
=(a+2+1)(a+2﹣l)=(a+3)(a+l)
②M=a2﹣2a+6,利用配方法求M的最小值:
解:M=a2﹣2a+6=a2﹣2a+1+5=(a﹣1)2+5
因为(a﹣1)2≥0,所以当a=1时,M有最小值5
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式x2﹣8x+ ;
(2)用配方法因式分解x2﹣4xy﹣12y2;
(3)若M=4x2+2x﹣1,求M的最小值.
25.如图,E为△ABC边BC的中点,DE⊥BC,交△ABC的外角∠BAM的平分线于点D,DF⊥AB于F,且AB>AC.
(1)求证:CD=BD;
(2)求证:BF=AC+AF.
参考答案
一.选择题(共12小题)
1.【考点】中心对称图形
【分析】利用中心对称图形的定义即可得出答案.
解:观察四个选项可知,只有B选项中的图形绕某一点旋转180°后能与自身重合,
因此B选项中的图形是中心对称图形,
故选:B.
【点评】本题考查中心对称图形的识别,掌握定义是解题的关键.平面内,如果把一个图形绕着某一点旋转180°后能与自身重合,那么这个图形叫做中心对称图形.
2.【考点】多边形内角与外角
【分析】根据正多边形外角和为360°与正多边形性质即可得到答案.
解:∵一个正多边形的每个内角均为108°,
∴180°﹣108°=72°,
∴,
∴这个多边形是正五边形,
故选:B.
【点评】本题考查多边形的内角与外角,熟练掌握正多边形外角与内角关系是解决问题的关键.
3.【考点】在数轴上表示不等式的解集
【分析】根据在数轴上表示的不等式的解集的方法得出答案即可.
解:不等式x>1的解集在数轴上表示为:
故选:A.
【点评】本题考查在数轴上表示不等式的解集,掌握不等式的解集在数轴上的表示方法是正确判断的前提.
4.【考点】由实际问题抽象出一元一次不等式
【分析】此题中的不等关系:现在已存有100元,计划从现在起以后每个月节省30元,直到他至少有1000元.j据此列出方程结可求解.
解:x个月可以节省30x元,
根据题意,得30x+100≥1000.
故选:B.
【点评】本题主要考查由实际问题抽象出一元一次不等式,抓住关键词语,弄清不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.
5.【考点】平行四边形的性质
【分析】根据平行四边形的性质得到AB=CD,AD=BC,根据2(AB+BC)=32,即可求出答案.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是32,
∴2(AB+BC)=32,
∴BC=12.
故选:C.
【点评】本题主要考查对平行四边形的性质的理解和掌握,能利用平行四边形的性质进行计算是解此题的关键.
6.【考点】等腰三角形的性质
【分析】根据已知利用等腰三角形的性质及三角形外角的性质,找出图中存在的规律,根据规律及三角形的内角和定理不难求解.
解:∵添加的钢管长度都与OE相等,∠AOB=18°,
∴∠GEF=∠FGE=36°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是18°,第二个是36°,第三个是54°,四个是72°,五个是90°就不存在了.
所以一共有4个.
故选:A.
【点评】此题考查了三角形的内角和是180度的性质和等腰三角形的性质及三角形外角的性质;发现并利用规律是正确解答本题的关键.
7.【考点】反证法;不等式的性质
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,a>c的反面是a≤c.
解:用反证法证明“若a>b,b>c,则a>c”,
应假设a≤c,
故选:D.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
8.【考点】分式的加减法;分式的值
【分析】利用等式的性质将已知条件变形得到x﹣y=﹣2016xy,再利用整体的思想方法利用整体代入的方法化简运算即可.
解:∵2016,
∴x﹣y=﹣2016xy,
∴原式
.
故选:B.
【点评】本题主要考查了分式的化简运算,利用等式的性质将已知条件变形得到x﹣y=﹣2016xy,再利用整体的思想方法解答是解题的关键.
9.【考点】平移的性质
【分析】根据角平分线的定义以及平行线的性质,可得出∠ABI=∠MBI=∠MIB,∠ACI=∠NCI=∠NIC,由等腰三角形的判定可得MI=MB,NI=NC,由三角形周长的定义即可得出答案.
解:如图,连接BI,
∵AI平分∠BAC,CI平分∠ACB,
∴BI平分∠ABC,
由平移的性质可知,MI∥AB,NI∥AC,
∴∠ABI=∠MBI=∠MIB,∠ACI=∠NCI=∠NIC,
∴MI=MB,NI=NC,
∴阴影部分的周长为MI+MN+NI=MB+MN+NC=BC=8,
故选:A.
【点评】本题考查平移的性质,角平分线以及平行线的性质,理解平移的性质,掌握角平分线的定义以及平行线的性质是正确解答的前提.
10.【考点】由实际问题抽象出分式方程
【分析】求的是速度,路程明显,一定是根据时间来列等量关系,本题的关键描述语是:甲比乙提前20分钟到达目的地.等量关系为:乙走10千米用的时间﹣甲走6千米用的时间=20分钟.
解:设甲的速度为x km/min,则,则乙的速度为x km/min,则.
根据题意,得20.
整理,得
故选:D.
【点评】本题考查由实际问题抽象出分式方程,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
11.【考点】因式分解的应用
【分析】分解因式并整体代入即可求解.
解:先分解因式得:
x2y﹣xy2=xy(x﹣y),
当x﹣y=﹣2,xy=5时,原式=5×(﹣2)=﹣10,
故选:C.
【点评】本题考查了因式分解的应用,熟练掌握因式分解是关键.
12.【考点】平行四边形的判定与性质;全等三角形的判定与性质
【分析】根据平行线 到现在得到∠EDO=∠FBO,根据全等三角形的性质得到DE=BF,求得四边形BEDF是平行四边形,故A不符合题意;根据平行四边形的性质得到AB∥CD,AB=CD,AD∥BC,AD=BC,OA=OC,OB=OD,推出四边形BEDF是平行四边形,故B不符合题意;根据全等三角形的性质得到BE=DF,∠AEB=∠CFD,求得DF∥BE,得到四边形BEDF是平行四边形,故C不符合题意;根据平行线的判定定理得到BE∥DF,根据平行四边形的判定定理得到四边形BEDF是平行四边形,故C不符合题意;当BE=DF,此时不能得到△ADE≌△CBF,△DOE≌△BOF,即不能证明DE=BF,添加BE=DF不能判定四边形BEDF是平行四边形,故D符合题意.
解:∵DE∥BF,
∴∠EDO=∠FBO,
∵∠DOE=∠BOF,OD=OB,
∴△DOE≌△BOF(ASA),
∴DE=BF,
∴四边形BEDF是平行四边形,故A不符合题意;
∵平行四边形ABCD,
∴AB∥CD,AB=CD,AD∥BC,AD=BC,OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,故B不符合题意;
∵AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵∠ABE=∠CDF,
∴△ABE≌△CDF(ASA),
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴DF∥BE,
∴四边形BEDF是平行四边形,故C不符合题意;
∵∠BEO=∠DFO,
∴BE∥DF,
∵DE∥BF,
∴四边形BEDF是平行四边形,故C不符合题意;
当BE=DF,此时不能得到:△ADE≌△CBF,△DOE≌△BOF,即不能证明DE=BF,添加BE=DF不能判定四边形BEDF是平行四边形,故D符合题意;
故选:D.
【点评】本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定和性质定理是解题的关键.
二.填空题(共4小题)
13.【考点】一元一次不等式的整数解
【分析】本题考查不等式的整数解,求出不等式x≤5的正整数解即可解答.
解:不等式x≤5的正整数解为x=1,2,3,4,5,共5个.
故答案为:5.
【点评】本题主要考查一元一次不等式的整数解,解题的关键是掌握解一元一次不等式的步骤及解和解集的概念.
14.【考点】因式分解﹣十字相乘法等
【分析】先根据多项式乘多项式法则计算(x+3)(x﹣2),然后根据已知条件求出m即可.
解:(x+3)(x﹣2)
=x2﹣2x+3x﹣6
=x2+x﹣6,
∵关于x的二次三项式x2+mx﹣6因式分解的结果是(x+3)(x﹣2),
∴m=1,
故答案为:1.
【点评】本题主要考查了分解因式,解题关键是熟练掌握多项式乘多项式法则.
15.【考点】平行四边形的性质;线段垂直平分线的性质
【分析】根据平行四边形的性质求出AB+AD=12cm,根据线段的垂直平分线求出DE=BE,求出△ABE的周长等于AB+AD,代入求出即可.
解:∵平行四边形ABCD,
∴AD=BC,AB=CD,OB=OD,
∵OE⊥BD,
∴BE=DE,
∵平行四边形ABCD的周长是24cm,
∴2AB+2AD=24cm,
∴AB+AD=12cm,
∴△ABE的周长是AB+AE+BE=AB+AE+DE=AB+AD=12cm,
故答案为:12cm.
【点评】本题考查了线段垂直平分线性质和平行四边形的性质的应用,关键是求出AD+AB的长和求出△ABE的周长=AB+AD,题目具有一定的代表性,难度也不大,是一道比较好的题目.
16.【考点】旋转的性质;全等三角形的判定与性质;等边三角形的性质;勾股定理
【分析】连接OO',由将线段BO以点B为旋转中心逆时针旋转60°,得到线段BO′,可得∠OBO'=60°,OB=O'B,故△BOO'是等边三角形,可得∠BOO'=60°,OO'=OB=3,而△ABC是等边三角形,即得∠ABC=60°=∠OBO',AB=BC,可证△ABO'≌△CBO(SAS),即知AO'=OC=5,有OO'2+OA2=AO'2,∠AOO'=90°,从而∠AOB=∠AOO'+∠BOO'=150°.
解:连接OO',如图:
∵将线段BO以点B为旋转中心逆时针旋转60°,得到线段BO′,
∴∠OBO'=60°,OB=O'B,
∴△BOO'是等边三角形,
∴∠BOO'=60°,OO'=OB=3,
∵△ABC是等边三角形,
∴∠ABC=60°=∠OBO',AB=BC,
∴∠ABO'=∠CBO,
∴△ABO'≌△CBO(SAS),
∴AO'=OC=5,
∵OO'2+OA2=32+42=25,AO'2=25,
∴OO'2+OA2=AO'2,
∴∠AOO'=90°,
∴∠AOB=∠AOO'+∠BOO'=90°+60°=150°,
故答案为:150°.
【点评】本题考查旋转的性质,涉及等边三角形性质,全等三角形判定与性质,勾股定理逆定理等知识,解题的关键是掌握全等三角形的判定定理.
三.解答题(共9小题)
17.【考点】解分式方程;解一元一次不等式组
【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解:(1)去分母得:2(1﹣x)﹣3(1+x)=﹣6,
去括号得:2﹣2x﹣3﹣3x=﹣6,
移项合并得:﹣5x=﹣5,
解得:x=1,
检验:把x=1代入得:(1+x)(1﹣x)=0,
∴x=1是增根,分式方程无解;
(2),
由①得:x≥﹣1,
由②得:x<2,
∴不等式组的解集为﹣1≤x<2.
【点评】此题考查了解分式方程,以及解一元一次不等式组,熟练掌握各自的解法是解本题的关键.
18.【考点】分式的化简求值
【分析】先根据分式混合运算法则进行化简,然后将数据代入求值即可.
解:原式
=a+b,
把,代入得:
原式.
【点评】本题主要考查了分式化简求值,熟练掌握分式混合运算法则,是解题的关键.
19.【考点】平行四边形的判定与性质;三角形中位线定理
【分析】先证四边形ADCF是平行四边形,则CF平行且等于DA,得CF平行且等于BD.再证四边形DBCF是平行四边形,得DF平行且等于BC,即可得出结论.
证明:如图,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,(对角线互相平分的四边形是平行四边形)(填推理的依据)
CF平行且等于DA,
∴CF平行且等于BD.
∴四边形DBCF是平行四边形,(一组对边平行且相等的四边形是平行四边形)(填推理的依据)
∴DF平行且等于BC.
又∵.
∴DE∥BC,.
故答案为:EC;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
【点评】本题考查了平行四边形的判定与性质、三角形中位线定理等知识;熟练掌握三角形中位线定理,证明四边形DBCF为平行四边形是解题的关键.
20.【考点】平行四边形的性质;全等三角形的判定与性质
【分析】先由平行四边形的性质得到AB∥CD,AB=CD,∠BAD=∠DCB,求得∠ABE=∠CDF,再证△ABE≌△CDF(ASA),然后由全等三角形的性质即可得到结论.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD.
∴∠ABE=∠CDF.
∵AE,CF分别平分∠BAD和∠DCB,
∴,.
∵∠BAD=∠BCD,
∴∠BAE=∠DCF.
在△BAE与△DCF中,
,
∴△BAE≌△DCF(ASA).
∴BE=DF.
【点评】本题考查了平行四边形的性质、全等三角形的判定和性质以及平行线的性质等知识,熟练掌握平行四边形的性质,证明三角形全等是解题的关键,属于中考常考题型.
21.【考点】作图﹣旋转变换;作图﹣平移变换
【分析】(1)把A、B、C三点先向右平移4个单位,再向下平移1个单位得到A1,B1,C1,顺次连接得到的各点即可;
(2)利用中心对称的性质分别作出A,B,C的对应点A2,B2,C2,顺次连接得到的各点即可.
解:(1)如图1,△A1B1C1即为所求:
;
(2)如图2,△A2B2C2即为所求:
.
【点评】本题主要考查了作图﹣旋转变换以及作图﹣平移变换,解题的关键是掌握旋转变换的性质,属于中考常考题型.
22.【考点】分式方程的应用;一元一次不等式组的应用
【分析】(1)设甲种水果的进价为x元,则乙种水果的进价为(x+5)元,由题意:用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.列出分式方程,解方程即可;
(2)设购进甲种水果m千克,则乙种水果(150﹣m)千克,利润为y元,由题意得y=﹣m+1650,再由甲种水果的重量不低于乙种水果重量的2倍,得m≥2(150﹣m),解得m≥100,然后由一次函数的性质即可得出结论.
解:(1)设甲种水果的进价为x元,则乙种水果的进价为(x+5)元,
由题意得:,
解得:x=20,
经检验:x=20是原方程的解,且符合题意,
则x+5=25,
答:甲种水果的进价为20元,则乙种水果的进价为25元;
(2)设购进甲种水果m千克,则乙种水果(150﹣m)千克,利润为y元,
由题意得:y=(30﹣20)m+(36﹣25)(150﹣m)=﹣m+1650,
∵甲种水果的重量不低于乙种水果重量的2倍,
∴m≥2(150﹣m),
解得:m≥100,
∵﹣1<0,则y随m的增大而减小,
∴当m=100时,y最大,最大值=﹣100+1650=1550,
则150﹣m=50,
答:购进甲种水果100千克,乙种水果50千克才能获得最大利润,最大利润为1550元.
【点评】本题考查了分式方程的应用、一元一次不等式的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找出数量关系,正确列出一元一次不等式.
23.【考点】平行四边形的判定与性质;勾股定理
【分析】利用平行四边形的性质求得EA=EC=2,EB=ED,利用勾股定理先后求得BC和BE,据此求解即可.
解:小明的解题过程不正确,从第③步开始错;
在平行四边形ABCD中,
∵AC=4,AB=5,
∴EA=ECAC4=2,EB=ED,
∵AC⊥BC,
∴,
∴BE,
∴BD=2EB=2.
【点评】本题考查了平行四边形的性质,勾股定理,关键是根据平行四边形的对角线相互平分解答.
24.【考点】因式分解﹣十字相乘法等;非负数的性质:偶次方;因式分解﹣分组分解法
【分析】(1)利用完全平方公式,加上一次项系数一半的平方即可;
(2)利用十字相乘法分解因式;
(3)利用配方法得到M=4(x)2,然后根据非负数的性质确定M的最小值.
解:(1)x2﹣8x+42=(x﹣4)2,
故答案为:16;
(2)x2﹣4xy﹣12y2=(x﹣6y)(x+2y);
(3)M=4x2+2x﹣1=4(x2x)﹣1
=4[x2x+()2﹣()2]﹣1
=4(x)2,
∵4(x)2≥0,
∴当x时,M有最小值.
【点评】本题考查了因式分解﹣十字相乘法等,熟练掌握因式分解的方法和配方法是解决问题的关键.
25.【考点】全等三角形的判定与性质;角平分线的性质;线段垂直平分线的性质
【分析】(1)利用线段的垂直平分线的性质证明即可;
(2)证明△AFD≌△AND(AAS),推出AF=AN,DF=DN,再证明△BFD≌△CND(HL),可得结论.
(1)证明:∵E为△ABC边BC的中点,DE⊥BC,
∴CD=BD;
(2)证明:过点D作DN⊥MC于点N,
∵AD为∠BAM角平分线,
∴∠DAN=∠DAF,
∵DN⊥MC,DF⊥AB,
∴∠AFD=∠AND,
在△AFD和△AND中,
,
∴△AFD≌△AND(AAS),
∴AF=AN,DF=DN,
∵∠BFD=∠CND=90°,
在Rt△BFD和Rt△CND中,
,
∴△BFD≌△CND(HL),
∴BF=CN=AC+AN=AC+AF.
【点评】本题考查了全等三角形的判定与性质,角平分线的性质,线段的垂直平分线的性质等知识,解题的关键是正确寻找全等三角形解决问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
