北师大版2024-2025学年八年级(下)期末数学模拟试卷2(含解析)
文档属性
| 名称 | 北师大版2024-2025学年八年级(下)期末数学模拟试卷2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:17:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2024-2025学年八年级(下)期末数学模拟试卷2
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共8小题,满分24分,每小题3分)
1.下列感冒胶囊的标识图中,属于中心对称图形的是( )
A. B. C. D.
2.若分式的值为0,则x的值是( )
A.2 B.1 C. D.
3.若一个三角形有两条边相等,且有一内角为60°,则这个三角形一定是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.钝角三角形
4.如图,矩形的长、宽分别为a、b,周长为12,面积为8,则a2b+ab2的值为( )
A.24 B.48 C.64 D.96
5.如图,点E是△ABC内一点,BE平分∠ABC,过点E作ED⊥BC于D,连EA.若ED=5,AB=10,则△AEB的面积是( )
A.20 B.30 C.25 D.15
6.若关于x的不等式组有且只有4个整数解,则a的取值范围是( )
A.4≤a≤5 B.4≤a<5 C.4<a≤5 D.4<a<5
7.在 ABCD中,若∠A=65°,则∠C的度数是( )
A.50° B.65° C.115° D.130°
8.如果关于x的方程1的解是正数,那么m的取值范围是( )
A.m>﹣1 B.m>﹣1且m≠0
C.m<﹣1 D.m<﹣1且m≠﹣2
二.填空题(共5小题,满分15分,每小题3分)
9.分解因式:﹣2ax2+4axy﹣2ay2= .
10.已知一个多边形的外角和与内角和的比为1:3,则这个多边形的边数为 .
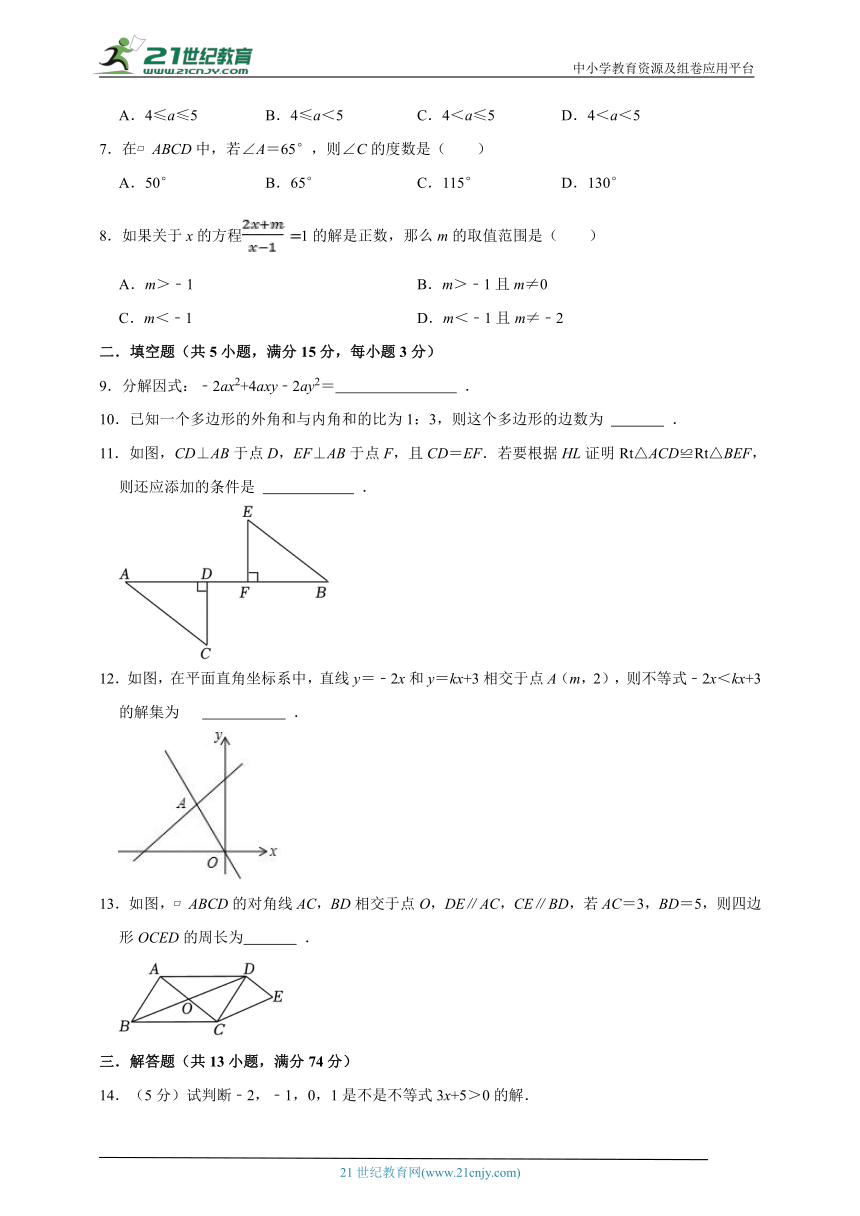
11.如图,CD⊥AB于点D,EF⊥AB于点F,且CD=EF.若要根据HL证明Rt△ACD≌Rt△BEF,则还应添加的条件是 .
12.如图,在平面直角坐标系中,直线y=﹣2x和y=kx+3相交于点A(m,2),则不等式﹣2x<kx+3的解集为 .
13.如图, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED的周长为 .
三.解答题(共13小题,满分74分)
14.(5分)试判断﹣2,﹣1,0,1是不是不等式3x+5>0的解.
15.(5分)解方程.
16.(5分)先化简,再求值:,其中a=2022.
17.(5分)在学习三角形的过程中,小明遇到这样一个问题:如图,在△ABC中,∠B=2∠C,把△ABC分成两个等腰三角形,并说明理由.聪明的小明经过思考后很快就有了思路:作线段AC的垂直平分线,利用线段垂直平分线的性质,得到两条相等线段,从而构造出等腰三角形,使问题得到了解决.
请根据小明的思路完成下面的作图并填空:
解:用直尺和圆规作AC的垂直平分线,分别交AC,BC于点D,E,连接AE.(不写作法,不下结论,只保留作图痕迹)
∵DE垂直平分线段AC,∴EA= .即△EAC是等腰三角形,∴∠EAC=∠C.
∵∠AEB=∠EAC+∠C,∴ =2∠C.∵∠B=2∠C,∴∠B=∠AEB,
∴AB= .即△ABE是等腰三角形.故△EAC和△ABE是等腰三角形.
18.(5分)如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF与BD交于点O.求证:OE=OF.
19.(5分)解不等式组:并把它的解集在数轴上表示出来.
20.(5分)如图,△ABC的中线AD,CE相交于点O.求证:.
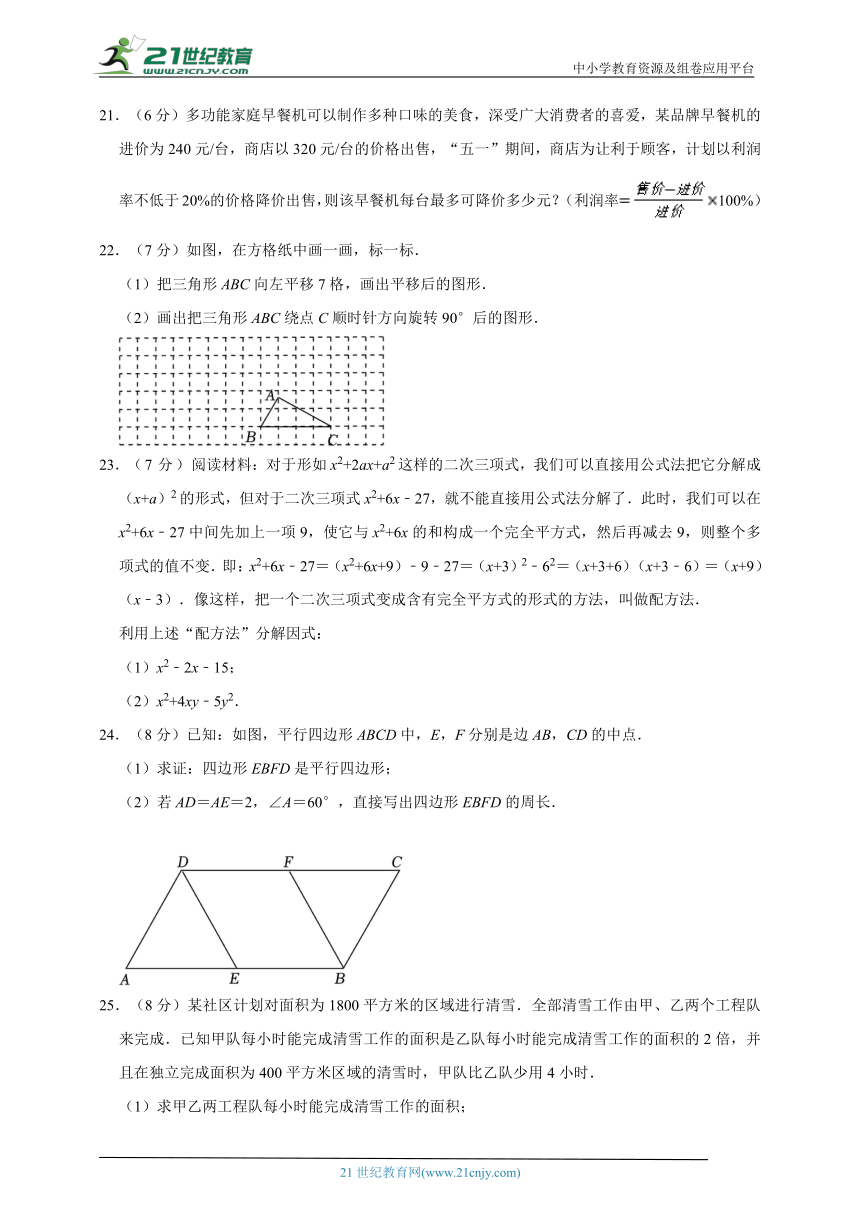
21.(6分)多功能家庭早餐机可以制作多种口味的美食,深受广大消费者的喜爱,某品牌早餐机的进价为240元/台,商店以320元/台的价格出售,“五一”期间,商店为让利于顾客,计划以利润率不低于20%的价格降价出售,则该早餐机每台最多可降价多少元?(利润率100%)
22.(7分)如图,在方格纸中画一画,标一标.
(1)把三角形ABC向左平移7格,画出平移后的图形.
(2)画出把三角形ABC绕点C顺时针方向旋转90°后的图形.
23.(7分)阅读材料:对于形如x2+2ax+a2这样的二次三项式,我们可以直接用公式法把它分解成(x+a)2的形式,但对于二次三项式x2+6x﹣27,就不能直接用公式法分解了.此时,我们可以在x2+6x﹣27中间先加上一项9,使它与x2+6x的和构成一个完全平方式,然后再减去9,则整个多项式的值不变.即:x2+6x﹣27=(x2+6x+9)﹣9﹣27=(x+3)2﹣62=(x+3+6)(x+3﹣6)=(x+9)(x﹣3).像这样,把一个二次三项式变成含有完全平方式的形式的方法,叫做配方法.
利用上述“配方法”分解因式:
(1)x2﹣2x﹣15;
(2)x2+4xy﹣5y2.
24.(8分)已知:如图,平行四边形ABCD中,E,F分别是边AB,CD的中点.
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,直接写出四边形EBFD的周长.
25.(8分)某社区计划对面积为1800平方米的区域进行清雪.全部清雪工作由甲、乙两个工程队来完成.已知甲队每小时能完成清雪工作的面积是乙队每小时能完成清雪工作的面积的2倍,并且在独立完成面积为400平方米区域的清雪时,甲队比乙队少用4小时.
(1)求甲乙两工程队每小时能完成清雪工作的面积;
(2)若甲队清雪的费用是6元/平方米,乙队清雪的费用是5元/平方米,如果施工总费用不超过1万元,那么乙工程队至少需要施工多少小时?
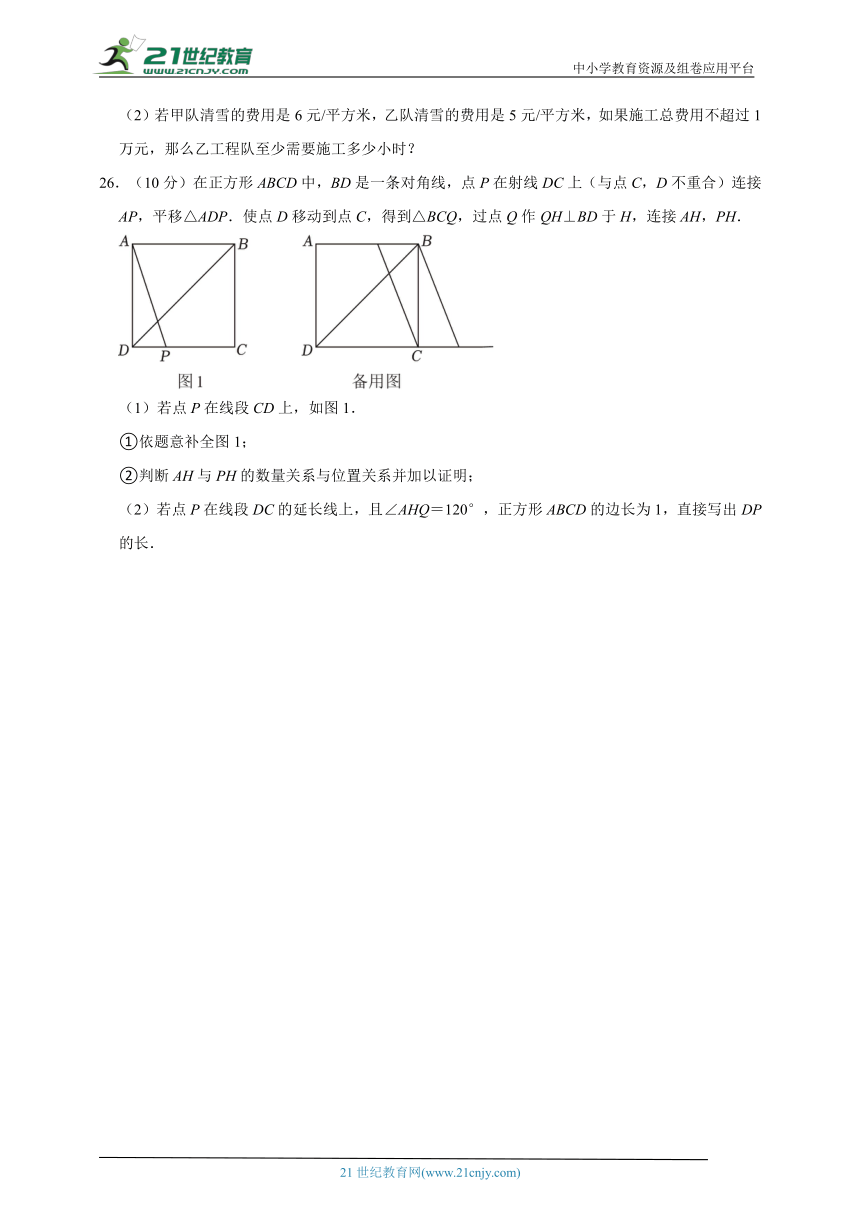
26.(10分)在正方形ABCD中,BD是一条对角线,点P在射线DC上(与点C,D不重合)连接AP,平移△ADP.使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.
(1)若点P在线段CD上,如图1.
①依题意补全图1;
②判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线段DC的延长线上,且∠AHQ=120°,正方形ABCD的边长为1,直接写出DP的长.
参考答案
一.选择题(共8小题,满分24分,每小题3分)
1.【考点】中心对称图形
【分析】根据中心对称图形的概念求解.在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.这个旋转点,就叫做中心对称点.
解:A、该图形不是中心对称图形,本选项不符合题意;
B、该图形不是中心对称图形,本选项不符合题意;
C、该图形不是中心对称图形,本选项不符合题意;
D、该图形是中心对称图形,本选项符合题意.
故选:D.
【点评】此题主要考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后两部分重合.
2.【考点】分式的值为零的条件
【分析】根据分式值为零的条件,可得:2x﹣1=0且3x+2≠0,据此求出x的值即可.
解:∵分式的值为0,
∴2x﹣1=0且3x+2≠0,
解得:x.
故选:C.
【点评】此题主要考查了分式值为零的条件,解答此题的关键是要明确:分式值为零的条件是分子等于零且分母不等于零,注意:“分母不为零”这个条件不能少.
3.【考点】等边三角形的判定
【分析】根据有一个角是60°的等腰三角形是等边三角形,即可得到答案.
解:∵一个三角形有两条边相等,
∴这个三角形是等腰三角形,
又∵这个三角形有一个内角为60°,
∴这个三角形一定为等边三角形.
故选:A.
【点评】本题考查了等边三角形的判定,解答本题的关键是熟练掌握等边三角形的判定定理1:三个角都相等的三角形是等边三角形;判定定理2:有一个角是60°的等腰三角形是等边三角形.
4.【考点】因式分解﹣提公因式法
【分析】直接利用矩形周长和面积公式得出a+b,ab,进而利用提取公因式法分解因式得出答案.
解:由题意得:2(a+b)=12,ab=8,
则a+b=6,
故a2b+ab2=ab(a+b)
=8×6
=48,
故选:B.
【点评】此题主要考查了提取公因式法以及矩形的性质应用,准确熟练地进行计算是解题的关键.
5.【考点】角平分线的性质
【分析】过E作EH⊥AB于H,由角平分线的性质得到EH=ED=5,而AB=10,由三角形面积公式即可求出△AEB的面积.
解:过E作EH⊥AB于H,
∵BE平分∠ABC,ED⊥BC于D,
∴EH=ED=5,
∵AB=10,
∴△AEB的面积AB EH10×5=25.
故选:C.
【点评】本题考查角平分线的性质,关键是由角平分线的性质得到EH=ED=5,
6.【考点】一元一次不等式组的整数解
【分析】先解不等式组,再利用不等式组只有4个整数解,即可得到关于a的不等式组,然后解关于a的不等式组即可.
解:不等式组整理得,
因为不等式组只有4个整数解,
所以﹣3≤2﹣a<﹣2,
所以4<a≤5.
故选:C.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
7.【考点】平行四边形的性质
【分析】由平行四边形的对角相等即可得出答案.
解:∵四边形ABCD是平行四边形,
∴∠C=∠A=65°,
故选:B.
【点评】本题考查了平行四边形的性质,熟记平行四边形的对角相等是解题的关键.
8.【考点】分式方程的解;解一元一次不等式
【分析】先去分母将分式方程化成整式方程,再求出方程的解x=﹣1﹣m,利用x>0和x≠1得出不等式组,解不等式组即可求出m的范围.
解:两边同时乘(x﹣1)得,
2x+m=x﹣1,
解得:x=﹣1﹣m,
又∵方程的解是正数,且x≠1,
∴,即,
解得:,
∴m的取值范围为:m<﹣1且m≠﹣2.
故答案为:D.
【点评】本题主要考查了分式方程的解,一元一次不等式,正确求得分式方程的解并考虑产生增根的情形是解题的关键.
二.填空题(共5小题,满分15分,每小题3分)
9.【考点】提公因式法与公式法的综合运用
【分析】先提公因式,再利用完全平方公式继续分解即可解答.
解:﹣2ax2+4axy﹣2ay2
=﹣2a(x2﹣2xy+y2)
=﹣2a(x﹣y)2,
故答案为:﹣2a(x﹣y)2.
【点评】本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
10.【考点】多边形内角与外角
【分析】根据多边形的外角和为360°,由内角和和外角和的比,即可得到多边形的内角和,根据公式求出多边形的边数即可.
解:∵多边形的外角和为360°,外角和:内角和=1:3,
∴多边形的内角和为360°×3=1080°,
设多边形的边数为n,
∴180°(n﹣2)=1080°,
∴n=8,
故答案为:8.
【点评】本题考查了多边形内角与外角,理解多边形的外角和是360度,外角和不随边数的变化而变化是解题的关键.
11.【考点】直角三角形全等的判定;全等三角形的判定
【分析】添加AC=BE,根据HL即可证明Rt△ACD≌Rt△BEF.
解:添加AC=BE,理由如下:
∵CD⊥AB,EF⊥AB,
∴∠ADC=∠BFE=90°,
在Rt△ACD和Rt△BEF中,
,
∴Rt△ACD≌Rt△BEF(HL),
故答案为:AC=BE.
【点评】本题考查了直角三角形全等的判定,熟练掌握HL是解题的关键.
12.【考点】一次函数与一元一次不等式;两条直线相交或平行问题
【分析】将点A坐标代入正比例函数解析式,求出m的值,进而求解.
解:将(m,2)代入y=﹣2x得2=﹣2m,
解得m=﹣1,
∴x>﹣1时,直线y=﹣2x在直线kx+3下方,
∴不等式﹣2x<kx+3的解集为x>﹣1,
故答案为:x>﹣1.
【点评】本题考查一次函数的性质,解题关键是掌握一次函数与方程及不等式的关系.
13.【考点】平行四边形的性质
【分析】根据平行四边形对角线互相平分得出OC、OD的长,再证明四边形OCED是平行四边形即可得出结果.
解:∵ ABCD的对角线AC,BD相交于点O,AC=3,BD=5,
∴,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED的周长,
故答案为:8.
【点评】本题考查了平行四边形的判定与性质,解答本题的关键是熟练掌握平行四边形的性质.
三.解答题(共13小题,满分74分)
14.【考点】解一元一次不等式
【分析】求出x的取值范围,从而判断这4个数中哪些是不等式的解即可.
解:由3x+5>0得:x,
∵﹣2,﹣1,0,1,
∴﹣2不是不等式3x+5>0的解,﹣1,0,1是不等式3x+5>0的解.
【点评】本题考查一元一次不等式的解集,求出已知一元一次不等式的解集是解题的关键.
15.【考点】解分式方程
【分析】根据解分式方程的方法,先将分式方程转化为整式方程,解分式方程求出x的值,最后检验即可.
解:,
方程两边同时乘x﹣1,得x+2=3(x﹣1),
去括号,得x+2=3x﹣3,
解得:x,
检验:把代入x﹣1≠0,
∴分式方程的解为.
【点评】本题考查了解分式方程,熟练掌握解分式方程的方法是解题的关键.
16.【考点】分式的化简求值
【分析】先利用异分母分式加减法法则计算括号里,再算括号外,然后把a的值代入化简后的式子,进行计算即可解答.
解:
,
当a=2022时,原式.
【点评】本题考查了分式的化简求值,准确熟练地进行计算是解题的关键.
17.【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的判定与性质
【分析】用直尺和圆规作AC的垂直平分线,分别交AC,BC于点D,E,连接AE即可,根据线段垂直平分线的性质以、三角形的外角性质以及等角对等边即可判定△EAC和△ABE是等腰三角形.
解:作图如下,△EAC和△ABE是所求作的三角形,
∵DE垂直平分线段AC,
∴EA=EC.即△EAC是等腰三角形,
∴∠EAC=∠C.
∵∠AEB=∠EAC+∠C,
∴∠AEB=2∠C.
∵∠B=2∠C,
∴∠B=∠AEB,
∴AB=AE.即△ABE是等腰三角形.故△EAC和△ABE是等腰三角形.
故答案为:EC,∠AEB,AE.
【点评】本题主要考查了等腰三角形的判定及性质,线段垂直平分线的性质,三角形的外角性质,熟练掌握相关性质是解题的关键.
18.【考点】平行四边形的性质;全等三角形的判定与性质
【分析】根据平行四边形的性质可得AD=BC,AD∥BC,由对顶角相等可得∠EOD=∠FOB,再根据平行线的性质可得∠OBF=∠ODE,从而可证△BOF≌△DOE(AAS),即可得出结论.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠OBF=∠ODE,
∵AE=CF,
∴DE=BF,
∵∠EOD=∠FOB,
在△BOF和△DOE中,
,
∴△BOF≌△DOE(AAS),
∴OE=OF.
【点评】本题考查平行四边形的性质、平行线的性质、对顶角相等、全等三角形的判定与性质,熟练掌握平行四边形的性质和全等三角形的判定与性质证得△BOF≌△DOE是解题的关键.
19.【考点】解一元一次不等式组;在数轴上表示不等式的解集
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集,并把解集表示在数轴上即可求解.
解:,
由①得:x<3,由②得:x>1,
∴原不等式的解集为1<x<3.
解集在数轴上表示如图,
【点评】本题考查了解一元一次不等式组,在数轴上表示不等式的解集,正确的计算是解题的关键.
20.【考点】三角形的重心;三角形中位线定理;平行四边形的判定与性质
【分析】取AO的中点M,OC的中点N,连接DE,EM,MN,DN,根据三角形的中位线定理得到MN∥AC,MNAC,DE∥AC,DEAC,推出四边形DEMN是平行四边形,根据平行四边形的性质得到OD=OM,于是得到ODAD.
证明:取AO的中点M,OC的中点N,连接DE,EM,MN,DN,
∴OM=AMAO,ON=CN,
∴MN是△AOC的中位线,
∴MN∥AC,MNAC,
∵△ABC的中线AD,CE相交于点O,
∴DE是△ABC的中位线,
∴DE∥AC,DEAC,
∴DE=MN,DE∥MN,
∴四边形DEMN是平行四边形,
∴OD=OM,
∴ODAD.
【点评】本题考查了三角形的重心,平行四边形的判定和性质,三角形的中位线定理,正确地作出辅助线是解题的关键.
21.【考点】一元一次不等式的应用
【分析】设该早餐机每台可降价x元,根据计划以利润率不低于20%的价格降价出售,列出一元一次不等式,解不等式即可.
解:设该早餐机每台可降价x元,
根据题意得:320﹣x﹣240≥240×20%,
解得:x≤32,
∴x的最大值为32,
答:该早餐机每台最多可降价32元.
【点评】本题考查了一元一次不等式的应用,找出数量关系,正确列出一元一次不等式是解题的关键.
22.【考点】作图﹣旋转变换;作图﹣平移变换
【分析】(1)把原三角形的每个顶点都向左平移7格,然后顺次连线.
(2)把原三角形的每条边都绕C点顺时针旋转90°,画出旋转后的图形.
解:(1)如图,△A'B'C'为所求图形;
(2)如图,△CDE为所求图形.
【点评】本题考查了作图﹣旋转变换,平移变换,掌握图形的作法是解决本题的关键.
23.【考点】因式分解﹣十字相乘法等;提公因式法与公式法的综合运用
【分析】(1)将原式变形为x2﹣2x+1﹣1﹣15,再利用完全平方公式和平方差公式分解即可;
(2)将原式变形为x2+4xy+4y2﹣4y2﹣5y2,再利用完全平方公式和平方差公式分解即可.
解:(1)x2﹣2x﹣15
=x2﹣2x+1﹣1﹣15
=(x﹣1)2﹣42
=(x﹣1+4)(x﹣1﹣4)
=(x+3)(x﹣5);
(2)x2+4xy﹣5y2
=x2+4xy+4y2﹣4y2﹣5y2
=(x+2y)2﹣(3y)2
=(x+2y+3y)(x+2y﹣3y)
=(x+5y)(x﹣y).
【点评】本题考查了因式分解,解题的关键是掌握完全平方公式和平方差公式.
24.【考点】平行四边形的判定与性质;等边三角形的性质
【分析】(1)在 ABCD中,AB=CD,AB∥CD,又E、F分别是边AB、CD的中点,所以BE=CF,因此四边形EBFD是平行四边形
(2)由AD=AE=2,∠A=60°知△ADE是等边三角形,又E、F分别是边AB、CD的中点,四边形EBFD是平行四边形,所以EB=BF=FD=DE=2,四边形EBFD是平行四边形的周长是2+2+2+2=8.
(1)证明:在 ABCD中,
AB=CD,AB∥CD.
∵E、F分别是AB、CD的中点,
∴.
∴BE=DF.
∴四边形EBFD是平行四边形;
(2)解:∵AD=AE,∠A=60°,
∴△ADE是等边三角形.
∴DE=AD=2,
又∵BE=AE=2,
由(1)知四边形EBFD是平行四边形,
∴四边形EBFD的周长=2(BE+DE)=8.
【点评】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.
25.【考点】分式方程的应用;一元一次不等式的应用
【分析】(1)设乙工程队每小时能完成清雪的面积为x平方米,则甲工程队每小时能完成清雪的面积为2x平方米,根据“在独立完成面积为400平方米区域的清雪时,甲队比乙队少用4小时”,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设乙工程队施工y小时,根据施工总费用不超过1万元列不等式求解即可.
解:(1)设乙工程队每小时能清雪x平方米,则甲工程队每小时能清雪2x平方米,
,
解得:x=50,
经检验x=50 符合题意且是方程的解,
2x=100(平方米),
答:甲每小时清雪100平方米,乙每小时清雪50平方米;
(2)设乙工程队施工y小时,
6×(1800﹣50y)+5×50y≤10000,
解得:y≥16,
答:乙队至少施工16小时.
【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
26.【考点】四边形综合题
【分析】(1)①根据题意画出图形即可;
②连接CH,先根据正方形的性质得出△DHQ是等腰直角三角形,再由SAS定理得出△HDP≌△HQC,故PH=CH,∠HPC=∠HCP,由正方形的性质即可得出结论;
(2)同(1)②的可证AH=PH,AH⊥PH,得出∠HPA=45°,推导出∠APD=30°,再由三角函数即可求解.
解:(1)①如图1;
②AH=PH,AH⊥PH.理由如下:
如图1,连接CH,
∵四边形ABCD是正方形,
∴∠BDC=45°,
又QH⊥BD,
∴△DHQ是等腰直角三角形,
由平移的性质可知DP=CQ,
在△HDP和△HQC中,
,
∴△HDP≌△HQC(SAS),
∴HP=HC,∠DHP=∠QHC,
根据正方形是轴对称图形得到HA=HC,∠AHD=∠CHD,
∴AH=PH,AH⊥PH;
(2)如图2,点P在线段DC的延长线上,点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH,CH,作HR⊥PC于点R,
同(1)②可证:AH=PH,AH⊥PH,
∴∠HPA=45°,
∵∠AHQ=120°,
∴∠AHB=∠CHB=30°,
∴∠QHP=∠CHB=∠CHP=30°,
∴∠CPH=75°,
∴∠APD=30°,
在Rt△APD中,AD=1,
∴PD=AD tan60°=tan60°.
【点评】此题是四边形综合题,主要考查了正方形的性质、图形平移的性质、全等三角形的判定与性质等知识,难度适中,解决本题的关键是熟记全等三角形的性质定理和判定定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版2024-2025学年八年级(下)期末数学模拟试卷2
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共8小题,满分24分,每小题3分)
1.下列感冒胶囊的标识图中,属于中心对称图形的是( )
A. B. C. D.
2.若分式的值为0,则x的值是( )
A.2 B.1 C. D.
3.若一个三角形有两条边相等,且有一内角为60°,则这个三角形一定是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.钝角三角形
4.如图,矩形的长、宽分别为a、b,周长为12,面积为8,则a2b+ab2的值为( )
A.24 B.48 C.64 D.96
5.如图,点E是△ABC内一点,BE平分∠ABC,过点E作ED⊥BC于D,连EA.若ED=5,AB=10,则△AEB的面积是( )
A.20 B.30 C.25 D.15
6.若关于x的不等式组有且只有4个整数解,则a的取值范围是( )
A.4≤a≤5 B.4≤a<5 C.4<a≤5 D.4<a<5
7.在 ABCD中,若∠A=65°,则∠C的度数是( )
A.50° B.65° C.115° D.130°
8.如果关于x的方程1的解是正数,那么m的取值范围是( )
A.m>﹣1 B.m>﹣1且m≠0
C.m<﹣1 D.m<﹣1且m≠﹣2
二.填空题(共5小题,满分15分,每小题3分)
9.分解因式:﹣2ax2+4axy﹣2ay2= .
10.已知一个多边形的外角和与内角和的比为1:3,则这个多边形的边数为 .
11.如图,CD⊥AB于点D,EF⊥AB于点F,且CD=EF.若要根据HL证明Rt△ACD≌Rt△BEF,则还应添加的条件是 .
12.如图,在平面直角坐标系中,直线y=﹣2x和y=kx+3相交于点A(m,2),则不等式﹣2x<kx+3的解集为 .
13.如图, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED的周长为 .
三.解答题(共13小题,满分74分)
14.(5分)试判断﹣2,﹣1,0,1是不是不等式3x+5>0的解.
15.(5分)解方程.
16.(5分)先化简,再求值:,其中a=2022.
17.(5分)在学习三角形的过程中,小明遇到这样一个问题:如图,在△ABC中,∠B=2∠C,把△ABC分成两个等腰三角形,并说明理由.聪明的小明经过思考后很快就有了思路:作线段AC的垂直平分线,利用线段垂直平分线的性质,得到两条相等线段,从而构造出等腰三角形,使问题得到了解决.
请根据小明的思路完成下面的作图并填空:
解:用直尺和圆规作AC的垂直平分线,分别交AC,BC于点D,E,连接AE.(不写作法,不下结论,只保留作图痕迹)
∵DE垂直平分线段AC,∴EA= .即△EAC是等腰三角形,∴∠EAC=∠C.
∵∠AEB=∠EAC+∠C,∴ =2∠C.∵∠B=2∠C,∴∠B=∠AEB,
∴AB= .即△ABE是等腰三角形.故△EAC和△ABE是等腰三角形.
18.(5分)如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF与BD交于点O.求证:OE=OF.
19.(5分)解不等式组:并把它的解集在数轴上表示出来.
20.(5分)如图,△ABC的中线AD,CE相交于点O.求证:.
21.(6分)多功能家庭早餐机可以制作多种口味的美食,深受广大消费者的喜爱,某品牌早餐机的进价为240元/台,商店以320元/台的价格出售,“五一”期间,商店为让利于顾客,计划以利润率不低于20%的价格降价出售,则该早餐机每台最多可降价多少元?(利润率100%)
22.(7分)如图,在方格纸中画一画,标一标.
(1)把三角形ABC向左平移7格,画出平移后的图形.
(2)画出把三角形ABC绕点C顺时针方向旋转90°后的图形.
23.(7分)阅读材料:对于形如x2+2ax+a2这样的二次三项式,我们可以直接用公式法把它分解成(x+a)2的形式,但对于二次三项式x2+6x﹣27,就不能直接用公式法分解了.此时,我们可以在x2+6x﹣27中间先加上一项9,使它与x2+6x的和构成一个完全平方式,然后再减去9,则整个多项式的值不变.即:x2+6x﹣27=(x2+6x+9)﹣9﹣27=(x+3)2﹣62=(x+3+6)(x+3﹣6)=(x+9)(x﹣3).像这样,把一个二次三项式变成含有完全平方式的形式的方法,叫做配方法.
利用上述“配方法”分解因式:
(1)x2﹣2x﹣15;
(2)x2+4xy﹣5y2.
24.(8分)已知:如图,平行四边形ABCD中,E,F分别是边AB,CD的中点.
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,直接写出四边形EBFD的周长.
25.(8分)某社区计划对面积为1800平方米的区域进行清雪.全部清雪工作由甲、乙两个工程队来完成.已知甲队每小时能完成清雪工作的面积是乙队每小时能完成清雪工作的面积的2倍,并且在独立完成面积为400平方米区域的清雪时,甲队比乙队少用4小时.
(1)求甲乙两工程队每小时能完成清雪工作的面积;
(2)若甲队清雪的费用是6元/平方米,乙队清雪的费用是5元/平方米,如果施工总费用不超过1万元,那么乙工程队至少需要施工多少小时?
26.(10分)在正方形ABCD中,BD是一条对角线,点P在射线DC上(与点C,D不重合)连接AP,平移△ADP.使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.
(1)若点P在线段CD上,如图1.
①依题意补全图1;
②判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线段DC的延长线上,且∠AHQ=120°,正方形ABCD的边长为1,直接写出DP的长.
参考答案
一.选择题(共8小题,满分24分,每小题3分)
1.【考点】中心对称图形
【分析】根据中心对称图形的概念求解.在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.这个旋转点,就叫做中心对称点.
解:A、该图形不是中心对称图形,本选项不符合题意;
B、该图形不是中心对称图形,本选项不符合题意;
C、该图形不是中心对称图形,本选项不符合题意;
D、该图形是中心对称图形,本选项符合题意.
故选:D.
【点评】此题主要考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后两部分重合.
2.【考点】分式的值为零的条件
【分析】根据分式值为零的条件,可得:2x﹣1=0且3x+2≠0,据此求出x的值即可.
解:∵分式的值为0,
∴2x﹣1=0且3x+2≠0,
解得:x.
故选:C.
【点评】此题主要考查了分式值为零的条件,解答此题的关键是要明确:分式值为零的条件是分子等于零且分母不等于零,注意:“分母不为零”这个条件不能少.
3.【考点】等边三角形的判定
【分析】根据有一个角是60°的等腰三角形是等边三角形,即可得到答案.
解:∵一个三角形有两条边相等,
∴这个三角形是等腰三角形,
又∵这个三角形有一个内角为60°,
∴这个三角形一定为等边三角形.
故选:A.
【点评】本题考查了等边三角形的判定,解答本题的关键是熟练掌握等边三角形的判定定理1:三个角都相等的三角形是等边三角形;判定定理2:有一个角是60°的等腰三角形是等边三角形.
4.【考点】因式分解﹣提公因式法
【分析】直接利用矩形周长和面积公式得出a+b,ab,进而利用提取公因式法分解因式得出答案.
解:由题意得:2(a+b)=12,ab=8,
则a+b=6,
故a2b+ab2=ab(a+b)
=8×6
=48,
故选:B.
【点评】此题主要考查了提取公因式法以及矩形的性质应用,准确熟练地进行计算是解题的关键.
5.【考点】角平分线的性质
【分析】过E作EH⊥AB于H,由角平分线的性质得到EH=ED=5,而AB=10,由三角形面积公式即可求出△AEB的面积.
解:过E作EH⊥AB于H,
∵BE平分∠ABC,ED⊥BC于D,
∴EH=ED=5,
∵AB=10,
∴△AEB的面积AB EH10×5=25.
故选:C.
【点评】本题考查角平分线的性质,关键是由角平分线的性质得到EH=ED=5,
6.【考点】一元一次不等式组的整数解
【分析】先解不等式组,再利用不等式组只有4个整数解,即可得到关于a的不等式组,然后解关于a的不等式组即可.
解:不等式组整理得,
因为不等式组只有4个整数解,
所以﹣3≤2﹣a<﹣2,
所以4<a≤5.
故选:C.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
7.【考点】平行四边形的性质
【分析】由平行四边形的对角相等即可得出答案.
解:∵四边形ABCD是平行四边形,
∴∠C=∠A=65°,
故选:B.
【点评】本题考查了平行四边形的性质,熟记平行四边形的对角相等是解题的关键.
8.【考点】分式方程的解;解一元一次不等式
【分析】先去分母将分式方程化成整式方程,再求出方程的解x=﹣1﹣m,利用x>0和x≠1得出不等式组,解不等式组即可求出m的范围.
解:两边同时乘(x﹣1)得,
2x+m=x﹣1,
解得:x=﹣1﹣m,
又∵方程的解是正数,且x≠1,
∴,即,
解得:,
∴m的取值范围为:m<﹣1且m≠﹣2.
故答案为:D.
【点评】本题主要考查了分式方程的解,一元一次不等式,正确求得分式方程的解并考虑产生增根的情形是解题的关键.
二.填空题(共5小题,满分15分,每小题3分)
9.【考点】提公因式法与公式法的综合运用
【分析】先提公因式,再利用完全平方公式继续分解即可解答.
解:﹣2ax2+4axy﹣2ay2
=﹣2a(x2﹣2xy+y2)
=﹣2a(x﹣y)2,
故答案为:﹣2a(x﹣y)2.
【点评】本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
10.【考点】多边形内角与外角
【分析】根据多边形的外角和为360°,由内角和和外角和的比,即可得到多边形的内角和,根据公式求出多边形的边数即可.
解:∵多边形的外角和为360°,外角和:内角和=1:3,
∴多边形的内角和为360°×3=1080°,
设多边形的边数为n,
∴180°(n﹣2)=1080°,
∴n=8,
故答案为:8.
【点评】本题考查了多边形内角与外角,理解多边形的外角和是360度,外角和不随边数的变化而变化是解题的关键.
11.【考点】直角三角形全等的判定;全等三角形的判定
【分析】添加AC=BE,根据HL即可证明Rt△ACD≌Rt△BEF.
解:添加AC=BE,理由如下:
∵CD⊥AB,EF⊥AB,
∴∠ADC=∠BFE=90°,
在Rt△ACD和Rt△BEF中,
,
∴Rt△ACD≌Rt△BEF(HL),
故答案为:AC=BE.
【点评】本题考查了直角三角形全等的判定,熟练掌握HL是解题的关键.
12.【考点】一次函数与一元一次不等式;两条直线相交或平行问题
【分析】将点A坐标代入正比例函数解析式,求出m的值,进而求解.
解:将(m,2)代入y=﹣2x得2=﹣2m,
解得m=﹣1,
∴x>﹣1时,直线y=﹣2x在直线kx+3下方,
∴不等式﹣2x<kx+3的解集为x>﹣1,
故答案为:x>﹣1.
【点评】本题考查一次函数的性质,解题关键是掌握一次函数与方程及不等式的关系.
13.【考点】平行四边形的性质
【分析】根据平行四边形对角线互相平分得出OC、OD的长,再证明四边形OCED是平行四边形即可得出结果.
解:∵ ABCD的对角线AC,BD相交于点O,AC=3,BD=5,
∴,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED的周长,
故答案为:8.
【点评】本题考查了平行四边形的判定与性质,解答本题的关键是熟练掌握平行四边形的性质.
三.解答题(共13小题,满分74分)
14.【考点】解一元一次不等式
【分析】求出x的取值范围,从而判断这4个数中哪些是不等式的解即可.
解:由3x+5>0得:x,
∵﹣2,﹣1,0,1,
∴﹣2不是不等式3x+5>0的解,﹣1,0,1是不等式3x+5>0的解.
【点评】本题考查一元一次不等式的解集,求出已知一元一次不等式的解集是解题的关键.
15.【考点】解分式方程
【分析】根据解分式方程的方法,先将分式方程转化为整式方程,解分式方程求出x的值,最后检验即可.
解:,
方程两边同时乘x﹣1,得x+2=3(x﹣1),
去括号,得x+2=3x﹣3,
解得:x,
检验:把代入x﹣1≠0,
∴分式方程的解为.
【点评】本题考查了解分式方程,熟练掌握解分式方程的方法是解题的关键.
16.【考点】分式的化简求值
【分析】先利用异分母分式加减法法则计算括号里,再算括号外,然后把a的值代入化简后的式子,进行计算即可解答.
解:
,
当a=2022时,原式.
【点评】本题考查了分式的化简求值,准确熟练地进行计算是解题的关键.
17.【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的判定与性质
【分析】用直尺和圆规作AC的垂直平分线,分别交AC,BC于点D,E,连接AE即可,根据线段垂直平分线的性质以、三角形的外角性质以及等角对等边即可判定△EAC和△ABE是等腰三角形.
解:作图如下,△EAC和△ABE是所求作的三角形,
∵DE垂直平分线段AC,
∴EA=EC.即△EAC是等腰三角形,
∴∠EAC=∠C.
∵∠AEB=∠EAC+∠C,
∴∠AEB=2∠C.
∵∠B=2∠C,
∴∠B=∠AEB,
∴AB=AE.即△ABE是等腰三角形.故△EAC和△ABE是等腰三角形.
故答案为:EC,∠AEB,AE.
【点评】本题主要考查了等腰三角形的判定及性质,线段垂直平分线的性质,三角形的外角性质,熟练掌握相关性质是解题的关键.
18.【考点】平行四边形的性质;全等三角形的判定与性质
【分析】根据平行四边形的性质可得AD=BC,AD∥BC,由对顶角相等可得∠EOD=∠FOB,再根据平行线的性质可得∠OBF=∠ODE,从而可证△BOF≌△DOE(AAS),即可得出结论.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠OBF=∠ODE,
∵AE=CF,
∴DE=BF,
∵∠EOD=∠FOB,
在△BOF和△DOE中,
,
∴△BOF≌△DOE(AAS),
∴OE=OF.
【点评】本题考查平行四边形的性质、平行线的性质、对顶角相等、全等三角形的判定与性质,熟练掌握平行四边形的性质和全等三角形的判定与性质证得△BOF≌△DOE是解题的关键.
19.【考点】解一元一次不等式组;在数轴上表示不等式的解集
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集,并把解集表示在数轴上即可求解.
解:,
由①得:x<3,由②得:x>1,
∴原不等式的解集为1<x<3.
解集在数轴上表示如图,
【点评】本题考查了解一元一次不等式组,在数轴上表示不等式的解集,正确的计算是解题的关键.
20.【考点】三角形的重心;三角形中位线定理;平行四边形的判定与性质
【分析】取AO的中点M,OC的中点N,连接DE,EM,MN,DN,根据三角形的中位线定理得到MN∥AC,MNAC,DE∥AC,DEAC,推出四边形DEMN是平行四边形,根据平行四边形的性质得到OD=OM,于是得到ODAD.
证明:取AO的中点M,OC的中点N,连接DE,EM,MN,DN,
∴OM=AMAO,ON=CN,
∴MN是△AOC的中位线,
∴MN∥AC,MNAC,
∵△ABC的中线AD,CE相交于点O,
∴DE是△ABC的中位线,
∴DE∥AC,DEAC,
∴DE=MN,DE∥MN,
∴四边形DEMN是平行四边形,
∴OD=OM,
∴ODAD.
【点评】本题考查了三角形的重心,平行四边形的判定和性质,三角形的中位线定理,正确地作出辅助线是解题的关键.
21.【考点】一元一次不等式的应用
【分析】设该早餐机每台可降价x元,根据计划以利润率不低于20%的价格降价出售,列出一元一次不等式,解不等式即可.
解:设该早餐机每台可降价x元,
根据题意得:320﹣x﹣240≥240×20%,
解得:x≤32,
∴x的最大值为32,
答:该早餐机每台最多可降价32元.
【点评】本题考查了一元一次不等式的应用,找出数量关系,正确列出一元一次不等式是解题的关键.
22.【考点】作图﹣旋转变换;作图﹣平移变换
【分析】(1)把原三角形的每个顶点都向左平移7格,然后顺次连线.
(2)把原三角形的每条边都绕C点顺时针旋转90°,画出旋转后的图形.
解:(1)如图,△A'B'C'为所求图形;
(2)如图,△CDE为所求图形.
【点评】本题考查了作图﹣旋转变换,平移变换,掌握图形的作法是解决本题的关键.
23.【考点】因式分解﹣十字相乘法等;提公因式法与公式法的综合运用
【分析】(1)将原式变形为x2﹣2x+1﹣1﹣15,再利用完全平方公式和平方差公式分解即可;
(2)将原式变形为x2+4xy+4y2﹣4y2﹣5y2,再利用完全平方公式和平方差公式分解即可.
解:(1)x2﹣2x﹣15
=x2﹣2x+1﹣1﹣15
=(x﹣1)2﹣42
=(x﹣1+4)(x﹣1﹣4)
=(x+3)(x﹣5);
(2)x2+4xy﹣5y2
=x2+4xy+4y2﹣4y2﹣5y2
=(x+2y)2﹣(3y)2
=(x+2y+3y)(x+2y﹣3y)
=(x+5y)(x﹣y).
【点评】本题考查了因式分解,解题的关键是掌握完全平方公式和平方差公式.
24.【考点】平行四边形的判定与性质;等边三角形的性质
【分析】(1)在 ABCD中,AB=CD,AB∥CD,又E、F分别是边AB、CD的中点,所以BE=CF,因此四边形EBFD是平行四边形
(2)由AD=AE=2,∠A=60°知△ADE是等边三角形,又E、F分别是边AB、CD的中点,四边形EBFD是平行四边形,所以EB=BF=FD=DE=2,四边形EBFD是平行四边形的周长是2+2+2+2=8.
(1)证明:在 ABCD中,
AB=CD,AB∥CD.
∵E、F分别是AB、CD的中点,
∴.
∴BE=DF.
∴四边形EBFD是平行四边形;
(2)解:∵AD=AE,∠A=60°,
∴△ADE是等边三角形.
∴DE=AD=2,
又∵BE=AE=2,
由(1)知四边形EBFD是平行四边形,
∴四边形EBFD的周长=2(BE+DE)=8.
【点评】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.
25.【考点】分式方程的应用;一元一次不等式的应用
【分析】(1)设乙工程队每小时能完成清雪的面积为x平方米,则甲工程队每小时能完成清雪的面积为2x平方米,根据“在独立完成面积为400平方米区域的清雪时,甲队比乙队少用4小时”,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设乙工程队施工y小时,根据施工总费用不超过1万元列不等式求解即可.
解:(1)设乙工程队每小时能清雪x平方米,则甲工程队每小时能清雪2x平方米,
,
解得:x=50,
经检验x=50 符合题意且是方程的解,
2x=100(平方米),
答:甲每小时清雪100平方米,乙每小时清雪50平方米;
(2)设乙工程队施工y小时,
6×(1800﹣50y)+5×50y≤10000,
解得:y≥16,
答:乙队至少施工16小时.
【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
26.【考点】四边形综合题
【分析】(1)①根据题意画出图形即可;
②连接CH,先根据正方形的性质得出△DHQ是等腰直角三角形,再由SAS定理得出△HDP≌△HQC,故PH=CH,∠HPC=∠HCP,由正方形的性质即可得出结论;
(2)同(1)②的可证AH=PH,AH⊥PH,得出∠HPA=45°,推导出∠APD=30°,再由三角函数即可求解.
解:(1)①如图1;
②AH=PH,AH⊥PH.理由如下:
如图1,连接CH,
∵四边形ABCD是正方形,
∴∠BDC=45°,
又QH⊥BD,
∴△DHQ是等腰直角三角形,
由平移的性质可知DP=CQ,
在△HDP和△HQC中,
,
∴△HDP≌△HQC(SAS),
∴HP=HC,∠DHP=∠QHC,
根据正方形是轴对称图形得到HA=HC,∠AHD=∠CHD,
∴AH=PH,AH⊥PH;
(2)如图2,点P在线段DC的延长线上,点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH,CH,作HR⊥PC于点R,
同(1)②可证:AH=PH,AH⊥PH,
∴∠HPA=45°,
∵∠AHQ=120°,
∴∠AHB=∠CHB=30°,
∴∠QHP=∠CHB=∠CHP=30°,
∴∠CPH=75°,
∴∠APD=30°,
在Rt△APD中,AD=1,
∴PD=AD tan60°=tan60°.
【点评】此题是四边形综合题,主要考查了正方形的性质、图形平移的性质、全等三角形的判定与性质等知识,难度适中,解决本题的关键是熟记全等三角形的性质定理和判定定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
