数学:23.2中心对称(第4课时)课件(人教新课标九年级上)
文档属性
| 名称 | 数学:23.2中心对称(第4课时)课件(人教新课标九年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-15 20:29:00 | ||
图片预览




文档简介
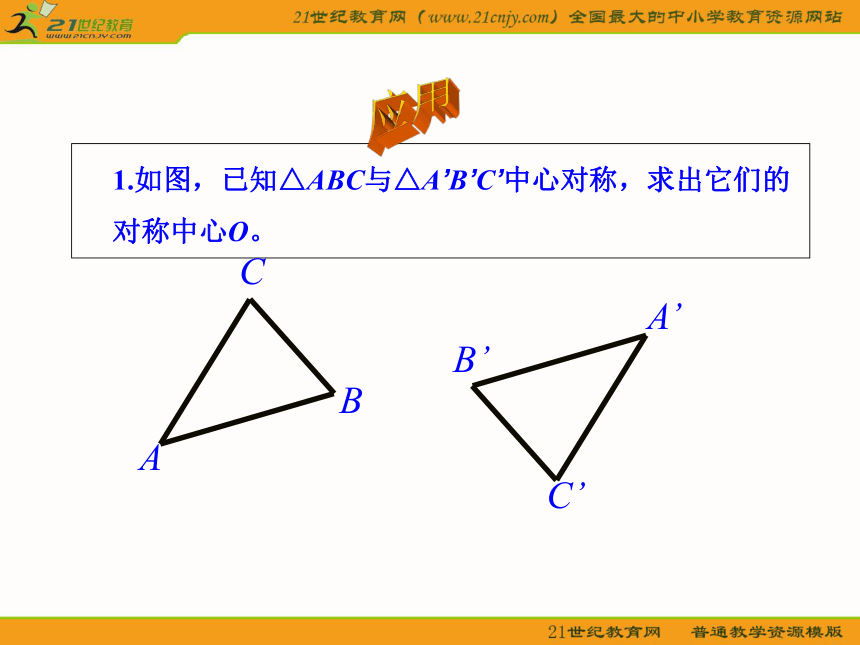
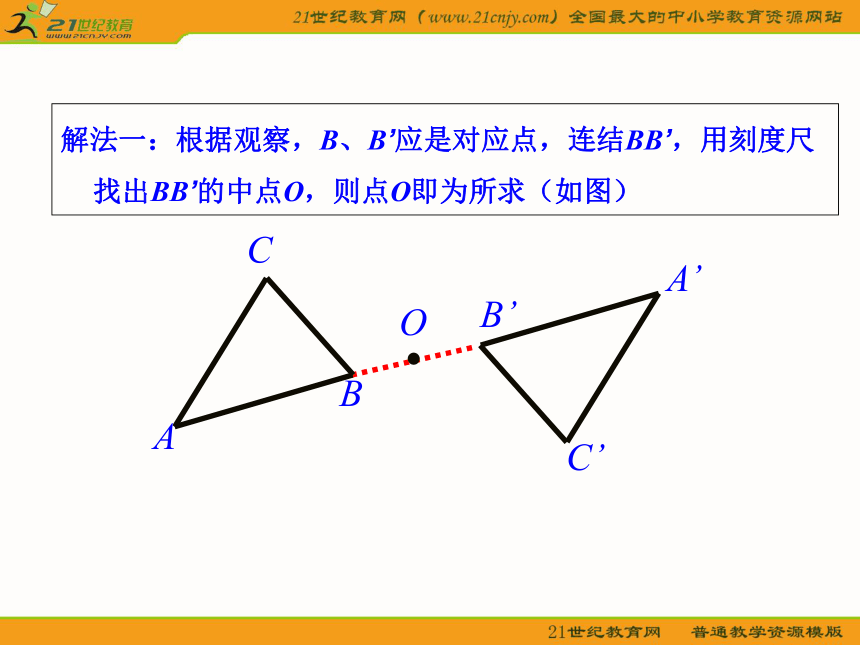
课件18张PPT。23.2 中心对称重点,难点复习 1.如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。应用解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)OO解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
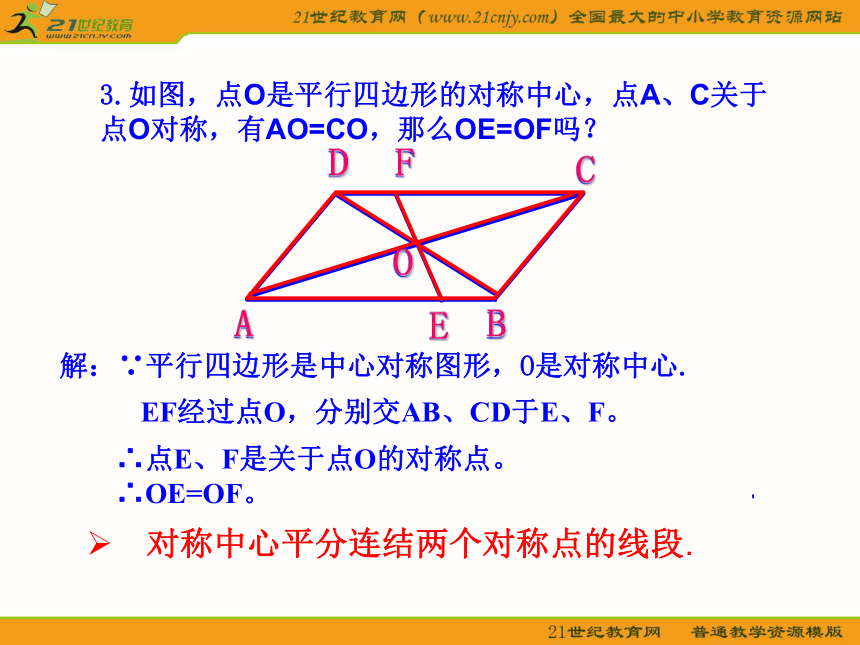
A’B’C’2. 如图,已知等边三角形ABC和点O,画△A’B’C’,使△A’B’C’和△ABC关于点O成中心对称。3.如图,点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,那么OE=OF吗? 对称中心平分连结两个对称点的线段.EF经过点O,分别交AB、CD于E、F。解:∵平行四边形是中心对称图形,O是对称中心.∴点E、F是关于点O的对称点。
∴OE=OF。4.正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转900旋转1800正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?是中心对称图形旋转2700正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转3600正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转nx900 正方形是中心对称图形;它绕两条对角线的交点旋转900或其整数倍,都能与原来的图形重合,因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?2.在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有__________________,是中心对称图形的有____________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨①②③④⑥⑦⑧⑨①⑥⑦⑧⑨B练习2 3. 判断下列说法是否正确(1)轴对称图形也是中心对称图形。( )(2)旋转对称图形也是中心对称图形。( )(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( )(4)角是轴对称图形也是中心对称图形。( )(5)在成中心对称的两个图形中,对应线段平行
(或在同一直线上)且相等。 ( )×√×√×4.若两个图形关于某一点成中心对称,那么下列说法:
对称点的连线必过对称中心;
这两个图形一定全等;
对应线段一定平行且相等;
将一个图形绕对称中心旋转180°必定与另一个图形重合。
其中正确的是( )。
(A) ①② (B) ①③ (C) ①②③ (D) ①②③④
5.如图,如果正方形CDEF旋转后能与正 方形ABCD重合,那么图形所在的平面 上可以作为旋转中心的点共有( )。
(A) 4 (B) 3 (C) 2 (D) 1CB1.正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。探索发现2.下面的扑克牌中,哪些牌面是中心对称图形?探索发现 3.在26个英文大写正体字母中,哪些字母是中心对称图形?A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z探索发现
A’B’C’2. 如图,已知等边三角形ABC和点O,画△A’B’C’,使△A’B’C’和△ABC关于点O成中心对称。3.如图,点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,那么OE=OF吗? 对称中心平分连结两个对称点的线段.EF经过点O,分别交AB、CD于E、F。解:∵平行四边形是中心对称图形,O是对称中心.∴点E、F是关于点O的对称点。
∴OE=OF。4.正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转900旋转1800正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?是中心对称图形旋转2700正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转3600正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转nx900 正方形是中心对称图形;它绕两条对角线的交点旋转900或其整数倍,都能与原来的图形重合,因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?2.在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有__________________,是中心对称图形的有____________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨①②③④⑥⑦⑧⑨①⑥⑦⑧⑨B练习2 3. 判断下列说法是否正确(1)轴对称图形也是中心对称图形。( )(2)旋转对称图形也是中心对称图形。( )(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( )(4)角是轴对称图形也是中心对称图形。( )(5)在成中心对称的两个图形中,对应线段平行
(或在同一直线上)且相等。 ( )×√×√×4.若两个图形关于某一点成中心对称,那么下列说法:
对称点的连线必过对称中心;
这两个图形一定全等;
对应线段一定平行且相等;
将一个图形绕对称中心旋转180°必定与另一个图形重合。
其中正确的是( )。
(A) ①② (B) ①③ (C) ①②③ (D) ①②③④
5.如图,如果正方形CDEF旋转后能与正 方形ABCD重合,那么图形所在的平面 上可以作为旋转中心的点共有( )。
(A) 4 (B) 3 (C) 2 (D) 1CB1.正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。探索发现2.下面的扑克牌中,哪些牌面是中心对称图形?探索发现 3.在26个英文大写正体字母中,哪些字母是中心对称图形?A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z探索发现
同课章节目录
