【期末押题预测】机械能守恒定律(含解析)2024-2025学年高中物理必修二教科版(2019)高一下册
文档属性
| 名称 | 【期末押题预测】机械能守恒定律(含解析)2024-2025学年高中物理必修二教科版(2019)高一下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1017.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-27 14:18:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末押题预测 机械能守恒定律
一.选择题(共5小题)
1.(2025 重庆一模)北京时间2024年11月4日01时24分,神舟十八号载人飞船返回舱在东风着陆场成功着陆。返回舱在打开降落伞后的一段匀速下落过程中,其机械能( )
A.不变 B.减少 C.增加 D.无法确定
2.(2025 福州校级模拟)2024年6月2日至3日,嫦娥六号顺利完成了在月球背面南极—艾特肯盆地的智能快速采样,6月4日7时38分,嫦娥六号上升器携带月球样品自月球背面发射起飞,随后成功进入预定环月轨道,完成世界首次月球背面采样和起飞。已知嫦娥六号质量为m,月球半径为R,以无穷远处为零势能点,嫦娥六号在距月球表面高度为h时的引力势能可表示为(其中G为引力常量,M为月球质量)。若忽略月球的自转,嫦娥六号自月球表面开始发射到进入距离月球表面高度为h的预定环月轨道,至少需要对嫦娥六号做的功为( )
A.
B.
C.
D.
3.(2025 未央区校级模拟)如图所示,一个光滑的固定斜面,倾角θ=30°。劲度系数为k的轻弹簧一端固定在斜面底端,另一端与质量为2m的物体A拴接,另有质量为4m的物体B靠在A上,并施加沿斜面向下的力F=3mg作用在物体B上,系统处于静止。现减小F,使A,B以的加速度一起匀加速向上运动,弹簧始终在弹性限度内,重力加速度为g。则从开始匀加速后到F=0的过程中( )
A.F随位移非均匀变化
B.物体A、B动能增加量为
C.时,物体A、B之间的弹力大小为
D.弹簧弹性势能减小
4.(2025 浙江)地球和哈雷彗星绕太阳运行的轨迹如图所示,彗星从a运行到b、从c运行到d的过程中,与太阳连线扫过的面积分别为S1和S1,且S1>S2。彗星在近日点与太阳中心的距离约为地球公转轨道半径的0.6倍,则彗星( )
A.在近日点的速度小于地球的速度
B.从b运行到c的过程中动能先增大后减小
C.从a运行到b的时间大于从c运行到d的时间
D.在近日点加速度约为地球的加速度的0.36倍
5.(2025 雨花区校级开学)如图所示,绕过定滑轮1、2的轻质细线一端吊着小球A,另一端连接可视为质点的物块B,物AC块B放在光滑水平面上,此时细线处于伸直状态。现将小球A由静止释放,至物块B沿水平岛面运动到定滑轮2正下方的过程中(不计滑轮的大小、质量和摩擦,物块B运动到滑轮2正下方时,小球A还未落地),下列说法正确的是( )
A.小球A和物块B的速率始终相等
B.小球A先超重后失重
C.小球A的合力先做正功后做负功
D.小球A的机械能先增大后减小
二.多选题(共4小题)
(多选)6.(2025 城关区校级开学)如图所示的传送带由水平部分和倾斜部分组成,倾斜部分与水平方向的夹角为37°。传送带以某一速度按图示方向运转,t=0时,将一质量为m=1kg的小滑块轻放在传送带的最顶端,以后滑块的速度大小与时间的变化关系如图所示,t=2.2s时滑块刚好到达最右端,物块在两传送带交接处运动时无机械能损失,重力加速度g=10m/s2,下列说法正确的是( )
A.滑块与传送带间的动摩擦因数为μ=0.6
B.滑块运动过程中能够达到的最大速度为vm=8m/s
C.传送带水平部分的总长度为l=3.6m
D.从t=0到t=0.6s的过程中,电动机额外提供电能E=14.4J
(多选)7.(2025 高新区校级模拟)如图所示,在竖直平面直角坐标系xOy中,在t=0时,质量m=0.5kg的小球从坐标原点O处,以初速度斜向右上方抛出,同时受到F风=5N的作用(虚线箭头为风力方向与v0的夹角为30°,且与x轴正方向的夹角也为30°),重力加速度g取10m/s2。下列说法正确的是( )
A.小球的加速度先增大后减小
B.小球在t=0.6s时再次经过x轴
C.小球的重力势能一直减小
D.小球的动能一直增大
(多选)8.(2025 兰州校级一模)如图甲所示,斜面倾角为α=30°、足够长、光滑的斜面体固定在水平地面上,可视为质点的质量为m=4kg的物块置于斜面上足够高处,t=0时刻在物块上施加一沿斜面向上的变化的外力,同时释放物块,利用计算机描绘了0~4s时间内物块的速度随时间的变化图象,如图乙所示,规定沿斜面向下的方向为正方向,物块在释放点的重力势能为零,重力加速度大小为g=10m/s2。则( )
A.1~2s的时间内外力的大小为40N
B.0~1s时间内与2~4s时间内的外力大小之比为2:19
C.1s末物块的机械能为32J
D.0~4s的时间内物块的机械能减少了350J
(多选)9.(2024秋 郴州期末)如图所示,一劲度系数为k=1N/cm的轻质弹簧左端固定在竖直墙壁上,弹簧右端固定有一质量为m=2kg的物块,物块与水平地面间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力。用力向左推动物块使弹簧压缩量达到x1=11cm后由静止释放物块,重力加速度g=10m/s2,不计空气阻力,下列说法正确的是( )
A.释放后瞬间物块的加速度大小为5m/s2
B.物块第一次向右运动的最大距离为18cm
C.物块最终停在弹簧的原长左侧1cm处
D.物块从静止释放,到最终停下,整个过程中因摩擦而产生的内能为0.56J
三.填空题(共3小题)
10.(2024秋 思明区校级月考)如图,轻质弹簧一端固定在墙壁上,另一端与质量m=0.1kg的滑块相连,滑块放置在光滑水平面上。将滑块从弹簧原长位置O向左移至B处并由静止释放,滑块在B、C间往复运动,设弹簧被压缩到B处时具有的弹性势能为5J,则滑块从B运动到O的过程中速度 (选填“A.变大”“B.变小”“C.不变”);滑块运动的最大速度为 m/s,滑块从O到C的过程中滑块与弹簧组成的系统总能量 (选填“A.变大”“B.变小”“C.不变”)。
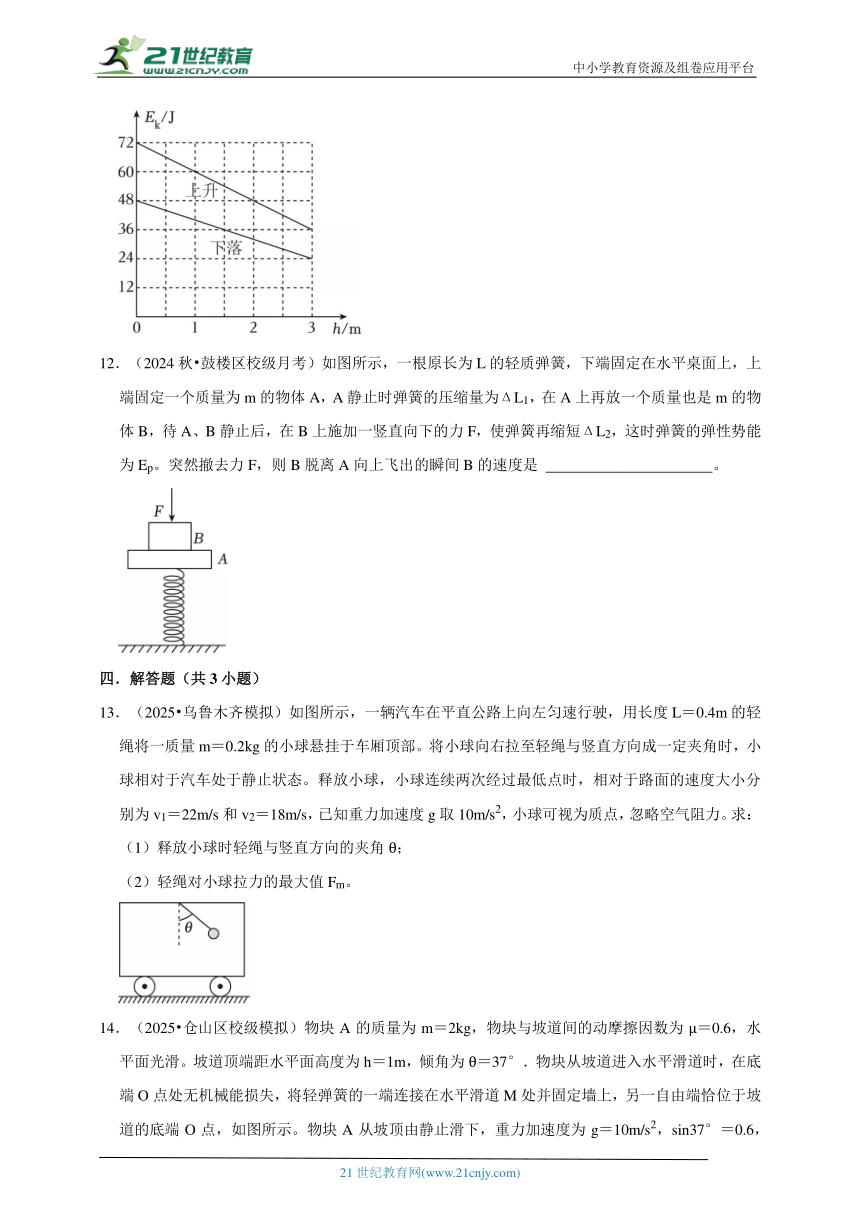
11.(2024 福建模拟)从地面竖直向上抛出一物体,物体在运动过程中除受到重力外,还受到阻力作用。物体上升、下落过程中动能Ek随高度h的变化的部分图像如图所示。重力加速度取10m/s2。则该物体所受阻力是恒力,大小为 N,该物体的质量为 kg,整个过程损失的机械能是 J。
12.(2024秋 鼓楼区校级月考)如图所示,一根原长为L的轻质弹簧,下端固定在水平桌面上,上端固定一个质量为m的物体A,A静止时弹簧的压缩量为ΔL1,在A上再放一个质量也是m的物体B,待A、B静止后,在B上施加一竖直向下的力F,使弹簧再缩短ΔL2,这时弹簧的弹性势能为Ep。突然撤去力F,则B脱离A向上飞出的瞬间B的速度是 。
四.解答题(共3小题)
13.(2025 乌鲁木齐模拟)如图所示,一辆汽车在平直公路上向左匀速行驶,用长度L=0.4m的轻绳将一质量m=0.2kg的小球悬挂于车厢顶部。将小球向右拉至轻绳与竖直方向成一定夹角时,小球相对于汽车处于静止状态。释放小球,小球连续两次经过最低点时,相对于路面的速度大小分别为v1=22m/s和v2=18m/s,已知重力加速度g取10m/s2,小球可视为质点,忽略空气阻力。求:
(1)释放小球时轻绳与竖直方向的夹角θ;
(2)轻绳对小球拉力的最大值Fm。
14.(2025 仓山区校级模拟)物块A的质量为m=2kg,物块与坡道间的动摩擦因数为μ=0.6,水平面光滑。坡道顶端距水平面高度为h=1m,倾角为θ=37°.物块从坡道进入水平滑道时,在底端O点处无机械能损失,将轻弹簧的一端连接在水平滑道M处并固定墙上,另一自由端恰位于坡道的底端O点,如图所示。物块A从坡顶由静止滑下,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量时的弹性势能;
(3)物块A被弹回到坡道后上升的最大高度。
15.(2024秋 房山区期末)如图所示,光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接,导轨半径为0.40m。一个质量为0.20kg的物体将弹簧压缩至A点后由静止释放,在弹簧弹力作用下,物体脱离弹簧向右运动。经B点沿半圆形导轨运动,到达C点后水平飞出,恰好落在A点。已知B点的速度大小为5.0m/s,A、B两点距离为0.80m,取重力加速度g为10m/s2。求:
(1)物体到达C点的速度大小v。
(2)物体沿半圆形导轨运动过程中阻力所做的功W。
(3)弹簧压缩至A点时的弹性势能Ep。
期末押题预测 机械能守恒定律
参考答案与试题解析
题号 1 2 3 4 5
答案 B B D C C
一.选择题(共5小题)
1.(2025 重庆一模)北京时间2024年11月4日01时24分,神舟十八号载人飞船返回舱在东风着陆场成功着陆。返回舱在打开降落伞后的一段匀速下落过程中,其机械能( )
A.不变 B.减少 C.增加 D.无法确定
【考点】判断机械能是否守恒及如何变化.
【专题】定性思想;推理法;机械能守恒定律应用专题;推理论证能力.
【答案】B
【分析】结合题意,先判断返回舱的动能及重力势能如何变化,即可判断其机械能如何变化,即可分析判断ABCD正误。
【解答】解:因为返回舱在打开降落伞后匀速下落,所以其动能不变,因为返回舱在下落,所以其重力势能减小,因为返回舱的机械能等于其动能与重力势能的和,所以返回舱在打开降落伞后的一段匀速下落过程中,其机械能减少,故B正确,ACD错误;
故选:B。
【点评】本题考查了判断机械能是否守恒及如何变化,解题时需注意,如果除重力或系统内弹力外还有其他力做正功,则系统的机械能增大;如果除重力或系统内弹力外还有其他力做负功,则系统的机械能减小;此类题也可以通过先判断动能与势能如何变化,进而判断机械能如何变化。
2.(2025 福州校级模拟)2024年6月2日至3日,嫦娥六号顺利完成了在月球背面南极—艾特肯盆地的智能快速采样,6月4日7时38分,嫦娥六号上升器携带月球样品自月球背面发射起飞,随后成功进入预定环月轨道,完成世界首次月球背面采样和起飞。已知嫦娥六号质量为m,月球半径为R,以无穷远处为零势能点,嫦娥六号在距月球表面高度为h时的引力势能可表示为(其中G为引力常量,M为月球质量)。若忽略月球的自转,嫦娥六号自月球表面开始发射到进入距离月球表面高度为h的预定环月轨道,至少需要对嫦娥六号做的功为( )
A.
B.
C.
D.
【考点】天体运动中机械能的变化.
【专题】定量思想;推理法;万有引力定律的应用专题;推理论证能力.
【答案】B
【分析】嫦娥六号绕月球做匀速圆周运动,万有引力提供向心力,应用牛顿第二定律求出嫦娥六号的速度,然后应用功能关系求出发生嫦娥六号需要做的功。
【解答】解:根据万有引力提供向心力,得
根据动能表达式,嫦娥六号在环月轨道绕月球做圆周运动的动能
联立以上两式解得
嫦娥六号在h0高度的引力势能为
Ep
在月球表面的引力势能为
根据功能关系,从开始发射到进入预定环月轨道需要对嫦娥六号做的功为
,故ACD错误,B正确。
故选:B。
【点评】本题考查了万有引力定律的应用,根据题意应用牛顿第二定律、功能关系即可解题。
3.(2025 未央区校级模拟)如图所示,一个光滑的固定斜面,倾角θ=30°。劲度系数为k的轻弹簧一端固定在斜面底端,另一端与质量为2m的物体A拴接,另有质量为4m的物体B靠在A上,并施加沿斜面向下的力F=3mg作用在物体B上,系统处于静止。现减小F,使A,B以的加速度一起匀加速向上运动,弹簧始终在弹性限度内,重力加速度为g。则从开始匀加速后到F=0的过程中( )
A.F随位移非均匀变化
B.物体A、B动能增加量为
C.时,物体A、B之间的弹力大小为
D.弹簧弹性势能减小
【考点】常见力做功与相应的能量转化;胡克定律及其应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】D
【分析】根据牛顿第二定律得到F与位移的关系,根据动能定理求解物体A、B动能增加量,对B进行分析得到物体A、B之间的弹力大小,弹性势能变化量的值等于弹簧弹力做功。
【解答】解:A.由题意得,最初A、B静止,根据受力平衡,弹簧弹力大小为
F0=6mgsinθ+3mg=6mg=kx0
当A、B开始匀加速运动,运动位移为x时有
k(x0﹣x)﹣6mgsinθ﹣F=6ma
可得
F=2mg﹣kx
由表达式可知F随位移均匀变化,故A错误;
B.当F = 0时,结合上述有
根据动能定理有
6max=Ek﹣0
结合上述解得
故B错误;
C.对B进行分析,当,有
NAB﹣4mgsinθ﹣F=4ma
结合上述解得
NAB=3mg
故C错误;
D.弹性势能变化量的值等于弹簧弹力做功
故D正确。
故选:D。
【点评】解答本题时,要灵活选择研究对象,采用隔离法和整体法相结合处理,比较简洁。要注意分析弹簧的状态,确定弹力的方向。
4.(2025 浙江)地球和哈雷彗星绕太阳运行的轨迹如图所示,彗星从a运行到b、从c运行到d的过程中,与太阳连线扫过的面积分别为S1和S1,且S1>S2。彗星在近日点与太阳中心的距离约为地球公转轨道半径的0.6倍,则彗星( )
A.在近日点的速度小于地球的速度
B.从b运行到c的过程中动能先增大后减小
C.从a运行到b的时间大于从c运行到d的时间
D.在近日点加速度约为地球的加速度的0.36倍
【考点】天体运动中机械能的变化;开普勒三大定律.
【专题】定量思想;推理法;万有引力定律在天体运动中的应用专题;推理论证能力.
【答案】C
【分析】根据高轨低速大周期的二级结论分析;根据万有引力做功情况分析;根据开普勒第二定律分析;根据牛顿第二定律分析。
【解答】解:A、假设彗星以0.6r绕太阳做匀速圆周运动为轨道1速度为v1,地球绕太阳做圆周运动为轨道3环绕速度为v3,根据高轨低速的推论,可知v1>3,如果彗星从轨道1变为原本的椭圆轨道(设为轨道2),要做离心运动,需要在近地点瞬间加速,则彗星在原本椭圆轨道近日点的速度,v2>v1,综上所述,v2>v3,即彗星在近日点的速度大于地球的速度,故A错误;
B、彗星从b运行到c的过程中,万有引力一直做负功,动能一直减小,故B错误;
C、根据开普勒第二定律,可知彗星从a运行到b的时间大于从c到a的运行时间,故C正确;
D、对于地球绕太阳的匀速圆周运动,设环绕半径为r,根据牛顿第二定律,解得;对于彗星在近日点,根据牛顿第二第二定律有,解得a,故D错误。
故选:C。
【点评】本题考查了万有引力定律和开普勒定律在天体运动中的应用问题,记住二级结论高轨低速大周期可以快速判断。
5.(2025 雨花区校级开学)如图所示,绕过定滑轮1、2的轻质细线一端吊着小球A,另一端连接可视为质点的物块B,物AC块B放在光滑水平面上,此时细线处于伸直状态。现将小球A由静止释放,至物块B沿水平岛面运动到定滑轮2正下方的过程中(不计滑轮的大小、质量和摩擦,物块B运动到滑轮2正下方时,小球A还未落地),下列说法正确的是( )
A.小球A和物块B的速率始终相等
B.小球A先超重后失重
C.小球A的合力先做正功后做负功
D.小球A的机械能先增大后减小
【考点】机械能守恒定律的简单应用;关联速度问题;功的正负及判断.
【专题】比较思想;合成分解法;机械能守恒定律应用专题;理解能力.
【答案】C
【分析】根据物块B沿细线方向的分速度大小与小球A的速度大小相等,分析小球A和物块B的速率是否相等;根据开始时与B运动到滑轮2的正下方时小球A的速度分析A的运动情况,再判断其运动状态;根据动能定理分析小球A的合力做功情况;根据细线拉力对小球A做功情况,分析小球A的机械能变化情况。
【解答】解:A、物块B沿细线方向的分速度大小与小球A的速度大小始终相等,故A错误;
B、开始时,小球A的速度为零。当物块B运动到滑轮2的正下方时,小球A的速度也为零,所以小球A向下先加速后减速到速度为零,加速度先向下后向上,先失重后超重,故B错误;
C、小球A的动能先增大后减小,根据动能定理可知,小球A的合力先做正功后做负功,故C正确;
D、细线对小球A的拉力一直做负功,所以小球A的机械能一直减少,故D错误。
故选:C。
【点评】本题是牵连速度问题,要知道物块B沿细线方向的分速度大小与小球A的速度大小始终相等,当当物块B运动到滑轮2的正下方时,小球A的速度为零,来分析A的运动情况,判断合力做功情况。
二.多选题(共4小题)
(多选)6.(2025 城关区校级开学)如图所示的传送带由水平部分和倾斜部分组成,倾斜部分与水平方向的夹角为37°。传送带以某一速度按图示方向运转,t=0时,将一质量为m=1kg的小滑块轻放在传送带的最顶端,以后滑块的速度大小与时间的变化关系如图所示,t=2.2s时滑块刚好到达最右端,物块在两传送带交接处运动时无机械能损失,重力加速度g=10m/s2,下列说法正确的是( )
A.滑块与传送带间的动摩擦因数为μ=0.6
B.滑块运动过程中能够达到的最大速度为vm=8m/s
C.传送带水平部分的总长度为l=3.6m
D.从t=0到t=0.6s的过程中,电动机额外提供电能E=14.4J
【考点】常见力做功与相应的能量转化;复杂的运动学图像问题;牛顿第二定律的简单应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】BD
【分析】A.从t=0到t=0.6s的过程中,结合题图及牛顿第二定律分别列式,即可分析判断;
B.从t=0.6s到t=1.6s过程中,结合题图,根据牛顿第二定律、匀变速直线运动规律分别列式,即可分析判断;
C.结合前面分析,由运动学规律分别列式,即可分析判断;
D.结合前面分析,从t=0到t=0.6s的过程中,根据功能关系及运动学规律分别列式,即可分析判断。
【解答】解:A.由图可知,从t=0到t=0.6s的过程中,物块在倾斜传送带上做加速运动,当t=0.6s时物块与传送带共速,均为6m/s,
则该过程加速度大小为:,
根据牛顿第二定律可得:mgsin37°+μmgcos37°=ma1,
联立可得:μ=0.5,
故A错误;
B.由图可知,t=0.6s到t=1.6s过程中,物块在倾斜传送带上继续加速,但由于物块速度大于传送带速度,
根据牛顿第二定律可得:mgsin37°﹣μmgcos37°=ma2,
再结合匀变速直线运动规律可得:vm﹣v1=a2t2,
其中:v1=6m/s,t2=1.6s﹣0.6s=1s,
联立可得:vm=8m/s,
故B正确;
C.结合前面分析可知,当滑块在水平传送带上减速时,
有:vm﹣v1=μgΔt,
解得:Δt=0.4s,
传送带水平部分长度为:lv1(0.6s﹣Δt),
联立可得:l=4m,
故C错误;
D.结合前面分析可知,从t=0到t=0.6s的过程中,根据功能关系可知,
电动机额外提供电能为:E=μmgcosθ x1,
其中:x1=v1t=6×0.6m=3.6m,
联立可得:E=14.4J,
故D正确;
故选:BD。
【点评】本题主要考查对牛顿第二定律的掌握,解题时需注意,应用牛顿第二定律解决简单问题时,要先明确物体的受力情况,然后列出牛顿第二定律的表达式,再根据需要求出相关物理量。
(多选)7.(2025 高新区校级模拟)如图所示,在竖直平面直角坐标系xOy中,在t=0时,质量m=0.5kg的小球从坐标原点O处,以初速度斜向右上方抛出,同时受到F风=5N的作用(虚线箭头为风力方向与v0的夹角为30°,且与x轴正方向的夹角也为30°),重力加速度g取10m/s2。下列说法正确的是( )
A.小球的加速度先增大后减小
B.小球在t=0.6s时再次经过x轴
C.小球的重力势能一直减小
D.小球的动能一直增大
【考点】常见力做功与相应的能量转化;斜抛运动.
【专题】定量思想;推理法;平抛运动专题;推理论证能力.
【答案】BD
【分析】由题意和几何知识可知小球受到的合力与初速度的方向垂直,小球做类平抛运动,结合牛顿第二定律以及运动学公式分析。
【解答】解:A.由题意和几何知识可知小球受到的合力为
F=5N
方向与初速度的方向垂直,小球做类平抛运动,小球的加速度不变,故A错误;
B.小球再次经过x轴时,沿初速度方向的位移和垂直初速度的位移关系为
又
解得
t=0.6s
故B正确;
C.小球做类平抛运动,小球的高度先增加后减小,重力势能先增加后减小,故C错误;
D.小球做类平抛运动,速度一直在增加,小球的动能一直增大,故D正确。
故选:BD。
【点评】本题解题关键是分析出小球受到的合力与初速度的方向垂直,小球做类平抛运动。
(多选)8.(2025 兰州校级一模)如图甲所示,斜面倾角为α=30°、足够长、光滑的斜面体固定在水平地面上,可视为质点的质量为m=4kg的物块置于斜面上足够高处,t=0时刻在物块上施加一沿斜面向上的变化的外力,同时释放物块,利用计算机描绘了0~4s时间内物块的速度随时间的变化图象,如图乙所示,规定沿斜面向下的方向为正方向,物块在释放点的重力势能为零,重力加速度大小为g=10m/s2。则( )
A.1~2s的时间内外力的大小为40N
B.0~1s时间内与2~4s时间内的外力大小之比为2:19
C.1s末物块的机械能为32J
D.0~4s的时间内物块的机械能减少了350J
【考点】常见力做功与相应的能量转化;牛顿第二定律的简单应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】BD
【分析】v﹣t图像斜率表示加速度,v﹣t图像面积表示位移,结合牛顿第二定律求解拉力F大小,物块机械能的变化量等于整个过程外力F所做的功,外力F所做的功等于力与位移乘积。
【解答】解:A.由图乙可知,1s~2s时内物块的加速度为
位移大小为
由牛顿第二定律得
mgsin30°﹣F2=ma2
解得
F2=0
故A错误;
B.由图乙可知,0 1s时内物块的加速度为
位移大小为
由牛顿第二定律得
mgsin30°﹣F1=ma1
解得
F1=4N
由图乙可知,2s~4s时内物块的加速度为
位移大小为
由牛顿第二定律得
mgsin30°﹣F3=ma3
解得
F3=38N
则
F1:F3=2:19
故B正确;
CD.由题意可知,t=0时刻,物块的机械能为0,由功能关系可知,物块机械能的变化量等于整个过程外力F所做的功,0 1s外力做的功为
W1=F1x1=﹣4×2J=﹣8J
即1s末物块的机械能为﹣8J,2s~4s外力做的功为
W3=F3x3=﹣38×9J=﹣342J
则整个过程中物块机械能变化量大小为
ΔE=|W1+W3|=350J
故C错误,D正确。
故选:BD。
【点评】解题关键是知道v﹣t图像的面积等于位移,v﹣t图像的斜率表示加速度。
(多选)9.(2024秋 郴州期末)如图所示,一劲度系数为k=1N/cm的轻质弹簧左端固定在竖直墙壁上,弹簧右端固定有一质量为m=2kg的物块,物块与水平地面间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力。用力向左推动物块使弹簧压缩量达到x1=11cm后由静止释放物块,重力加速度g=10m/s2,不计空气阻力,下列说法正确的是( )
A.释放后瞬间物块的加速度大小为5m/s2
B.物块第一次向右运动的最大距离为18cm
C.物块最终停在弹簧的原长左侧1cm处
D.物块从静止释放,到最终停下,整个过程中因摩擦而产生的内能为0.56J
【考点】常见力做功与相应的能量转化;牛顿第二定律的简单应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】BC
【分析】由牛顿第二定律求解加速度,向右运动的最大位移和释放点关于该平衡位置对称,物块向左运动的过程中,求解新的平衡位置,摩擦产生的热量等于摩擦力乘以相对位移。
【解答】解:质量为m=2kg的物块,物块与水平地面间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力,劲度系数为k=1N/cm的轻质弹簧
由牛顿第二定律
kx1﹣μmg=ma
得加速度
a=4.5m/s2
平衡位置为
kx2=μmg
x2=2cm
向右运动的最大位移和释放点关于该平衡位置对称,所以物块第一次向右运动的最大距离为18cm;物块向左运动的过程中,在新的平衡位置
kx3=μmg
x3=x2=2cm
所以物块向左运动10cm,以此类推,物块第二次向右运动2cm后停下来,所以物块停在距离弹簧原长左侧1cm处,总路程为30cm,从而摩擦产生的热量为
Q=μmgs=0.1×20×0.3J=0.6J,故AD错误,BC正确。
故选:BC。
【点评】物体向一个方向运动时,摩擦力恒定,可以看成在摩擦力和弹力共同作用下的简谐运动。
三.填空题(共3小题)
10.(2024秋 思明区校级月考)如图,轻质弹簧一端固定在墙壁上,另一端与质量m=0.1kg的滑块相连,滑块放置在光滑水平面上。将滑块从弹簧原长位置O向左移至B处并由静止释放,滑块在B、C间往复运动,设弹簧被压缩到B处时具有的弹性势能为5J,则滑块从B运动到O的过程中速度 变大 (选填“A.变大”“B.变小”“C.不变”);滑块运动的最大速度为 10 m/s,滑块从O到C的过程中滑块与弹簧组成的系统总能量 不变 (选填“A.变大”“B.变小”“C.不变”)。
【考点】弹簧类问题中的机械能守恒.
【专题】定量思想;推理法;机械能守恒定律应用专题;推理论证能力.
【答案】变大;10;不变
【分析】根据机械能守恒定律分析能量变化,从而分析最大速度的位置,根据机械能守恒定律列式计算最大速度。
【解答】解:滑块从B运动到O的过程中,弹簧弹性势能减小,动能增大,则速度变大,则O点的速度最大,根据机械能守恒定律有
Ep
解得v=10m/s
根据机械能守恒定律可知,滑块从O到C的过程中滑块与弹簧组成的系统总能量不变。
故答案为:变大;10;不变
【点评】本题关键是明确机械能守恒定律答应用,解题关键掌握能量的转化特点。
11.(2024 福建模拟)从地面竖直向上抛出一物体,物体在运动过程中除受到重力外,还受到阻力作用。物体上升、下落过程中动能Ek随高度h的变化的部分图像如图所示。重力加速度取10m/s2。则该物体所受阻力是恒力,大小为 2 N,该物体的质量为 1 kg,整个过程损失的机械能是 24 J。
【考点】机械能与图像相结合的问题.
【专题】定量思想;推理法;机械能守恒定律应用专题;分析综合能力.
【答案】2;1;24。
【分析】Ek﹣h图象的斜率大小等于物体受到的合力,根据斜率可以求出物体的质量和所受阻力;根据动能定理可求物体上升的最大高度,整个过程应用功能关系求出机械能的损失。
【解答】解:Ek﹣h图象的斜率大小等于物体受到的合力,上升过程和下降过程的斜率不变,说明阻力是恒力,设空气阻力为F,则上升过程有:
下落过程有
联立解得
m=1kg,F=2N,
设物体上升的最大高度为H,由动能定理得
(mg+F)H=Ek0
解得
H=6m,
整个过程损失的机械能等于克服阻力做的功
ΔE=F×2H
解得
ΔE=24J
故答案为:2;1;24。
【点评】解决该题的关键是明确图象中斜率的大小表示的是物体受到的合外力,知道上升和下降过程中合外力的表达式。知道机械能的变化等于除重力外其它力做的功。
12.(2024秋 鼓楼区校级月考)如图所示,一根原长为L的轻质弹簧,下端固定在水平桌面上,上端固定一个质量为m的物体A,A静止时弹簧的压缩量为ΔL1,在A上再放一个质量也是m的物体B,待A、B静止后,在B上施加一竖直向下的力F,使弹簧再缩短ΔL2,这时弹簧的弹性势能为Ep。突然撤去力F,则B脱离A向上飞出的瞬间B的速度是 。
【考点】弹簧类问题中的机械能守恒.
【专题】定量思想;方程法;机械能守恒定律应用专题;推理论证能力.
【答案】。
【分析】分离瞬间加速度相同,相互作用力为零,整个运动过程中系统机械能守恒,根据机械能守恒定律即可求解。
【解答】解:分离瞬间加速度相同,相互作用力为零,从撤除力到A、B分离,系统机械能守恒,则有:Ep=2mg(2ΔL1+ΔL2) 2mv2
解得:v。
故答案为:。
【点评】本题主要考查了械能守恒定律的应用,知道在分离的瞬间,AB加速度相同,之间的作用力为零。
四.解答题(共3小题)
13.(2025 乌鲁木齐模拟)如图所示,一辆汽车在平直公路上向左匀速行驶,用长度L=0.4m的轻绳将一质量m=0.2kg的小球悬挂于车厢顶部。将小球向右拉至轻绳与竖直方向成一定夹角时,小球相对于汽车处于静止状态。释放小球,小球连续两次经过最低点时,相对于路面的速度大小分别为v1=22m/s和v2=18m/s,已知重力加速度g取10m/s2,小球可视为质点,忽略空气阻力。求:
(1)释放小球时轻绳与竖直方向的夹角θ;
(2)轻绳对小球拉力的最大值Fm。
【考点】机械能守恒定律的简单应用;牛顿第二定律的简单应用;牛顿第二定律与向心力结合解决问题.
【专题】计算题;定量思想;寻找守恒量法;机械能守恒定律应用专题;分析综合能力.
【答案】(1)释放小球时轻绳与竖直方向的夹角θ为60°;
(2)轻绳对小球拉力的最大值Fm为4N。
【分析】(1)设车的速度大小为v车,小球运动过程中相对于车的最大速度为vm,当小球向左经过最低点时,有v1=v车+vm;当小球向右经过最低点时,有v2=v车﹣vm,由此求出vm。再以车厢为参考系,根据机械能守恒定律求释放小球时轻绳与竖直方向的夹角θ;
(2)小球经过最低点时,根据牛顿第二定律求解轻绳对小球拉力的最大值Fm。
【解答】解:(1)取向左为正方向,设车的速度大小为v车,小球运动过程中相对于车的最大速度为vm。
小球向左经过最低点时的速度v1=v车+vm
小球向右经过最低点时的速度v2=v车﹣vm
解得
vm=2m/s
以车厢为参考系,小球由释放至运动到最低点的过程中,根据机械能守恒定律有
mgL(1﹣cosθ)
解得θ=60°
(2)小球经过最低点时,根据牛顿第二定律有
Fm﹣mg=m
解得Fm=4N
答:(1)释放小球时轻绳与竖直方向的夹角θ为60°;
(2)轻绳对小球拉力的最大值Fm为4N。
【点评】解答本题时,要理解运动的相对性,要知道匀速运动的参考系与静止参考系遵守相同的物理规律。
14.(2025 仓山区校级模拟)物块A的质量为m=2kg,物块与坡道间的动摩擦因数为μ=0.6,水平面光滑。坡道顶端距水平面高度为h=1m,倾角为θ=37°.物块从坡道进入水平滑道时,在底端O点处无机械能损失,将轻弹簧的一端连接在水平滑道M处并固定墙上,另一自由端恰位于坡道的底端O点,如图所示。物块A从坡顶由静止滑下,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量时的弹性势能;
(3)物块A被弹回到坡道后上升的最大高度。
【考点】弹簧类问题中的机械能守恒;动能定理的简单应用.
【专题】计算题;定性思想;推理法;动能定理的应用专题;机械能守恒定律应用专题;理解能力.
【答案】见试题解答内容
【分析】(1)物块A从坡顶滑下,重力和摩擦力做功,根据动能定理可求出物块滑到O点时的速度大小。
(2)物块压缩弹簧后,物块和弹簧组成的系统机械能守恒,根据机械能守恒定律可弹性势能。
(3)物块滑回到O点时与刚滑到O点时速度大小相等,从坡底到坡顶,再动能定理求解最大高度。
【解答】解:(1)由动能定理得:
解得:,
代入数据得:v=2m/s
(2)在水平滑道上,由机械能守恒定律得:mv2=Ep
代入数据得:Ep=4J
(3)设物块A能够上升的最大高度为h1,物块被弹回过程中由动能定理得:
代入数据解得:h1m
答:(1)物块滑到O点时的速度大小是2m/s。
(2)弹簧为最大压缩量时的弹性势能为4J。
(3)物块A被弹回到坡道后上升的最大高度是m。
【点评】本题是动能定理与机械能守恒定律的简单运用。对动能定理的运用,要选择研究过程,分析哪些力对物体做功,进而确定合力的功或总功。
15.(2024秋 房山区期末)如图所示,光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接,导轨半径为0.40m。一个质量为0.20kg的物体将弹簧压缩至A点后由静止释放,在弹簧弹力作用下,物体脱离弹簧向右运动。经B点沿半圆形导轨运动,到达C点后水平飞出,恰好落在A点。已知B点的速度大小为5.0m/s,A、B两点距离为0.80m,取重力加速度g为10m/s2。求:
(1)物体到达C点的速度大小v。
(2)物体沿半圆形导轨运动过程中阻力所做的功W。
(3)弹簧压缩至A点时的弹性势能Ep。
【考点】多物体系统的机械能守恒问题;平抛运动速度的计算;动能定理的简单应用;弹簧类问题中的机械能守恒.
【专题】定量思想;推理法;平抛运动专题;动能定理的应用专题;机械能守恒定律应用专题;推理论证能力.
【答案】(1)物体到达C点的速度大小v为2m/s;
(2)物体沿半圆形导轨运动过程中阻力所做的功W为﹣0.5J;
(3)弹簧压缩至A点时的弹性势能Ep为2.5J。
【分析】(1)物体由C到A做平抛运动,由平抛运动的运动规律分别列式,即可分析求解;
(2)物体沿半圆形导轨运动过程中,由动能定理列式,即可分析求解;
(3)释放物体的过程,由机械能守恒定律列式,即可分析求解。
【解答】解:(1)物体由C到A做平抛运动,由平抛运动的运动规律可知,
水平方向有:xBA=vt,
竖直方向有:2Rgt2,
由题知:xBA=0.80m,R=0.40m,
联立可得:v=2m/s;
(2)物体沿半圆形导轨运动过程中,
由动能定理可得:﹣mg 2R+W,
由题知:m=0.20kg,vB=5.0m/s,
解得:W=﹣0.5J;
(3)释放物体的过程,弹簧与物体组成的系统机械能守恒,可得:Ep,
解得:Ep=2.5J;
答:(1)物体到达C点的速度大小v为2m/s;
(2)物体沿半圆形导轨运动过程中阻力所做的功W为﹣0.5J;
(3)弹簧压缩至A点时的弹性势能Ep为2.5J。
【点评】本题主要考查多物体系统的机械能守恒问题,解题时需注意,在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末押题预测 机械能守恒定律
一.选择题(共5小题)
1.(2025 重庆一模)北京时间2024年11月4日01时24分,神舟十八号载人飞船返回舱在东风着陆场成功着陆。返回舱在打开降落伞后的一段匀速下落过程中,其机械能( )
A.不变 B.减少 C.增加 D.无法确定
2.(2025 福州校级模拟)2024年6月2日至3日,嫦娥六号顺利完成了在月球背面南极—艾特肯盆地的智能快速采样,6月4日7时38分,嫦娥六号上升器携带月球样品自月球背面发射起飞,随后成功进入预定环月轨道,完成世界首次月球背面采样和起飞。已知嫦娥六号质量为m,月球半径为R,以无穷远处为零势能点,嫦娥六号在距月球表面高度为h时的引力势能可表示为(其中G为引力常量,M为月球质量)。若忽略月球的自转,嫦娥六号自月球表面开始发射到进入距离月球表面高度为h的预定环月轨道,至少需要对嫦娥六号做的功为( )
A.
B.
C.
D.
3.(2025 未央区校级模拟)如图所示,一个光滑的固定斜面,倾角θ=30°。劲度系数为k的轻弹簧一端固定在斜面底端,另一端与质量为2m的物体A拴接,另有质量为4m的物体B靠在A上,并施加沿斜面向下的力F=3mg作用在物体B上,系统处于静止。现减小F,使A,B以的加速度一起匀加速向上运动,弹簧始终在弹性限度内,重力加速度为g。则从开始匀加速后到F=0的过程中( )
A.F随位移非均匀变化
B.物体A、B动能增加量为
C.时,物体A、B之间的弹力大小为
D.弹簧弹性势能减小
4.(2025 浙江)地球和哈雷彗星绕太阳运行的轨迹如图所示,彗星从a运行到b、从c运行到d的过程中,与太阳连线扫过的面积分别为S1和S1,且S1>S2。彗星在近日点与太阳中心的距离约为地球公转轨道半径的0.6倍,则彗星( )
A.在近日点的速度小于地球的速度
B.从b运行到c的过程中动能先增大后减小
C.从a运行到b的时间大于从c运行到d的时间
D.在近日点加速度约为地球的加速度的0.36倍
5.(2025 雨花区校级开学)如图所示,绕过定滑轮1、2的轻质细线一端吊着小球A,另一端连接可视为质点的物块B,物AC块B放在光滑水平面上,此时细线处于伸直状态。现将小球A由静止释放,至物块B沿水平岛面运动到定滑轮2正下方的过程中(不计滑轮的大小、质量和摩擦,物块B运动到滑轮2正下方时,小球A还未落地),下列说法正确的是( )
A.小球A和物块B的速率始终相等
B.小球A先超重后失重
C.小球A的合力先做正功后做负功
D.小球A的机械能先增大后减小
二.多选题(共4小题)
(多选)6.(2025 城关区校级开学)如图所示的传送带由水平部分和倾斜部分组成,倾斜部分与水平方向的夹角为37°。传送带以某一速度按图示方向运转,t=0时,将一质量为m=1kg的小滑块轻放在传送带的最顶端,以后滑块的速度大小与时间的变化关系如图所示,t=2.2s时滑块刚好到达最右端,物块在两传送带交接处运动时无机械能损失,重力加速度g=10m/s2,下列说法正确的是( )
A.滑块与传送带间的动摩擦因数为μ=0.6
B.滑块运动过程中能够达到的最大速度为vm=8m/s
C.传送带水平部分的总长度为l=3.6m
D.从t=0到t=0.6s的过程中,电动机额外提供电能E=14.4J
(多选)7.(2025 高新区校级模拟)如图所示,在竖直平面直角坐标系xOy中,在t=0时,质量m=0.5kg的小球从坐标原点O处,以初速度斜向右上方抛出,同时受到F风=5N的作用(虚线箭头为风力方向与v0的夹角为30°,且与x轴正方向的夹角也为30°),重力加速度g取10m/s2。下列说法正确的是( )
A.小球的加速度先增大后减小
B.小球在t=0.6s时再次经过x轴
C.小球的重力势能一直减小
D.小球的动能一直增大
(多选)8.(2025 兰州校级一模)如图甲所示,斜面倾角为α=30°、足够长、光滑的斜面体固定在水平地面上,可视为质点的质量为m=4kg的物块置于斜面上足够高处,t=0时刻在物块上施加一沿斜面向上的变化的外力,同时释放物块,利用计算机描绘了0~4s时间内物块的速度随时间的变化图象,如图乙所示,规定沿斜面向下的方向为正方向,物块在释放点的重力势能为零,重力加速度大小为g=10m/s2。则( )
A.1~2s的时间内外力的大小为40N
B.0~1s时间内与2~4s时间内的外力大小之比为2:19
C.1s末物块的机械能为32J
D.0~4s的时间内物块的机械能减少了350J
(多选)9.(2024秋 郴州期末)如图所示,一劲度系数为k=1N/cm的轻质弹簧左端固定在竖直墙壁上,弹簧右端固定有一质量为m=2kg的物块,物块与水平地面间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力。用力向左推动物块使弹簧压缩量达到x1=11cm后由静止释放物块,重力加速度g=10m/s2,不计空气阻力,下列说法正确的是( )
A.释放后瞬间物块的加速度大小为5m/s2
B.物块第一次向右运动的最大距离为18cm
C.物块最终停在弹簧的原长左侧1cm处
D.物块从静止释放,到最终停下,整个过程中因摩擦而产生的内能为0.56J
三.填空题(共3小题)
10.(2024秋 思明区校级月考)如图,轻质弹簧一端固定在墙壁上,另一端与质量m=0.1kg的滑块相连,滑块放置在光滑水平面上。将滑块从弹簧原长位置O向左移至B处并由静止释放,滑块在B、C间往复运动,设弹簧被压缩到B处时具有的弹性势能为5J,则滑块从B运动到O的过程中速度 (选填“A.变大”“B.变小”“C.不变”);滑块运动的最大速度为 m/s,滑块从O到C的过程中滑块与弹簧组成的系统总能量 (选填“A.变大”“B.变小”“C.不变”)。
11.(2024 福建模拟)从地面竖直向上抛出一物体,物体在运动过程中除受到重力外,还受到阻力作用。物体上升、下落过程中动能Ek随高度h的变化的部分图像如图所示。重力加速度取10m/s2。则该物体所受阻力是恒力,大小为 N,该物体的质量为 kg,整个过程损失的机械能是 J。
12.(2024秋 鼓楼区校级月考)如图所示,一根原长为L的轻质弹簧,下端固定在水平桌面上,上端固定一个质量为m的物体A,A静止时弹簧的压缩量为ΔL1,在A上再放一个质量也是m的物体B,待A、B静止后,在B上施加一竖直向下的力F,使弹簧再缩短ΔL2,这时弹簧的弹性势能为Ep。突然撤去力F,则B脱离A向上飞出的瞬间B的速度是 。
四.解答题(共3小题)
13.(2025 乌鲁木齐模拟)如图所示,一辆汽车在平直公路上向左匀速行驶,用长度L=0.4m的轻绳将一质量m=0.2kg的小球悬挂于车厢顶部。将小球向右拉至轻绳与竖直方向成一定夹角时,小球相对于汽车处于静止状态。释放小球,小球连续两次经过最低点时,相对于路面的速度大小分别为v1=22m/s和v2=18m/s,已知重力加速度g取10m/s2,小球可视为质点,忽略空气阻力。求:
(1)释放小球时轻绳与竖直方向的夹角θ;
(2)轻绳对小球拉力的最大值Fm。
14.(2025 仓山区校级模拟)物块A的质量为m=2kg,物块与坡道间的动摩擦因数为μ=0.6,水平面光滑。坡道顶端距水平面高度为h=1m,倾角为θ=37°.物块从坡道进入水平滑道时,在底端O点处无机械能损失,将轻弹簧的一端连接在水平滑道M处并固定墙上,另一自由端恰位于坡道的底端O点,如图所示。物块A从坡顶由静止滑下,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量时的弹性势能;
(3)物块A被弹回到坡道后上升的最大高度。
15.(2024秋 房山区期末)如图所示,光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接,导轨半径为0.40m。一个质量为0.20kg的物体将弹簧压缩至A点后由静止释放,在弹簧弹力作用下,物体脱离弹簧向右运动。经B点沿半圆形导轨运动,到达C点后水平飞出,恰好落在A点。已知B点的速度大小为5.0m/s,A、B两点距离为0.80m,取重力加速度g为10m/s2。求:
(1)物体到达C点的速度大小v。
(2)物体沿半圆形导轨运动过程中阻力所做的功W。
(3)弹簧压缩至A点时的弹性势能Ep。
期末押题预测 机械能守恒定律
参考答案与试题解析
题号 1 2 3 4 5
答案 B B D C C
一.选择题(共5小题)
1.(2025 重庆一模)北京时间2024年11月4日01时24分,神舟十八号载人飞船返回舱在东风着陆场成功着陆。返回舱在打开降落伞后的一段匀速下落过程中,其机械能( )
A.不变 B.减少 C.增加 D.无法确定
【考点】判断机械能是否守恒及如何变化.
【专题】定性思想;推理法;机械能守恒定律应用专题;推理论证能力.
【答案】B
【分析】结合题意,先判断返回舱的动能及重力势能如何变化,即可判断其机械能如何变化,即可分析判断ABCD正误。
【解答】解:因为返回舱在打开降落伞后匀速下落,所以其动能不变,因为返回舱在下落,所以其重力势能减小,因为返回舱的机械能等于其动能与重力势能的和,所以返回舱在打开降落伞后的一段匀速下落过程中,其机械能减少,故B正确,ACD错误;
故选:B。
【点评】本题考查了判断机械能是否守恒及如何变化,解题时需注意,如果除重力或系统内弹力外还有其他力做正功,则系统的机械能增大;如果除重力或系统内弹力外还有其他力做负功,则系统的机械能减小;此类题也可以通过先判断动能与势能如何变化,进而判断机械能如何变化。
2.(2025 福州校级模拟)2024年6月2日至3日,嫦娥六号顺利完成了在月球背面南极—艾特肯盆地的智能快速采样,6月4日7时38分,嫦娥六号上升器携带月球样品自月球背面发射起飞,随后成功进入预定环月轨道,完成世界首次月球背面采样和起飞。已知嫦娥六号质量为m,月球半径为R,以无穷远处为零势能点,嫦娥六号在距月球表面高度为h时的引力势能可表示为(其中G为引力常量,M为月球质量)。若忽略月球的自转,嫦娥六号自月球表面开始发射到进入距离月球表面高度为h的预定环月轨道,至少需要对嫦娥六号做的功为( )
A.
B.
C.
D.
【考点】天体运动中机械能的变化.
【专题】定量思想;推理法;万有引力定律的应用专题;推理论证能力.
【答案】B
【分析】嫦娥六号绕月球做匀速圆周运动,万有引力提供向心力,应用牛顿第二定律求出嫦娥六号的速度,然后应用功能关系求出发生嫦娥六号需要做的功。
【解答】解:根据万有引力提供向心力,得
根据动能表达式,嫦娥六号在环月轨道绕月球做圆周运动的动能
联立以上两式解得
嫦娥六号在h0高度的引力势能为
Ep
在月球表面的引力势能为
根据功能关系,从开始发射到进入预定环月轨道需要对嫦娥六号做的功为
,故ACD错误,B正确。
故选:B。
【点评】本题考查了万有引力定律的应用,根据题意应用牛顿第二定律、功能关系即可解题。
3.(2025 未央区校级模拟)如图所示,一个光滑的固定斜面,倾角θ=30°。劲度系数为k的轻弹簧一端固定在斜面底端,另一端与质量为2m的物体A拴接,另有质量为4m的物体B靠在A上,并施加沿斜面向下的力F=3mg作用在物体B上,系统处于静止。现减小F,使A,B以的加速度一起匀加速向上运动,弹簧始终在弹性限度内,重力加速度为g。则从开始匀加速后到F=0的过程中( )
A.F随位移非均匀变化
B.物体A、B动能增加量为
C.时,物体A、B之间的弹力大小为
D.弹簧弹性势能减小
【考点】常见力做功与相应的能量转化;胡克定律及其应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】D
【分析】根据牛顿第二定律得到F与位移的关系,根据动能定理求解物体A、B动能增加量,对B进行分析得到物体A、B之间的弹力大小,弹性势能变化量的值等于弹簧弹力做功。
【解答】解:A.由题意得,最初A、B静止,根据受力平衡,弹簧弹力大小为
F0=6mgsinθ+3mg=6mg=kx0
当A、B开始匀加速运动,运动位移为x时有
k(x0﹣x)﹣6mgsinθ﹣F=6ma
可得
F=2mg﹣kx
由表达式可知F随位移均匀变化,故A错误;
B.当F = 0时,结合上述有
根据动能定理有
6max=Ek﹣0
结合上述解得
故B错误;
C.对B进行分析,当,有
NAB﹣4mgsinθ﹣F=4ma
结合上述解得
NAB=3mg
故C错误;
D.弹性势能变化量的值等于弹簧弹力做功
故D正确。
故选:D。
【点评】解答本题时,要灵活选择研究对象,采用隔离法和整体法相结合处理,比较简洁。要注意分析弹簧的状态,确定弹力的方向。
4.(2025 浙江)地球和哈雷彗星绕太阳运行的轨迹如图所示,彗星从a运行到b、从c运行到d的过程中,与太阳连线扫过的面积分别为S1和S1,且S1>S2。彗星在近日点与太阳中心的距离约为地球公转轨道半径的0.6倍,则彗星( )
A.在近日点的速度小于地球的速度
B.从b运行到c的过程中动能先增大后减小
C.从a运行到b的时间大于从c运行到d的时间
D.在近日点加速度约为地球的加速度的0.36倍
【考点】天体运动中机械能的变化;开普勒三大定律.
【专题】定量思想;推理法;万有引力定律在天体运动中的应用专题;推理论证能力.
【答案】C
【分析】根据高轨低速大周期的二级结论分析;根据万有引力做功情况分析;根据开普勒第二定律分析;根据牛顿第二定律分析。
【解答】解:A、假设彗星以0.6r绕太阳做匀速圆周运动为轨道1速度为v1,地球绕太阳做圆周运动为轨道3环绕速度为v3,根据高轨低速的推论,可知v1>3,如果彗星从轨道1变为原本的椭圆轨道(设为轨道2),要做离心运动,需要在近地点瞬间加速,则彗星在原本椭圆轨道近日点的速度,v2>v1,综上所述,v2>v3,即彗星在近日点的速度大于地球的速度,故A错误;
B、彗星从b运行到c的过程中,万有引力一直做负功,动能一直减小,故B错误;
C、根据开普勒第二定律,可知彗星从a运行到b的时间大于从c到a的运行时间,故C正确;
D、对于地球绕太阳的匀速圆周运动,设环绕半径为r,根据牛顿第二定律,解得;对于彗星在近日点,根据牛顿第二第二定律有,解得a,故D错误。
故选:C。
【点评】本题考查了万有引力定律和开普勒定律在天体运动中的应用问题,记住二级结论高轨低速大周期可以快速判断。
5.(2025 雨花区校级开学)如图所示,绕过定滑轮1、2的轻质细线一端吊着小球A,另一端连接可视为质点的物块B,物AC块B放在光滑水平面上,此时细线处于伸直状态。现将小球A由静止释放,至物块B沿水平岛面运动到定滑轮2正下方的过程中(不计滑轮的大小、质量和摩擦,物块B运动到滑轮2正下方时,小球A还未落地),下列说法正确的是( )
A.小球A和物块B的速率始终相等
B.小球A先超重后失重
C.小球A的合力先做正功后做负功
D.小球A的机械能先增大后减小
【考点】机械能守恒定律的简单应用;关联速度问题;功的正负及判断.
【专题】比较思想;合成分解法;机械能守恒定律应用专题;理解能力.
【答案】C
【分析】根据物块B沿细线方向的分速度大小与小球A的速度大小相等,分析小球A和物块B的速率是否相等;根据开始时与B运动到滑轮2的正下方时小球A的速度分析A的运动情况,再判断其运动状态;根据动能定理分析小球A的合力做功情况;根据细线拉力对小球A做功情况,分析小球A的机械能变化情况。
【解答】解:A、物块B沿细线方向的分速度大小与小球A的速度大小始终相等,故A错误;
B、开始时,小球A的速度为零。当物块B运动到滑轮2的正下方时,小球A的速度也为零,所以小球A向下先加速后减速到速度为零,加速度先向下后向上,先失重后超重,故B错误;
C、小球A的动能先增大后减小,根据动能定理可知,小球A的合力先做正功后做负功,故C正确;
D、细线对小球A的拉力一直做负功,所以小球A的机械能一直减少,故D错误。
故选:C。
【点评】本题是牵连速度问题,要知道物块B沿细线方向的分速度大小与小球A的速度大小始终相等,当当物块B运动到滑轮2的正下方时,小球A的速度为零,来分析A的运动情况,判断合力做功情况。
二.多选题(共4小题)
(多选)6.(2025 城关区校级开学)如图所示的传送带由水平部分和倾斜部分组成,倾斜部分与水平方向的夹角为37°。传送带以某一速度按图示方向运转,t=0时,将一质量为m=1kg的小滑块轻放在传送带的最顶端,以后滑块的速度大小与时间的变化关系如图所示,t=2.2s时滑块刚好到达最右端,物块在两传送带交接处运动时无机械能损失,重力加速度g=10m/s2,下列说法正确的是( )
A.滑块与传送带间的动摩擦因数为μ=0.6
B.滑块运动过程中能够达到的最大速度为vm=8m/s
C.传送带水平部分的总长度为l=3.6m
D.从t=0到t=0.6s的过程中,电动机额外提供电能E=14.4J
【考点】常见力做功与相应的能量转化;复杂的运动学图像问题;牛顿第二定律的简单应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】BD
【分析】A.从t=0到t=0.6s的过程中,结合题图及牛顿第二定律分别列式,即可分析判断;
B.从t=0.6s到t=1.6s过程中,结合题图,根据牛顿第二定律、匀变速直线运动规律分别列式,即可分析判断;
C.结合前面分析,由运动学规律分别列式,即可分析判断;
D.结合前面分析,从t=0到t=0.6s的过程中,根据功能关系及运动学规律分别列式,即可分析判断。
【解答】解:A.由图可知,从t=0到t=0.6s的过程中,物块在倾斜传送带上做加速运动,当t=0.6s时物块与传送带共速,均为6m/s,
则该过程加速度大小为:,
根据牛顿第二定律可得:mgsin37°+μmgcos37°=ma1,
联立可得:μ=0.5,
故A错误;
B.由图可知,t=0.6s到t=1.6s过程中,物块在倾斜传送带上继续加速,但由于物块速度大于传送带速度,
根据牛顿第二定律可得:mgsin37°﹣μmgcos37°=ma2,
再结合匀变速直线运动规律可得:vm﹣v1=a2t2,
其中:v1=6m/s,t2=1.6s﹣0.6s=1s,
联立可得:vm=8m/s,
故B正确;
C.结合前面分析可知,当滑块在水平传送带上减速时,
有:vm﹣v1=μgΔt,
解得:Δt=0.4s,
传送带水平部分长度为:lv1(0.6s﹣Δt),
联立可得:l=4m,
故C错误;
D.结合前面分析可知,从t=0到t=0.6s的过程中,根据功能关系可知,
电动机额外提供电能为:E=μmgcosθ x1,
其中:x1=v1t=6×0.6m=3.6m,
联立可得:E=14.4J,
故D正确;
故选:BD。
【点评】本题主要考查对牛顿第二定律的掌握,解题时需注意,应用牛顿第二定律解决简单问题时,要先明确物体的受力情况,然后列出牛顿第二定律的表达式,再根据需要求出相关物理量。
(多选)7.(2025 高新区校级模拟)如图所示,在竖直平面直角坐标系xOy中,在t=0时,质量m=0.5kg的小球从坐标原点O处,以初速度斜向右上方抛出,同时受到F风=5N的作用(虚线箭头为风力方向与v0的夹角为30°,且与x轴正方向的夹角也为30°),重力加速度g取10m/s2。下列说法正确的是( )
A.小球的加速度先增大后减小
B.小球在t=0.6s时再次经过x轴
C.小球的重力势能一直减小
D.小球的动能一直增大
【考点】常见力做功与相应的能量转化;斜抛运动.
【专题】定量思想;推理法;平抛运动专题;推理论证能力.
【答案】BD
【分析】由题意和几何知识可知小球受到的合力与初速度的方向垂直,小球做类平抛运动,结合牛顿第二定律以及运动学公式分析。
【解答】解:A.由题意和几何知识可知小球受到的合力为
F=5N
方向与初速度的方向垂直,小球做类平抛运动,小球的加速度不变,故A错误;
B.小球再次经过x轴时,沿初速度方向的位移和垂直初速度的位移关系为
又
解得
t=0.6s
故B正确;
C.小球做类平抛运动,小球的高度先增加后减小,重力势能先增加后减小,故C错误;
D.小球做类平抛运动,速度一直在增加,小球的动能一直增大,故D正确。
故选:BD。
【点评】本题解题关键是分析出小球受到的合力与初速度的方向垂直,小球做类平抛运动。
(多选)8.(2025 兰州校级一模)如图甲所示,斜面倾角为α=30°、足够长、光滑的斜面体固定在水平地面上,可视为质点的质量为m=4kg的物块置于斜面上足够高处,t=0时刻在物块上施加一沿斜面向上的变化的外力,同时释放物块,利用计算机描绘了0~4s时间内物块的速度随时间的变化图象,如图乙所示,规定沿斜面向下的方向为正方向,物块在释放点的重力势能为零,重力加速度大小为g=10m/s2。则( )
A.1~2s的时间内外力的大小为40N
B.0~1s时间内与2~4s时间内的外力大小之比为2:19
C.1s末物块的机械能为32J
D.0~4s的时间内物块的机械能减少了350J
【考点】常见力做功与相应的能量转化;牛顿第二定律的简单应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】BD
【分析】v﹣t图像斜率表示加速度,v﹣t图像面积表示位移,结合牛顿第二定律求解拉力F大小,物块机械能的变化量等于整个过程外力F所做的功,外力F所做的功等于力与位移乘积。
【解答】解:A.由图乙可知,1s~2s时内物块的加速度为
位移大小为
由牛顿第二定律得
mgsin30°﹣F2=ma2
解得
F2=0
故A错误;
B.由图乙可知,0 1s时内物块的加速度为
位移大小为
由牛顿第二定律得
mgsin30°﹣F1=ma1
解得
F1=4N
由图乙可知,2s~4s时内物块的加速度为
位移大小为
由牛顿第二定律得
mgsin30°﹣F3=ma3
解得
F3=38N
则
F1:F3=2:19
故B正确;
CD.由题意可知,t=0时刻,物块的机械能为0,由功能关系可知,物块机械能的变化量等于整个过程外力F所做的功,0 1s外力做的功为
W1=F1x1=﹣4×2J=﹣8J
即1s末物块的机械能为﹣8J,2s~4s外力做的功为
W3=F3x3=﹣38×9J=﹣342J
则整个过程中物块机械能变化量大小为
ΔE=|W1+W3|=350J
故C错误,D正确。
故选:BD。
【点评】解题关键是知道v﹣t图像的面积等于位移,v﹣t图像的斜率表示加速度。
(多选)9.(2024秋 郴州期末)如图所示,一劲度系数为k=1N/cm的轻质弹簧左端固定在竖直墙壁上,弹簧右端固定有一质量为m=2kg的物块,物块与水平地面间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力。用力向左推动物块使弹簧压缩量达到x1=11cm后由静止释放物块,重力加速度g=10m/s2,不计空气阻力,下列说法正确的是( )
A.释放后瞬间物块的加速度大小为5m/s2
B.物块第一次向右运动的最大距离为18cm
C.物块最终停在弹簧的原长左侧1cm处
D.物块从静止释放,到最终停下,整个过程中因摩擦而产生的内能为0.56J
【考点】常见力做功与相应的能量转化;牛顿第二定律的简单应用.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】BC
【分析】由牛顿第二定律求解加速度,向右运动的最大位移和释放点关于该平衡位置对称,物块向左运动的过程中,求解新的平衡位置,摩擦产生的热量等于摩擦力乘以相对位移。
【解答】解:质量为m=2kg的物块,物块与水平地面间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力,劲度系数为k=1N/cm的轻质弹簧
由牛顿第二定律
kx1﹣μmg=ma
得加速度
a=4.5m/s2
平衡位置为
kx2=μmg
x2=2cm
向右运动的最大位移和释放点关于该平衡位置对称,所以物块第一次向右运动的最大距离为18cm;物块向左运动的过程中,在新的平衡位置
kx3=μmg
x3=x2=2cm
所以物块向左运动10cm,以此类推,物块第二次向右运动2cm后停下来,所以物块停在距离弹簧原长左侧1cm处,总路程为30cm,从而摩擦产生的热量为
Q=μmgs=0.1×20×0.3J=0.6J,故AD错误,BC正确。
故选:BC。
【点评】物体向一个方向运动时,摩擦力恒定,可以看成在摩擦力和弹力共同作用下的简谐运动。
三.填空题(共3小题)
10.(2024秋 思明区校级月考)如图,轻质弹簧一端固定在墙壁上,另一端与质量m=0.1kg的滑块相连,滑块放置在光滑水平面上。将滑块从弹簧原长位置O向左移至B处并由静止释放,滑块在B、C间往复运动,设弹簧被压缩到B处时具有的弹性势能为5J,则滑块从B运动到O的过程中速度 变大 (选填“A.变大”“B.变小”“C.不变”);滑块运动的最大速度为 10 m/s,滑块从O到C的过程中滑块与弹簧组成的系统总能量 不变 (选填“A.变大”“B.变小”“C.不变”)。
【考点】弹簧类问题中的机械能守恒.
【专题】定量思想;推理法;机械能守恒定律应用专题;推理论证能力.
【答案】变大;10;不变
【分析】根据机械能守恒定律分析能量变化,从而分析最大速度的位置,根据机械能守恒定律列式计算最大速度。
【解答】解:滑块从B运动到O的过程中,弹簧弹性势能减小,动能增大,则速度变大,则O点的速度最大,根据机械能守恒定律有
Ep
解得v=10m/s
根据机械能守恒定律可知,滑块从O到C的过程中滑块与弹簧组成的系统总能量不变。
故答案为:变大;10;不变
【点评】本题关键是明确机械能守恒定律答应用,解题关键掌握能量的转化特点。
11.(2024 福建模拟)从地面竖直向上抛出一物体,物体在运动过程中除受到重力外,还受到阻力作用。物体上升、下落过程中动能Ek随高度h的变化的部分图像如图所示。重力加速度取10m/s2。则该物体所受阻力是恒力,大小为 2 N,该物体的质量为 1 kg,整个过程损失的机械能是 24 J。
【考点】机械能与图像相结合的问题.
【专题】定量思想;推理法;机械能守恒定律应用专题;分析综合能力.
【答案】2;1;24。
【分析】Ek﹣h图象的斜率大小等于物体受到的合力,根据斜率可以求出物体的质量和所受阻力;根据动能定理可求物体上升的最大高度,整个过程应用功能关系求出机械能的损失。
【解答】解:Ek﹣h图象的斜率大小等于物体受到的合力,上升过程和下降过程的斜率不变,说明阻力是恒力,设空气阻力为F,则上升过程有:
下落过程有
联立解得
m=1kg,F=2N,
设物体上升的最大高度为H,由动能定理得
(mg+F)H=Ek0
解得
H=6m,
整个过程损失的机械能等于克服阻力做的功
ΔE=F×2H
解得
ΔE=24J
故答案为:2;1;24。
【点评】解决该题的关键是明确图象中斜率的大小表示的是物体受到的合外力,知道上升和下降过程中合外力的表达式。知道机械能的变化等于除重力外其它力做的功。
12.(2024秋 鼓楼区校级月考)如图所示,一根原长为L的轻质弹簧,下端固定在水平桌面上,上端固定一个质量为m的物体A,A静止时弹簧的压缩量为ΔL1,在A上再放一个质量也是m的物体B,待A、B静止后,在B上施加一竖直向下的力F,使弹簧再缩短ΔL2,这时弹簧的弹性势能为Ep。突然撤去力F,则B脱离A向上飞出的瞬间B的速度是 。
【考点】弹簧类问题中的机械能守恒.
【专题】定量思想;方程法;机械能守恒定律应用专题;推理论证能力.
【答案】。
【分析】分离瞬间加速度相同,相互作用力为零,整个运动过程中系统机械能守恒,根据机械能守恒定律即可求解。
【解答】解:分离瞬间加速度相同,相互作用力为零,从撤除力到A、B分离,系统机械能守恒,则有:Ep=2mg(2ΔL1+ΔL2) 2mv2
解得:v。
故答案为:。
【点评】本题主要考查了械能守恒定律的应用,知道在分离的瞬间,AB加速度相同,之间的作用力为零。
四.解答题(共3小题)
13.(2025 乌鲁木齐模拟)如图所示,一辆汽车在平直公路上向左匀速行驶,用长度L=0.4m的轻绳将一质量m=0.2kg的小球悬挂于车厢顶部。将小球向右拉至轻绳与竖直方向成一定夹角时,小球相对于汽车处于静止状态。释放小球,小球连续两次经过最低点时,相对于路面的速度大小分别为v1=22m/s和v2=18m/s,已知重力加速度g取10m/s2,小球可视为质点,忽略空气阻力。求:
(1)释放小球时轻绳与竖直方向的夹角θ;
(2)轻绳对小球拉力的最大值Fm。
【考点】机械能守恒定律的简单应用;牛顿第二定律的简单应用;牛顿第二定律与向心力结合解决问题.
【专题】计算题;定量思想;寻找守恒量法;机械能守恒定律应用专题;分析综合能力.
【答案】(1)释放小球时轻绳与竖直方向的夹角θ为60°;
(2)轻绳对小球拉力的最大值Fm为4N。
【分析】(1)设车的速度大小为v车,小球运动过程中相对于车的最大速度为vm,当小球向左经过最低点时,有v1=v车+vm;当小球向右经过最低点时,有v2=v车﹣vm,由此求出vm。再以车厢为参考系,根据机械能守恒定律求释放小球时轻绳与竖直方向的夹角θ;
(2)小球经过最低点时,根据牛顿第二定律求解轻绳对小球拉力的最大值Fm。
【解答】解:(1)取向左为正方向,设车的速度大小为v车,小球运动过程中相对于车的最大速度为vm。
小球向左经过最低点时的速度v1=v车+vm
小球向右经过最低点时的速度v2=v车﹣vm
解得
vm=2m/s
以车厢为参考系,小球由释放至运动到最低点的过程中,根据机械能守恒定律有
mgL(1﹣cosθ)
解得θ=60°
(2)小球经过最低点时,根据牛顿第二定律有
Fm﹣mg=m
解得Fm=4N
答:(1)释放小球时轻绳与竖直方向的夹角θ为60°;
(2)轻绳对小球拉力的最大值Fm为4N。
【点评】解答本题时,要理解运动的相对性,要知道匀速运动的参考系与静止参考系遵守相同的物理规律。
14.(2025 仓山区校级模拟)物块A的质量为m=2kg,物块与坡道间的动摩擦因数为μ=0.6,水平面光滑。坡道顶端距水平面高度为h=1m,倾角为θ=37°.物块从坡道进入水平滑道时,在底端O点处无机械能损失,将轻弹簧的一端连接在水平滑道M处并固定墙上,另一自由端恰位于坡道的底端O点,如图所示。物块A从坡顶由静止滑下,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量时的弹性势能;
(3)物块A被弹回到坡道后上升的最大高度。
【考点】弹簧类问题中的机械能守恒;动能定理的简单应用.
【专题】计算题;定性思想;推理法;动能定理的应用专题;机械能守恒定律应用专题;理解能力.
【答案】见试题解答内容
【分析】(1)物块A从坡顶滑下,重力和摩擦力做功,根据动能定理可求出物块滑到O点时的速度大小。
(2)物块压缩弹簧后,物块和弹簧组成的系统机械能守恒,根据机械能守恒定律可弹性势能。
(3)物块滑回到O点时与刚滑到O点时速度大小相等,从坡底到坡顶,再动能定理求解最大高度。
【解答】解:(1)由动能定理得:
解得:,
代入数据得:v=2m/s
(2)在水平滑道上,由机械能守恒定律得:mv2=Ep
代入数据得:Ep=4J
(3)设物块A能够上升的最大高度为h1,物块被弹回过程中由动能定理得:
代入数据解得:h1m
答:(1)物块滑到O点时的速度大小是2m/s。
(2)弹簧为最大压缩量时的弹性势能为4J。
(3)物块A被弹回到坡道后上升的最大高度是m。
【点评】本题是动能定理与机械能守恒定律的简单运用。对动能定理的运用,要选择研究过程,分析哪些力对物体做功,进而确定合力的功或总功。
15.(2024秋 房山区期末)如图所示,光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接,导轨半径为0.40m。一个质量为0.20kg的物体将弹簧压缩至A点后由静止释放,在弹簧弹力作用下,物体脱离弹簧向右运动。经B点沿半圆形导轨运动,到达C点后水平飞出,恰好落在A点。已知B点的速度大小为5.0m/s,A、B两点距离为0.80m,取重力加速度g为10m/s2。求:
(1)物体到达C点的速度大小v。
(2)物体沿半圆形导轨运动过程中阻力所做的功W。
(3)弹簧压缩至A点时的弹性势能Ep。
【考点】多物体系统的机械能守恒问题;平抛运动速度的计算;动能定理的简单应用;弹簧类问题中的机械能守恒.
【专题】定量思想;推理法;平抛运动专题;动能定理的应用专题;机械能守恒定律应用专题;推理论证能力.
【答案】(1)物体到达C点的速度大小v为2m/s;
(2)物体沿半圆形导轨运动过程中阻力所做的功W为﹣0.5J;
(3)弹簧压缩至A点时的弹性势能Ep为2.5J。
【分析】(1)物体由C到A做平抛运动,由平抛运动的运动规律分别列式,即可分析求解;
(2)物体沿半圆形导轨运动过程中,由动能定理列式,即可分析求解;
(3)释放物体的过程,由机械能守恒定律列式,即可分析求解。
【解答】解:(1)物体由C到A做平抛运动,由平抛运动的运动规律可知,
水平方向有:xBA=vt,
竖直方向有:2Rgt2,
由题知:xBA=0.80m,R=0.40m,
联立可得:v=2m/s;
(2)物体沿半圆形导轨运动过程中,
由动能定理可得:﹣mg 2R+W,
由题知:m=0.20kg,vB=5.0m/s,
解得:W=﹣0.5J;
(3)释放物体的过程,弹簧与物体组成的系统机械能守恒,可得:Ep,
解得:Ep=2.5J;
答:(1)物体到达C点的速度大小v为2m/s;
(2)物体沿半圆形导轨运动过程中阻力所做的功W为﹣0.5J;
(3)弹簧压缩至A点时的弹性势能Ep为2.5J。
【点评】本题主要考查多物体系统的机械能守恒问题,解题时需注意,在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
