【期末押题预测】向心加速度(含解析)2024-2025学年高中物理人教版(2019)高一下册
文档属性
| 名称 | 【期末押题预测】向心加速度(含解析)2024-2025学年高中物理人教版(2019)高一下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-27 15:23:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末押题预测 向心加速度
一.选择题(共5小题)
1.(2024秋 杨浦区校级期末)如图所示,同学们组成的跑操方阵排列整齐地匀速率通过圆弧形跑道区域,每个方阵中的每位同学均可视为做匀速圆周运动。则下列说法正确的是( )
A.每位同学的角速度相同
B.每位同学所受的合力为零
C.每位同学的速度大小相同
D.每位同学的加速度保持不变
2.(2024秋 道里区校级期末)如图所示、甲、乙两位同学握住绳子A、B两端摇动,A、B两端近似不动,且A、B两点连线沿水平方向,绳子上P、Q等各点均同步在竖直面做匀速圆周运动。当绳子在空中转到如图所示位置时,则( )
A.P点的线速度方向沿绳子切线
B.P点所受合外力垂直于绳斜向下
C.P点和Q点的线速度大小相等
D.P点的角速度等于Q点的角速度
3.(2024秋 朝阳区校级期末)如图所示,在长春市人民广场转盘,A、B两车正在水平圆形车道上做线速度大小相等的匀速圆周运动,下列说法正确的是( )
A.A车的角速度比B车的角速度小
B.A车的角速度比B车的角速度大
C.A车的向心加速度小于B车的向心加速度
D.A车的向心加速度等于B车的向心加速度
4.(2024秋 宁波期末)如图为修正带的内部结构,由大小两个相互咬合的齿轮组成,修正带芯固定在大齿轮的转轴上。当按压并拖动其头部时,齿轮转动,从而将遮盖物质均匀地涂抹在需要修改的字迹上。若图中大小齿轮的半径之比为2:1,A、B分别为大齿轮和小齿轮边缘上的一点,C为大齿轮上转轴半径的中点,则( )
A.A与B的角速度大小之比为1:2 B.B与C的线速度大小之比为1:1
C.A与C的向心加速度大小之比为4:1 D.大小齿轮的转动方向相同
5.(2024秋 龙岗区期末)脚踏车上的飞轮传动系统如图所示,设各轮的转轴均固定且相互平行,甲、乙两轮同轴且无相对转动,已知甲、乙、丙、丁四轮的半径比为5:2:3:1,A、B分别是甲、乙两轮边缘上的点,两传送带在四轮转动时均不打滑,下列判断正确的是( )
A.甲、乙两轮的角速度相等
B.A点向心加速度比B点的小
C.两传送带的线速度大小相等
D.当丙轮转1圈时,丁轮已转10圈
二.多选题(共4小题)
(多选)6.(2023秋 长沙校级期末)图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点。左侧是一轮轴,大轮的半径为4r,小轮的半径为2r。b点在小轮上,到小轮中心的距离为r。c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑。则( )
A.a点与b点的线速度大小之比为2:1
B.a点与b点的角速度大小之比2:1
C.a点与c点的线速度大小之比1:1
D.a点的向心加速度与d点的向心加速度之比2:1
(多选)7.(2024 江西模拟)陶瓷是中华瑰宝,是中华文明的重要名片。在陶瓷制作过程中有一道工序叫利坯,如图(a)所示,将陶瓷粗坯固定在绕竖直轴转动的水平转台上,用刀旋削,使坯体厚度适当,表里光洁。对应的简化模型如图(b)所示,粗坯的对称轴与转台转轴OO′重合。当转台转速恒定时,关于粗坯上P、Q两质点,下列说法正确的是( )
A.P的角速度大小比Q的大
B.P的线速度大小比Q的大
C.P的向心加速度大小比Q的大
D.同一时刻P所受合力的方向与Q的相同
(多选)8.(2023秋 黔西南州期末)做匀速圆周运动的物体,10s内在沿半径为10m的圆周上运动了200m,则物体做匀速圆周运动时( )
A.周期为2πs
B.线速度的大小为20m/s
C.角速度的大小为2rad/s
D.向心加速度大小为20m/s2
(多选)9.(2023秋 泰安期末)如图所示,自行车的小齿轮A、大齿轮B、后轮C的半径之比为1:3:9,在用力蹬脚踏板前进的过程中,下列说法正确的是( )
A.小齿轮A与后轮C的角速度大小之比为9:1
B.小齿轮A与大齿轮B的角速度大小之比为3:1
C.后轮C边缘与大齿轮B边缘各点的线速度大小之比为9:1
D.大齿轮B边缘与小齿轮A边缘各点的向心加速度大小之比为3:1
三.填空题(共3小题)
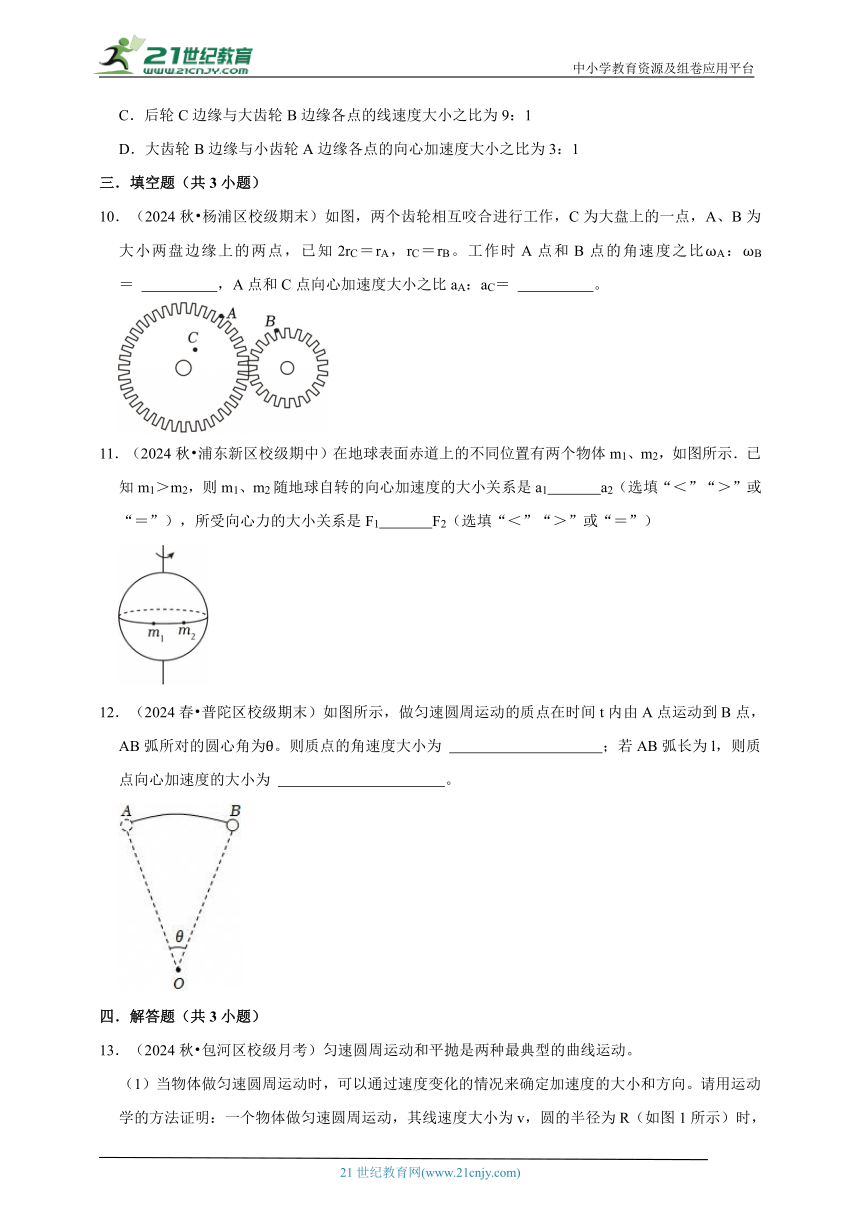
10.(2024秋 杨浦区校级期末)如图,两个齿轮相互咬合进行工作,C为大盘上的一点,A、B为大小两盘边缘上的两点,已知2rC=rA,rC=rB。工作时A点和B点的角速度之比ωA:ωB= ,A点和C点向心加速度大小之比aA:aC= 。
11.(2024秋 浦东新区校级期中)在地球表面赤道上的不同位置有两个物体m1、m2,如图所示.已知m1>m2,则m1、m2随地球自转的向心加速度的大小关系是a1 a2(选填“<”“>”或“=”),所受向心力的大小关系是F1 F2(选填“<”“>”或“=”)
12.(2024春 普陀区校级期末)如图所示,做匀速圆周运动的质点在时间t内由A点运动到B点,AB弧所对的圆心角为θ。则质点的角速度大小为 ;若AB弧长为l,则质点向心加速度的大小为 。
四.解答题(共3小题)
13.(2024秋 包河区校级月考)匀速圆周运动和平抛是两种最典型的曲线运动。
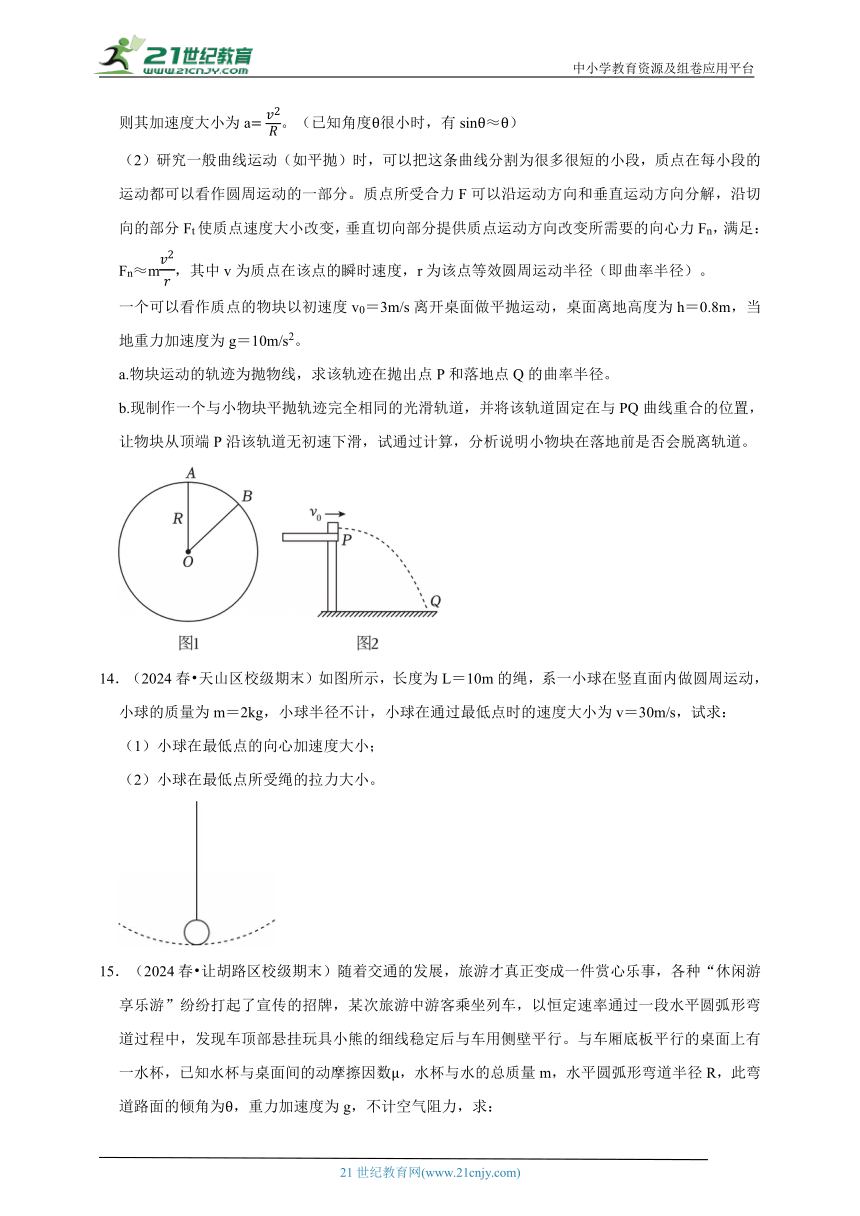
(1)当物体做匀速圆周运动时,可以通过速度变化的情况来确定加速度的大小和方向。请用运动学的方法证明:一个物体做匀速圆周运动,其线速度大小为v,圆的半径为R(如图1所示)时,则其加速度大小为a。(已知角度θ很小时,有sinθ≈θ)
(2)研究一般曲线运动(如平抛)时,可以把这条曲线分割为很多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。质点所受合力F可以沿运动方向和垂直运动方向分解,沿切向的部分Ft使质点速度大小改变,垂直切向部分提供质点运动方向改变所需要的向心力Fn,满足:Fn≈m,其中v为质点在该点的瞬时速度,r为该点等效圆周运动半径(即曲率半径)。
一个可以看作质点的物块以初速度v0=3m/s离开桌面做平抛运动,桌面离地高度为h=0.8m,当地重力加速度为g=10m/s2。
a.物块运动的轨迹为抛物线,求该轨迹在抛出点P和落地点Q的曲率半径。
b.现制作一个与小物块平抛轨迹完全相同的光滑轨道,并将该轨道固定在与PQ曲线重合的位置,让物块从顶端P沿该轨道无初速下滑,试通过计算,分析说明小物块在落地前是否会脱离轨道。
14.(2024春 天山区校级期末)如图所示,长度为L=10m的绳,系一小球在竖直面内做圆周运动,小球的质量为m=2kg,小球半径不计,小球在通过最低点时的速度大小为v=30m/s,试求:
(1)小球在最低点的向心加速度大小;
(2)小球在最低点所受绳的拉力大小。
15.(2024春 让胡路区校级期末)随着交通的发展,旅游才真正变成一件赏心乐事,各种“休闲游享乐游”纷纷打起了宣传的招牌,某次旅游中游客乘坐列车,以恒定速率通过一段水平圆弧形弯道过程中,发现车顶部悬挂玩具小熊的细线稳定后与车用侧壁平行。与车厢底板平行的桌面上有一水杯,已知水杯与桌面间的动摩擦因数μ,水杯与水的总质量m,水平圆弧形弯道半径R,此弯道路面的倾角为θ,重力加速度为g,不计空气阻力,求:
(1)列车转弯过程中的向心加速度大小;
(2)列车转弯过程中,水杯与桌面间的摩擦力。
期末押题预测 向心加速度
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 杨浦区校级期末)如图所示,同学们组成的跑操方阵排列整齐地匀速率通过圆弧形跑道区域,每个方阵中的每位同学均可视为做匀速圆周运动。则下列说法正确的是( )
A.每位同学的角速度相同
B.每位同学所受的合力为零
C.每位同学的速度大小相同
D.每位同学的加速度保持不变
【考点】向心加速度的概念、方向及物理意义;匀速圆周运动;线速度与角速度的关系.
【专题】定性思想;推理法;匀速圆周运动专题;理解能力.
【答案】A
【分析】根据匀速圆周运动的特点:绕同一圆心做圆周运动其角速度相同,线速度v=ωr判定线速度,合外力提供向心力,加速度始终指向圆心。
【解答】解:A.每个方阵中的每位同学均可视为绕同一圆心做匀速圆周运动,则角速度相同。故A正确;
B.每位同学均做匀速圆周运动,所受的合力提供向心力,合力不为零。故B错误;
C.根据v=ωr可知每位同学的运动半径不同,其速度大小不相同。故C错误;
D.根据a=ω2r可知每位同学的加速度大小保持不变,方向指向圆心,时刻改变。故D错误。
故选:A。
【点评】本题主要考查了匀速圆周运动的特点,解题关键是掌握绕同一圆心做圆周运动其角速度相同,线速度v=ωr判定线速度,合外力提供向心力,加速度始终指向圆心。
2.(2024秋 道里区校级期末)如图所示、甲、乙两位同学握住绳子A、B两端摇动,A、B两端近似不动,且A、B两点连线沿水平方向,绳子上P、Q等各点均同步在竖直面做匀速圆周运动。当绳子在空中转到如图所示位置时,则( )
A.P点的线速度方向沿绳子切线
B.P点所受合外力垂直于绳斜向下
C.P点和Q点的线速度大小相等
D.P点的角速度等于Q点的角速度
【考点】向心加速度的计算;线速度与角速度的关系.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】D
【分析】AB.根据题意分析P点的圆周平面,判断P点的合外力方向和速度方向;
CD.根据共轴转动情况判断角速度关系,结合半径差异判断线速度大小关系。
【解答】解:AB.P点做匀速圆周运动的圆心是过P点作图中虚线的垂线和虚线的交点,故P点所受合力方向指向交点,方向竖直向下,P点线速度方向为垂直于纸面向里或向外,故AB错误;
CD.由于是共轴转动,故P点的角速度等于Q点的角速度,P点圆周运动半径小于Q点,则P点线速度大小小于Q点的线速度大小,故C错误,D正确。
故选:D。
【点评】考查圆周运动的合外力和线速度规律,结合共轴转动问题判断线速度大小关系。
3.(2024秋 朝阳区校级期末)如图所示,在长春市人民广场转盘,A、B两车正在水平圆形车道上做线速度大小相等的匀速圆周运动,下列说法正确的是( )
A.A车的角速度比B车的角速度小
B.A车的角速度比B车的角速度大
C.A车的向心加速度小于B车的向心加速度
D.A车的向心加速度等于B车的向心加速度
【考点】向心加速度的计算;线速度与角速度的关系.
【专题】比较思想;归纳法;匀速圆周运动专题;理解能力.
【答案】B
【分析】根据分析角速度的大小;根据a分析向心加速度的大小。
【解答】解:AB、由图知A的半径小于B的半径,根据可知,A的角速度大于B的角速度,故A错误,B正确;
CD、根据a可知,A车的向心加速度大于B车的向心加速度,故CD错误。
故选:B。
【点评】本题考查了角速度和线速度的关系,以及向心加速度和线速度的关系式,容易题。
4.(2024秋 宁波期末)如图为修正带的内部结构,由大小两个相互咬合的齿轮组成,修正带芯固定在大齿轮的转轴上。当按压并拖动其头部时,齿轮转动,从而将遮盖物质均匀地涂抹在需要修改的字迹上。若图中大小齿轮的半径之比为2:1,A、B分别为大齿轮和小齿轮边缘上的一点,C为大齿轮上转轴半径的中点,则( )
A.A与B的角速度大小之比为1:2
B.B与C的线速度大小之比为1:1
C.A与C的向心加速度大小之比为4:1
D.大小齿轮的转动方向相同
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;角速度、周期、频率与转速的关系及计算;传动问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】A
【分析】同缘传动时,边缘点的线速度相等;同轴传动时,角速度相等;然后结合v=ωr列式求解。
【解答】解:ABC.边缘点的线速度大小相等,故vA:vB=1:1,同轴传动时,角速度相等,故ωA=ωC,角速度大小之比为1:1,根据v=ωr,结合半径的比值关系:rA:rB:rC=2:1:1。可知,ωA:ωB:ωC=1:2:1,vA:vB:vC=2:2:1;向心加速度的表达式可得:a=ω2r解得:aA:aB:aC=2:4:1,故A正确,BC错误;
D、大、小齿轮相互咬合,同缘传动时,大、小齿轮转动方向相反,故D错误;
故选:A。
【点评】本题关键明确同缘传动同轴传动的特点:同轴传动时,角速度相等,同缘传动时,边缘点的线速度相等,然后结合公式v=ωr分析求解即可。
5.(2024秋 龙岗区期末)脚踏车上的飞轮传动系统如图所示,设各轮的转轴均固定且相互平行,甲、乙两轮同轴且无相对转动,已知甲、乙、丙、丁四轮的半径比为5:2:3:1,A、B分别是甲、乙两轮边缘上的点,两传送带在四轮转动时均不打滑,下列判断正确的是( )
A.甲、乙两轮的角速度相等
B.A点向心加速度比B点的小
C.两传送带的线速度大小相等
D.当丙轮转1圈时,丁轮已转10圈
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;传动问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】A
【分析】各轮转轴固定且平行,甲、乙两轮同轴无相对转动,意味着甲、乙两轮角速度相等,甲、乙、丙、丁四轮半径之比为5:2:3:1,且传送带不打滑,说明与轮子接触处传送带线速度和轮子边缘线速度相等,据此分析解答即可。
【解答】解:A.因为甲、乙两轮同轴无相对转动,根据同轴转动的物体角速度相等这一特性,所以甲、乙两轮的角速度相等,故A正确。
B.根据向心加速度公式a = ω2r,甲、乙两轮角速度ω相等,A点在甲轮边缘,B点在乙轮边缘,甲轮半径大于乙轮半径,所以A点向心加速度比B点的大,故B错误。
CD.设甲轮半径r甲=5r,乙轮半径r乙=2r,丙轮半径r丙=3r,丁轮半径r丁=r,由于甲、乙两轮角速度相等,设为ω,则甲轮边缘线速度为
v甲=ωr甲
解得:v甲=5rω,
乙轮边缘线速度为
v乙=ωr乙
解得:v乙=2rω
根据同一传动装置接触边缘的线速度大小是相等及v= ωr得:
ω丙
联立解得:
所以丙轮转1圈时,丁轮转了圈,两传送带线速度大小不相等,故CD错误。
故选:A。
【点评】本题考查了线速度与角速度关系,知道共轴的角速度是相同的,同一传动装置接触边缘的线速度大小是相等的,注意灵活应用线速度、角速度与半径之间的关系.
二.多选题(共4小题)
(多选)6.(2023秋 长沙校级期末)图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点。左侧是一轮轴,大轮的半径为4r,小轮的半径为2r。b点在小轮上,到小轮中心的距离为r。c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑。则( )
A.a点与b点的线速度大小之比为2:1
B.a点与b点的角速度大小之比2:1
C.a点与c点的线速度大小之比1:1
D.a点的向心加速度与d点的向心加速度之比2:1
【考点】向心加速度的表达式及影响向心加速度大小的因素;传动问题.
【专题】定量思想;比例法;匀速圆周运动专题;理解能力.
【答案】ABC
【分析】右轮与左侧小轮的线速度相等,左侧大轮与小轮的角速度相等,根据圆周运动公式分析。
【解答】解:C.如图所示,a与c同一皮带下传动,则线速度va=vc,故C正确;
AB.根据v=ωr,可得ωa:ωc=rc:ra=2:1,因为ωb=ωc=ωd,且rb:rc=1:2,所以vb:vc=1:2,则va:vb=2:1,ωa:ωb=2:1,故AB正确;
D.设a点的线速度为v,由以上分析可知,c点的线速度为v,d点的线速度为2v,根据向心加速度公式,可知a点与d点的向心加速度大小之比1:1,故D错误。
故选:ABC。
【点评】考查对圆周运动加速度、线速度与角速度的理解,属于基础知识,熟记公式。
(多选)7.(2024 江西模拟)陶瓷是中华瑰宝,是中华文明的重要名片。在陶瓷制作过程中有一道工序叫利坯,如图(a)所示,将陶瓷粗坯固定在绕竖直轴转动的水平转台上,用刀旋削,使坯体厚度适当,表里光洁。对应的简化模型如图(b)所示,粗坯的对称轴与转台转轴OO′重合。当转台转速恒定时,关于粗坯上P、Q两质点,下列说法正确的是( )
A.P的角速度大小比Q的大
B.P的线速度大小比Q的大
C.P的向心加速度大小比Q的大
D.同一时刻P所受合力的方向与Q的相同
【考点】向心加速度的表达式及影响向心加速度大小的因素;牛顿第二定律的简单应用;线速度的物理意义及计算;牛顿第二定律与向心力结合解决问题.
【专题】定性思想;方程法;匀速圆周运动专题;推理论证能力.
【答案】BC
【分析】同一圆环以直径为轴做匀速转动时,环上的点的角速度相同,根据几何关系可以判断Q、P两点各自做圆周运动的半径,根据v=ωr即可求解线速度,根据a=ω2r求得向心加速度。
【解答】解:A.由题意可知,粗坯上P、Q两质点属于同轴转动,它们的角速度相等,即ωP=ωQ,故A错误;
B.由图可知P点绕转轴转动的半径大,根据v=rω,所以vP>vQ,即P的线速度大小比Q的大,故B正确;
C.根据a=rω2,且rP>rQ,ωP=ωQ
所以aP>aQ
即P的向心加速度大小比Q的大,故C正确;
D.因为当转台转速恒定,所以同一时刻P所受合力的方向与Q的所受的合力方向均指向中心轴,故合力方向不相同,故D错误。
故选:BC。
【点评】该题主要考查了圆周运动基本公式的直接应用,注意同轴转动时角速度相同。
(多选)8.(2023秋 黔西南州期末)做匀速圆周运动的物体,10s内在沿半径为10m的圆周上运动了200m,则物体做匀速圆周运动时( )
A.周期为2πs
B.线速度的大小为20m/s
C.角速度的大小为2rad/s
D.向心加速度大小为20m/s2
【考点】向心加速度的计算;线速度与角速度的关系;角速度、周期、频率与转速的关系及计算.
【专题】定量思想;方程法;匀速圆周运动专题;推理论证能力.
【答案】BC
【分析】由题可知,物体做匀速圆周运动,根据匀速圆周运动的线速度、角速度、向心加速度的公式和周期与角速度的关系求解即可。
【解答】解:AB.线速度的大小m/s=20m/s
周期Ts=π(s),
故A错误,B正确;
C.角速度的大小rad/s=2rad/s,故C正确;
D.向心加速度大小为a=ω2R=22×10m/s2=40m/s2,故D错误。
故选:BC。
【点评】解题关键是能够根据题意求解线速度大小,掌握匀速圆周运动的角速度、向心加速度、周期的关系。
(多选)9.(2023秋 泰安期末)如图所示,自行车的小齿轮A、大齿轮B、后轮C的半径之比为1:3:9,在用力蹬脚踏板前进的过程中,下列说法正确的是( )
A.小齿轮A与后轮C的角速度大小之比为9:1
B.小齿轮A与大齿轮B的角速度大小之比为3:1
C.后轮C边缘与大齿轮B边缘各点的线速度大小之比为9:1
D.大齿轮B边缘与小齿轮A边缘各点的向心加速度大小之比为3:1
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度的物理意义及计算.
【专题】定量思想;比例法;匀速圆周运动专题;理解能力.
【答案】BC
【分析】在齿轮传动系统中,通过链条连接的齿轮边缘线速度相同,角速度与半径成反比,向心加速度与角速度的平方和半径成正比。
【解答】解:A、小齿轮和后轮是同轴转动,故小齿轮A与后轮C的角速度大小之比为1:1,故A错误;
B、小齿轮A与大齿轮B的线速度相等,根据题意,小齿轮A与大齿轮B的半径之比为1:3,根据公式v=ωr,小齿轮A与大齿轮B的角速度大小之比为3:1,故B正确。
C、小齿轮A与后轮C的角速度相同,根据公式v=ωr,故小齿轮A与后轮C的线速度之比为1:9,小齿轮A与大齿轮B的线速度相等,故后轮C边缘与大齿轮B边缘各点的线速度大小之比为9:1,故C正确;
D、小齿轮A与大齿轮B的线速度相等,根据公式可得,大齿轮B边缘与小齿轮A边缘各点的向心加速度大小之比为1:3,故D错误。
故选:BC。
【点评】本题考查的是齿轮传动中的角速度、线速度和向心加速度的关系。在自行车传动系统中,小齿轮A、大齿轮B和后轮C通过链条连接,因此在理想情况下,链条上各点的线速度相同。根据齿轮的半径比,可以推导出角速度和向心加速度的关系。
三.填空题(共3小题)
10.(2024秋 杨浦区校级期末)如图,两个齿轮相互咬合进行工作,C为大盘上的一点,A、B为大小两盘边缘上的两点,已知2rC=rA,rC=rB。工作时A点和B点的角速度之比ωA:ωB= 1:2 ,A点和C点向心加速度大小之比aA:aC= 2:1 。
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;传动问题.
【专题】定量思想;图析法;匀速圆周运动专题;理解能力.
【答案】1:2;2:1。
【分析】A、B两点都在齿轮边缘,相互咬合传动,故线速度大小相等,A点和C点角速度大小相等。
【解答】解:因为A、B两点都在齿轮边缘,相互咬合传动,故线速度大小相等,即vA:vB=1:1,根据公式v=ωr,可得,因为A、C在同一齿轮上,两点角速度相同,由a=rω2,可得aA:aC。
故答案为:1:2;2:1。
【点评】考查对圆周运动角速度、线速度、向心加速度的理解,熟悉公式的运用。
11.(2024秋 浦东新区校级期中)在地球表面赤道上的不同位置有两个物体m1、m2,如图所示.已知m1>m2,则m1、m2随地球自转的向心加速度的大小关系是a1 = a2(选填“<”“>”或“=”),所受向心力的大小关系是F1 > F2(选填“<”“>”或“=”)
【考点】向心加速度的表达式及影响向心加速度大小的因素.
【专题】定性思想;方程法;匀速圆周运动专题.
【答案】见试题解答内容
【分析】地球表面的物体都具有相等的角速度,由向心加速度和向心力的公式,比较二者的向心加速度与向心力的关系即可.
【解答】解:在地球表面赤道上的不同位置有两个物体具有相等的角速度和半径,设角速度为ω,半径为R,则向心加速度:a=ω2R,可知二者的向心加速度与质量无关,所以是相等的;向心力:,可知向心力的大小与物体的质量成正比,所以质量大的物体的向心力大,所以F1>F2.
故答案为:=,>
【点评】该题考查向心力与向心加速度的公式的应用,牢记向心力的公式和向心加速度的公式是解答的关键.
12.(2024春 普陀区校级期末)如图所示,做匀速圆周运动的质点在时间t内由A点运动到B点,AB弧所对的圆心角为θ。则质点的角速度大小为 ;若AB弧长为l,则质点向心加速度的大小为 。
【考点】向心加速度的计算;匀速圆周运动.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】,。
【分析】根据角速度的定义式、线速度定义式结合加速度的公式联立推导求解。
【解答】解:根据角速度的定义式,角速度的大小为ω,线速度大小为v,质点的向心加速度a=vω 。
故答案为:,。
【点评】考查角速度、线速度的定义式,会根据角速度和线速度的大小求解向心加速度大小。
四.解答题(共3小题)
13.(2024秋 包河区校级月考)匀速圆周运动和平抛是两种最典型的曲线运动。
(1)当物体做匀速圆周运动时,可以通过速度变化的情况来确定加速度的大小和方向。请用运动学的方法证明:一个物体做匀速圆周运动,其线速度大小为v,圆的半径为R(如图1所示)时,则其加速度大小为a。(已知角度θ很小时,有sinθ≈θ)
(2)研究一般曲线运动(如平抛)时,可以把这条曲线分割为很多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。质点所受合力F可以沿运动方向和垂直运动方向分解,沿切向的部分Ft使质点速度大小改变,垂直切向部分提供质点运动方向改变所需要的向心力Fn,满足:Fn≈m,其中v为质点在该点的瞬时速度,r为该点等效圆周运动半径(即曲率半径)。
一个可以看作质点的物块以初速度v0=3m/s离开桌面做平抛运动,桌面离地高度为h=0.8m,当地重力加速度为g=10m/s2。
a.物块运动的轨迹为抛物线,求该轨迹在抛出点P和落地点Q的曲率半径。
b.现制作一个与小物块平抛轨迹完全相同的光滑轨道,并将该轨道固定在与PQ曲线重合的位置,让物块从顶端P沿该轨道无初速下滑,试通过计算,分析说明小物块在落地前是否会脱离轨道。
【考点】向心加速度的计算;平抛运动与曲面的结合.
【专题】定量思想;推理法;平抛运动专题;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】(1)证明过程见上;
(2)a.该轨迹在抛出点P的曲率半径为0.9m,落地点Q的曲率半径为;
b.小物块在落地前不会脱离轨道。
【分析】(1)利用加速度公式以及三角形的相似关系进行推导;
(2)a.根据圆周运动和平抛的规律求该轨迹在抛出点P和落地点Q的曲率半径;
b.根据物体的运动情况分析轨道对物块是否有支持力作用,进而判断小物块在落地前是否会脱离轨道。
【解答】解:(1)若物体由图中的A点运动到B点,AB圆弧所对圆心角为θ,如图所示
可知三角形AOB与三角形DBC相似,则三角形DBC为等腰三角形,则
A点到B点的时间为
A点到B点的平均加速度为
解得
当圆心角O趋近于零(θ→0)时,则有
可得
(2)a.物块在抛出点P时,重力刚好与速度方向垂直,则有
解得该轨迹在抛出点P的曲率半径为
rp=0.9m
物块从抛出点P和落地点Q过程做平抛运动,则有
vy=gt
解得
vy=4m/s
则物块在落地点Q的速度大小为
解得
v=5m/s
物块在落地点Q的速度方向与水平方向的夹角满足
可得
θ=53°
则在落地点Q有
解得该轨迹在落地点Q的曲率半径为
b.物块做平抛运动过程经过某点的速度大小为v1,与水平方向的夹角为α,该点的曲率半径为r1,则有
现制作一个与小物块平抛轨迹完全相同的光滑轨道,并将该轨道固定在与PQ曲线重合的位置,让物块从顶端P沿该轨道无初速下滑,物块下滑到与平抛运动同一点时,重力做功相同,但平抛运动具有一定的初速度,所以物块无初速下滑时经过同一点的速度v′1小于物块做平抛运动经过同一点的速度v1,则有
可知轨道对物块有支持力作用,所以小物块在落地前不会脱离轨道。
答:(1)证明过程见上;
(2)a.该轨迹在抛出点P的曲率半径为0.9m,落地点Q的曲率半径为;
b.小物块在落地前不会脱离轨道。
【点评】本题的第一小题是是基本概念的再现,比较重视基础;在此基础上第二题又进行了灵活的变化,属于不同概念之间的迁移,比较灵活,非常考验学生的物理理解能力。难点在于极短时间内近似值的处理。
14.(2024春 天山区校级期末)如图所示,长度为L=10m的绳,系一小球在竖直面内做圆周运动,小球的质量为m=2kg,小球半径不计,小球在通过最低点时的速度大小为v=30m/s,试求:
(1)小球在最低点的向心加速度大小;
(2)小球在最低点所受绳的拉力大小。
【考点】向心加速度的计算;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;推理法;牛顿第二定律在圆周运动中的应用;推理论证能力.
【答案】(1)小球在最低点的向心加速度大小90m/s2;
(2)小球在最低点所受绳的拉力大200N。
【分析】(1)根据向心加速度公式,求向心加速度大小;
(2)根据牛顿第二定律,求拉力。
【解答】解:(1)小球在最低点的向心加速度大小
,代入数据得a=90m/s2
(2)根据牛顿第二定律
T﹣mg=ma
解得
T=200N
答:(1)小球在最低点的向心加速度大小90m/s2;
(2)小球在最低点所受绳的拉力大200N。
【点评】本题解题关键是掌握牛顿第二定律和向心加速度公式,比较基础。
15.(2024春 让胡路区校级期末)随着交通的发展,旅游才真正变成一件赏心乐事,各种“休闲游享乐游”纷纷打起了宣传的招牌,某次旅游中游客乘坐列车,以恒定速率通过一段水平圆弧形弯道过程中,发现车顶部悬挂玩具小熊的细线稳定后与车用侧壁平行。与车厢底板平行的桌面上有一水杯,已知水杯与桌面间的动摩擦因数μ,水杯与水的总质量m,水平圆弧形弯道半径R,此弯道路面的倾角为θ,重力加速度为g,不计空气阻力,求:
(1)列车转弯过程中的向心加速度大小;
(2)列车转弯过程中,水杯与桌面间的摩擦力。
【考点】向心加速度的计算;牛顿第二定律与向心力结合解决问题.
【专题】计算题;定量思想;合成分解法;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】(1)列车转弯过程中的向心加速度大小为gtanθ;
(2)列车转弯过程中,水杯与桌面间的摩擦力为0。
【分析】(1)对玩具小熊进行受力分析,结合牛顿第二定律求其向心加速度大小,即为列车转弯过程中的向心加速度大小;
(2)对水杯受力分析,其支持力和重力的合力提供向心力,未受到摩擦力。
【解答】解:(1)设玩具小熊的质量为m,则玩具小熊受到的重力mg、细线的拉力FT的合力提供玩具小熊随列车做圆周运动的向心力F,由牛顿第二定律有
mgtanθ=ma
可知列车在转弯过程中的向心加速度大小为a=gtanθ
(2)水杯的向心加速度a=gtanθ,则知水杯的向心力由水杯的重力与桌面的支持力的合力提供,则水杯与桌面间的静摩擦力为0。
答:(1)列车转弯过程中的向心加速度大小为gtanθ;
(2)列车转弯过程中,水杯与桌面间的摩擦力为0。
【点评】本题主要考查了圆周运动的相关应用,熟练对物体进行受力分析,结合牛顿第二定律和几何关系即可完成分析。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末押题预测 向心加速度
一.选择题(共5小题)
1.(2024秋 杨浦区校级期末)如图所示,同学们组成的跑操方阵排列整齐地匀速率通过圆弧形跑道区域,每个方阵中的每位同学均可视为做匀速圆周运动。则下列说法正确的是( )
A.每位同学的角速度相同
B.每位同学所受的合力为零
C.每位同学的速度大小相同
D.每位同学的加速度保持不变
2.(2024秋 道里区校级期末)如图所示、甲、乙两位同学握住绳子A、B两端摇动,A、B两端近似不动,且A、B两点连线沿水平方向,绳子上P、Q等各点均同步在竖直面做匀速圆周运动。当绳子在空中转到如图所示位置时,则( )
A.P点的线速度方向沿绳子切线
B.P点所受合外力垂直于绳斜向下
C.P点和Q点的线速度大小相等
D.P点的角速度等于Q点的角速度
3.(2024秋 朝阳区校级期末)如图所示,在长春市人民广场转盘,A、B两车正在水平圆形车道上做线速度大小相等的匀速圆周运动,下列说法正确的是( )
A.A车的角速度比B车的角速度小
B.A车的角速度比B车的角速度大
C.A车的向心加速度小于B车的向心加速度
D.A车的向心加速度等于B车的向心加速度
4.(2024秋 宁波期末)如图为修正带的内部结构,由大小两个相互咬合的齿轮组成,修正带芯固定在大齿轮的转轴上。当按压并拖动其头部时,齿轮转动,从而将遮盖物质均匀地涂抹在需要修改的字迹上。若图中大小齿轮的半径之比为2:1,A、B分别为大齿轮和小齿轮边缘上的一点,C为大齿轮上转轴半径的中点,则( )
A.A与B的角速度大小之比为1:2 B.B与C的线速度大小之比为1:1
C.A与C的向心加速度大小之比为4:1 D.大小齿轮的转动方向相同
5.(2024秋 龙岗区期末)脚踏车上的飞轮传动系统如图所示,设各轮的转轴均固定且相互平行,甲、乙两轮同轴且无相对转动,已知甲、乙、丙、丁四轮的半径比为5:2:3:1,A、B分别是甲、乙两轮边缘上的点,两传送带在四轮转动时均不打滑,下列判断正确的是( )
A.甲、乙两轮的角速度相等
B.A点向心加速度比B点的小
C.两传送带的线速度大小相等
D.当丙轮转1圈时,丁轮已转10圈
二.多选题(共4小题)
(多选)6.(2023秋 长沙校级期末)图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点。左侧是一轮轴,大轮的半径为4r,小轮的半径为2r。b点在小轮上,到小轮中心的距离为r。c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑。则( )
A.a点与b点的线速度大小之比为2:1
B.a点与b点的角速度大小之比2:1
C.a点与c点的线速度大小之比1:1
D.a点的向心加速度与d点的向心加速度之比2:1
(多选)7.(2024 江西模拟)陶瓷是中华瑰宝,是中华文明的重要名片。在陶瓷制作过程中有一道工序叫利坯,如图(a)所示,将陶瓷粗坯固定在绕竖直轴转动的水平转台上,用刀旋削,使坯体厚度适当,表里光洁。对应的简化模型如图(b)所示,粗坯的对称轴与转台转轴OO′重合。当转台转速恒定时,关于粗坯上P、Q两质点,下列说法正确的是( )
A.P的角速度大小比Q的大
B.P的线速度大小比Q的大
C.P的向心加速度大小比Q的大
D.同一时刻P所受合力的方向与Q的相同
(多选)8.(2023秋 黔西南州期末)做匀速圆周运动的物体,10s内在沿半径为10m的圆周上运动了200m,则物体做匀速圆周运动时( )
A.周期为2πs
B.线速度的大小为20m/s
C.角速度的大小为2rad/s
D.向心加速度大小为20m/s2
(多选)9.(2023秋 泰安期末)如图所示,自行车的小齿轮A、大齿轮B、后轮C的半径之比为1:3:9,在用力蹬脚踏板前进的过程中,下列说法正确的是( )
A.小齿轮A与后轮C的角速度大小之比为9:1
B.小齿轮A与大齿轮B的角速度大小之比为3:1
C.后轮C边缘与大齿轮B边缘各点的线速度大小之比为9:1
D.大齿轮B边缘与小齿轮A边缘各点的向心加速度大小之比为3:1
三.填空题(共3小题)
10.(2024秋 杨浦区校级期末)如图,两个齿轮相互咬合进行工作,C为大盘上的一点,A、B为大小两盘边缘上的两点,已知2rC=rA,rC=rB。工作时A点和B点的角速度之比ωA:ωB= ,A点和C点向心加速度大小之比aA:aC= 。
11.(2024秋 浦东新区校级期中)在地球表面赤道上的不同位置有两个物体m1、m2,如图所示.已知m1>m2,则m1、m2随地球自转的向心加速度的大小关系是a1 a2(选填“<”“>”或“=”),所受向心力的大小关系是F1 F2(选填“<”“>”或“=”)
12.(2024春 普陀区校级期末)如图所示,做匀速圆周运动的质点在时间t内由A点运动到B点,AB弧所对的圆心角为θ。则质点的角速度大小为 ;若AB弧长为l,则质点向心加速度的大小为 。
四.解答题(共3小题)
13.(2024秋 包河区校级月考)匀速圆周运动和平抛是两种最典型的曲线运动。
(1)当物体做匀速圆周运动时,可以通过速度变化的情况来确定加速度的大小和方向。请用运动学的方法证明:一个物体做匀速圆周运动,其线速度大小为v,圆的半径为R(如图1所示)时,则其加速度大小为a。(已知角度θ很小时,有sinθ≈θ)
(2)研究一般曲线运动(如平抛)时,可以把这条曲线分割为很多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。质点所受合力F可以沿运动方向和垂直运动方向分解,沿切向的部分Ft使质点速度大小改变,垂直切向部分提供质点运动方向改变所需要的向心力Fn,满足:Fn≈m,其中v为质点在该点的瞬时速度,r为该点等效圆周运动半径(即曲率半径)。
一个可以看作质点的物块以初速度v0=3m/s离开桌面做平抛运动,桌面离地高度为h=0.8m,当地重力加速度为g=10m/s2。
a.物块运动的轨迹为抛物线,求该轨迹在抛出点P和落地点Q的曲率半径。
b.现制作一个与小物块平抛轨迹完全相同的光滑轨道,并将该轨道固定在与PQ曲线重合的位置,让物块从顶端P沿该轨道无初速下滑,试通过计算,分析说明小物块在落地前是否会脱离轨道。
14.(2024春 天山区校级期末)如图所示,长度为L=10m的绳,系一小球在竖直面内做圆周运动,小球的质量为m=2kg,小球半径不计,小球在通过最低点时的速度大小为v=30m/s,试求:
(1)小球在最低点的向心加速度大小;
(2)小球在最低点所受绳的拉力大小。
15.(2024春 让胡路区校级期末)随着交通的发展,旅游才真正变成一件赏心乐事,各种“休闲游享乐游”纷纷打起了宣传的招牌,某次旅游中游客乘坐列车,以恒定速率通过一段水平圆弧形弯道过程中,发现车顶部悬挂玩具小熊的细线稳定后与车用侧壁平行。与车厢底板平行的桌面上有一水杯,已知水杯与桌面间的动摩擦因数μ,水杯与水的总质量m,水平圆弧形弯道半径R,此弯道路面的倾角为θ,重力加速度为g,不计空气阻力,求:
(1)列车转弯过程中的向心加速度大小;
(2)列车转弯过程中,水杯与桌面间的摩擦力。
期末押题预测 向心加速度
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 杨浦区校级期末)如图所示,同学们组成的跑操方阵排列整齐地匀速率通过圆弧形跑道区域,每个方阵中的每位同学均可视为做匀速圆周运动。则下列说法正确的是( )
A.每位同学的角速度相同
B.每位同学所受的合力为零
C.每位同学的速度大小相同
D.每位同学的加速度保持不变
【考点】向心加速度的概念、方向及物理意义;匀速圆周运动;线速度与角速度的关系.
【专题】定性思想;推理法;匀速圆周运动专题;理解能力.
【答案】A
【分析】根据匀速圆周运动的特点:绕同一圆心做圆周运动其角速度相同,线速度v=ωr判定线速度,合外力提供向心力,加速度始终指向圆心。
【解答】解:A.每个方阵中的每位同学均可视为绕同一圆心做匀速圆周运动,则角速度相同。故A正确;
B.每位同学均做匀速圆周运动,所受的合力提供向心力,合力不为零。故B错误;
C.根据v=ωr可知每位同学的运动半径不同,其速度大小不相同。故C错误;
D.根据a=ω2r可知每位同学的加速度大小保持不变,方向指向圆心,时刻改变。故D错误。
故选:A。
【点评】本题主要考查了匀速圆周运动的特点,解题关键是掌握绕同一圆心做圆周运动其角速度相同,线速度v=ωr判定线速度,合外力提供向心力,加速度始终指向圆心。
2.(2024秋 道里区校级期末)如图所示、甲、乙两位同学握住绳子A、B两端摇动,A、B两端近似不动,且A、B两点连线沿水平方向,绳子上P、Q等各点均同步在竖直面做匀速圆周运动。当绳子在空中转到如图所示位置时,则( )
A.P点的线速度方向沿绳子切线
B.P点所受合外力垂直于绳斜向下
C.P点和Q点的线速度大小相等
D.P点的角速度等于Q点的角速度
【考点】向心加速度的计算;线速度与角速度的关系.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】D
【分析】AB.根据题意分析P点的圆周平面,判断P点的合外力方向和速度方向;
CD.根据共轴转动情况判断角速度关系,结合半径差异判断线速度大小关系。
【解答】解:AB.P点做匀速圆周运动的圆心是过P点作图中虚线的垂线和虚线的交点,故P点所受合力方向指向交点,方向竖直向下,P点线速度方向为垂直于纸面向里或向外,故AB错误;
CD.由于是共轴转动,故P点的角速度等于Q点的角速度,P点圆周运动半径小于Q点,则P点线速度大小小于Q点的线速度大小,故C错误,D正确。
故选:D。
【点评】考查圆周运动的合外力和线速度规律,结合共轴转动问题判断线速度大小关系。
3.(2024秋 朝阳区校级期末)如图所示,在长春市人民广场转盘,A、B两车正在水平圆形车道上做线速度大小相等的匀速圆周运动,下列说法正确的是( )
A.A车的角速度比B车的角速度小
B.A车的角速度比B车的角速度大
C.A车的向心加速度小于B车的向心加速度
D.A车的向心加速度等于B车的向心加速度
【考点】向心加速度的计算;线速度与角速度的关系.
【专题】比较思想;归纳法;匀速圆周运动专题;理解能力.
【答案】B
【分析】根据分析角速度的大小;根据a分析向心加速度的大小。
【解答】解:AB、由图知A的半径小于B的半径,根据可知,A的角速度大于B的角速度,故A错误,B正确;
CD、根据a可知,A车的向心加速度大于B车的向心加速度,故CD错误。
故选:B。
【点评】本题考查了角速度和线速度的关系,以及向心加速度和线速度的关系式,容易题。
4.(2024秋 宁波期末)如图为修正带的内部结构,由大小两个相互咬合的齿轮组成,修正带芯固定在大齿轮的转轴上。当按压并拖动其头部时,齿轮转动,从而将遮盖物质均匀地涂抹在需要修改的字迹上。若图中大小齿轮的半径之比为2:1,A、B分别为大齿轮和小齿轮边缘上的一点,C为大齿轮上转轴半径的中点,则( )
A.A与B的角速度大小之比为1:2
B.B与C的线速度大小之比为1:1
C.A与C的向心加速度大小之比为4:1
D.大小齿轮的转动方向相同
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;角速度、周期、频率与转速的关系及计算;传动问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】A
【分析】同缘传动时,边缘点的线速度相等;同轴传动时,角速度相等;然后结合v=ωr列式求解。
【解答】解:ABC.边缘点的线速度大小相等,故vA:vB=1:1,同轴传动时,角速度相等,故ωA=ωC,角速度大小之比为1:1,根据v=ωr,结合半径的比值关系:rA:rB:rC=2:1:1。可知,ωA:ωB:ωC=1:2:1,vA:vB:vC=2:2:1;向心加速度的表达式可得:a=ω2r解得:aA:aB:aC=2:4:1,故A正确,BC错误;
D、大、小齿轮相互咬合,同缘传动时,大、小齿轮转动方向相反,故D错误;
故选:A。
【点评】本题关键明确同缘传动同轴传动的特点:同轴传动时,角速度相等,同缘传动时,边缘点的线速度相等,然后结合公式v=ωr分析求解即可。
5.(2024秋 龙岗区期末)脚踏车上的飞轮传动系统如图所示,设各轮的转轴均固定且相互平行,甲、乙两轮同轴且无相对转动,已知甲、乙、丙、丁四轮的半径比为5:2:3:1,A、B分别是甲、乙两轮边缘上的点,两传送带在四轮转动时均不打滑,下列判断正确的是( )
A.甲、乙两轮的角速度相等
B.A点向心加速度比B点的小
C.两传送带的线速度大小相等
D.当丙轮转1圈时,丁轮已转10圈
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;传动问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】A
【分析】各轮转轴固定且平行,甲、乙两轮同轴无相对转动,意味着甲、乙两轮角速度相等,甲、乙、丙、丁四轮半径之比为5:2:3:1,且传送带不打滑,说明与轮子接触处传送带线速度和轮子边缘线速度相等,据此分析解答即可。
【解答】解:A.因为甲、乙两轮同轴无相对转动,根据同轴转动的物体角速度相等这一特性,所以甲、乙两轮的角速度相等,故A正确。
B.根据向心加速度公式a = ω2r,甲、乙两轮角速度ω相等,A点在甲轮边缘,B点在乙轮边缘,甲轮半径大于乙轮半径,所以A点向心加速度比B点的大,故B错误。
CD.设甲轮半径r甲=5r,乙轮半径r乙=2r,丙轮半径r丙=3r,丁轮半径r丁=r,由于甲、乙两轮角速度相等,设为ω,则甲轮边缘线速度为
v甲=ωr甲
解得:v甲=5rω,
乙轮边缘线速度为
v乙=ωr乙
解得:v乙=2rω
根据同一传动装置接触边缘的线速度大小是相等及v= ωr得:
ω丙
联立解得:
所以丙轮转1圈时,丁轮转了圈,两传送带线速度大小不相等,故CD错误。
故选:A。
【点评】本题考查了线速度与角速度关系,知道共轴的角速度是相同的,同一传动装置接触边缘的线速度大小是相等的,注意灵活应用线速度、角速度与半径之间的关系.
二.多选题(共4小题)
(多选)6.(2023秋 长沙校级期末)图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点。左侧是一轮轴,大轮的半径为4r,小轮的半径为2r。b点在小轮上,到小轮中心的距离为r。c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑。则( )
A.a点与b点的线速度大小之比为2:1
B.a点与b点的角速度大小之比2:1
C.a点与c点的线速度大小之比1:1
D.a点的向心加速度与d点的向心加速度之比2:1
【考点】向心加速度的表达式及影响向心加速度大小的因素;传动问题.
【专题】定量思想;比例法;匀速圆周运动专题;理解能力.
【答案】ABC
【分析】右轮与左侧小轮的线速度相等,左侧大轮与小轮的角速度相等,根据圆周运动公式分析。
【解答】解:C.如图所示,a与c同一皮带下传动,则线速度va=vc,故C正确;
AB.根据v=ωr,可得ωa:ωc=rc:ra=2:1,因为ωb=ωc=ωd,且rb:rc=1:2,所以vb:vc=1:2,则va:vb=2:1,ωa:ωb=2:1,故AB正确;
D.设a点的线速度为v,由以上分析可知,c点的线速度为v,d点的线速度为2v,根据向心加速度公式,可知a点与d点的向心加速度大小之比1:1,故D错误。
故选:ABC。
【点评】考查对圆周运动加速度、线速度与角速度的理解,属于基础知识,熟记公式。
(多选)7.(2024 江西模拟)陶瓷是中华瑰宝,是中华文明的重要名片。在陶瓷制作过程中有一道工序叫利坯,如图(a)所示,将陶瓷粗坯固定在绕竖直轴转动的水平转台上,用刀旋削,使坯体厚度适当,表里光洁。对应的简化模型如图(b)所示,粗坯的对称轴与转台转轴OO′重合。当转台转速恒定时,关于粗坯上P、Q两质点,下列说法正确的是( )
A.P的角速度大小比Q的大
B.P的线速度大小比Q的大
C.P的向心加速度大小比Q的大
D.同一时刻P所受合力的方向与Q的相同
【考点】向心加速度的表达式及影响向心加速度大小的因素;牛顿第二定律的简单应用;线速度的物理意义及计算;牛顿第二定律与向心力结合解决问题.
【专题】定性思想;方程法;匀速圆周运动专题;推理论证能力.
【答案】BC
【分析】同一圆环以直径为轴做匀速转动时,环上的点的角速度相同,根据几何关系可以判断Q、P两点各自做圆周运动的半径,根据v=ωr即可求解线速度,根据a=ω2r求得向心加速度。
【解答】解:A.由题意可知,粗坯上P、Q两质点属于同轴转动,它们的角速度相等,即ωP=ωQ,故A错误;
B.由图可知P点绕转轴转动的半径大,根据v=rω,所以vP>vQ,即P的线速度大小比Q的大,故B正确;
C.根据a=rω2,且rP>rQ,ωP=ωQ
所以aP>aQ
即P的向心加速度大小比Q的大,故C正确;
D.因为当转台转速恒定,所以同一时刻P所受合力的方向与Q的所受的合力方向均指向中心轴,故合力方向不相同,故D错误。
故选:BC。
【点评】该题主要考查了圆周运动基本公式的直接应用,注意同轴转动时角速度相同。
(多选)8.(2023秋 黔西南州期末)做匀速圆周运动的物体,10s内在沿半径为10m的圆周上运动了200m,则物体做匀速圆周运动时( )
A.周期为2πs
B.线速度的大小为20m/s
C.角速度的大小为2rad/s
D.向心加速度大小为20m/s2
【考点】向心加速度的计算;线速度与角速度的关系;角速度、周期、频率与转速的关系及计算.
【专题】定量思想;方程法;匀速圆周运动专题;推理论证能力.
【答案】BC
【分析】由题可知,物体做匀速圆周运动,根据匀速圆周运动的线速度、角速度、向心加速度的公式和周期与角速度的关系求解即可。
【解答】解:AB.线速度的大小m/s=20m/s
周期Ts=π(s),
故A错误,B正确;
C.角速度的大小rad/s=2rad/s,故C正确;
D.向心加速度大小为a=ω2R=22×10m/s2=40m/s2,故D错误。
故选:BC。
【点评】解题关键是能够根据题意求解线速度大小,掌握匀速圆周运动的角速度、向心加速度、周期的关系。
(多选)9.(2023秋 泰安期末)如图所示,自行车的小齿轮A、大齿轮B、后轮C的半径之比为1:3:9,在用力蹬脚踏板前进的过程中,下列说法正确的是( )
A.小齿轮A与后轮C的角速度大小之比为9:1
B.小齿轮A与大齿轮B的角速度大小之比为3:1
C.后轮C边缘与大齿轮B边缘各点的线速度大小之比为9:1
D.大齿轮B边缘与小齿轮A边缘各点的向心加速度大小之比为3:1
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度的物理意义及计算.
【专题】定量思想;比例法;匀速圆周运动专题;理解能力.
【答案】BC
【分析】在齿轮传动系统中,通过链条连接的齿轮边缘线速度相同,角速度与半径成反比,向心加速度与角速度的平方和半径成正比。
【解答】解:A、小齿轮和后轮是同轴转动,故小齿轮A与后轮C的角速度大小之比为1:1,故A错误;
B、小齿轮A与大齿轮B的线速度相等,根据题意,小齿轮A与大齿轮B的半径之比为1:3,根据公式v=ωr,小齿轮A与大齿轮B的角速度大小之比为3:1,故B正确。
C、小齿轮A与后轮C的角速度相同,根据公式v=ωr,故小齿轮A与后轮C的线速度之比为1:9,小齿轮A与大齿轮B的线速度相等,故后轮C边缘与大齿轮B边缘各点的线速度大小之比为9:1,故C正确;
D、小齿轮A与大齿轮B的线速度相等,根据公式可得,大齿轮B边缘与小齿轮A边缘各点的向心加速度大小之比为1:3,故D错误。
故选:BC。
【点评】本题考查的是齿轮传动中的角速度、线速度和向心加速度的关系。在自行车传动系统中,小齿轮A、大齿轮B和后轮C通过链条连接,因此在理想情况下,链条上各点的线速度相同。根据齿轮的半径比,可以推导出角速度和向心加速度的关系。
三.填空题(共3小题)
10.(2024秋 杨浦区校级期末)如图,两个齿轮相互咬合进行工作,C为大盘上的一点,A、B为大小两盘边缘上的两点,已知2rC=rA,rC=rB。工作时A点和B点的角速度之比ωA:ωB= 1:2 ,A点和C点向心加速度大小之比aA:aC= 2:1 。
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;传动问题.
【专题】定量思想;图析法;匀速圆周运动专题;理解能力.
【答案】1:2;2:1。
【分析】A、B两点都在齿轮边缘,相互咬合传动,故线速度大小相等,A点和C点角速度大小相等。
【解答】解:因为A、B两点都在齿轮边缘,相互咬合传动,故线速度大小相等,即vA:vB=1:1,根据公式v=ωr,可得,因为A、C在同一齿轮上,两点角速度相同,由a=rω2,可得aA:aC。
故答案为:1:2;2:1。
【点评】考查对圆周运动角速度、线速度、向心加速度的理解,熟悉公式的运用。
11.(2024秋 浦东新区校级期中)在地球表面赤道上的不同位置有两个物体m1、m2,如图所示.已知m1>m2,则m1、m2随地球自转的向心加速度的大小关系是a1 = a2(选填“<”“>”或“=”),所受向心力的大小关系是F1 > F2(选填“<”“>”或“=”)
【考点】向心加速度的表达式及影响向心加速度大小的因素.
【专题】定性思想;方程法;匀速圆周运动专题.
【答案】见试题解答内容
【分析】地球表面的物体都具有相等的角速度,由向心加速度和向心力的公式,比较二者的向心加速度与向心力的关系即可.
【解答】解:在地球表面赤道上的不同位置有两个物体具有相等的角速度和半径,设角速度为ω,半径为R,则向心加速度:a=ω2R,可知二者的向心加速度与质量无关,所以是相等的;向心力:,可知向心力的大小与物体的质量成正比,所以质量大的物体的向心力大,所以F1>F2.
故答案为:=,>
【点评】该题考查向心力与向心加速度的公式的应用,牢记向心力的公式和向心加速度的公式是解答的关键.
12.(2024春 普陀区校级期末)如图所示,做匀速圆周运动的质点在时间t内由A点运动到B点,AB弧所对的圆心角为θ。则质点的角速度大小为 ;若AB弧长为l,则质点向心加速度的大小为 。
【考点】向心加速度的计算;匀速圆周运动.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】,。
【分析】根据角速度的定义式、线速度定义式结合加速度的公式联立推导求解。
【解答】解:根据角速度的定义式,角速度的大小为ω,线速度大小为v,质点的向心加速度a=vω 。
故答案为:,。
【点评】考查角速度、线速度的定义式,会根据角速度和线速度的大小求解向心加速度大小。
四.解答题(共3小题)
13.(2024秋 包河区校级月考)匀速圆周运动和平抛是两种最典型的曲线运动。
(1)当物体做匀速圆周运动时,可以通过速度变化的情况来确定加速度的大小和方向。请用运动学的方法证明:一个物体做匀速圆周运动,其线速度大小为v,圆的半径为R(如图1所示)时,则其加速度大小为a。(已知角度θ很小时,有sinθ≈θ)
(2)研究一般曲线运动(如平抛)时,可以把这条曲线分割为很多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。质点所受合力F可以沿运动方向和垂直运动方向分解,沿切向的部分Ft使质点速度大小改变,垂直切向部分提供质点运动方向改变所需要的向心力Fn,满足:Fn≈m,其中v为质点在该点的瞬时速度,r为该点等效圆周运动半径(即曲率半径)。
一个可以看作质点的物块以初速度v0=3m/s离开桌面做平抛运动,桌面离地高度为h=0.8m,当地重力加速度为g=10m/s2。
a.物块运动的轨迹为抛物线,求该轨迹在抛出点P和落地点Q的曲率半径。
b.现制作一个与小物块平抛轨迹完全相同的光滑轨道,并将该轨道固定在与PQ曲线重合的位置,让物块从顶端P沿该轨道无初速下滑,试通过计算,分析说明小物块在落地前是否会脱离轨道。
【考点】向心加速度的计算;平抛运动与曲面的结合.
【专题】定量思想;推理法;平抛运动专题;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】(1)证明过程见上;
(2)a.该轨迹在抛出点P的曲率半径为0.9m,落地点Q的曲率半径为;
b.小物块在落地前不会脱离轨道。
【分析】(1)利用加速度公式以及三角形的相似关系进行推导;
(2)a.根据圆周运动和平抛的规律求该轨迹在抛出点P和落地点Q的曲率半径;
b.根据物体的运动情况分析轨道对物块是否有支持力作用,进而判断小物块在落地前是否会脱离轨道。
【解答】解:(1)若物体由图中的A点运动到B点,AB圆弧所对圆心角为θ,如图所示
可知三角形AOB与三角形DBC相似,则三角形DBC为等腰三角形,则
A点到B点的时间为
A点到B点的平均加速度为
解得
当圆心角O趋近于零(θ→0)时,则有
可得
(2)a.物块在抛出点P时,重力刚好与速度方向垂直,则有
解得该轨迹在抛出点P的曲率半径为
rp=0.9m
物块从抛出点P和落地点Q过程做平抛运动,则有
vy=gt
解得
vy=4m/s
则物块在落地点Q的速度大小为
解得
v=5m/s
物块在落地点Q的速度方向与水平方向的夹角满足
可得
θ=53°
则在落地点Q有
解得该轨迹在落地点Q的曲率半径为
b.物块做平抛运动过程经过某点的速度大小为v1,与水平方向的夹角为α,该点的曲率半径为r1,则有
现制作一个与小物块平抛轨迹完全相同的光滑轨道,并将该轨道固定在与PQ曲线重合的位置,让物块从顶端P沿该轨道无初速下滑,物块下滑到与平抛运动同一点时,重力做功相同,但平抛运动具有一定的初速度,所以物块无初速下滑时经过同一点的速度v′1小于物块做平抛运动经过同一点的速度v1,则有
可知轨道对物块有支持力作用,所以小物块在落地前不会脱离轨道。
答:(1)证明过程见上;
(2)a.该轨迹在抛出点P的曲率半径为0.9m,落地点Q的曲率半径为;
b.小物块在落地前不会脱离轨道。
【点评】本题的第一小题是是基本概念的再现,比较重视基础;在此基础上第二题又进行了灵活的变化,属于不同概念之间的迁移,比较灵活,非常考验学生的物理理解能力。难点在于极短时间内近似值的处理。
14.(2024春 天山区校级期末)如图所示,长度为L=10m的绳,系一小球在竖直面内做圆周运动,小球的质量为m=2kg,小球半径不计,小球在通过最低点时的速度大小为v=30m/s,试求:
(1)小球在最低点的向心加速度大小;
(2)小球在最低点所受绳的拉力大小。
【考点】向心加速度的计算;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;推理法;牛顿第二定律在圆周运动中的应用;推理论证能力.
【答案】(1)小球在最低点的向心加速度大小90m/s2;
(2)小球在最低点所受绳的拉力大200N。
【分析】(1)根据向心加速度公式,求向心加速度大小;
(2)根据牛顿第二定律,求拉力。
【解答】解:(1)小球在最低点的向心加速度大小
,代入数据得a=90m/s2
(2)根据牛顿第二定律
T﹣mg=ma
解得
T=200N
答:(1)小球在最低点的向心加速度大小90m/s2;
(2)小球在最低点所受绳的拉力大200N。
【点评】本题解题关键是掌握牛顿第二定律和向心加速度公式,比较基础。
15.(2024春 让胡路区校级期末)随着交通的发展,旅游才真正变成一件赏心乐事,各种“休闲游享乐游”纷纷打起了宣传的招牌,某次旅游中游客乘坐列车,以恒定速率通过一段水平圆弧形弯道过程中,发现车顶部悬挂玩具小熊的细线稳定后与车用侧壁平行。与车厢底板平行的桌面上有一水杯,已知水杯与桌面间的动摩擦因数μ,水杯与水的总质量m,水平圆弧形弯道半径R,此弯道路面的倾角为θ,重力加速度为g,不计空气阻力,求:
(1)列车转弯过程中的向心加速度大小;
(2)列车转弯过程中,水杯与桌面间的摩擦力。
【考点】向心加速度的计算;牛顿第二定律与向心力结合解决问题.
【专题】计算题;定量思想;合成分解法;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】(1)列车转弯过程中的向心加速度大小为gtanθ;
(2)列车转弯过程中,水杯与桌面间的摩擦力为0。
【分析】(1)对玩具小熊进行受力分析,结合牛顿第二定律求其向心加速度大小,即为列车转弯过程中的向心加速度大小;
(2)对水杯受力分析,其支持力和重力的合力提供向心力,未受到摩擦力。
【解答】解:(1)设玩具小熊的质量为m,则玩具小熊受到的重力mg、细线的拉力FT的合力提供玩具小熊随列车做圆周运动的向心力F,由牛顿第二定律有
mgtanθ=ma
可知列车在转弯过程中的向心加速度大小为a=gtanθ
(2)水杯的向心加速度a=gtanθ,则知水杯的向心力由水杯的重力与桌面的支持力的合力提供,则水杯与桌面间的静摩擦力为0。
答:(1)列车转弯过程中的向心加速度大小为gtanθ;
(2)列车转弯过程中,水杯与桌面间的摩擦力为0。
【点评】本题主要考查了圆周运动的相关应用,熟练对物体进行受力分析,结合牛顿第二定律和几何关系即可完成分析。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
