周测 19.2 一次函数 (19.2.1~19.2.2第 3课时--等4课时) (含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 周测 19.2 一次函数 (19.2.1~19.2.2第 3课时--等4课时) (含答案)2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 185.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览




文档简介
周测(19.2.1~19.2.2第 3课时)
(时间:40 分钟 满分:100分)
一、选择题(每小题4分,共24分)
1.下列函数中,不是一次函数的是 ( )
A. y=-x+4
2.已知正比例函数y=kx的图象经过点( ),则k= ( )
A. B. C. D.5
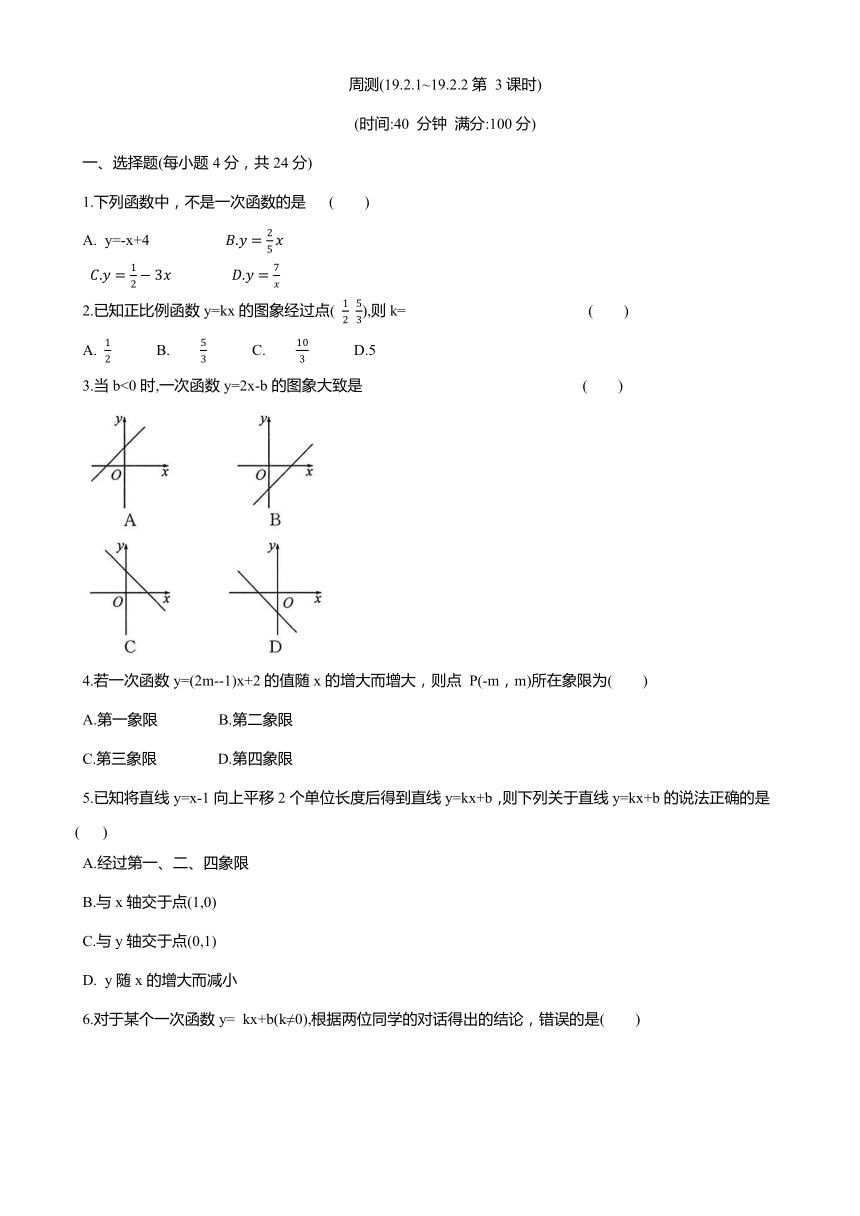
3.当b<0时,一次函数y=2x-b的图象大致是 ( )
4.若一次函数y=(2m--1)x+2的值随x的增大而增大,则点 P(-m,m)所在象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知将直线y=x-1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是 ( )
A.经过第一、二、四象限
B.与x轴交于点(1,0)
C.与y轴交于点(0,1)
D. y随x的增大而减小
6.对于某个一次函数y= kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A. k>0 B. kb<0
C. k+b>0
二、填空题(每小题5分,共30分)
7.已知一次函数y=-x+2的图象经过点A(n,3),则n的值是 .
8.若函数 是关于 x 的正比例函数,则m+n= .
9.甲、乙两名同学观察完某个一次函数的图象后,分别得到下列结论:
甲:函数的图象经过点(0,1).
乙:y随x的增大而减小.
根据他们的叙述,写出满足上述结论的一个函数解析式: .
10.已知点 A(m,2),B(n,-3)在一次函数y= 的图象上,则m,n的大小关系是 m n(填“>”“<”或“=”).
11.如图,点 B 的坐标是(0,3),将△OAB沿x轴向右平移得到△CDE,点 B 的对应点 E 恰好落在直线y=2x--3上,则点A移动的距离是 .
12.已知 P 是直线y=-2x+4上的一个动点,若点 P 到两坐标轴的距离相等,则点P 的坐标是 .
三、解答题(共46分)
13.(8分)已知关于x的一次函数y=(1-2m)x+m+1的图象经过第一、二、三象限,求m的取值范围.
14.(10 分)在平面直角坐标系内有三点 A(--1,4),B(--3,2),C(0,6).
(1)求过其中两点的直线的函数解析式(选一种情形作答).
(2)判断A,B,C三点是否在同一条直线上,并说明理由.
15.(13分)如图,已知直线 与x轴、y轴分别交于点A,B,直线 与直线y= ax+b(a,b为常数,且a≠0)关于x轴对称,直线 y=ax+b与y 轴交于点C.
(1)求a,b的值.
(2)P 是直线AC 在x 轴上方的一个动点,当△ABP 的面积为 6 时,求点 P的坐标.
16.(15分)如图,直线 与x轴,y轴分别交于点 A(-3,0),B(0,3),直线 l : 与直线 l 相交于点
(1)求直线 l 和 l 的解析式.
(2)M为 y轴上一动点,连接 MA,MC,当 的值最小时,求点 M的坐标.
周测(19.2.2第4课时~19.3)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共24分)
1. 直线 y= ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程 ax+b=0的解为 ( )
A. x=0 B. x=1 C. x=2 D. x=3
2.如图,直线 y= ax+b(a≠0)过点 A,B,则不等式 ax+b>0的解集是 ( )
B. x>-3
C. x>0 D. x>4
3.如图,一次函数y=2x和y= ax+4的图象相交于点 A(m,3),则关于x,y的方程组 的解为 ( )
A.10° D.{x=2,
4.已知一次函数y=kx+b的图象如图所示,当x<1时,y的取值范围是 ( )
A.0C. y>0
5.生物活动小组的同学们观察某植物生长,得到该植物的高度 y(cm)与观察时间x(天)的关系,并画出如图所示的图象(CD∥x轴),该植物的最高高度是 ( )
A. 50cm B. 20cm C.16 cm D.26 cm
6.某商场销售一种儿童滑板车,经市场调查,售价x(元)、每星期销量y(件)、单件利润w(元)之间的关系如图 1、图2 所示.若某星期该滑板车的单件利润为20元,则本星期该滑板车的销量为 ( )
A.94件 B.96件
C.1600件 D.1800件
二、填空题(每小题4分,共20分)
7.已知方程2x+1=-x+4的解是x=1,则在同一平面直角坐标系中直线 y=2x+1与y=--x+4的交点坐标是 .
8.如图,直线 y= kx+b(k,b是常数,k≠0)与直线 y=2 交于点 A(4,2),则关于x的不等式 kx+b<2的解集为 .
9.某公司急需用车,但又不准备买车,公司准备和一个个体车主或一家出租车公司签订月租车合同,他们的月收费y(元)与公司每月用车的路程x(千米)之间的关系如图所示(其中个体车主收费为 y 元,出租车公司收费为y 元),则当x 时,选用个体车主较划算.
10.我们规定:当k,b为常数(k≠0,b≠0,k≠b)时,一次函数y= kx+b与y= bx+k互为“交换函数”,例如y=4x+3的“交换函数”为 y=3x+4.则一次函数 y= kx+2与它的“交换函数”图象的交点横坐标为
11.一次函数y=-2x+4与y=x---2的图象与 y轴所围成的三角形的面积为 .
三、解答题(共56分)
12.(12分)已知一次函数y=--2x+4,解决下列问题:
(1)在所给平面直角坐标系中画出此函数的图象.
(2)根据图象回答:当x= 时,-2x+4=4.
(3)根据图象回答:当x 时,y>0.
13.(13分)如图,在平面直角坐标系中,一次函数 y=kx+b的图象与 x轴的交点为A(-3,0),与 y轴的交点为 B,且与正比例函数 的图象交于点C(m,4).
(1)求一次函数y= kx+b的解析式.
(2)关于x的不等式 的解集为 .
14.(14分)如图,在平面直角坐标系中,一次函数y=kx+9的图象与 y轴相交于点A,与x轴相交于点C,并与直线 相交于点B,其中点 B 的横坐标为3.
(1)求点 B 的坐标和k 的值.
(2)Q为直线y= kx+9上一动点,当点 Q运动到何位置时,△OBQ的面积等于 请求出点Q的坐标.
15.(17分)甲、乙两车沿相同的路线由 A 地到 B 地匀速前进,A,B两地间的路程为200km,甲、乙两车前进的路程分别为s (km),s (km),甲车出发后的时间为t(h),甲、乙两车前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:
(1)甲车的速度是 km/h,乙车比甲车晚出发 h.
(2)请分别求出甲、乙两车前进的路程s ,s 与甲车出发后的时间t之间的函数关系式.
(3)甲车经过多长时间被乙车追上 此时两车距离 B地还有多远
周测(19.2.1~19.2.2 第 3课时)
1. D 2. C 3. A 4. B 5. C 6. C 7.-1 8.2 9. y=-x+1(答案不唯一) 10.< 11.3 1 2.( , )或(4,-4)
13.解:∵一次函数y=(1-2m)x+m+1的图象经过第一、二、三象限 解得 ∴m的取值范围是-1<
14.解:(1)设过A(-1,4),B(-3,2)两点的直线AB的解析式为y=kx+b,则 解得 直线 AB 的解析式为y=x+5.(答案不唯一)(2)A,B,C三点不在同一条直线上.理由:当x=0时,y=0+5≠6,∴点C(0,6)不在直线AB上,即点A,B,C三点不在同一直线上.
15.解:(1)在 中,令x=0,则.y=-2.∴B(0,-2).令y=0,则 解得x=4.∴A(4,0).∵直线 与直线y= ax+b关于x轴对称,∴直线y= ax+b过点A(4,0)和点C(0,2).把点 A(4,0),C(0,2)代入 y= ax+b,得 解得 由(1)得,直线.y= ax+b的解析式为 2.设点 P 的横坐标为m,则 解得m=1.∴点 P的坐标为((1, ).
16.解:(1)把A(-3,0),B(0,3)代入 得 解得直线l 的解析式为y=x+3.把 代入y=x+3,得 把 代入 得 解得k =-3.∴直线l 的解析式为 y=-3x.(2)作点 A 关于y轴的对称点A',连接A'C,交 y轴于点M',连接AM',∵点A关于y轴的对称点为点A',∴MA=A'M.∴若MA+MC的值最小,则A'M+MC的值最小.当A',M,C三点共线时,MA+MC的值最小.∵A(-3,0),点 A 关于y轴的对称点为点A',∴A'(3,0).设直线A'C的解析式为y= mx+t,把A'(3,0),C(- , )代入y= mx+t,得 解得 直线 A'C的解析式为 令x=0,得 点M的坐标为(0, ).
周测(19.2.2第4课时~19.3)
1. C 2. B 3. A 4. D 5. C 6. D 7.(1,3) 8. x<4 9.>180010.1 11.6
12.解:(1)图略.(2)0 (3)<2
13.解:(1)由题意,得 解得m=3,∴点C的坐标为(3,4).∵一次函数y= kx+b经过点A(-3,0),C(3,4),∴ 解得
14.解:(1)把x=3代入 得y=5,∴点 B的坐标为(3,5).∵点B在一次函数y= kx+9的图象上,∴5=3k+9,解得 (2)把x=0代入 得y=9,∴点A的坐标为(0,9),即OA=9.设点Q的坐标为 则 解得 或 点Q的坐标为( ,3)或(
15.解:(1)50 1 (2)设. 把(4,200)代入 得200=4k ,解得 把(1,0),(3,200)代入 得 解得(3)令50t=100t-100,解得t=2.∴甲车经过2h被乙车追上.把t=2代入s =50t,得s =50×2=100,200-100=100(km).∴此时两车距离 B地还有100 km.
(时间:40 分钟 满分:100分)
一、选择题(每小题4分,共24分)
1.下列函数中,不是一次函数的是 ( )
A. y=-x+4
2.已知正比例函数y=kx的图象经过点( ),则k= ( )
A. B. C. D.5
3.当b<0时,一次函数y=2x-b的图象大致是 ( )
4.若一次函数y=(2m--1)x+2的值随x的增大而增大,则点 P(-m,m)所在象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知将直线y=x-1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是 ( )
A.经过第一、二、四象限
B.与x轴交于点(1,0)
C.与y轴交于点(0,1)
D. y随x的增大而减小
6.对于某个一次函数y= kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A. k>0 B. kb<0
C. k+b>0
二、填空题(每小题5分,共30分)
7.已知一次函数y=-x+2的图象经过点A(n,3),则n的值是 .
8.若函数 是关于 x 的正比例函数,则m+n= .
9.甲、乙两名同学观察完某个一次函数的图象后,分别得到下列结论:
甲:函数的图象经过点(0,1).
乙:y随x的增大而减小.
根据他们的叙述,写出满足上述结论的一个函数解析式: .
10.已知点 A(m,2),B(n,-3)在一次函数y= 的图象上,则m,n的大小关系是 m n(填“>”“<”或“=”).
11.如图,点 B 的坐标是(0,3),将△OAB沿x轴向右平移得到△CDE,点 B 的对应点 E 恰好落在直线y=2x--3上,则点A移动的距离是 .
12.已知 P 是直线y=-2x+4上的一个动点,若点 P 到两坐标轴的距离相等,则点P 的坐标是 .
三、解答题(共46分)
13.(8分)已知关于x的一次函数y=(1-2m)x+m+1的图象经过第一、二、三象限,求m的取值范围.
14.(10 分)在平面直角坐标系内有三点 A(--1,4),B(--3,2),C(0,6).
(1)求过其中两点的直线的函数解析式(选一种情形作答).
(2)判断A,B,C三点是否在同一条直线上,并说明理由.
15.(13分)如图,已知直线 与x轴、y轴分别交于点A,B,直线 与直线y= ax+b(a,b为常数,且a≠0)关于x轴对称,直线 y=ax+b与y 轴交于点C.
(1)求a,b的值.
(2)P 是直线AC 在x 轴上方的一个动点,当△ABP 的面积为 6 时,求点 P的坐标.
16.(15分)如图,直线 与x轴,y轴分别交于点 A(-3,0),B(0,3),直线 l : 与直线 l 相交于点
(1)求直线 l 和 l 的解析式.
(2)M为 y轴上一动点,连接 MA,MC,当 的值最小时,求点 M的坐标.
周测(19.2.2第4课时~19.3)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共24分)
1. 直线 y= ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程 ax+b=0的解为 ( )
A. x=0 B. x=1 C. x=2 D. x=3
2.如图,直线 y= ax+b(a≠0)过点 A,B,则不等式 ax+b>0的解集是 ( )
B. x>-3
C. x>0 D. x>4
3.如图,一次函数y=2x和y= ax+4的图象相交于点 A(m,3),则关于x,y的方程组 的解为 ( )
A.10° D.{x=2,
4.已知一次函数y=kx+b的图象如图所示,当x<1时,y的取值范围是 ( )
A.0
5.生物活动小组的同学们观察某植物生长,得到该植物的高度 y(cm)与观察时间x(天)的关系,并画出如图所示的图象(CD∥x轴),该植物的最高高度是 ( )
A. 50cm B. 20cm C.16 cm D.26 cm
6.某商场销售一种儿童滑板车,经市场调查,售价x(元)、每星期销量y(件)、单件利润w(元)之间的关系如图 1、图2 所示.若某星期该滑板车的单件利润为20元,则本星期该滑板车的销量为 ( )
A.94件 B.96件
C.1600件 D.1800件
二、填空题(每小题4分,共20分)
7.已知方程2x+1=-x+4的解是x=1,则在同一平面直角坐标系中直线 y=2x+1与y=--x+4的交点坐标是 .
8.如图,直线 y= kx+b(k,b是常数,k≠0)与直线 y=2 交于点 A(4,2),则关于x的不等式 kx+b<2的解集为 .
9.某公司急需用车,但又不准备买车,公司准备和一个个体车主或一家出租车公司签订月租车合同,他们的月收费y(元)与公司每月用车的路程x(千米)之间的关系如图所示(其中个体车主收费为 y 元,出租车公司收费为y 元),则当x 时,选用个体车主较划算.
10.我们规定:当k,b为常数(k≠0,b≠0,k≠b)时,一次函数y= kx+b与y= bx+k互为“交换函数”,例如y=4x+3的“交换函数”为 y=3x+4.则一次函数 y= kx+2与它的“交换函数”图象的交点横坐标为
11.一次函数y=-2x+4与y=x---2的图象与 y轴所围成的三角形的面积为 .
三、解答题(共56分)
12.(12分)已知一次函数y=--2x+4,解决下列问题:
(1)在所给平面直角坐标系中画出此函数的图象.
(2)根据图象回答:当x= 时,-2x+4=4.
(3)根据图象回答:当x 时,y>0.
13.(13分)如图,在平面直角坐标系中,一次函数 y=kx+b的图象与 x轴的交点为A(-3,0),与 y轴的交点为 B,且与正比例函数 的图象交于点C(m,4).
(1)求一次函数y= kx+b的解析式.
(2)关于x的不等式 的解集为 .
14.(14分)如图,在平面直角坐标系中,一次函数y=kx+9的图象与 y轴相交于点A,与x轴相交于点C,并与直线 相交于点B,其中点 B 的横坐标为3.
(1)求点 B 的坐标和k 的值.
(2)Q为直线y= kx+9上一动点,当点 Q运动到何位置时,△OBQ的面积等于 请求出点Q的坐标.
15.(17分)甲、乙两车沿相同的路线由 A 地到 B 地匀速前进,A,B两地间的路程为200km,甲、乙两车前进的路程分别为s (km),s (km),甲车出发后的时间为t(h),甲、乙两车前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:
(1)甲车的速度是 km/h,乙车比甲车晚出发 h.
(2)请分别求出甲、乙两车前进的路程s ,s 与甲车出发后的时间t之间的函数关系式.
(3)甲车经过多长时间被乙车追上 此时两车距离 B地还有多远
周测(19.2.1~19.2.2 第 3课时)
1. D 2. C 3. A 4. B 5. C 6. C 7.-1 8.2 9. y=-x+1(答案不唯一) 10.< 11.3 1 2.( , )或(4,-4)
13.解:∵一次函数y=(1-2m)x+m+1的图象经过第一、二、三象限 解得 ∴m的取值范围是-1<
14.解:(1)设过A(-1,4),B(-3,2)两点的直线AB的解析式为y=kx+b,则 解得 直线 AB 的解析式为y=x+5.(答案不唯一)(2)A,B,C三点不在同一条直线上.理由:当x=0时,y=0+5≠6,∴点C(0,6)不在直线AB上,即点A,B,C三点不在同一直线上.
15.解:(1)在 中,令x=0,则.y=-2.∴B(0,-2).令y=0,则 解得x=4.∴A(4,0).∵直线 与直线y= ax+b关于x轴对称,∴直线y= ax+b过点A(4,0)和点C(0,2).把点 A(4,0),C(0,2)代入 y= ax+b,得 解得 由(1)得,直线.y= ax+b的解析式为 2.设点 P 的横坐标为m,则 解得m=1.∴点 P的坐标为((1, ).
16.解:(1)把A(-3,0),B(0,3)代入 得 解得直线l 的解析式为y=x+3.把 代入y=x+3,得 把 代入 得 解得k =-3.∴直线l 的解析式为 y=-3x.(2)作点 A 关于y轴的对称点A',连接A'C,交 y轴于点M',连接AM',∵点A关于y轴的对称点为点A',∴MA=A'M.∴若MA+MC的值最小,则A'M+MC的值最小.当A',M,C三点共线时,MA+MC的值最小.∵A(-3,0),点 A 关于y轴的对称点为点A',∴A'(3,0).设直线A'C的解析式为y= mx+t,把A'(3,0),C(- , )代入y= mx+t,得 解得 直线 A'C的解析式为 令x=0,得 点M的坐标为(0, ).
周测(19.2.2第4课时~19.3)
1. C 2. B 3. A 4. D 5. C 6. D 7.(1,3) 8. x<4 9.>180010.1 11.6
12.解:(1)图略.(2)0 (3)<2
13.解:(1)由题意,得 解得m=3,∴点C的坐标为(3,4).∵一次函数y= kx+b经过点A(-3,0),C(3,4),∴ 解得
14.解:(1)把x=3代入 得y=5,∴点 B的坐标为(3,5).∵点B在一次函数y= kx+9的图象上,∴5=3k+9,解得 (2)把x=0代入 得y=9,∴点A的坐标为(0,9),即OA=9.设点Q的坐标为 则 解得 或 点Q的坐标为( ,3)或(
15.解:(1)50 1 (2)设. 把(4,200)代入 得200=4k ,解得 把(1,0),(3,200)代入 得 解得(3)令50t=100t-100,解得t=2.∴甲车经过2h被乙车追上.把t=2代入s =50t,得s =50×2=100,200-100=100(km).∴此时两车距离 B地还有100 km.
