期中模拟测试---人教版2024-2025学年八年级数学下册(含答案)
文档属性
| 名称 | 期中模拟测试---人教版2024-2025学年八年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 06:38:21 | ||
图片预览

文档简介
期中测试
(时间:100 分钟 满分:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.若二次根式 在实数范围内有意义,则x的取值范围是 ( )
2.下列各组数中,能作为直角三角形的三条边长的是 ( )
A.3,5,7 B.1, ,2 C.4,6,7 D.5,7,8
3.下列二次根式是最简二次根式的是 ( )
4.如果平行四边形的周长为120 cm,相邻两边长度之比为5:7,那么较长的边长为 ( )
A.35 cm B.28 cm C.42 cm D.25 cm
5.下列计算错误的是 ( )
6.如图,已知在菱形ABCD中,对角线AC,BD相交于点O,∠BAD=120°,AC=4,则该菱形的面积是 ( )
B.16 D.8
7.在如图所示的网格中,小正方形的边长均为1,A,B,C三点均在正方形的顶点上,则下列结论错误的是 ( )
A. S△ABC=10 B.∠BAC=90°
D.点 A 到直线 BC 的距离是 2
8.如图,在△ABC中,BC=26,且BD,CE分别是AC,AB上的高,F,G分别是BC,DE的中点.若ED=10,则 FG的长为 ( )
A.10 B.12 C.13 D.14
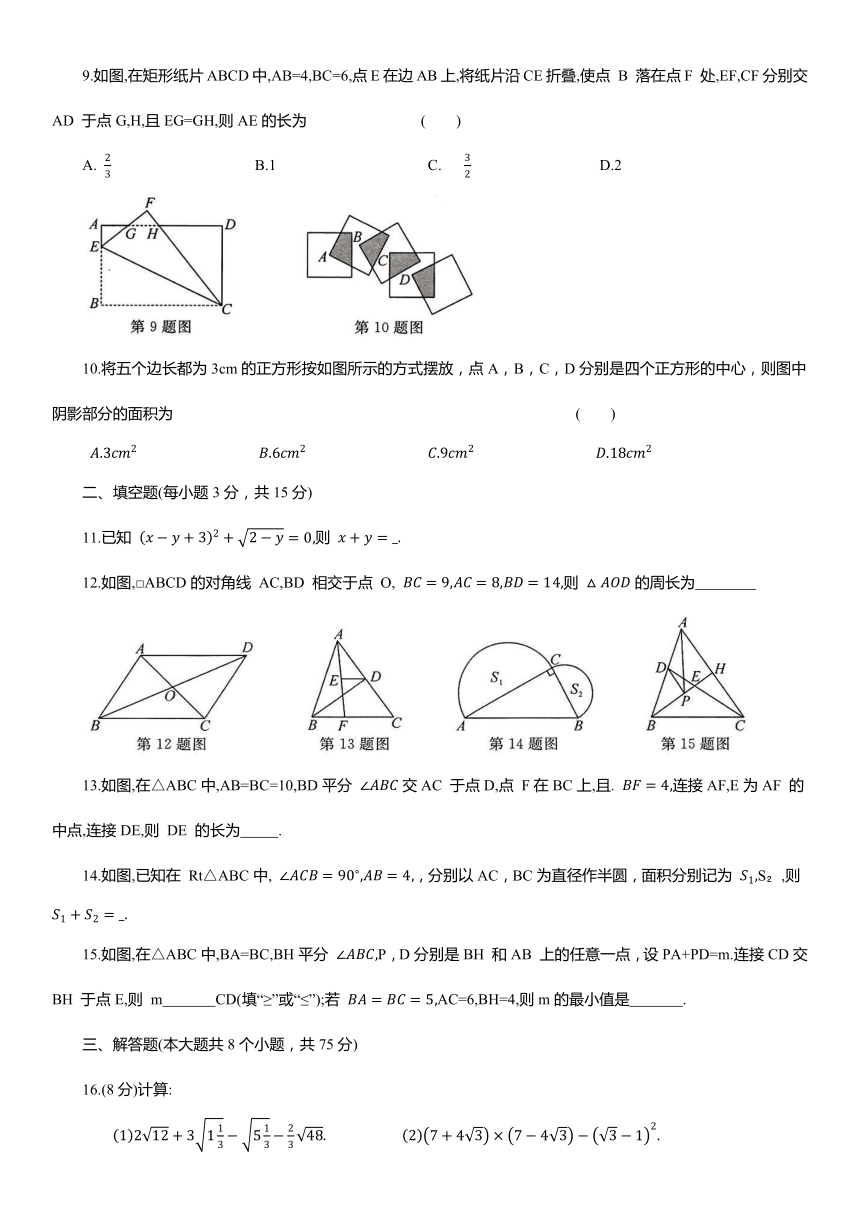
9.如图,在矩形纸片ABCD中,AB=4,BC=6,点E在边AB上,将纸片沿CE折叠,使点 B 落在点F 处,EF,CF分别交AD 于点G,H,且EG=GH,则AE的长为 ( )
A. B.1 C. D.2
10.将五个边长都为3cm的正方形按如图所示的方式摆放,点A,B,C,D分别是四个正方形的中心,则图中阴影部分的面积为 ( )
二、填空题(每小题3分,共15分)
11.已知 则
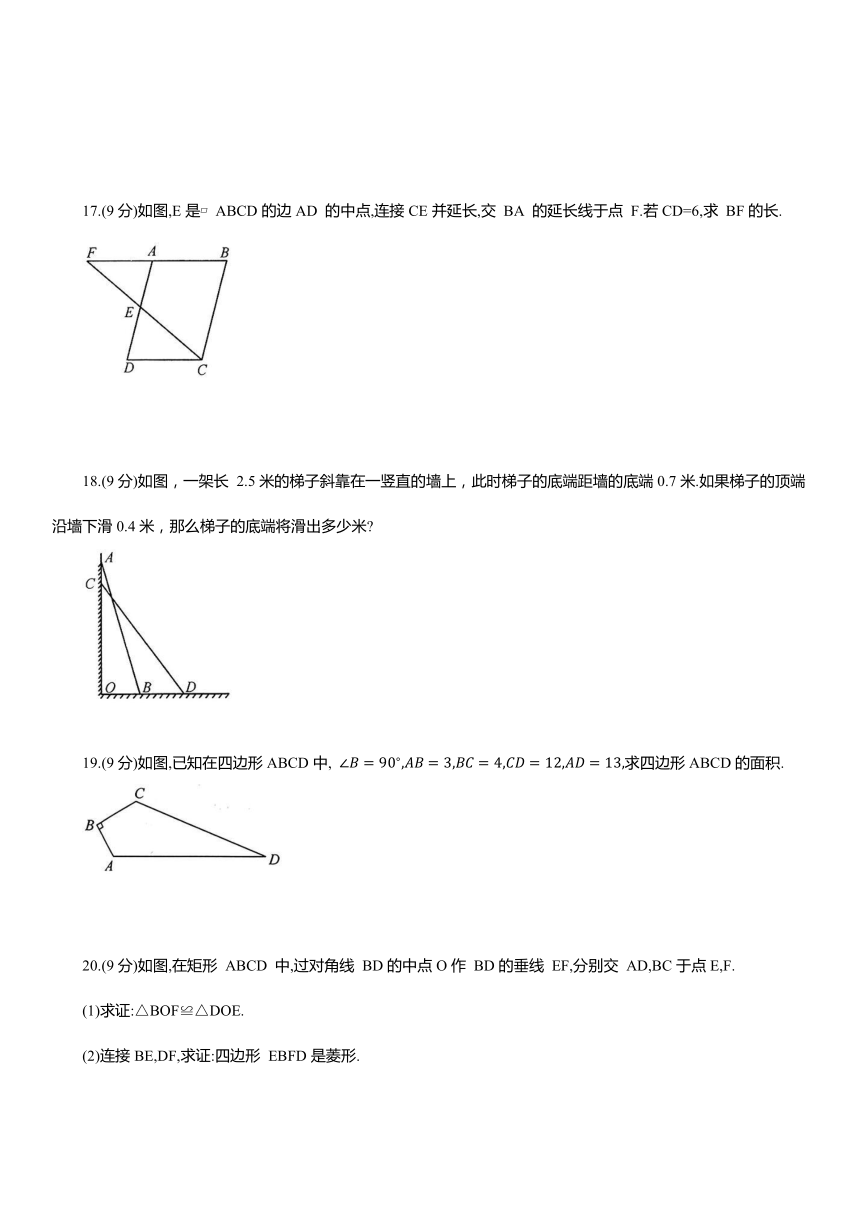
12.如图,□ABCD的对角线 AC,BD 相交于点 O, 则 的周长为
13.如图,在△ABC中,AB=BC=10,BD平分 交AC 于点D,点 F在BC上,且. 连接AF,E为AF 的中点,连接DE,则 DE 的长为 .
14.如图,已知在 Rt△ABC中, ,分别以AC,BC为直径作半圆,面积分别记为 S ,则
15.如图,在△ABC中,BA=BC,BH平分 P,D分别是BH 和AB 上的任意一点,设PA+PD=m.连接CD交BH 于点E,则 m CD(填“≥”或“≤”);若 AC=6,BH=4,则m的最小值是 .
三、解答题(本大题共8个小题,共75分)
16.(8分)计算:
17.(9分)如图,E是 ABCD的边AD 的中点,连接CE并延长,交 BA 的延长线于点 F.若CD=6,求 BF的长.
18.(9分)如图,一架长 2.5米的梯子斜靠在一竖直的墙上,此时梯子的底端距墙的底端0.7米.如果梯子的顶端沿墙下滑0.4米,那么梯子的底端将滑出多少米
19.(9分)如图,已知在四边形ABCD中, 求四边形ABCD的面积.
20.(9分)如图,在矩形 ABCD 中,过对角线 BD的中点O作 BD的垂线 EF,分别交 AD,BC于点E,F.
(1)求证:△BOF≌△DOE.
(2)连接BE,DF,求证:四边形 EBFD是菱形.
21.(10分)如图,在△ABC中,AD是边 BC上的中线,E是AD的中点,过点A作 交 BE的延长线于点 F,连接CF.
(1)求证:四边形 ADCF 是平行四边形.
(2)填空:
①当AB=AC时,四边形 ADCF 是 形.
②当∠BAC=90°时,四边形 ADCF 是 形.
22.(10分)阅读材料:
在进行二次根式的运算时,如遇到像 这样的式子,还需做进一步地化简:
方法一:
方法二:
这种将分母中的根号化去的过程叫作分母有理化.
解决问题:
(1)选择你喜欢的一种方法化简:
(2)下面是甲、乙两个同学对 分母有理化的过程(x≠y):
甲:
乙:
关于甲、乙两个同学的化简过程,下列说法正确的是 .
A.甲、乙都对 B.甲对,乙错 C.甲错,乙对 D.甲、乙都错
(3)化简:
23.(11分)综合与实践:
问题背景:在一次综合与实践课上,老师让同学们以两个全等的三角形纸片为操作对象,进行相关问题的研究,下面是创新小组在操作纸片过程中研究的问题,请解决这些问题.如图1,△ABC≌△DEF,其中.
操作与发现:
(1)创新小组将两张三角形纸片按如图2所示的方式放置后,经过观察发现四边形ACBF是矩形,请证明这个结论.
操作与探究:
(2)创新小组在图2的基础上,将△DEF 纸片沿AB 方向平移至图3的位置,其中点 E与AB 的中点重合,连接CE,BF,经过探究后发现四边形 BCEF 是菱形,请证明这个结论.
(3)创新小组在图3的基础上又进行了探究,将△DEF 纸片绕点E 逆时针旋转至DE 与BC平行的位置,如图4所示,连接AF,BF.创新小组经过观察与推理后发现四边形ACBF是矩形,请证明这个结论.
提出问题:
(4)请参照以上操作,在图2的基础上,通过平移构造出新图形,在图5中画出这个图形,标明字母,说明构图方法,写出你发现的结论,不必证明.
期中测试
1. A 2. B 3. D 4. A 5. D 6. C 7. A 8. B 9. B 10. C 11.112.20 13.3 14.2π 15.≥
16.解:(1)原式 (2)原式
17.解:∵E 是 ABCD的边AD 的中点,∴AE=DE.∵四边形ABCD是平行四边形,∴AB=CD=6,AB∥CD.∴∠F=∠DCE.在△AEF 和△DEC 中, ∴△AEF≌△DEC(AAS).∴AF=CD=6.∴BF=AB+AF=12.
18.解:依题意知AB=CD=2.5米,OB=0.7米,AC=0.4米.在Rt△AOB中,由勾股定理,得( =2.4(米),∴OC=OA-AC=2.4-0.4=2(米).在Rt△COD中,由勾股定理,得 5(米),∴BD=OD-OB=1.5-0.7=0.8(米).答:梯子的底端将滑出0.8米.
19.解:连接AC.在 Rt△ABC中,由勾股定理,得. .∠ACD=90°,即AC⊥CD.∴S四边形ABCD=S△ABC+S△ACD= AB.
20.证明:(1)∵四边形 ABCD 是矩形,∴AD∥BC.∴∠FBO=∠EDO.∵O是BD的中点,∴BO=DO.又∵∠FOB=∠EOD,∴△BOF≌△DOE(ASA).(2)∵△BOF≌△DOE,∴BF=DE.∵AD∥BC,即DE∥BF,∴四边形 EBFD是平行四边形.∵EF⊥BD,∴平行四边形EBFD是菱形.
21.解:(1)证明:∵AF∥BC,∴∠AFE=∠DBE.∵E是AD的中点,∴AE=DE.在△AEF 和△DEB中 AEF≌△DEB(AAS).∴AF=BD.∵AD是边BC上的中线,∴BD=DC.∴AF=DC.又∵AF∥BC,∴四边形ADCF是平行四边形.(2)①矩 ②菱
22.解:(1)方法一 方法二: (2)A(3)原式
23.解:(1)证明:∵△ABC≌△DEF,∴AC=DF=BF,BC=EF=AF.∴四边形ACBF 是平行四边形.∵∠ACB=90°,∴□ACBF是矩形.(2)证明:在 Rt△ABC中,∠ABC=60°,∴∠A=30°.∵△ABC≌△DEF,∴BC=EF,∠ABC=∠DEF.∴BC∥EF.∴四边形 BCEF是平行四边形.∵∠ACB=90°,∠A=30°,∴BC= AB.∵点E与AB的中点重合, =CE.∴□BCEF是菱形.(3)证明:在Rt△ABC中,∠ABC=60°,∴∠BAC=30°.∵△ABC≌△DEF,E是AB 的中点,∴EF=BC= AB=AE,∠DEF=60°.∵DE∥BC,∴∠BED=∠ABC=60°.∴∠AEF=180°-∠DEF-∠BED=60°.∴△AEF是等边三角形.∴∠EAF=60°,AF=AE.∴∠EAF=∠ABC=60°,AF=BC.∴AF∥BC ∴四边形ACBF是平行四边形.∵∠ACB=90°,∴□ACBF是矩形.(4)图略,将△DEF向下平移DF 的长度,使EF与CB 重合,得到四边形 ACDB,则四边形ACDB 为平行四边形.
(时间:100 分钟 满分:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.若二次根式 在实数范围内有意义,则x的取值范围是 ( )
2.下列各组数中,能作为直角三角形的三条边长的是 ( )
A.3,5,7 B.1, ,2 C.4,6,7 D.5,7,8
3.下列二次根式是最简二次根式的是 ( )
4.如果平行四边形的周长为120 cm,相邻两边长度之比为5:7,那么较长的边长为 ( )
A.35 cm B.28 cm C.42 cm D.25 cm
5.下列计算错误的是 ( )
6.如图,已知在菱形ABCD中,对角线AC,BD相交于点O,∠BAD=120°,AC=4,则该菱形的面积是 ( )
B.16 D.8
7.在如图所示的网格中,小正方形的边长均为1,A,B,C三点均在正方形的顶点上,则下列结论错误的是 ( )
A. S△ABC=10 B.∠BAC=90°
D.点 A 到直线 BC 的距离是 2
8.如图,在△ABC中,BC=26,且BD,CE分别是AC,AB上的高,F,G分别是BC,DE的中点.若ED=10,则 FG的长为 ( )
A.10 B.12 C.13 D.14
9.如图,在矩形纸片ABCD中,AB=4,BC=6,点E在边AB上,将纸片沿CE折叠,使点 B 落在点F 处,EF,CF分别交AD 于点G,H,且EG=GH,则AE的长为 ( )
A. B.1 C. D.2
10.将五个边长都为3cm的正方形按如图所示的方式摆放,点A,B,C,D分别是四个正方形的中心,则图中阴影部分的面积为 ( )
二、填空题(每小题3分,共15分)
11.已知 则
12.如图,□ABCD的对角线 AC,BD 相交于点 O, 则 的周长为
13.如图,在△ABC中,AB=BC=10,BD平分 交AC 于点D,点 F在BC上,且. 连接AF,E为AF 的中点,连接DE,则 DE 的长为 .
14.如图,已知在 Rt△ABC中, ,分别以AC,BC为直径作半圆,面积分别记为 S ,则
15.如图,在△ABC中,BA=BC,BH平分 P,D分别是BH 和AB 上的任意一点,设PA+PD=m.连接CD交BH 于点E,则 m CD(填“≥”或“≤”);若 AC=6,BH=4,则m的最小值是 .
三、解答题(本大题共8个小题,共75分)
16.(8分)计算:
17.(9分)如图,E是 ABCD的边AD 的中点,连接CE并延长,交 BA 的延长线于点 F.若CD=6,求 BF的长.
18.(9分)如图,一架长 2.5米的梯子斜靠在一竖直的墙上,此时梯子的底端距墙的底端0.7米.如果梯子的顶端沿墙下滑0.4米,那么梯子的底端将滑出多少米
19.(9分)如图,已知在四边形ABCD中, 求四边形ABCD的面积.
20.(9分)如图,在矩形 ABCD 中,过对角线 BD的中点O作 BD的垂线 EF,分别交 AD,BC于点E,F.
(1)求证:△BOF≌△DOE.
(2)连接BE,DF,求证:四边形 EBFD是菱形.
21.(10分)如图,在△ABC中,AD是边 BC上的中线,E是AD的中点,过点A作 交 BE的延长线于点 F,连接CF.
(1)求证:四边形 ADCF 是平行四边形.
(2)填空:
①当AB=AC时,四边形 ADCF 是 形.
②当∠BAC=90°时,四边形 ADCF 是 形.
22.(10分)阅读材料:
在进行二次根式的运算时,如遇到像 这样的式子,还需做进一步地化简:
方法一:
方法二:
这种将分母中的根号化去的过程叫作分母有理化.
解决问题:
(1)选择你喜欢的一种方法化简:
(2)下面是甲、乙两个同学对 分母有理化的过程(x≠y):
甲:
乙:
关于甲、乙两个同学的化简过程,下列说法正确的是 .
A.甲、乙都对 B.甲对,乙错 C.甲错,乙对 D.甲、乙都错
(3)化简:
23.(11分)综合与实践:
问题背景:在一次综合与实践课上,老师让同学们以两个全等的三角形纸片为操作对象,进行相关问题的研究,下面是创新小组在操作纸片过程中研究的问题,请解决这些问题.如图1,△ABC≌△DEF,其中.
操作与发现:
(1)创新小组将两张三角形纸片按如图2所示的方式放置后,经过观察发现四边形ACBF是矩形,请证明这个结论.
操作与探究:
(2)创新小组在图2的基础上,将△DEF 纸片沿AB 方向平移至图3的位置,其中点 E与AB 的中点重合,连接CE,BF,经过探究后发现四边形 BCEF 是菱形,请证明这个结论.
(3)创新小组在图3的基础上又进行了探究,将△DEF 纸片绕点E 逆时针旋转至DE 与BC平行的位置,如图4所示,连接AF,BF.创新小组经过观察与推理后发现四边形ACBF是矩形,请证明这个结论.
提出问题:
(4)请参照以上操作,在图2的基础上,通过平移构造出新图形,在图5中画出这个图形,标明字母,说明构图方法,写出你发现的结论,不必证明.
期中测试
1. A 2. B 3. D 4. A 5. D 6. C 7. A 8. B 9. B 10. C 11.112.20 13.3 14.2π 15.≥
16.解:(1)原式 (2)原式
17.解:∵E 是 ABCD的边AD 的中点,∴AE=DE.∵四边形ABCD是平行四边形,∴AB=CD=6,AB∥CD.∴∠F=∠DCE.在△AEF 和△DEC 中, ∴△AEF≌△DEC(AAS).∴AF=CD=6.∴BF=AB+AF=12.
18.解:依题意知AB=CD=2.5米,OB=0.7米,AC=0.4米.在Rt△AOB中,由勾股定理,得( =2.4(米),∴OC=OA-AC=2.4-0.4=2(米).在Rt△COD中,由勾股定理,得 5(米),∴BD=OD-OB=1.5-0.7=0.8(米).答:梯子的底端将滑出0.8米.
19.解:连接AC.在 Rt△ABC中,由勾股定理,得. .∠ACD=90°,即AC⊥CD.∴S四边形ABCD=S△ABC+S△ACD= AB.
20.证明:(1)∵四边形 ABCD 是矩形,∴AD∥BC.∴∠FBO=∠EDO.∵O是BD的中点,∴BO=DO.又∵∠FOB=∠EOD,∴△BOF≌△DOE(ASA).(2)∵△BOF≌△DOE,∴BF=DE.∵AD∥BC,即DE∥BF,∴四边形 EBFD是平行四边形.∵EF⊥BD,∴平行四边形EBFD是菱形.
21.解:(1)证明:∵AF∥BC,∴∠AFE=∠DBE.∵E是AD的中点,∴AE=DE.在△AEF 和△DEB中 AEF≌△DEB(AAS).∴AF=BD.∵AD是边BC上的中线,∴BD=DC.∴AF=DC.又∵AF∥BC,∴四边形ADCF是平行四边形.(2)①矩 ②菱
22.解:(1)方法一 方法二: (2)A(3)原式
23.解:(1)证明:∵△ABC≌△DEF,∴AC=DF=BF,BC=EF=AF.∴四边形ACBF 是平行四边形.∵∠ACB=90°,∴□ACBF是矩形.(2)证明:在 Rt△ABC中,∠ABC=60°,∴∠A=30°.∵△ABC≌△DEF,∴BC=EF,∠ABC=∠DEF.∴BC∥EF.∴四边形 BCEF是平行四边形.∵∠ACB=90°,∠A=30°,∴BC= AB.∵点E与AB的中点重合, =CE.∴□BCEF是菱形.(3)证明:在Rt△ABC中,∠ABC=60°,∴∠BAC=30°.∵△ABC≌△DEF,E是AB 的中点,∴EF=BC= AB=AE,∠DEF=60°.∵DE∥BC,∴∠BED=∠ABC=60°.∴∠AEF=180°-∠DEF-∠BED=60°.∴△AEF是等边三角形.∴∠EAF=60°,AF=AE.∴∠EAF=∠ABC=60°,AF=BC.∴AF∥BC ∴四边形ACBF是平行四边形.∵∠ACB=90°,∴□ACBF是矩形.(4)图略,将△DEF向下平移DF 的长度,使EF与CB 重合,得到四边形 ACDB,则四边形ACDB 为平行四边形.
同课章节目录
