第18章 平行四边形 单元测试 (含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第18章 平行四边形 单元测试 (含答案) 2024-2025学年人教版八年级数学下册 | 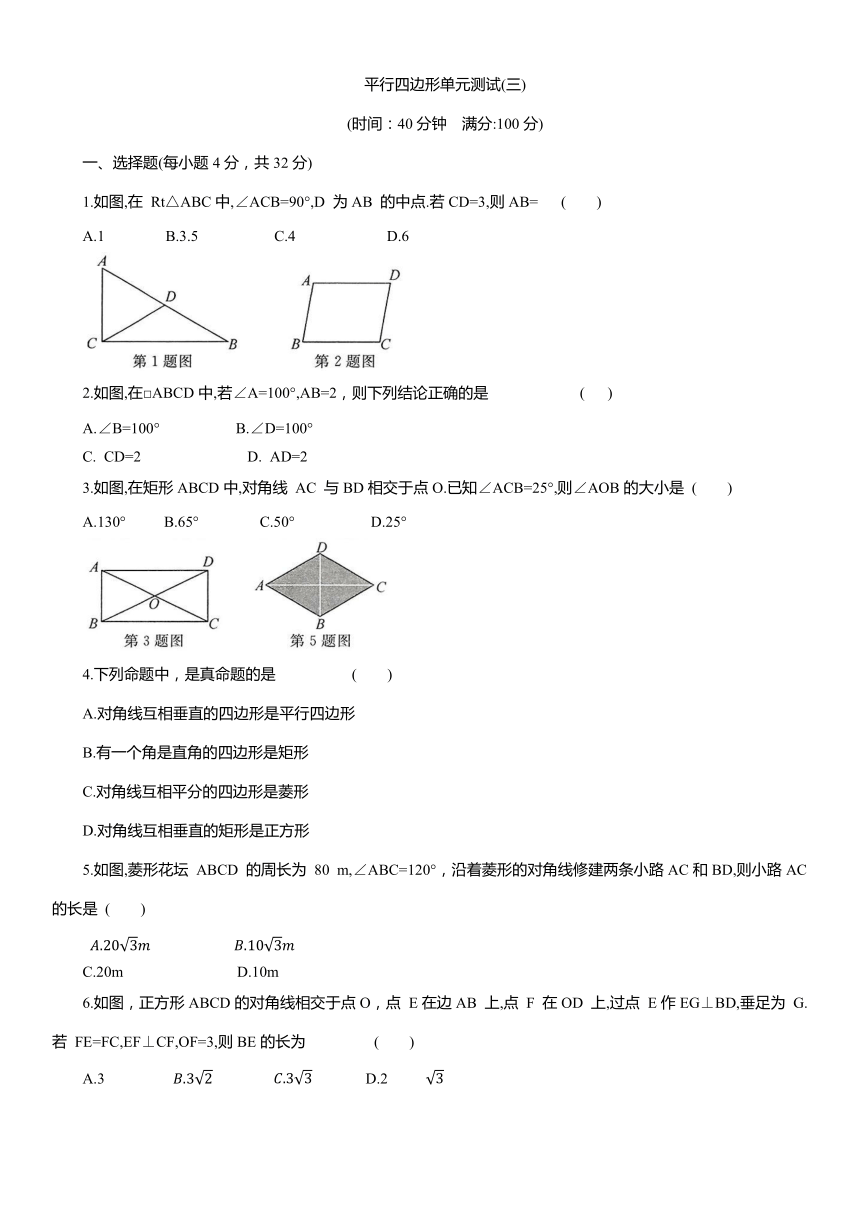 | |
| 格式 | docx | ||
| 文件大小 | 116.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 06:40:19 | ||
图片预览


文档简介
平行四边形单元测试(三)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.如图,在 Rt△ABC中,∠ACB=90°,D 为AB 的中点.若CD=3,则AB= ( )
A.1 B.3.5 C.4 D.6
2.如图,在□ABCD中,若∠A=100°,AB=2,则下列结论正确的是 ( )
A.∠B=100° B.∠D=100°
C. CD=2 D. AD=2
3.如图,在矩形ABCD中,对角线 AC 与BD相交于点O.已知∠ACB=25°,则∠AOB的大小是 ( )
A.130° B.65° C.50° D.25°
4.下列命题中,是真命题的是 ( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
5.如图,菱形花坛 ABCD 的周长为 80 m,∠ABC=120°,沿着菱形的对角线修建两条小路AC和BD,则小路AC的长是 ( )
C.20m D.10m
6.如图,正方形ABCD的对角线相交于点O,点 E在边AB 上,点 F 在OD 上,过点 E作EG⊥BD,垂足为 G.若 FE=FC,EF⊥CF,OF=3,则BE的长为 ( )
A.3 D.2
7.如图,在矩形AOBD中,点 D 的坐标是(1,3),则AB的长为 ( )
A.3 B. C.
8.如图,在平面直角坐标系中,四边形OABC是菱形,∠AOC=120°,点 B 的坐标为(6,0),点 P 从点O 出发,在菱形 OABC的边上以2个单位长度/秒的速度,沿O→A→B→C→O→A…的路线作循环运动,则第 2 024秒时,点P 的坐标为 ( )
二、填空题(每小题5分,共25分)
9.如图,把两根钢条OA,OB的一个端点连在一起,C,D 分别是 OA,OB 的中点.若 CD=4 cm,则该工件内槽宽AB的长为 cm.
10.如图,四边形ABCD的对角线 AC,BD相交于点 O,且AB=CD,∠ABD=∠CDB,请再添加一个条件: ,使四边形ABCD是矩形(写出一个即可).
11.如图,在 ABCD中,AB=3,BC=5,以点 B 为圆心、任意长为半径作弧,分别交BA,BC于点 P,Q,再分别以点 P,Q为圆心、大于 PQ的长为半径作弧,两弧在∠ABC内交于点 M,连接 BM并延长,交AD 于点 E,则 DE 的长为 .
如图,菱形 ABCD的对角线AC,BD相交于点O,H 为边AB 上的一点,∠BHD=90°,连接OH.若OA=5,OH=2,则菱形ABCD的面积为 .
13.如图,在矩形 ABCD中,AD=2,∠BAC=30°,E 是边 AD 的中点,F 是 CD 上一点,连接 EF,将△DEF 沿 EF 折叠,使点 D 落在矩形内的点 G处.若点G恰好在矩形的对角线上,则DF 的长为 .
三、解答题(共43分)
14.(13 分)如图,将 ABCD的边AB 延长至点 E,使 AB=BE,连接 DE,EC,DE 交BC 于点O.
(1)求证:四边形 BECD 是平行四边形.
(2)连接 BD,若∠BOD=2∠A,求证:四边形 BECD 是矩形.
15.(14分)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED 是菱形.
(2)若BC=3,DC=2,求四边形OCED的面积.
16.(16 分)如图 1,在□ABCD 中,AD =9 cm,CD=3 cm,∠B=45°,点 M,N分别以点 A,C 为起点,沿 AD,CB 以1 cm/s的速度运动,M,N 两点同时出发.设点 M,N运动的时间为t s(0≤t≤9).
(1)求边 BC上高AE 的长度.
(2)连接AN,CM,当t为何值时,四边形AMCN 为菱形
(3)如图2,作 MP⊥BC于点P,NQ⊥AD于点 Q,当t为何值时,四边形MPNQ为正方形
单元测试(三) 平行四边形
1. D 2. C 3. C 4. D 5. A 6. B 7. D 8. B 9.8 10.∠ABC=90°(答案不唯一)11.2 12.20 13. 或
14.证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.又∵AB=BE,∴BE=CD.又∵AE∥CD,∴四边形BECD是平行四边形.(2)由(1)知,四边形BECD 是平行四边形,∴OD=OE,OC=OB.∵四边形ABCD是平行四边形,∴∠A=∠OCD.又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,∴∠OCD=∠ODC.∴OC=OD.∴OC+OB=OD+OE,即BC=ED.∴平行四边形BECD为矩形.
15.解:(1)证明:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形.∵矩形ABCD的对角线AC,BD相交于点O,∴AC=BD,OC ∴平行四边形OCED 是菱形.(2)∵四边形ABCD是矩形,BC=3,DC=2,∴OA=OB=OC= ·四边形OCED是菱形,
16.解:(1)∵四边形 ABCD 是平行四边形,∴AB=CD=3 cm.在Rt△ABE中,∵∠AEB=90°,∠B=45°.∴AE=BE.∴AE=3cm.(2)由题意,得 AM=CN=t cm.∵AM∥CN,∴四边形AMCN为平行四边形.∴当AN=AM时,平行四边形 AMCN为菱形.∵BE=AE=3cm,∴EN=BC-BE-CN=9-3-t=(6- 解得 故当t的值为 时,四边形 AMCN 为菱形.(3)∵MP⊥BC,NQ⊥AD,QM∥NP,∴∠MPN=∠PMQ=∠NQM=90°.∴四边形 MPNQ为矩形.∴当QM=QN时,矩形 MPNQ为正方形.∵AM=CN=t cm,BE=3cm,∴AQ=EN=BC-BE-CN=9-3-t=(6-t) cm.∴QM=|t-(6-t)|=|2t-6| cm.∵QN=AE=3cm,∴|2t-6|=3,解得t=4.5或t=1.5.故当t的值为4.5或1.5时,四边形 MPNQ为正方形.
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.如图,在 Rt△ABC中,∠ACB=90°,D 为AB 的中点.若CD=3,则AB= ( )
A.1 B.3.5 C.4 D.6
2.如图,在□ABCD中,若∠A=100°,AB=2,则下列结论正确的是 ( )
A.∠B=100° B.∠D=100°
C. CD=2 D. AD=2
3.如图,在矩形ABCD中,对角线 AC 与BD相交于点O.已知∠ACB=25°,则∠AOB的大小是 ( )
A.130° B.65° C.50° D.25°
4.下列命题中,是真命题的是 ( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
5.如图,菱形花坛 ABCD 的周长为 80 m,∠ABC=120°,沿着菱形的对角线修建两条小路AC和BD,则小路AC的长是 ( )
C.20m D.10m
6.如图,正方形ABCD的对角线相交于点O,点 E在边AB 上,点 F 在OD 上,过点 E作EG⊥BD,垂足为 G.若 FE=FC,EF⊥CF,OF=3,则BE的长为 ( )
A.3 D.2
7.如图,在矩形AOBD中,点 D 的坐标是(1,3),则AB的长为 ( )
A.3 B. C.
8.如图,在平面直角坐标系中,四边形OABC是菱形,∠AOC=120°,点 B 的坐标为(6,0),点 P 从点O 出发,在菱形 OABC的边上以2个单位长度/秒的速度,沿O→A→B→C→O→A…的路线作循环运动,则第 2 024秒时,点P 的坐标为 ( )
二、填空题(每小题5分,共25分)
9.如图,把两根钢条OA,OB的一个端点连在一起,C,D 分别是 OA,OB 的中点.若 CD=4 cm,则该工件内槽宽AB的长为 cm.
10.如图,四边形ABCD的对角线 AC,BD相交于点 O,且AB=CD,∠ABD=∠CDB,请再添加一个条件: ,使四边形ABCD是矩形(写出一个即可).
11.如图,在 ABCD中,AB=3,BC=5,以点 B 为圆心、任意长为半径作弧,分别交BA,BC于点 P,Q,再分别以点 P,Q为圆心、大于 PQ的长为半径作弧,两弧在∠ABC内交于点 M,连接 BM并延长,交AD 于点 E,则 DE 的长为 .
如图,菱形 ABCD的对角线AC,BD相交于点O,H 为边AB 上的一点,∠BHD=90°,连接OH.若OA=5,OH=2,则菱形ABCD的面积为 .
13.如图,在矩形 ABCD中,AD=2,∠BAC=30°,E 是边 AD 的中点,F 是 CD 上一点,连接 EF,将△DEF 沿 EF 折叠,使点 D 落在矩形内的点 G处.若点G恰好在矩形的对角线上,则DF 的长为 .
三、解答题(共43分)
14.(13 分)如图,将 ABCD的边AB 延长至点 E,使 AB=BE,连接 DE,EC,DE 交BC 于点O.
(1)求证:四边形 BECD 是平行四边形.
(2)连接 BD,若∠BOD=2∠A,求证:四边形 BECD 是矩形.
15.(14分)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED 是菱形.
(2)若BC=3,DC=2,求四边形OCED的面积.
16.(16 分)如图 1,在□ABCD 中,AD =9 cm,CD=3 cm,∠B=45°,点 M,N分别以点 A,C 为起点,沿 AD,CB 以1 cm/s的速度运动,M,N 两点同时出发.设点 M,N运动的时间为t s(0≤t≤9).
(1)求边 BC上高AE 的长度.
(2)连接AN,CM,当t为何值时,四边形AMCN 为菱形
(3)如图2,作 MP⊥BC于点P,NQ⊥AD于点 Q,当t为何值时,四边形MPNQ为正方形
单元测试(三) 平行四边形
1. D 2. C 3. C 4. D 5. A 6. B 7. D 8. B 9.8 10.∠ABC=90°(答案不唯一)11.2 12.20 13. 或
14.证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.又∵AB=BE,∴BE=CD.又∵AE∥CD,∴四边形BECD是平行四边形.(2)由(1)知,四边形BECD 是平行四边形,∴OD=OE,OC=OB.∵四边形ABCD是平行四边形,∴∠A=∠OCD.又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,∴∠OCD=∠ODC.∴OC=OD.∴OC+OB=OD+OE,即BC=ED.∴平行四边形BECD为矩形.
15.解:(1)证明:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形.∵矩形ABCD的对角线AC,BD相交于点O,∴AC=BD,OC ∴平行四边形OCED 是菱形.(2)∵四边形ABCD是矩形,BC=3,DC=2,∴OA=OB=OC= ·四边形OCED是菱形,
16.解:(1)∵四边形 ABCD 是平行四边形,∴AB=CD=3 cm.在Rt△ABE中,∵∠AEB=90°,∠B=45°.∴AE=BE.∴AE=3cm.(2)由题意,得 AM=CN=t cm.∵AM∥CN,∴四边形AMCN为平行四边形.∴当AN=AM时,平行四边形 AMCN为菱形.∵BE=AE=3cm,∴EN=BC-BE-CN=9-3-t=(6- 解得 故当t的值为 时,四边形 AMCN 为菱形.(3)∵MP⊥BC,NQ⊥AD,QM∥NP,∴∠MPN=∠PMQ=∠NQM=90°.∴四边形 MPNQ为矩形.∴当QM=QN时,矩形 MPNQ为正方形.∵AM=CN=t cm,BE=3cm,∴AQ=EN=BC-BE-CN=9-3-t=(6-t) cm.∴QM=|t-(6-t)|=|2t-6| cm.∵QN=AE=3cm,∴|2t-6|=3,解得t=4.5或t=1.5.故当t的值为4.5或1.5时,四边形 MPNQ为正方形.
