第十七章勾股定理单元测试 (含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章勾股定理单元测试 (含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 112.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 08:44:12 | ||
图片预览

文档简介
勾股定理单元测试(二)
(时间:40分钟 满分:100分)
一、选择题(每小题5分,共30分)
1.以下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是 ( )
B.2,3,4
C.6,7,8 D.9,12,15
2.点A(--3,-4)到原点的距离为 ( )
A.3 B.4 C.5 D.7
3.已知一个直角三角形的两条边长分别是6和8,则第三边长是 ( )
A.10或2 B.2
C.8 D.10
4.如图,在水塔O的东北方向24m处有一抽水站A,在水塔的东南方向 18 m处有一建筑工地 B,在AB 间建一条笔直的水管,则水管AB 的长为 ( )
A.40m B.45 m C.30m D.35 m
5.如图,在3×3的正方形网格中,每个小正方形边长为1,点 A,B,C,D均为格点,以点 A 为圆心,AB 的长为半径作弧,交网格线CD 于点E,则C,E两点间的距离为( )
A.
6.将一根长为24 cm的筷子置于底面直径为12 cm,高为5cm 的圆柱形水杯中,如图.设筷子露在杯子外面的长度为 h cm,则 h的取值范围是 ( )
A. h≤19
B.11≤h≤19
C.12≤h≤19
D.13≤h≤19
二、填空题(每小题5分,共35分)
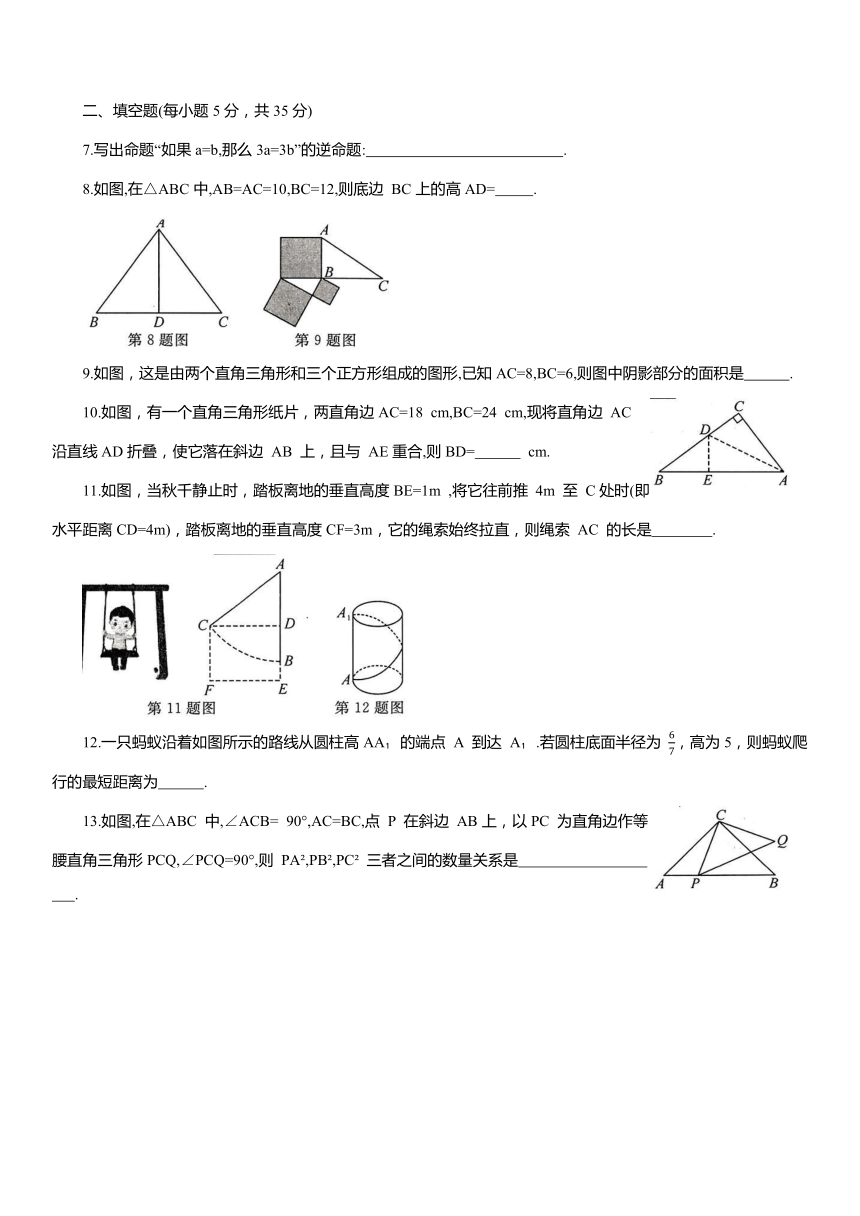
7.写出命题“如果a=b,那么3a=3b”的逆命题: .
8.如图,在△ABC中,AB=AC=10,BC=12,则底边 BC上的高AD= .
9.如图,这是由两个直角三角形和三个正方形组成的图形,已知AC=8,BC=6,则图中阴影部分的面积是 .
10.如图,有一个直角三角形纸片,两直角边AC=18 cm,BC=24 cm,现将直角边 AC 沿直线AD折叠,使它落在斜边 AB 上,且与 AE重合,则BD= cm.
11.如图,当秋千静止时,踏板离地的垂直高度BE=1m ,将它往前推 4m 至 C处时(即水平距离CD=4m),踏板离地的垂直高度CF=3m,它的绳索始终拉直,则绳索 AC 的长是 .
12.一只蚂蚁沿着如图所示的路线从圆柱高AA 的端点 A 到达 A .若圆柱底面半径为 ,高为5,则蚂蚁爬行的最短距离为 .
13.如图,在△ABC 中,∠ACB= 90°,AC=BC,点 P 在斜边 AB上,以PC 为直角边作等腰直角三角形PCQ,∠PCQ=90°,则 PA ,PB ,PC 三者之间的数量关系是 .
三、解答题(共35分)
14.(8分)如图,在△ABC中,CD⊥AB 于点D,AC=20,CD=12,BD=9.求 AB与 BC的长.
15.(8分)如图,每个小方格的边长都为1.
(1)求图中格点四边形ABCD 的面积.
(2)请探究 AD 与CD 的位置关系,并说明理由.
16.(9 分)如图,∠AOB=90°,OA=45 cm,OB=15 cm,一机器人在点 B 处看见一个小球从点 A 出发沿着AO 方向匀速滚向点O,机器人立即从点 B 出发,沿直线匀速前进拦截小球,恰好在点 C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程 BC 是多少
17.(10分)新定义:对角线互相垂直的四边形叫做“垂美四边形”.
(1)如图1,已知四边形 ABCD 是垂美四边形.若 AB=c,BC=d,CD=a,DA=b,探究a,b,c,d的数量关系.
(2)如图2,在长方形ABCD中,AB=6,P是边AD 上一点,且 AP=2PD,CP⊥BD,求 AD的长.
单元测试(二) 勾股定理
1. D 2. C 3. A 4. C 5. B 6. B 7.如果3a=3b,那么a=b 8.89.56 10.15 11.5 m 12.13 13.
14.解:∵CD⊥AB,∴∠CDB=∠CDA=90°.在Rt△BDC中,CD + 即 ,解得 BC=15.在 Rt△ADC 中,AD 即 ,解得AD=16.∴AB=AD+BD=16+9=25.
15.解:(1 S四边形ABCD=S△ADC+S△ABC=5+7.5=12.5.(2)AD⊥CD.理由:由勾 +CD =( ) +(2 ) =25=AC .∴△ACD为直角三角形,且∠ADC=90°.∴AD⊥CD.
16.解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,∴BC=CA.设AC= xcm,则OC=(45-x) cm.由勾股定理可知, ,解得x=25.答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25 cm.
17.解:(1)∵四边形 ABCD是垂美四边形,∴AC⊥BD.∴∠AOD=∠AOB=∠BOC=∠COD=90°.由勾股定理,得 - 即 (2)连接 PB.设 PD=x,则AP=2x,AD=3x.∵BD⊥PC,∴PD +BC =PB +CD .∵四边形ABCD是长方形,∴AB=CD=6,BC=AD=3x.∴x + 解得 (负值舍去).∴AD=3x=
(时间:40分钟 满分:100分)
一、选择题(每小题5分,共30分)
1.以下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是 ( )
B.2,3,4
C.6,7,8 D.9,12,15
2.点A(--3,-4)到原点的距离为 ( )
A.3 B.4 C.5 D.7
3.已知一个直角三角形的两条边长分别是6和8,则第三边长是 ( )
A.10或2 B.2
C.8 D.10
4.如图,在水塔O的东北方向24m处有一抽水站A,在水塔的东南方向 18 m处有一建筑工地 B,在AB 间建一条笔直的水管,则水管AB 的长为 ( )
A.40m B.45 m C.30m D.35 m
5.如图,在3×3的正方形网格中,每个小正方形边长为1,点 A,B,C,D均为格点,以点 A 为圆心,AB 的长为半径作弧,交网格线CD 于点E,则C,E两点间的距离为( )
A.
6.将一根长为24 cm的筷子置于底面直径为12 cm,高为5cm 的圆柱形水杯中,如图.设筷子露在杯子外面的长度为 h cm,则 h的取值范围是 ( )
A. h≤19
B.11≤h≤19
C.12≤h≤19
D.13≤h≤19
二、填空题(每小题5分,共35分)
7.写出命题“如果a=b,那么3a=3b”的逆命题: .
8.如图,在△ABC中,AB=AC=10,BC=12,则底边 BC上的高AD= .
9.如图,这是由两个直角三角形和三个正方形组成的图形,已知AC=8,BC=6,则图中阴影部分的面积是 .
10.如图,有一个直角三角形纸片,两直角边AC=18 cm,BC=24 cm,现将直角边 AC 沿直线AD折叠,使它落在斜边 AB 上,且与 AE重合,则BD= cm.
11.如图,当秋千静止时,踏板离地的垂直高度BE=1m ,将它往前推 4m 至 C处时(即水平距离CD=4m),踏板离地的垂直高度CF=3m,它的绳索始终拉直,则绳索 AC 的长是 .
12.一只蚂蚁沿着如图所示的路线从圆柱高AA 的端点 A 到达 A .若圆柱底面半径为 ,高为5,则蚂蚁爬行的最短距离为 .
13.如图,在△ABC 中,∠ACB= 90°,AC=BC,点 P 在斜边 AB上,以PC 为直角边作等腰直角三角形PCQ,∠PCQ=90°,则 PA ,PB ,PC 三者之间的数量关系是 .
三、解答题(共35分)
14.(8分)如图,在△ABC中,CD⊥AB 于点D,AC=20,CD=12,BD=9.求 AB与 BC的长.
15.(8分)如图,每个小方格的边长都为1.
(1)求图中格点四边形ABCD 的面积.
(2)请探究 AD 与CD 的位置关系,并说明理由.
16.(9 分)如图,∠AOB=90°,OA=45 cm,OB=15 cm,一机器人在点 B 处看见一个小球从点 A 出发沿着AO 方向匀速滚向点O,机器人立即从点 B 出发,沿直线匀速前进拦截小球,恰好在点 C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程 BC 是多少
17.(10分)新定义:对角线互相垂直的四边形叫做“垂美四边形”.
(1)如图1,已知四边形 ABCD 是垂美四边形.若 AB=c,BC=d,CD=a,DA=b,探究a,b,c,d的数量关系.
(2)如图2,在长方形ABCD中,AB=6,P是边AD 上一点,且 AP=2PD,CP⊥BD,求 AD的长.
单元测试(二) 勾股定理
1. D 2. C 3. A 4. C 5. B 6. B 7.如果3a=3b,那么a=b 8.89.56 10.15 11.5 m 12.13 13.
14.解:∵CD⊥AB,∴∠CDB=∠CDA=90°.在Rt△BDC中,CD + 即 ,解得 BC=15.在 Rt△ADC 中,AD 即 ,解得AD=16.∴AB=AD+BD=16+9=25.
15.解:(1 S四边形ABCD=S△ADC+S△ABC=5+7.5=12.5.(2)AD⊥CD.理由:由勾 +CD =( ) +(2 ) =25=AC .∴△ACD为直角三角形,且∠ADC=90°.∴AD⊥CD.
16.解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,∴BC=CA.设AC= xcm,则OC=(45-x) cm.由勾股定理可知, ,解得x=25.答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25 cm.
17.解:(1)∵四边形 ABCD是垂美四边形,∴AC⊥BD.∴∠AOD=∠AOB=∠BOC=∠COD=90°.由勾股定理,得 - 即 (2)连接 PB.设 PD=x,则AP=2x,AD=3x.∵BD⊥PC,∴PD +BC =PB +CD .∵四边形ABCD是长方形,∴AB=CD=6,BC=AD=3x.∴x + 解得 (负值舍去).∴AD=3x=
