【小升初真题汇编】查漏补缺专题09圆柱与圆锥(含答案)-2025年小学数学通用版
文档属性
| 名称 | 【小升初真题汇编】查漏补缺专题09圆柱与圆锥(含答案)-2025年小学数学通用版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 16:12:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【小升初真题汇编】查漏补缺专题09圆柱与圆锥-2025年小学数学通用版
一.选择题(共8小题)
1.(2025春 济南校级期末)把一个底面积为3.14cm2、高为10cm的圆柱形橡皮泥捏成一个底面积为12.56cm2的圆柱,高变为( )cm。
A.20 B.10 C.5 D.2.5
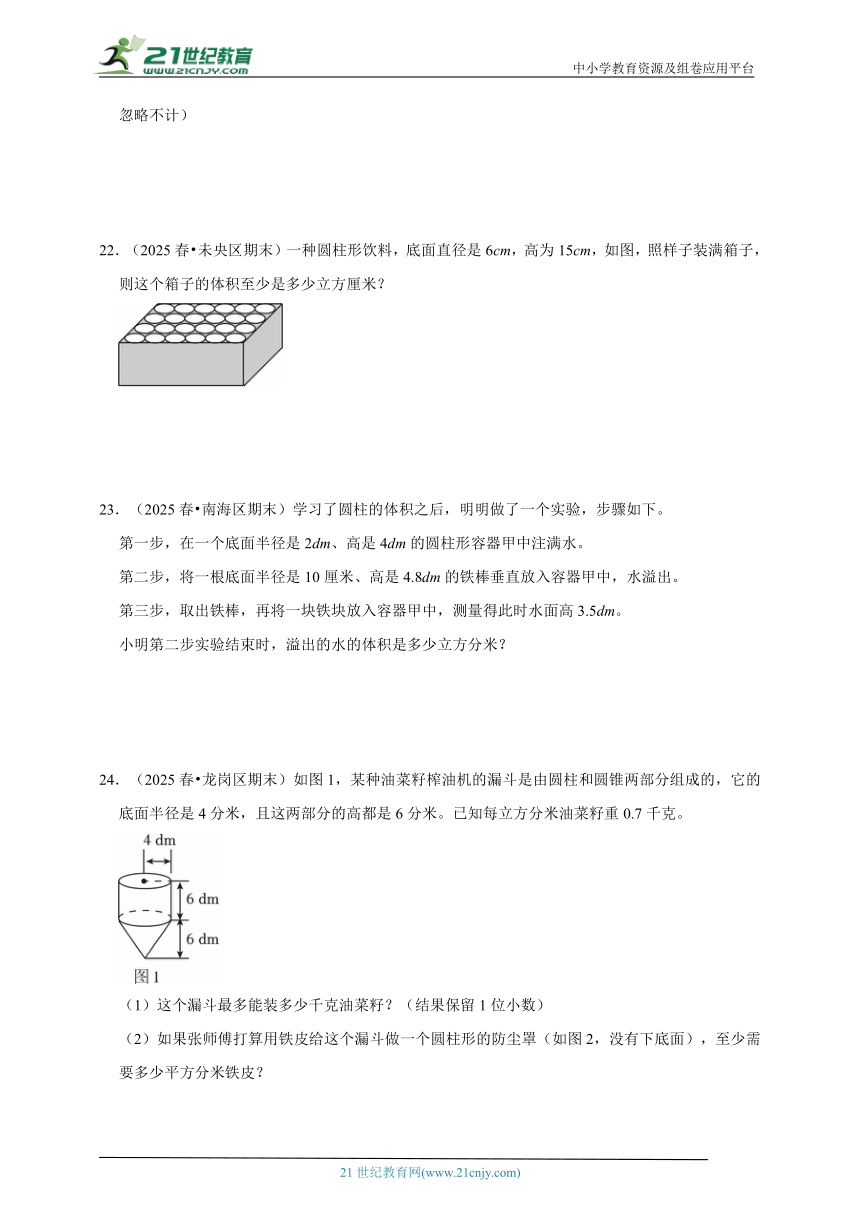
2.(2025春 福田区期末)某工厂生产了一种饮料桶,尺寸如图所示(单位:厘米)。下面有三种饮料桶侧面的商标纸,你认为哪种纸与饮料桶侧面积最接近?( )
A. B.
C. D.以上都可以
3.(2025春 城阳区期末)如图所示,把直径和高都是6厘米的圆柱平均切成若干等份,拼成一个近似的长方体。下面的选项中,描述正确的是( )
①体积不变,表面积增加了36平方厘米。
②圆柱侧面积是56.52平方厘米。
③长方体体积是169.56立方厘米。
A.①② B.②③ C.①③
4.(2025春 莲湖区期末)下面的圆柱( )与左边的圆锥体积相等。
A. B.
C. D.
5.(2025春 莲湖区期末)如图,把一个体积是48立方分米的圆柱形木块,削成两个相同的圆锥形木块,则一个圆锥形木块的体积是( )立方分米。
A.8 B.16 C.10 D.24
6.(2025春 南海区期末)有两张长6cm、宽5cm的长方形纸片,一张用长作高围成甲圆柱,另一张用宽作高围成乙圆柱,围成的圆柱侧面积相比,( )
A.侧面积一样大
B.甲圆柱的侧面积大
C.乙圆柱的侧面积大
D.无法确定哪个圆柱的侧面积大
7.(2025春 忠县期末)用两根完全相同的圆柱形木料分别做成如图中甲、乙两个模型(图中阴影部分),甲和乙的体积相比,( )
A.甲的体积大 B.乙的体积大
C.甲和乙的体积相等 D.无法比较
8.(2025春 寿光市期末)冰球运动是以冰刀和冰球杆为工具,在冰上进行的一种集体性竞技运动,冰球是用硬橡胶制成的圆柱体,厚为2.54厘米、底面直径为7.62厘米,质量为156克~170克。将3个冰球重叠在一起,表面积比原来减少了( )平方厘米。
A.3.14×(7.62÷2)2×6 B.3.14×7.622×4
C.3.14×(7.62÷2)2×4 D.3.14×7.622×6
二.填空题(共8小题)
9.(2025春 碑林区期末)为实现《中国制造2025》西安市举办3D打印博览会,将用60立方分米材料,打印等底等高的圆柱和圆锥各一个,材料没有剩余和浪费,圆柱的体积是 立方分米,圆锥是体积是 立方分米。
10.(2025春 临平区期末)图中三角形与长方形的面积比是 : ;如果两个图形分别绕6厘米的边为轴旋转一周,形成的圆锥的体积与圆柱的体积比是 : 。
11.(2025春 法库县期末)一个圆柱与圆锥底面周长相等、高也相等。圆锥的体积是2.4立方分米,圆柱体积是 立方分米。
12.(2025春 碑林区期末)把一根圆柱形木料沿截面截去3厘米,表面积减少18.84平方厘米,那么,截去部分的体积是 立方厘米。
13.(2025春 碑林区期末)将一个高3dm的圆柱,沿底面直径竖直切成相同的两部分,表面积增加12dm2,这个圆柱原来的侧面积是 dm2,一个底面面积是 dm2。
14.(2025春 长清区期末)阿基米德是历史上杰出的数学家之一,在他众多的科学发现中他自己最为满意的是“圆柱容球”定理。如图,把一个球放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,图中球的体积是 cm3。(π取3.14)
15.(2025春 龙华区期末)请你制作一个无盖圆柱形水桶,有如图中四种型号的铁皮可以搭配选择。
(1)你选择的材料是 号和 号。
(2)用你选择的材料制作的水桶的容积是 立方分米。
16.(2025春 白云区期末)一个圆锥底面周长是6.28cm,高是9cm,它的体积是 cm3。一个与它底面积、高分别相等的圆柱,体积是 cm3。
三.计算题(共3小题)
17.(2025春 高陵区期末)计算下面图形的体积。
18.(2024春 丹江口市期末)求如图这个零件的体积。(单位:cm)
19.(2024春 龙里县期末)求下面图形的表面积和体积。
四.应用题(共6小题)
20.(2025春 碑林区期末)如图是一块长方形铁皮,利用图中的阴影部分,可做一个圆柱形铁桶,(接缝和厚度忽略不计)这个油桶的容积是多少?
21.(2025春 西安期末)一个底面直径为20cm的圆柱形玻璃杯中装有一部分水,水深10cm,将一个底面直径4cm、高6cm的圆锥体没入水中,水没有溢出,求水面上升了多少厘米?(容器厚度忽略不计)
22.(2025春 未央区期末)一种圆柱形饮料,底面直径是6cm,高为15cm,如图,照样子装满箱子,则这个箱子的体积至少是多少立方厘米?
23.(2025春 南海区期末)学习了圆柱的体积之后,明明做了一个实验,步骤如下。
第一步,在一个底面半径是2dm、高是4dm的圆柱形容器甲中注满水。
第二步,将一根底面半径是10厘米、高是4.8dm的铁棒垂直放入容器甲中,水溢出。
第三步,取出铁棒,再将一块铁块放入容器甲中,测量得此时水面高3.5dm。
小明第二步实验结束时,溢出的水的体积是多少立方分米?
24.(2025春 龙岗区期末)如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的,它的底面半径是4分米,且这两部分的高都是6分米。已知每立方分米油菜籽重0.7千克。
(1)这个漏斗最多能装多少千克油菜籽?(结果保留1位小数)
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
25.(2025春 裕华区期末)竹节人,也称竹人,是我国一种传统的手工艺品。它是由空心竹子制成的小型人形雕像。竹节人的身体由1截较长的竹子和8截较短的竹子组成,制作方法及数据如图。这个竹节人的体积是多少立方厘米?(π取3)(单位:厘米)
【小升初真题汇编】查漏补缺专题09圆柱与圆锥-2025年小学数学通用版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C C C A A C C
一.选择题(共8小题)
1.(2025春 济南校级期末)把一个底面积为3.14cm2、高为10cm的圆柱形橡皮泥捏成一个底面积为12.56cm2的圆柱,高变为( )cm。
A.20 B.10 C.5 D.2.5
【解答】解:3.14×10÷12.56
=31.4÷12.56
=2.5(cm)
答:高变为2.5cm。
故选:D。
2.(2025春 福田区期末)某工厂生产了一种饮料桶,尺寸如图所示(单位:厘米)。下面有三种饮料桶侧面的商标纸,你认为哪种纸与饮料桶侧面积最接近?( )
A. B.
C. D.以上都可以
【解答】解:饮料桶的侧面积是:3.14×8×12=301.44(平方厘米),
对于A,商标纸的面积是:30×12=360(平方厘米),
对于B,商标纸的面积是:8×12=96(平方厘米),
对于C,商标纸的面积是:26×12=312(平方厘米),
比较可得最接近饮料桶侧面积的商标纸的面积是312平方厘米。
故选:C。
3.(2025春 城阳区期末)如图所示,把直径和高都是6厘米的圆柱平均切成若干等份,拼成一个近似的长方体。下面的选项中,描述正确的是( )
①体积不变,表面积增加了36平方厘米。
②圆柱侧面积是56.52平方厘米。
③长方体体积是169.56立方厘米。
A.①② B.②③ C.①③
【解答】解:6÷2=3(厘米),
长方体和圆柱的体积均是:
3.14×32×6
=3.14×54
=169.56(平方厘米)
长方形的长是:3.14×6÷2=9.42(厘米)
长方体的表面积是:(9.42×3+3×6+6×9.42)×2=205.56(平方厘米),
圆柱的侧面积是:3.14×6×6=113.04(平方厘米)
圆柱的表面积是:113.04+3.14×32×2=169.56(平方厘米),
205.56﹣169.56=36(平方厘米)。
故①③正确,②错误。
故选:C。
4.(2025春 莲湖区期末)下面的圆柱( )与左边的圆锥体积相等。
A. B.
C. D.
【解答】解:圆锥体积:
3.14×(6÷2)2×9÷3=84.78(立方厘米)
A.圆柱体积:3.14×(6÷2)2×9=254.34(立方厘米)
B.圆柱体积:3.14×(2÷2)2×9=28.26(立方厘米)
C.圆柱体积:3.14×(6÷2)2×3=84.78(立方厘米)
D.圆柱体积:3.14×(2÷2)2×3=9.42(立方厘米)
与圆锥体积相等的圆柱为C选项的图形。
故选:C。
5.(2025春 莲湖区期末)如图,把一个体积是48立方分米的圆柱形木块,削成两个相同的圆锥形木块,则一个圆锥形木块的体积是( )立方分米。
A.8 B.16 C.10 D.24
【解答】解:48÷2
=24
=8(立方分米)
答:一个圆锥形木块的体积是8立方分米。
故选:A。
6.(2025春 南海区期末)有两张长6cm、宽5cm的长方形纸片,一张用长作高围成甲圆柱,另一张用宽作高围成乙圆柱,围成的圆柱侧面积相比,( )
A.侧面积一样大
B.甲圆柱的侧面积大
C.乙圆柱的侧面积大
D.无法确定哪个圆柱的侧面积大
【解答】解:圆柱侧面积=6×5=30(cm2)
答:两种围法围成的圆柱侧面积一样大。
故选:A。
7.(2025春 忠县期末)用两根完全相同的圆柱形木料分别做成如图中甲、乙两个模型(图中阴影部分),甲和乙的体积相比,( )
A.甲的体积大 B.乙的体积大
C.甲和乙的体积相等 D.无法比较
【解答】解:底面积相同时,两个高为a的圆锥的体积之和,等于一个高为a的圆锥的体积;已知原来两个圆柱的体积相等,而空白处的图形的体积也相等,所以涂色部分的体积也相等。
故选:C。
8.(2025春 寿光市期末)冰球运动是以冰刀和冰球杆为工具,在冰上进行的一种集体性竞技运动,冰球是用硬橡胶制成的圆柱体,厚为2.54厘米、底面直径为7.62厘米,质量为156克~170克。将3个冰球重叠在一起,表面积比原来减少了( )平方厘米。
A.3.14×(7.62÷2)2×6 B.3.14×7.622×4
C.3.14×(7.62÷2)2×4 D.3.14×7.622×6
【解答】解:将3个冰球重叠在一起,表面积比原来减少了多少平方厘米,列式是:3.14×(7.62÷2)2×4。
故选:C。
二.填空题(共8小题)
9.(2025春 碑林区期末)为实现《中国制造2025》西安市举办3D打印博览会,将用60立方分米材料,打印等底等高的圆柱和圆锥各一个,材料没有剩余和浪费,圆柱的体积是 45 立方分米,圆锥是体积是 15 立方分米。
【解答】解:60÷(1+3)
=60÷4
=15(立方分米)
15×3=45(立方分米)
答:圆柱的体积是45立方分米,圆锥的体积是15立方分米。
故答案为:45;15。
10.(2025春 临平区期末)图中三角形与长方形的面积比是 1 : 2 ;如果两个图形分别绕6厘米的边为轴旋转一周,形成的圆锥的体积与圆柱的体积比是 1 : 3 。
【解答】解:三角形和长方形的等底等高,则三角形的面积是长方形面积的,即图中三角形与长方形的面积比是1:2;
因为圆锥与圆柱等底等高,则圆锥的体积是圆柱体积的,即如果两个图形分别绕6厘米的边为轴旋转一周,形成的圆锥的体积与圆柱的体积比是1:3。
故答案为:1,2;1,3。
11.(2025春 法库县期末)一个圆柱与圆锥底面周长相等、高也相等。圆锥的体积是2.4立方分米,圆柱体积是 7.2 立方分米。
【解答】解:2.4×3=7.2(立方分米)
答:圆柱体积是7.2立方分米。
故答案为:7.2。
12.(2025春 碑林区期末)把一根圆柱形木料沿截面截去3厘米,表面积减少18.84平方厘米,那么,截去部分的体积是 9.42 立方厘米。
【解答】解:18.84÷3=6.28(厘米)
6.28÷2π=1(厘米)
3.14×12×3
=3.14×3
=9.42(立方厘米)
答:截去部分的体积是9.42立方厘米。
故答案为:9.42。
13.(2025春 碑林区期末)将一个高3dm的圆柱,沿底面直径竖直切成相同的两部分,表面积增加12dm2,这个圆柱原来的侧面积是 18.84 dm2,一个底面面积是 3.14 dm2。
【解答】解:12÷2÷3
=6÷3
=2(dm)
2π×3
=6π
=6×3.14
=18.84(dm2)
2÷2=1(dm)
π×12=3.14(dm2)
答:这个圆柱原来的侧面积是18.84dm2,一个底面面积是3.14dm2。
故答案为:18.84;3.14。
14.(2025春 长清区期末)阿基米德是历史上杰出的数学家之一,在他众多的科学发现中他自己最为满意的是“圆柱容球”定理。如图,把一个球放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,图中球的体积是 904.32 cm3。(π取3.14)
【解答】解:3.14×(12÷2)2×12
=3.14×36×8
=904.32(立方厘米)
答:球的体积是904.32cm3。
故答案为:904.32。
15.(2025春 龙华区期末)请你制作一个无盖圆柱形水桶,有如图中四种型号的铁皮可以搭配选择。
(1)你选择的材料是 ① 号和 ④ 号。
(2)用你选择的材料制作的水桶的容积是 14.13 立方分米。
【解答】解:(1)根据分析选择的材料是①号和④号(答案不唯一)。
(2)3.14×(3÷2)2×2
=3.14×1.52×2
=3.14×2.25×2
=7.065×2
=14.13(立方分米)
故答案为:(1)①;④(答案不唯一);(2)14.13。
16.(2025春 白云区期末)一个圆锥底面周长是6.28cm,高是9cm,它的体积是 9.42 cm3。一个与它底面积、高分别相等的圆柱,体积是 28.26 cm3。
【解答】解:6.28÷3.14÷2=1(厘米)
3.14×1×1×9÷3=9.42(立方厘米)
9.42×3=28.26(立方厘米)
答:圆锥的体积是9.42立方厘米;圆柱的体积是28.26立方厘米。
故答案为:9.42;28.26。
三.计算题(共3小题)
17.(2025春 高陵区期末)计算下面图形的体积。
【解答】解:(1)3.14×62×10
=3.14×36×10
=113.04×10
=1130.4(cm3)
(2)3.14×(16÷2)2×21
3.14×82×21
3.14×64×21
21×3.14×64
=7×3.14×64
=21.98×64
=1406.72(cm3)
18.(2024春 丹江口市期末)求如图这个零件的体积。(单位:cm)
【解答】解:20×30×15﹣3.14×52×30÷2
=9000﹣1177.5
=7822.5(cm3)
答:图形的体积是7822.5cm3。
19.(2024春 龙里县期末)求下面图形的表面积和体积。
【解答】解:表面积:3.14×(14÷2)2×2+3.14×14×4+3.14×4×4
=3.14×49×2+3.14×14×4+3.14×4×4
=3.14×(49×2+14×4+4×4)
=3.14×(98+56+16)
=3.14×170
=533.8(平方厘米)
体积:3.14×(14÷2)2×4+3.14×(4÷2)2×4
=3.14×49×4+3.14×4×4
=3.14×(49×4+4×4)
=3.14×(196+16)
=3.14×212
=665.68(立方厘米)
四.应用题(共6小题)
20.(2025春 碑林区期末)如图是一块长方形铁皮,利用图中的阴影部分,可做一个圆柱形铁桶,(接缝和厚度忽略不计)这个油桶的容积是多少?
【解答】解:3.14×(4÷2÷2)2×4
=3.14×1×4
=3.14×4
=12.56(立方分米)
12.56立方分米=12.56升
答:这个油桶的容积是12.56升。
21.(2025春 西安期末)一个底面直径为20cm的圆柱形玻璃杯中装有一部分水,水深10cm,将一个底面直径4cm、高6cm的圆锥体没入水中,水没有溢出,求水面上升了多少厘米?(容器厚度忽略不计)
【解答】解:3.14×(20÷2)2
=3.14×102
=3.14×100
=314(平方厘米)
3.14×(4÷2)2×6
=3.14×22×6
=3.14×4×6
=12.56×(6)
=12.56×2
=25.12(立方厘米)
25.12÷314=0.08(厘米)
答:水面上升了0.8厘米。
22.(2025春 未央区期末)一种圆柱形饮料,底面直径是6cm,高为15cm,如图,照样子装满箱子,则这个箱子的体积至少是多少立方厘米?
【解答】解:(6×6)×(6×4)×15
=36×24×15
=12960(cm3)
答:这个箱子的体积至少是12960立方厘米。
23.(2025春 南海区期末)学习了圆柱的体积之后,明明做了一个实验,步骤如下。
第一步,在一个底面半径是2dm、高是4dm的圆柱形容器甲中注满水。
第二步,将一根底面半径是10厘米、高是4.8dm的铁棒垂直放入容器甲中,水溢出。
第三步,取出铁棒,再将一块铁块放入容器甲中,测量得此时水面高3.5dm。
小明第二步实验结束时,溢出的水的体积是多少立方分米?
【解答】解:10厘米=1分米
3.14×12×4
=3.14×4
=12.56(立方分米)
答:溢出的水的体积是12.56立方分米。
24.(2025春 龙岗区期末)如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的,它的底面半径是4分米,且这两部分的高都是6分米。已知每立方分米油菜籽重0.7千克。
(1)这个漏斗最多能装多少千克油菜籽?(结果保留1位小数)
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
【解答】解:油菜籽的体积:
(1)3.14×42×6+3.14×42×6÷3
=3.14×16×6+3.14×16×6÷3
=50.24×6+50.24×6÷3
=301.44+301.44÷3
=301.44+100.48
=401.92(dm3)
油菜籽的质量:
0.7×401.92≈281.3(千克)
答:这个漏斗最多能装281.3千克油菜籽。
(2)3.14×10×12+3.14×(10÷2)2
=31.4×12+3.14×52
=376.8+3.14×25
=376.8+78.5
=455.3(dm2)
答:做这个防尘罩至少需要455.3平方分米铁皮。
25.(2025春 裕华区期末)竹节人,也称竹人,是我国一种传统的手工艺品。它是由空心竹子制成的小型人形雕像。竹节人的身体由1截较长的竹子和8截较短的竹子组成,制作方法及数据如图。这个竹节人的体积是多少立方厘米?(π取3)(单位:厘米)
【解答】解:底面半径:1.2÷2=0.6(厘米),1÷2=0.5(厘米)
一节较长竹子的体积:(3×0.6×0.6﹣3×0.5×0.5)×6=1.98(立方厘米),
一节较短竹子的体积:(3×0.6×0.6﹣3×0.5×0.5)×2=0.66(立方厘米),
1.98+0.66×8
=1.98+5.28
=7.26(立方厘米)
答:这个竹节人的体积是7.26立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【小升初真题汇编】查漏补缺专题09圆柱与圆锥-2025年小学数学通用版
一.选择题(共8小题)
1.(2025春 济南校级期末)把一个底面积为3.14cm2、高为10cm的圆柱形橡皮泥捏成一个底面积为12.56cm2的圆柱,高变为( )cm。
A.20 B.10 C.5 D.2.5
2.(2025春 福田区期末)某工厂生产了一种饮料桶,尺寸如图所示(单位:厘米)。下面有三种饮料桶侧面的商标纸,你认为哪种纸与饮料桶侧面积最接近?( )
A. B.
C. D.以上都可以
3.(2025春 城阳区期末)如图所示,把直径和高都是6厘米的圆柱平均切成若干等份,拼成一个近似的长方体。下面的选项中,描述正确的是( )
①体积不变,表面积增加了36平方厘米。
②圆柱侧面积是56.52平方厘米。
③长方体体积是169.56立方厘米。
A.①② B.②③ C.①③
4.(2025春 莲湖区期末)下面的圆柱( )与左边的圆锥体积相等。
A. B.
C. D.
5.(2025春 莲湖区期末)如图,把一个体积是48立方分米的圆柱形木块,削成两个相同的圆锥形木块,则一个圆锥形木块的体积是( )立方分米。
A.8 B.16 C.10 D.24
6.(2025春 南海区期末)有两张长6cm、宽5cm的长方形纸片,一张用长作高围成甲圆柱,另一张用宽作高围成乙圆柱,围成的圆柱侧面积相比,( )
A.侧面积一样大
B.甲圆柱的侧面积大
C.乙圆柱的侧面积大
D.无法确定哪个圆柱的侧面积大
7.(2025春 忠县期末)用两根完全相同的圆柱形木料分别做成如图中甲、乙两个模型(图中阴影部分),甲和乙的体积相比,( )
A.甲的体积大 B.乙的体积大
C.甲和乙的体积相等 D.无法比较
8.(2025春 寿光市期末)冰球运动是以冰刀和冰球杆为工具,在冰上进行的一种集体性竞技运动,冰球是用硬橡胶制成的圆柱体,厚为2.54厘米、底面直径为7.62厘米,质量为156克~170克。将3个冰球重叠在一起,表面积比原来减少了( )平方厘米。
A.3.14×(7.62÷2)2×6 B.3.14×7.622×4
C.3.14×(7.62÷2)2×4 D.3.14×7.622×6
二.填空题(共8小题)
9.(2025春 碑林区期末)为实现《中国制造2025》西安市举办3D打印博览会,将用60立方分米材料,打印等底等高的圆柱和圆锥各一个,材料没有剩余和浪费,圆柱的体积是 立方分米,圆锥是体积是 立方分米。
10.(2025春 临平区期末)图中三角形与长方形的面积比是 : ;如果两个图形分别绕6厘米的边为轴旋转一周,形成的圆锥的体积与圆柱的体积比是 : 。
11.(2025春 法库县期末)一个圆柱与圆锥底面周长相等、高也相等。圆锥的体积是2.4立方分米,圆柱体积是 立方分米。
12.(2025春 碑林区期末)把一根圆柱形木料沿截面截去3厘米,表面积减少18.84平方厘米,那么,截去部分的体积是 立方厘米。
13.(2025春 碑林区期末)将一个高3dm的圆柱,沿底面直径竖直切成相同的两部分,表面积增加12dm2,这个圆柱原来的侧面积是 dm2,一个底面面积是 dm2。
14.(2025春 长清区期末)阿基米德是历史上杰出的数学家之一,在他众多的科学发现中他自己最为满意的是“圆柱容球”定理。如图,把一个球放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,图中球的体积是 cm3。(π取3.14)
15.(2025春 龙华区期末)请你制作一个无盖圆柱形水桶,有如图中四种型号的铁皮可以搭配选择。
(1)你选择的材料是 号和 号。
(2)用你选择的材料制作的水桶的容积是 立方分米。
16.(2025春 白云区期末)一个圆锥底面周长是6.28cm,高是9cm,它的体积是 cm3。一个与它底面积、高分别相等的圆柱,体积是 cm3。
三.计算题(共3小题)
17.(2025春 高陵区期末)计算下面图形的体积。
18.(2024春 丹江口市期末)求如图这个零件的体积。(单位:cm)
19.(2024春 龙里县期末)求下面图形的表面积和体积。
四.应用题(共6小题)
20.(2025春 碑林区期末)如图是一块长方形铁皮,利用图中的阴影部分,可做一个圆柱形铁桶,(接缝和厚度忽略不计)这个油桶的容积是多少?
21.(2025春 西安期末)一个底面直径为20cm的圆柱形玻璃杯中装有一部分水,水深10cm,将一个底面直径4cm、高6cm的圆锥体没入水中,水没有溢出,求水面上升了多少厘米?(容器厚度忽略不计)
22.(2025春 未央区期末)一种圆柱形饮料,底面直径是6cm,高为15cm,如图,照样子装满箱子,则这个箱子的体积至少是多少立方厘米?
23.(2025春 南海区期末)学习了圆柱的体积之后,明明做了一个实验,步骤如下。
第一步,在一个底面半径是2dm、高是4dm的圆柱形容器甲中注满水。
第二步,将一根底面半径是10厘米、高是4.8dm的铁棒垂直放入容器甲中,水溢出。
第三步,取出铁棒,再将一块铁块放入容器甲中,测量得此时水面高3.5dm。
小明第二步实验结束时,溢出的水的体积是多少立方分米?
24.(2025春 龙岗区期末)如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的,它的底面半径是4分米,且这两部分的高都是6分米。已知每立方分米油菜籽重0.7千克。
(1)这个漏斗最多能装多少千克油菜籽?(结果保留1位小数)
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
25.(2025春 裕华区期末)竹节人,也称竹人,是我国一种传统的手工艺品。它是由空心竹子制成的小型人形雕像。竹节人的身体由1截较长的竹子和8截较短的竹子组成,制作方法及数据如图。这个竹节人的体积是多少立方厘米?(π取3)(单位:厘米)
【小升初真题汇编】查漏补缺专题09圆柱与圆锥-2025年小学数学通用版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C C C A A C C
一.选择题(共8小题)
1.(2025春 济南校级期末)把一个底面积为3.14cm2、高为10cm的圆柱形橡皮泥捏成一个底面积为12.56cm2的圆柱,高变为( )cm。
A.20 B.10 C.5 D.2.5
【解答】解:3.14×10÷12.56
=31.4÷12.56
=2.5(cm)
答:高变为2.5cm。
故选:D。
2.(2025春 福田区期末)某工厂生产了一种饮料桶,尺寸如图所示(单位:厘米)。下面有三种饮料桶侧面的商标纸,你认为哪种纸与饮料桶侧面积最接近?( )
A. B.
C. D.以上都可以
【解答】解:饮料桶的侧面积是:3.14×8×12=301.44(平方厘米),
对于A,商标纸的面积是:30×12=360(平方厘米),
对于B,商标纸的面积是:8×12=96(平方厘米),
对于C,商标纸的面积是:26×12=312(平方厘米),
比较可得最接近饮料桶侧面积的商标纸的面积是312平方厘米。
故选:C。
3.(2025春 城阳区期末)如图所示,把直径和高都是6厘米的圆柱平均切成若干等份,拼成一个近似的长方体。下面的选项中,描述正确的是( )
①体积不变,表面积增加了36平方厘米。
②圆柱侧面积是56.52平方厘米。
③长方体体积是169.56立方厘米。
A.①② B.②③ C.①③
【解答】解:6÷2=3(厘米),
长方体和圆柱的体积均是:
3.14×32×6
=3.14×54
=169.56(平方厘米)
长方形的长是:3.14×6÷2=9.42(厘米)
长方体的表面积是:(9.42×3+3×6+6×9.42)×2=205.56(平方厘米),
圆柱的侧面积是:3.14×6×6=113.04(平方厘米)
圆柱的表面积是:113.04+3.14×32×2=169.56(平方厘米),
205.56﹣169.56=36(平方厘米)。
故①③正确,②错误。
故选:C。
4.(2025春 莲湖区期末)下面的圆柱( )与左边的圆锥体积相等。
A. B.
C. D.
【解答】解:圆锥体积:
3.14×(6÷2)2×9÷3=84.78(立方厘米)
A.圆柱体积:3.14×(6÷2)2×9=254.34(立方厘米)
B.圆柱体积:3.14×(2÷2)2×9=28.26(立方厘米)
C.圆柱体积:3.14×(6÷2)2×3=84.78(立方厘米)
D.圆柱体积:3.14×(2÷2)2×3=9.42(立方厘米)
与圆锥体积相等的圆柱为C选项的图形。
故选:C。
5.(2025春 莲湖区期末)如图,把一个体积是48立方分米的圆柱形木块,削成两个相同的圆锥形木块,则一个圆锥形木块的体积是( )立方分米。
A.8 B.16 C.10 D.24
【解答】解:48÷2
=24
=8(立方分米)
答:一个圆锥形木块的体积是8立方分米。
故选:A。
6.(2025春 南海区期末)有两张长6cm、宽5cm的长方形纸片,一张用长作高围成甲圆柱,另一张用宽作高围成乙圆柱,围成的圆柱侧面积相比,( )
A.侧面积一样大
B.甲圆柱的侧面积大
C.乙圆柱的侧面积大
D.无法确定哪个圆柱的侧面积大
【解答】解:圆柱侧面积=6×5=30(cm2)
答:两种围法围成的圆柱侧面积一样大。
故选:A。
7.(2025春 忠县期末)用两根完全相同的圆柱形木料分别做成如图中甲、乙两个模型(图中阴影部分),甲和乙的体积相比,( )
A.甲的体积大 B.乙的体积大
C.甲和乙的体积相等 D.无法比较
【解答】解:底面积相同时,两个高为a的圆锥的体积之和,等于一个高为a的圆锥的体积;已知原来两个圆柱的体积相等,而空白处的图形的体积也相等,所以涂色部分的体积也相等。
故选:C。
8.(2025春 寿光市期末)冰球运动是以冰刀和冰球杆为工具,在冰上进行的一种集体性竞技运动,冰球是用硬橡胶制成的圆柱体,厚为2.54厘米、底面直径为7.62厘米,质量为156克~170克。将3个冰球重叠在一起,表面积比原来减少了( )平方厘米。
A.3.14×(7.62÷2)2×6 B.3.14×7.622×4
C.3.14×(7.62÷2)2×4 D.3.14×7.622×6
【解答】解:将3个冰球重叠在一起,表面积比原来减少了多少平方厘米,列式是:3.14×(7.62÷2)2×4。
故选:C。
二.填空题(共8小题)
9.(2025春 碑林区期末)为实现《中国制造2025》西安市举办3D打印博览会,将用60立方分米材料,打印等底等高的圆柱和圆锥各一个,材料没有剩余和浪费,圆柱的体积是 45 立方分米,圆锥是体积是 15 立方分米。
【解答】解:60÷(1+3)
=60÷4
=15(立方分米)
15×3=45(立方分米)
答:圆柱的体积是45立方分米,圆锥的体积是15立方分米。
故答案为:45;15。
10.(2025春 临平区期末)图中三角形与长方形的面积比是 1 : 2 ;如果两个图形分别绕6厘米的边为轴旋转一周,形成的圆锥的体积与圆柱的体积比是 1 : 3 。
【解答】解:三角形和长方形的等底等高,则三角形的面积是长方形面积的,即图中三角形与长方形的面积比是1:2;
因为圆锥与圆柱等底等高,则圆锥的体积是圆柱体积的,即如果两个图形分别绕6厘米的边为轴旋转一周,形成的圆锥的体积与圆柱的体积比是1:3。
故答案为:1,2;1,3。
11.(2025春 法库县期末)一个圆柱与圆锥底面周长相等、高也相等。圆锥的体积是2.4立方分米,圆柱体积是 7.2 立方分米。
【解答】解:2.4×3=7.2(立方分米)
答:圆柱体积是7.2立方分米。
故答案为:7.2。
12.(2025春 碑林区期末)把一根圆柱形木料沿截面截去3厘米,表面积减少18.84平方厘米,那么,截去部分的体积是 9.42 立方厘米。
【解答】解:18.84÷3=6.28(厘米)
6.28÷2π=1(厘米)
3.14×12×3
=3.14×3
=9.42(立方厘米)
答:截去部分的体积是9.42立方厘米。
故答案为:9.42。
13.(2025春 碑林区期末)将一个高3dm的圆柱,沿底面直径竖直切成相同的两部分,表面积增加12dm2,这个圆柱原来的侧面积是 18.84 dm2,一个底面面积是 3.14 dm2。
【解答】解:12÷2÷3
=6÷3
=2(dm)
2π×3
=6π
=6×3.14
=18.84(dm2)
2÷2=1(dm)
π×12=3.14(dm2)
答:这个圆柱原来的侧面积是18.84dm2,一个底面面积是3.14dm2。
故答案为:18.84;3.14。
14.(2025春 长清区期末)阿基米德是历史上杰出的数学家之一,在他众多的科学发现中他自己最为满意的是“圆柱容球”定理。如图,把一个球放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,图中球的体积是 904.32 cm3。(π取3.14)
【解答】解:3.14×(12÷2)2×12
=3.14×36×8
=904.32(立方厘米)
答:球的体积是904.32cm3。
故答案为:904.32。
15.(2025春 龙华区期末)请你制作一个无盖圆柱形水桶,有如图中四种型号的铁皮可以搭配选择。
(1)你选择的材料是 ① 号和 ④ 号。
(2)用你选择的材料制作的水桶的容积是 14.13 立方分米。
【解答】解:(1)根据分析选择的材料是①号和④号(答案不唯一)。
(2)3.14×(3÷2)2×2
=3.14×1.52×2
=3.14×2.25×2
=7.065×2
=14.13(立方分米)
故答案为:(1)①;④(答案不唯一);(2)14.13。
16.(2025春 白云区期末)一个圆锥底面周长是6.28cm,高是9cm,它的体积是 9.42 cm3。一个与它底面积、高分别相等的圆柱,体积是 28.26 cm3。
【解答】解:6.28÷3.14÷2=1(厘米)
3.14×1×1×9÷3=9.42(立方厘米)
9.42×3=28.26(立方厘米)
答:圆锥的体积是9.42立方厘米;圆柱的体积是28.26立方厘米。
故答案为:9.42;28.26。
三.计算题(共3小题)
17.(2025春 高陵区期末)计算下面图形的体积。
【解答】解:(1)3.14×62×10
=3.14×36×10
=113.04×10
=1130.4(cm3)
(2)3.14×(16÷2)2×21
3.14×82×21
3.14×64×21
21×3.14×64
=7×3.14×64
=21.98×64
=1406.72(cm3)
18.(2024春 丹江口市期末)求如图这个零件的体积。(单位:cm)
【解答】解:20×30×15﹣3.14×52×30÷2
=9000﹣1177.5
=7822.5(cm3)
答:图形的体积是7822.5cm3。
19.(2024春 龙里县期末)求下面图形的表面积和体积。
【解答】解:表面积:3.14×(14÷2)2×2+3.14×14×4+3.14×4×4
=3.14×49×2+3.14×14×4+3.14×4×4
=3.14×(49×2+14×4+4×4)
=3.14×(98+56+16)
=3.14×170
=533.8(平方厘米)
体积:3.14×(14÷2)2×4+3.14×(4÷2)2×4
=3.14×49×4+3.14×4×4
=3.14×(49×4+4×4)
=3.14×(196+16)
=3.14×212
=665.68(立方厘米)
四.应用题(共6小题)
20.(2025春 碑林区期末)如图是一块长方形铁皮,利用图中的阴影部分,可做一个圆柱形铁桶,(接缝和厚度忽略不计)这个油桶的容积是多少?
【解答】解:3.14×(4÷2÷2)2×4
=3.14×1×4
=3.14×4
=12.56(立方分米)
12.56立方分米=12.56升
答:这个油桶的容积是12.56升。
21.(2025春 西安期末)一个底面直径为20cm的圆柱形玻璃杯中装有一部分水,水深10cm,将一个底面直径4cm、高6cm的圆锥体没入水中,水没有溢出,求水面上升了多少厘米?(容器厚度忽略不计)
【解答】解:3.14×(20÷2)2
=3.14×102
=3.14×100
=314(平方厘米)
3.14×(4÷2)2×6
=3.14×22×6
=3.14×4×6
=12.56×(6)
=12.56×2
=25.12(立方厘米)
25.12÷314=0.08(厘米)
答:水面上升了0.8厘米。
22.(2025春 未央区期末)一种圆柱形饮料,底面直径是6cm,高为15cm,如图,照样子装满箱子,则这个箱子的体积至少是多少立方厘米?
【解答】解:(6×6)×(6×4)×15
=36×24×15
=12960(cm3)
答:这个箱子的体积至少是12960立方厘米。
23.(2025春 南海区期末)学习了圆柱的体积之后,明明做了一个实验,步骤如下。
第一步,在一个底面半径是2dm、高是4dm的圆柱形容器甲中注满水。
第二步,将一根底面半径是10厘米、高是4.8dm的铁棒垂直放入容器甲中,水溢出。
第三步,取出铁棒,再将一块铁块放入容器甲中,测量得此时水面高3.5dm。
小明第二步实验结束时,溢出的水的体积是多少立方分米?
【解答】解:10厘米=1分米
3.14×12×4
=3.14×4
=12.56(立方分米)
答:溢出的水的体积是12.56立方分米。
24.(2025春 龙岗区期末)如图1,某种油菜籽榨油机的漏斗是由圆柱和圆锥两部分组成的,它的底面半径是4分米,且这两部分的高都是6分米。已知每立方分米油菜籽重0.7千克。
(1)这个漏斗最多能装多少千克油菜籽?(结果保留1位小数)
(2)如果张师傅打算用铁皮给这个漏斗做一个圆柱形的防尘罩(如图2,没有下底面),至少需要多少平方分米铁皮?
【解答】解:油菜籽的体积:
(1)3.14×42×6+3.14×42×6÷3
=3.14×16×6+3.14×16×6÷3
=50.24×6+50.24×6÷3
=301.44+301.44÷3
=301.44+100.48
=401.92(dm3)
油菜籽的质量:
0.7×401.92≈281.3(千克)
答:这个漏斗最多能装281.3千克油菜籽。
(2)3.14×10×12+3.14×(10÷2)2
=31.4×12+3.14×52
=376.8+3.14×25
=376.8+78.5
=455.3(dm2)
答:做这个防尘罩至少需要455.3平方分米铁皮。
25.(2025春 裕华区期末)竹节人,也称竹人,是我国一种传统的手工艺品。它是由空心竹子制成的小型人形雕像。竹节人的身体由1截较长的竹子和8截较短的竹子组成,制作方法及数据如图。这个竹节人的体积是多少立方厘米?(π取3)(单位:厘米)
【解答】解:底面半径:1.2÷2=0.6(厘米),1÷2=0.5(厘米)
一节较长竹子的体积:(3×0.6×0.6﹣3×0.5×0.5)×6=1.98(立方厘米),
一节较短竹子的体积:(3×0.6×0.6﹣3×0.5×0.5)×2=0.66(立方厘米),
1.98+0.66×8
=1.98+5.28
=7.26(立方厘米)
答:这个竹节人的体积是7.26立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
