13.1.3 三角形中几条重要线段 课件(共29张PPT) 2025-2026学年沪科版八年级数学上册
文档属性
| 名称 | 13.1.3 三角形中几条重要线段 课件(共29张PPT) 2025-2026学年沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 13:29:33 | ||
图片预览






文档简介
(共29张PPT)
13.1 三角形中的边角关系
第13章 三角形中的边角关系、命题与证明
13.1.3 三角形中几条重要线段
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形的高
三角形的角平分线
三角形的中线
知1-讲
知识点
三角形的高
1
1. 三角形的高的定义、性质和判定
定义 从三角形的一个顶点到它对边所在直线的垂线段叫作三角形的高线,也叫作三角形的高
图形
知1-讲
续表
性质 因为AD是△ABC的边BC上的高(已知),
所以AD⊥BC于点D(或∠ADB=∠ADC=90°)
判定 因为AD⊥BC于点D(或∠ADB=∠ADC=90°) (已知),
所以线段AD是△ABC的边BC上的高(高的定义)
知1-讲
特别提醒
作三角形某边上的高的方法:
1. 找出该边所对的顶点;
2. 过此顶点作该边的垂线,垂线段为该边上的高.
知1-讲
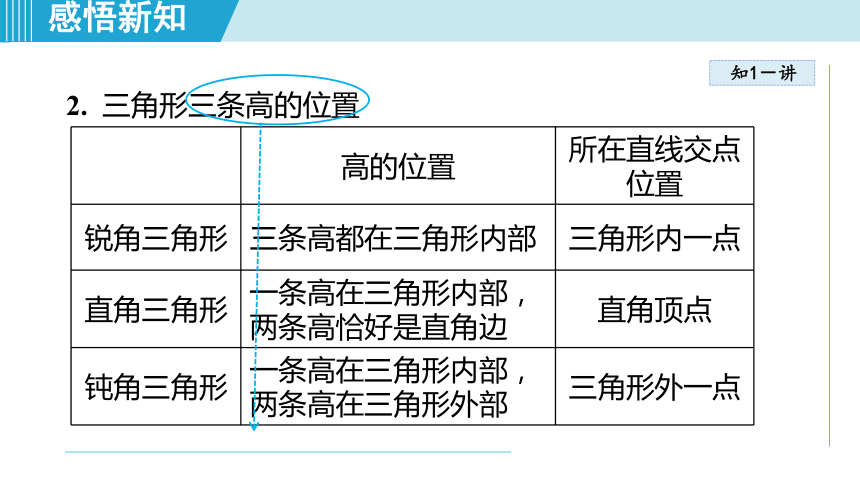
2. 三角形三条高的位置
高的位置 所在直线交点位置
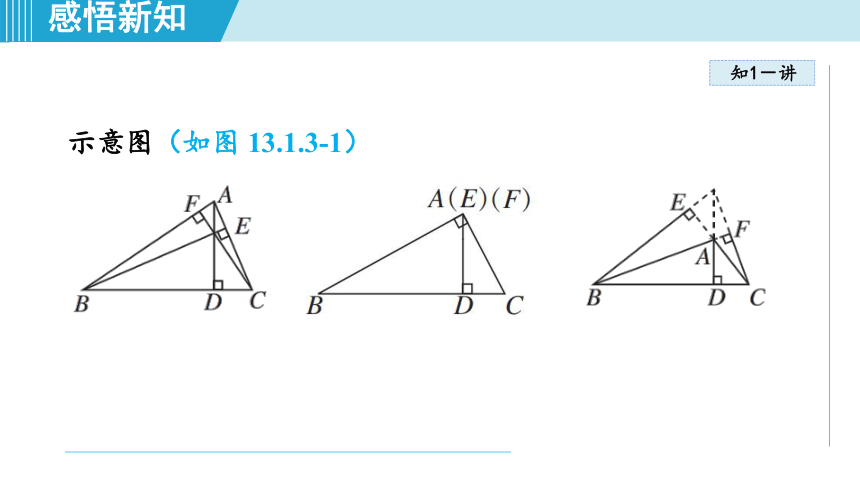
锐角三角形 三条高都在三角形内部 三角形内一点
直角三角形 一条高在三角形内部,两条高恰好是直角边 直角顶点
钝角三角形 一条高在三角形内部,两条高在三角形外部 三角形外一点
知1-讲
示意图(如图 13.1.3-1)
知1-练
如图13.1.3-2,AE⊥EC于点E,CD⊥AD于点D,AD交EC于点B.
例1
(1)△ABC的边BC上的高为_____,
边AB上的高为_____;
AE
(2)若AB=5,BC=2,CD=,则AE=_____.
CD
知1-练
解题秘方:紧扣“三角形高的定义”进行识别;
解:△ABC是钝角三角形,由三角形高的定义和钝角三角形高的位置可知,组成钝角的两条边上的高在三角形的外部,故边BC上的高为AE,边AB上的高为CD.
(1)△ABC的边BC上的高为_____,边AB上的高为_____;
知1-练
解题秘方:分别以BC,AB为底边计算△ABC的面积,列式求解.
解:因为S△ABC=BC·AE=AB·CD,
所以×2×AE=×5×,所以AE=.
(2)若AB=5,BC=2,CD=,则AE=_____.
知1-练
1-1. 如图,在△ABC中,∠C=90°.
(1)指出图中BC,AC边上的高.
(2)画出AB边上的高CD.
解:BC边上的高是AC,AC边上的高是BC.
画出AB边上的高CD如图所示.
知1-练
(3)在(2)的条件下,图中有几个直角三角形?分别表示出来.
解:图中有3个直角三角形,分别是直角三角形ABC,直角三角形ACD,直角三角形BCD.
知1-练
(4)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
知识点
三角形的角平分线
知2-讲
2
定义 三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫作三角形的角平分线.
知2-讲
特别提醒
1.角的平分线是一条射线,而三角形的角平分线是一条线段.
2.三角形的角平分线是其内角的平分线的一部分. 故角的平分线的性质三角形的角平分线都具有.
知2-讲
几何语言:如图13 .1.3 -3,
(1)AD是△ABC的角平分线;
(2)AD平分∠BAC交BC于点D;
(3)∠BAD=∠CAD=∠BAC.
知2-练
例2
如图13.1.3-4,在△ABC中,AD为△ABC的角平分线,BE⊥AC于点E,∠C=70°,∠ABC=48°,那么∠3=( )
A. 59°
B. 60°
C. 56°
D. 22°
知2-练
解题秘方:紧扣角平分线的定义,再利用三角形的内角和等于180°列式计算即可得解.
解:因为BE⊥AC,所以∠AEB=90°.因为∠C=70°,∠ABC=48°,所以∠CAB=62°.因为AD是△ABC的角平分线,所以∠1=∠CAB=31°.所以∠EFA=180°-31°-90°=59°,所以∠3=∠EFA=59°.
答案:A
知2-练
2-1. [期末· 宿州] 如图,AB∥CD,CE⊥CD于点C,∠BAE为钝角,∠BAE的平分线与∠AEC的平分线交于点F,则∠ F 的度数为( )
A.30°
B.45°
C.50°
D.无法确定
B
知3-讲
知识点
三角形的中线
3
1. 定义 三角形中,连接一个顶点与它对边中点的线段叫作三角形的中线.
知3-讲
几何语言:如图13.1.3 -5,
(1)AD是△ABC中BC边上的中线;
(2)D是BC边的中点;
(3)BD=DC,BD=BC,DC=BC(或BD=DC=BC).
知3-讲
2. 三角形的重心 三角形的三条中线相交于一点,这个交点就是三角形的重心(如图13.1.3 - 6中的点O).重心在三角形内部.
知3-讲
特别解读
三角形的中线把三角形分成的两个三角形的面积和周长的关系:
1. 两个三角形的面积相等;
2. 两个三角形的周长的差等于这两个三角形另两边的差.
知3-练
[母题 教材 P72 习题 T4 ]如图13.1.3-7,在△ABC中,AD,BE分别是△ABC,△ABD的中线.
(1)若△ABD与△ADC的周长之差为3,AB=8 ,求AC的长;
(2)若S△ABC=8,求S△ABE.
例3
解题秘方:利用中线将三角形分成的两个三角形的周长之间的关系和面积之间的关系解题.
知3-练
知3-练
解:因为AD为BC边上的中线,所以BD=CD.
所以△ABD与△ADC的周长之差为(AB+AD+BD)-
(AC+AD+CD)=AB-AC.
因为△ABD与△ADC的周长之差为3,AB=8,
所以8-AC=3,解得AC=5 .
(1)若△ABD与△ADC的周长之差为3,AB=8 ,求AC的长;
知3-练
解:因为AD是△ABC的中线,S△ABC=8,
所以S△ABD=S△ABC=4 .
因为BE是△ABD的中线,所以S△ABE=S△ABD=2 .
(2)若S△ABC=8,求S△ABE.
知3-练
3-1. [期末·亳州] 如图,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点, 且△BEF的面积是4,则△ACE的面积是( )
A. 2
B. 3
C. 4
D. 4.5
C
三角形中几条重要线段
三角形中的重要
线段
都是线段
都有三条
所在直线相交于一点
角平分线
中线
高
13.1 三角形中的边角关系
第13章 三角形中的边角关系、命题与证明
13.1.3 三角形中几条重要线段
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形的高
三角形的角平分线
三角形的中线
知1-讲
知识点
三角形的高
1
1. 三角形的高的定义、性质和判定
定义 从三角形的一个顶点到它对边所在直线的垂线段叫作三角形的高线,也叫作三角形的高
图形
知1-讲
续表
性质 因为AD是△ABC的边BC上的高(已知),
所以AD⊥BC于点D(或∠ADB=∠ADC=90°)
判定 因为AD⊥BC于点D(或∠ADB=∠ADC=90°) (已知),
所以线段AD是△ABC的边BC上的高(高的定义)
知1-讲
特别提醒
作三角形某边上的高的方法:
1. 找出该边所对的顶点;
2. 过此顶点作该边的垂线,垂线段为该边上的高.
知1-讲
2. 三角形三条高的位置
高的位置 所在直线交点位置
锐角三角形 三条高都在三角形内部 三角形内一点
直角三角形 一条高在三角形内部,两条高恰好是直角边 直角顶点
钝角三角形 一条高在三角形内部,两条高在三角形外部 三角形外一点
知1-讲
示意图(如图 13.1.3-1)
知1-练
如图13.1.3-2,AE⊥EC于点E,CD⊥AD于点D,AD交EC于点B.
例1
(1)△ABC的边BC上的高为_____,
边AB上的高为_____;
AE
(2)若AB=5,BC=2,CD=,则AE=_____.
CD
知1-练
解题秘方:紧扣“三角形高的定义”进行识别;
解:△ABC是钝角三角形,由三角形高的定义和钝角三角形高的位置可知,组成钝角的两条边上的高在三角形的外部,故边BC上的高为AE,边AB上的高为CD.
(1)△ABC的边BC上的高为_____,边AB上的高为_____;
知1-练
解题秘方:分别以BC,AB为底边计算△ABC的面积,列式求解.
解:因为S△ABC=BC·AE=AB·CD,
所以×2×AE=×5×,所以AE=.
(2)若AB=5,BC=2,CD=,则AE=_____.
知1-练
1-1. 如图,在△ABC中,∠C=90°.
(1)指出图中BC,AC边上的高.
(2)画出AB边上的高CD.
解:BC边上的高是AC,AC边上的高是BC.
画出AB边上的高CD如图所示.
知1-练
(3)在(2)的条件下,图中有几个直角三角形?分别表示出来.
解:图中有3个直角三角形,分别是直角三角形ABC,直角三角形ACD,直角三角形BCD.
知1-练
(4)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
知识点
三角形的角平分线
知2-讲
2
定义 三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫作三角形的角平分线.
知2-讲
特别提醒
1.角的平分线是一条射线,而三角形的角平分线是一条线段.
2.三角形的角平分线是其内角的平分线的一部分. 故角的平分线的性质三角形的角平分线都具有.
知2-讲
几何语言:如图13 .1.3 -3,
(1)AD是△ABC的角平分线;
(2)AD平分∠BAC交BC于点D;
(3)∠BAD=∠CAD=∠BAC.
知2-练
例2
如图13.1.3-4,在△ABC中,AD为△ABC的角平分线,BE⊥AC于点E,∠C=70°,∠ABC=48°,那么∠3=( )
A. 59°
B. 60°
C. 56°
D. 22°
知2-练
解题秘方:紧扣角平分线的定义,再利用三角形的内角和等于180°列式计算即可得解.
解:因为BE⊥AC,所以∠AEB=90°.因为∠C=70°,∠ABC=48°,所以∠CAB=62°.因为AD是△ABC的角平分线,所以∠1=∠CAB=31°.所以∠EFA=180°-31°-90°=59°,所以∠3=∠EFA=59°.
答案:A
知2-练
2-1. [期末· 宿州] 如图,AB∥CD,CE⊥CD于点C,∠BAE为钝角,∠BAE的平分线与∠AEC的平分线交于点F,则∠ F 的度数为( )
A.30°
B.45°
C.50°
D.无法确定
B
知3-讲
知识点
三角形的中线
3
1. 定义 三角形中,连接一个顶点与它对边中点的线段叫作三角形的中线.
知3-讲
几何语言:如图13.1.3 -5,
(1)AD是△ABC中BC边上的中线;
(2)D是BC边的中点;
(3)BD=DC,BD=BC,DC=BC(或BD=DC=BC).
知3-讲
2. 三角形的重心 三角形的三条中线相交于一点,这个交点就是三角形的重心(如图13.1.3 - 6中的点O).重心在三角形内部.
知3-讲
特别解读
三角形的中线把三角形分成的两个三角形的面积和周长的关系:
1. 两个三角形的面积相等;
2. 两个三角形的周长的差等于这两个三角形另两边的差.
知3-练
[母题 教材 P72 习题 T4 ]如图13.1.3-7,在△ABC中,AD,BE分别是△ABC,△ABD的中线.
(1)若△ABD与△ADC的周长之差为3,AB=8 ,求AC的长;
(2)若S△ABC=8,求S△ABE.
例3
解题秘方:利用中线将三角形分成的两个三角形的周长之间的关系和面积之间的关系解题.
知3-练
知3-练
解:因为AD为BC边上的中线,所以BD=CD.
所以△ABD与△ADC的周长之差为(AB+AD+BD)-
(AC+AD+CD)=AB-AC.
因为△ABD与△ADC的周长之差为3,AB=8,
所以8-AC=3,解得AC=5 .
(1)若△ABD与△ADC的周长之差为3,AB=8 ,求AC的长;
知3-练
解:因为AD是△ABC的中线,S△ABC=8,
所以S△ABD=S△ABC=4 .
因为BE是△ABD的中线,所以S△ABE=S△ABD=2 .
(2)若S△ABC=8,求S△ABE.
知3-练
3-1. [期末·亳州] 如图,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点, 且△BEF的面积是4,则△ACE的面积是( )
A. 2
B. 3
C. 4
D. 4.5
C
三角形中几条重要线段
三角形中的重要
线段
都是线段
都有三条
所在直线相交于一点
角平分线
中线
高
