13.1.2 三角形中角的关系 课件(共20张PPT) 2025-2026学年沪科版八年级数学上册
文档属性
| 名称 | 13.1.2 三角形中角的关系 课件(共20张PPT) 2025-2026学年沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 13:26:26 | ||
图片预览







文档简介
(共20张PPT)
13.1 三角形中的边角关系
第13章 三角形中的边角关系、命题与证明
13.1.2 三角形中角的关系
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形的内角和定理
三角形按角分类
知1-讲
知识点
三角形的内角和定理
1
1. 定理 三角形的内角和等于180°.
几何语言:在△ABC中,∠A+∠B+∠C=180°.
知1-讲
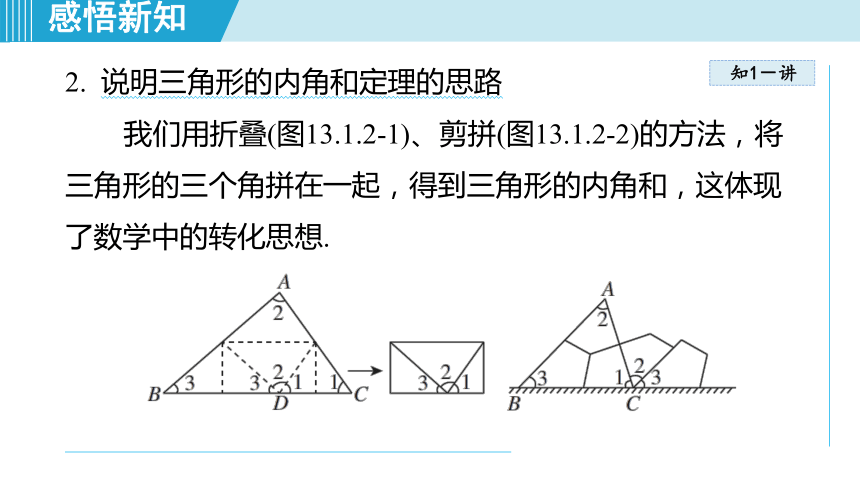
2. 说明三角形的内角和定理的思路
我们用折叠(图13.1.2-1)、剪拼(图13.1.2-2)的方法,将三角形的三个角拼在一起,得到三角形的内角和,这体现了数学中的转化思想.
知1-讲
特别解读
“三角形的内角和等于180°”揭示了三角形的三个内角之间的数量关系. 若已知三角形中任意两个角的度数,则可以求得第三个角的度数;若已知三个角的关系或三个角的度数之比,可以求各个角的度数.
知1-练
[母题 教材 P68 练习 T1 ]∠A,∠B,∠C是△ABC的
三个内角.
(1)已知∠A=40°,∠B=∠C,求∠B,∠C的度数;
(2)已知∠A-∠B=16°,∠C=54°,求∠A,∠B 的度数;
(3)已知∠A=∠B=∠C,求∠A,∠B,∠C的度数.
例1
解题秘方:紧扣三角形的内角和定理建立方程(组)求解.
(1)已知∠A=40°,∠B=∠C,求∠B,∠C的度数;
知1-练
解:设∠B=∠C=x°,
因为∠A+∠B+∠C=18 0°,∠A=40°,
所以40+x+x=180,
解得x=70,所以∠B=∠C=70°.
(2)已知∠A-∠B=16°,∠C=54°,求∠A,∠B 的度数;
知1-练
解:设∠A=a°,∠B=b°,
因为∠A-∠B=16°,∠A+∠B+∠C=180°,
∠C=54°,
所以解得
所以∠A=71°,∠B=55°.
(3)已知∠A=∠B=∠C,求∠A,∠B,∠C的度数.
知1-练
解:因为∠A=∠B=∠C,
所以∠B=2∠A,∠C=3∠ A.
设∠A=c°,则∠B=2c°,∠C=3c°,
因为∠A+∠B+∠C=180°,所以c+2c+3c=180,
解得c=30 . 所以∠A=30°,∠B=60°,∠C=90°.
知1-练
1-1. [期末·亳州]如图,点 E, D 分 别 在 AB,AC 上, 若 ∠ B=35 °,∠ C=45°,则∠ 1+ ∠ 2的度数为 ________.
80°
知1-练
感悟新知
1-2. [ 期中·六安叶集区 ] 求出下列图形中 x的值.
解:(1)因为三角形内角和是180°,
所以x+39+108=180,解得x=33.
(2)因为三角形内角和是180°,
所以x+x+x=180,解得x=60.
知1-练
1-3. [期末· 合肥] 在△ABC中,∠B=3∠A,∠C=∠B+40°,求△ABC的各内角度数.
解:因为∠B=3∠A,∠C=∠B+40°,
所以∠C=3∠A+40°.
因为∠A+∠B+∠C=180°,
所以∠A+3∠A+3∠A+40°=180°,
解得∠A=20°,所以∠B=60°,∠C=100°.
知识点
三角形按角分类
知2-讲
2
1. 各类三角形的概念
(1) 锐角三角形:三角形中,三个角都是锐角的三角形叫作锐角三角形.
(2) 直角三角形:三角形中,有一个角是直角的三角形叫作直角三角形.
(3) 钝角三角形:三角形中,有一个角是钝角的三角形叫作钝角三角形.
知2-讲
2. 直角三角形的表示 直角三角形中夹直角的两边叫做直角边,直角相对的边叫做斜边,直角三角形ABC可以写成“Rt△ABC”,如图13.1.2-3所示.
知2-讲
3. 三角形按角的大小分类
三角形
知2-讲
拓展
1. 三角形的内角中,最多有一个直角或一个钝角,最少有两个锐角.
2. 三角形按边分类和按角分类是两种不同的分类方式,各自独立,无论按哪种标准分类,原则都是不重不漏.
3. 等腰直角三角形,按边分类属于等腰三角形,按角分类属于直角三角形.
知2-练
例2
根据下列所给条件,判断△ABC的形状.
(1)∠A=40°,∠B=60°,∠C=80°;
(2)∠C=120°;
(3)∠C=90°.
解题秘方:紧扣三角形分类的标准进行辨析. 按角分类的关键是先观察一个三角形中是否有直角或钝角.
知2-练
解:(1)因为三个角都是锐角,所以△ABC是锐角三角形.
(2)因为∠C=120°>90°,所以△ABC是钝角三角形.
(3)因为∠C=90°,所以△ABC是直角三角形.
方法点拨:由角的大小判断三角形形状的方法:
(1)若最大角为锐角,则该三角形为锐角三角形;
(2)若最大角为直角,则该三角形为直角三角形;
(3)若最大角为钝角,则该三角形为钝角三角形.
知2-练
2-1. 如图,一个三角形被木板遮掩了一部分,则这个三角形为( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
D
三角形中角的关系
三角
形中
角的
关系
按角的大
小分类
锐角三角形
钝角三角形
三个内角的
数量关系
内角和
等于180°
直角三角形
13.1 三角形中的边角关系
第13章 三角形中的边角关系、命题与证明
13.1.2 三角形中角的关系
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形的内角和定理
三角形按角分类
知1-讲
知识点
三角形的内角和定理
1
1. 定理 三角形的内角和等于180°.
几何语言:在△ABC中,∠A+∠B+∠C=180°.
知1-讲
2. 说明三角形的内角和定理的思路
我们用折叠(图13.1.2-1)、剪拼(图13.1.2-2)的方法,将三角形的三个角拼在一起,得到三角形的内角和,这体现了数学中的转化思想.
知1-讲
特别解读
“三角形的内角和等于180°”揭示了三角形的三个内角之间的数量关系. 若已知三角形中任意两个角的度数,则可以求得第三个角的度数;若已知三个角的关系或三个角的度数之比,可以求各个角的度数.
知1-练
[母题 教材 P68 练习 T1 ]∠A,∠B,∠C是△ABC的
三个内角.
(1)已知∠A=40°,∠B=∠C,求∠B,∠C的度数;
(2)已知∠A-∠B=16°,∠C=54°,求∠A,∠B 的度数;
(3)已知∠A=∠B=∠C,求∠A,∠B,∠C的度数.
例1
解题秘方:紧扣三角形的内角和定理建立方程(组)求解.
(1)已知∠A=40°,∠B=∠C,求∠B,∠C的度数;
知1-练
解:设∠B=∠C=x°,
因为∠A+∠B+∠C=18 0°,∠A=40°,
所以40+x+x=180,
解得x=70,所以∠B=∠C=70°.
(2)已知∠A-∠B=16°,∠C=54°,求∠A,∠B 的度数;
知1-练
解:设∠A=a°,∠B=b°,
因为∠A-∠B=16°,∠A+∠B+∠C=180°,
∠C=54°,
所以解得
所以∠A=71°,∠B=55°.
(3)已知∠A=∠B=∠C,求∠A,∠B,∠C的度数.
知1-练
解:因为∠A=∠B=∠C,
所以∠B=2∠A,∠C=3∠ A.
设∠A=c°,则∠B=2c°,∠C=3c°,
因为∠A+∠B+∠C=180°,所以c+2c+3c=180,
解得c=30 . 所以∠A=30°,∠B=60°,∠C=90°.
知1-练
1-1. [期末·亳州]如图,点 E, D 分 别 在 AB,AC 上, 若 ∠ B=35 °,∠ C=45°,则∠ 1+ ∠ 2的度数为 ________.
80°
知1-练
感悟新知
1-2. [ 期中·六安叶集区 ] 求出下列图形中 x的值.
解:(1)因为三角形内角和是180°,
所以x+39+108=180,解得x=33.
(2)因为三角形内角和是180°,
所以x+x+x=180,解得x=60.
知1-练
1-3. [期末· 合肥] 在△ABC中,∠B=3∠A,∠C=∠B+40°,求△ABC的各内角度数.
解:因为∠B=3∠A,∠C=∠B+40°,
所以∠C=3∠A+40°.
因为∠A+∠B+∠C=180°,
所以∠A+3∠A+3∠A+40°=180°,
解得∠A=20°,所以∠B=60°,∠C=100°.
知识点
三角形按角分类
知2-讲
2
1. 各类三角形的概念
(1) 锐角三角形:三角形中,三个角都是锐角的三角形叫作锐角三角形.
(2) 直角三角形:三角形中,有一个角是直角的三角形叫作直角三角形.
(3) 钝角三角形:三角形中,有一个角是钝角的三角形叫作钝角三角形.
知2-讲
2. 直角三角形的表示 直角三角形中夹直角的两边叫做直角边,直角相对的边叫做斜边,直角三角形ABC可以写成“Rt△ABC”,如图13.1.2-3所示.
知2-讲
3. 三角形按角的大小分类
三角形
知2-讲
拓展
1. 三角形的内角中,最多有一个直角或一个钝角,最少有两个锐角.
2. 三角形按边分类和按角分类是两种不同的分类方式,各自独立,无论按哪种标准分类,原则都是不重不漏.
3. 等腰直角三角形,按边分类属于等腰三角形,按角分类属于直角三角形.
知2-练
例2
根据下列所给条件,判断△ABC的形状.
(1)∠A=40°,∠B=60°,∠C=80°;
(2)∠C=120°;
(3)∠C=90°.
解题秘方:紧扣三角形分类的标准进行辨析. 按角分类的关键是先观察一个三角形中是否有直角或钝角.
知2-练
解:(1)因为三个角都是锐角,所以△ABC是锐角三角形.
(2)因为∠C=120°>90°,所以△ABC是钝角三角形.
(3)因为∠C=90°,所以△ABC是直角三角形.
方法点拨:由角的大小判断三角形形状的方法:
(1)若最大角为锐角,则该三角形为锐角三角形;
(2)若最大角为直角,则该三角形为直角三角形;
(3)若最大角为钝角,则该三角形为钝角三角形.
知2-练
2-1. 如图,一个三角形被木板遮掩了一部分,则这个三角形为( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
D
三角形中角的关系
三角
形中
角的
关系
按角的大
小分类
锐角三角形
钝角三角形
三个内角的
数量关系
内角和
等于180°
直角三角形
