小升初复习精讲精练十六《解决问题的策略》--北师大版(复习课件)
文档属性
| 名称 | 小升初复习精讲精练十六《解决问题的策略》--北师大版(复习课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 16:10:12 | ||
图片预览







文档简介
(共38张PPT)
第十六课时
解决问题的策略
(北师大)六年级
下
01
学习目标
内容总览
02
知识梳理
04
变式训练
05
培优拓展
03
典例
06
强化训练
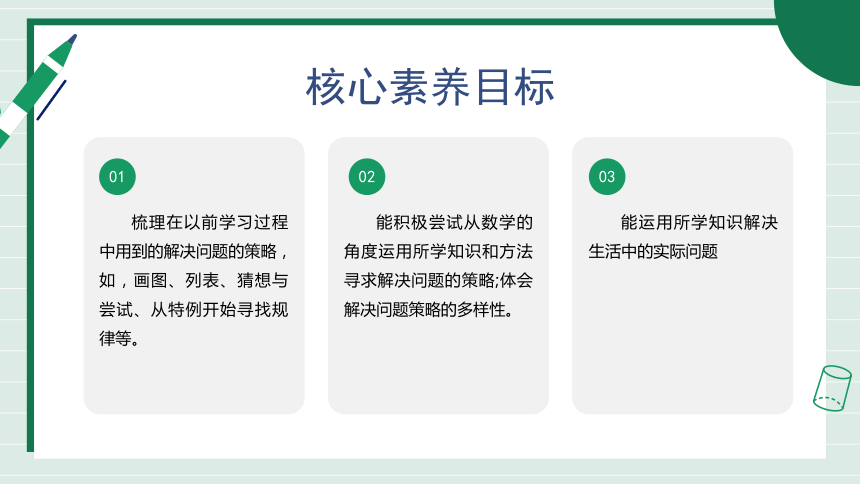
核心素养目标
梳理在以前学习过程中用到的解决问题的策略,如,画图、列表、猜想与尝试、从特例开始寻找规律等。
01
02
能积极尝试从数学的角度运用所学知识和方法寻求解决问题的策略;体会解决问题策略的多样性。
03
能运用所学知识解决生活中的实际问题
知识梳理
考点一:画图法。
(1)可以帮助我们列举出所有的情况;
(2)能帮助我们直观理解;
(3)能帮助我们分析数量之间的关系。
知识梳理
考点二:列表法
列表可以帮助我们整理信息,进行推理;
也可以帮助我们分析两个量之间的关系,寻找规律。
知识梳理
考点三:猜想与尝试
1.用猜想与尝试法解决鸡免同笼问题,一般从各为半数开始,便于确定鸡的只数多了还是兔的只数多了,从而进一步调整猜想思路,直到寻找出正确的答案。
2.归纳、类比是获取猜想的重要方式。
知识梳理
考点四:从特例开始寻找规律
从特例开始寻找规律:在解决较复杂问题时,先从简单的情形开始,把简单的问题的解决方法逐渐推广到较复杂的问题然后总结出规律,使复杂的问题得到解决。
典例
人们在解决问题时,使用一定的策略是非常重要的。常见的解决问题的策略有哪些?
画图
列表
猜想与尝试
从特例开始
寻找规律
典例
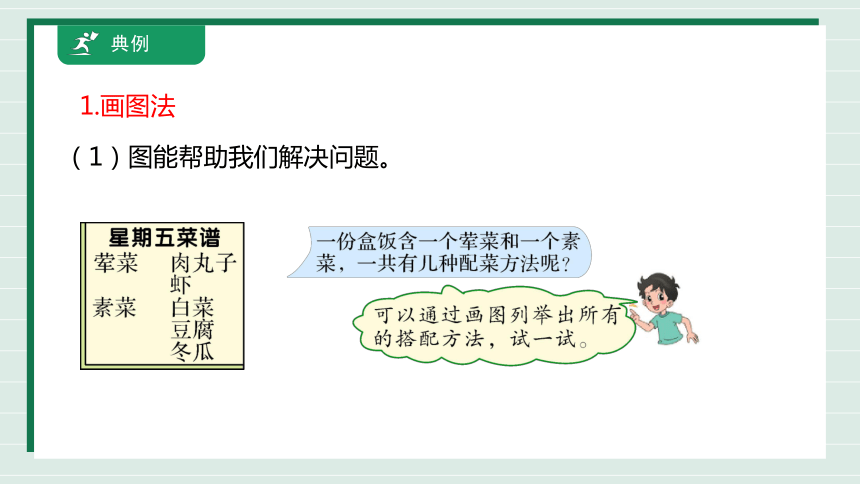
(1)图能帮助我们解决问题。
1.画图法
典例
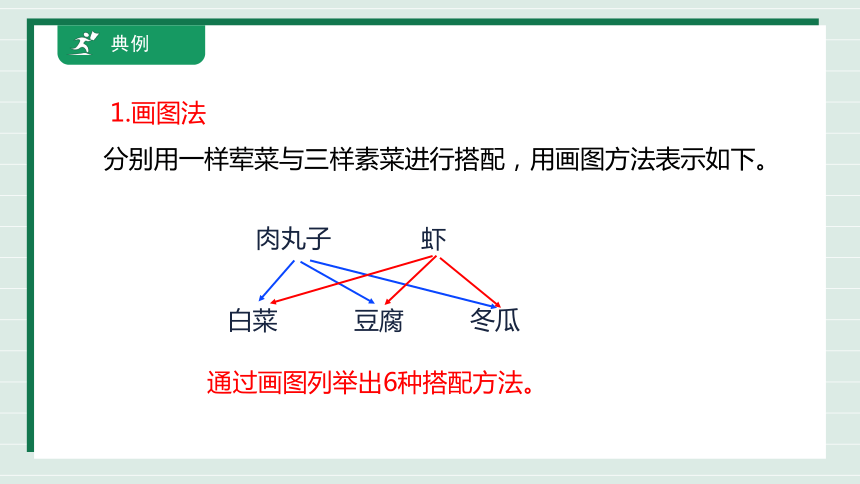
分别用一样荤菜与三样素菜进行搭配,用画图方法表示如下。
肉丸子
虾
白菜
豆腐
冬瓜
通过画图列举出6种搭配方法。
1.画图法
典例
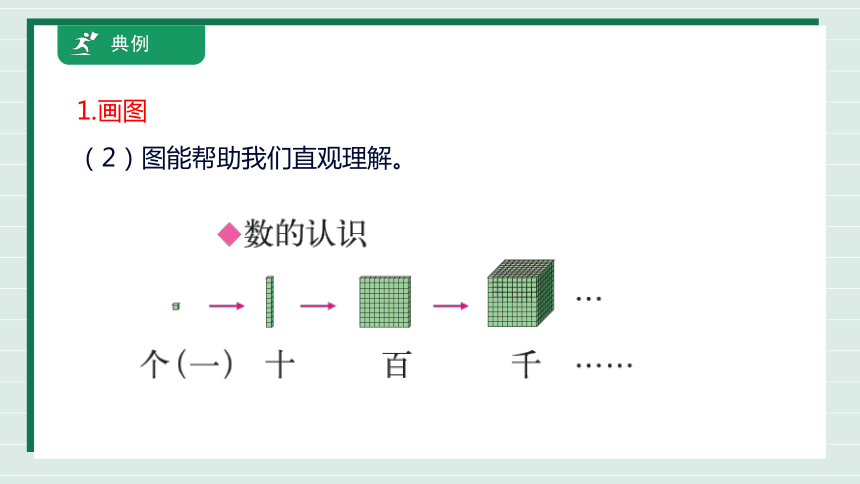
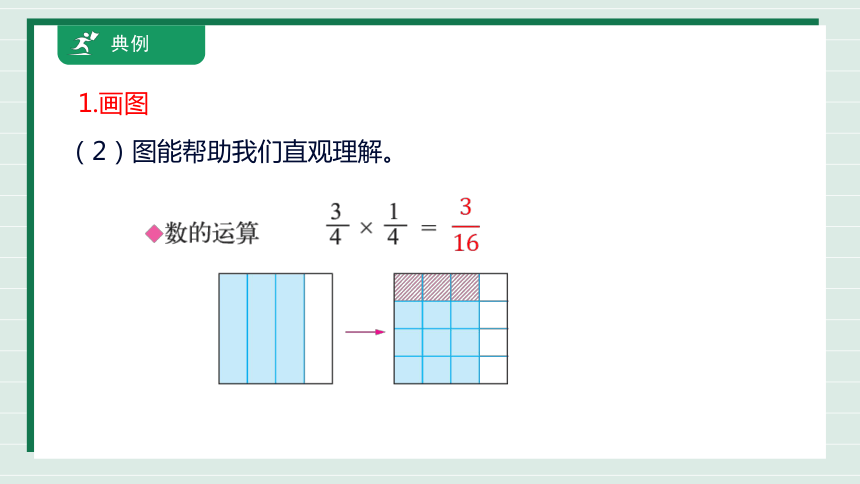
1.画图
(2)图能帮助我们直观理解。
典例
1.画图
(2)图能帮助我们直观理解。
典例
典例
1.画图法
(2)图能帮助我们直观理解。
变化的量之间的关系。
说一说公共汽车从解放路站到商场站之间,行驶的时间与速度之间的关系。
公共汽车从解放路站行驶的时间与速度之间成正比例的关系。
典例
1.画图
(3)图能帮助我们分析问题中的数量关系。
可得数量关系式:
第一天的成交量×(1+ )=第二天的成交量
答:第二天的成交量是78辆。
65×(1+)=78(辆)
典例
(1)学校组织了足球、航模和电脑兴趣小组,淘气、笑笑和奇思分别参加了其中一项。笑笑不喜欢踢足球,淘气不是电脑兴趣小组的,奇思喜欢航模。画一个表来帮忙,把信息记录下来,并进行整理。
2.列表法
足球 航模 电脑
淘气
笑笑
奇思
√
x
x
√
√
典例
列表也能帮助我们分析两个量之间的关系,寻找规律。
(2)下表是妙想体重的变化情况。
从上统计表可以看出妙想10岁前体重是随年龄增长而增加。
年龄 出生时 6个月 1岁 2岁 6岁 10岁
体重/kg 3.5 7.0 10.5 14.0 21.0 31.5
说一说妙想10岁前体重是如何随年龄增长而变化的。
2.列表法
典例
(1)鸡兔同笼,有20个头,54条腿,鸡、兔各有多少只?
3.猜想与尝试
头/个 鸡/只 兔/只 腿/条
20 10 10 60
20
20
20
假设鸡兔各半,60条腿多了,说明鸡多,兔少。
11
9
58
12
8
56
鸡兔换一只,腿少2条。
13
7
54
在猜想中尝试,在尝试中发现规律,不断调整,找到正确的方法。
典例
(2)
V=sh
V=sh
长方体、正方体的体积等于底面积乘高。圆柱的体积呢?
验证你的猜想。
典例
V S h
V = Sh
长方体体积 = 长 × 宽 × 高
圆柱体积 =
圆柱底面周长的一半
圆柱底面半径
圆柱的高
圆柱底面周长的一半
圆柱底面半径
圆柱的高
×
×
底面积
× 高
圆柱体积=
典例
参加比赛人数 示意图 各点之间连线数 比赛场数
2 1 1
3 1+2= 3
4 1+2+3= 6
…… …… …… ……
六一班10名同学进行乒乓球比赛,如果每2名同学之间都进行一场比赛,一个要比赛多少场?
9+8+7+6+5+4+3+2+1=45(场)
4.从特例开始寻找规律
典例
爷爷用24根1米长的栅栏围成一个长方形羊圈,爷爷有几种围法?围成的面积最大是多少平方米?
长/m
宽/m
面积/m2
11
11
1
①
10
2
②
9
3
③
8
4
④
7
5
⑤
6
6
⑥
长+宽的和:24 ÷ 2=12(m)
20
27
32
35
36
长和宽越接近,面积越大
典例
原有( )张
+24张
( )张
-30张
52张
-24
+30
52+30-24=58(张)
小云原来有一些邮票,今年又收集了24张,她送给小娟30张后,还剩52张,小云原来有多少张邮票?
答:小云原来有58张邮票。
5.逆推法
典例
6.转化法
h
a
S= ah
2
1
(1)求三角形的面积。
(2)求梯形的面积。
典例
6.转化法
梯形上底+梯形下底
高
S =(a+b)h÷2
(3)求梯形的面积。
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
r
C
2
(4)求圆的面积。
变式练习
1.小明从一楼走到三楼,一共走了 48 级台阶他如果从一楼走到五楼,一共要走多少级台阶 (每一层台阶数都一样多)
答:一共要走 96 级合阶。
48÷(3-1)x(5-1)
=48÷2x4
=96(级)
变式练习
2.刘老师带 45 名同学去划船,共租了10条船。每条大船坐6人,每条小船坐4人,恰好坐满。大船、小船各租了几条
45+1=46(人)
从假设大船、小船各租了5条开始列表。
答:大船租了3条,小船租了7条。
大船/条 小船/余 船的总数/条 可坐人数/人
5 5 10 50
4 6 10 48
3 7 10 46
变式练习
3.王明步行从家出发去图书馆,借完书后骑共享单车回家。下图表示在这段时间里王明离家的距离变化情况。
1.王明在图书馆停留了( )分。
2.王明家距离图书馆有( )km。
3.王明从图书馆回家时平均每分骑行( )km。
60
5
0.25
变式练习
4.找规律填数。
课堂总结
今天你有什么收获?
培优拓展
1.现有若干个圆环,它们的外直径都是5cm,环宽是5mm,将它们扣在一起(如图)拉紧后测量总长度。
像这样,10 个圆环拉紧后的长度是( )cm,( )个圆环拉紧后的长度是73cm。如果圆环的个数为n,拉紧后的总长度是( )cm。
41
18
4n+1
培优拓展
2.观察下面点图与算式的关系,找出规律解答问题。
(1)按点增加的规律给第⑤个图补上点,并写出算式。
(2)根据图中点的总数的变化规律,第n个图中共有( )个点。
(用含有字母n的式子表示)
n
培优拓展
3.计算。
强化训练
1.学校举办乒乓球单打循环赛,一共有7人参加,每两名参赛人员之间都有一场比赛,一共要赛多少场
6+5+4+3+2+1=21(场)
答:一共要赛21 场。
强化训练
2.从2张10元、4张5元、8张1元的人民币中取出 20 元,有多少种不同的取法 请分别写出来。
答:有5种不同的取法。
10元/张 5元/张 1元/张
1 2
2 1 2
3 1 1 5
4 4
5 3 5
强化训练
3.某公园有一块长方形草坪,如果把草坪的长增加10m,或者宽增加5m,面积都比原来增加 200m 。这块长方形草坪原来的面积是多少平方米
原来长方形草坪的宽:200÷10=20(m)原来长方形草坪的长:200÷5=40(m)原来长方形草坪的面积:40x20=800(m )
答:这块长方形草坪原来的面积是(800)m 。
强化训练
4.用小棒按下图方式摆正方形,观察并填表。
正方形个数 1 2 3 4 …… n
小棒 根数 4 7 31 ……
10
13
10
3n+1
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
第十六课时
解决问题的策略
(北师大)六年级
下
01
学习目标
内容总览
02
知识梳理
04
变式训练
05
培优拓展
03
典例
06
强化训练
核心素养目标
梳理在以前学习过程中用到的解决问题的策略,如,画图、列表、猜想与尝试、从特例开始寻找规律等。
01
02
能积极尝试从数学的角度运用所学知识和方法寻求解决问题的策略;体会解决问题策略的多样性。
03
能运用所学知识解决生活中的实际问题
知识梳理
考点一:画图法。
(1)可以帮助我们列举出所有的情况;
(2)能帮助我们直观理解;
(3)能帮助我们分析数量之间的关系。
知识梳理
考点二:列表法
列表可以帮助我们整理信息,进行推理;
也可以帮助我们分析两个量之间的关系,寻找规律。
知识梳理
考点三:猜想与尝试
1.用猜想与尝试法解决鸡免同笼问题,一般从各为半数开始,便于确定鸡的只数多了还是兔的只数多了,从而进一步调整猜想思路,直到寻找出正确的答案。
2.归纳、类比是获取猜想的重要方式。
知识梳理
考点四:从特例开始寻找规律
从特例开始寻找规律:在解决较复杂问题时,先从简单的情形开始,把简单的问题的解决方法逐渐推广到较复杂的问题然后总结出规律,使复杂的问题得到解决。
典例
人们在解决问题时,使用一定的策略是非常重要的。常见的解决问题的策略有哪些?
画图
列表
猜想与尝试
从特例开始
寻找规律
典例
(1)图能帮助我们解决问题。
1.画图法
典例
分别用一样荤菜与三样素菜进行搭配,用画图方法表示如下。
肉丸子
虾
白菜
豆腐
冬瓜
通过画图列举出6种搭配方法。
1.画图法
典例
1.画图
(2)图能帮助我们直观理解。
典例
1.画图
(2)图能帮助我们直观理解。
典例
典例
1.画图法
(2)图能帮助我们直观理解。
变化的量之间的关系。
说一说公共汽车从解放路站到商场站之间,行驶的时间与速度之间的关系。
公共汽车从解放路站行驶的时间与速度之间成正比例的关系。
典例
1.画图
(3)图能帮助我们分析问题中的数量关系。
可得数量关系式:
第一天的成交量×(1+ )=第二天的成交量
答:第二天的成交量是78辆。
65×(1+)=78(辆)
典例
(1)学校组织了足球、航模和电脑兴趣小组,淘气、笑笑和奇思分别参加了其中一项。笑笑不喜欢踢足球,淘气不是电脑兴趣小组的,奇思喜欢航模。画一个表来帮忙,把信息记录下来,并进行整理。
2.列表法
足球 航模 电脑
淘气
笑笑
奇思
√
x
x
√
√
典例
列表也能帮助我们分析两个量之间的关系,寻找规律。
(2)下表是妙想体重的变化情况。
从上统计表可以看出妙想10岁前体重是随年龄增长而增加。
年龄 出生时 6个月 1岁 2岁 6岁 10岁
体重/kg 3.5 7.0 10.5 14.0 21.0 31.5
说一说妙想10岁前体重是如何随年龄增长而变化的。
2.列表法
典例
(1)鸡兔同笼,有20个头,54条腿,鸡、兔各有多少只?
3.猜想与尝试
头/个 鸡/只 兔/只 腿/条
20 10 10 60
20
20
20
假设鸡兔各半,60条腿多了,说明鸡多,兔少。
11
9
58
12
8
56
鸡兔换一只,腿少2条。
13
7
54
在猜想中尝试,在尝试中发现规律,不断调整,找到正确的方法。
典例
(2)
V=sh
V=sh
长方体、正方体的体积等于底面积乘高。圆柱的体积呢?
验证你的猜想。
典例
V S h
V = Sh
长方体体积 = 长 × 宽 × 高
圆柱体积 =
圆柱底面周长的一半
圆柱底面半径
圆柱的高
圆柱底面周长的一半
圆柱底面半径
圆柱的高
×
×
底面积
× 高
圆柱体积=
典例
参加比赛人数 示意图 各点之间连线数 比赛场数
2 1 1
3 1+2= 3
4 1+2+3= 6
…… …… …… ……
六一班10名同学进行乒乓球比赛,如果每2名同学之间都进行一场比赛,一个要比赛多少场?
9+8+7+6+5+4+3+2+1=45(场)
4.从特例开始寻找规律
典例
爷爷用24根1米长的栅栏围成一个长方形羊圈,爷爷有几种围法?围成的面积最大是多少平方米?
长/m
宽/m
面积/m2
11
11
1
①
10
2
②
9
3
③
8
4
④
7
5
⑤
6
6
⑥
长+宽的和:24 ÷ 2=12(m)
20
27
32
35
36
长和宽越接近,面积越大
典例
原有( )张
+24张
( )张
-30张
52张
-24
+30
52+30-24=58(张)
小云原来有一些邮票,今年又收集了24张,她送给小娟30张后,还剩52张,小云原来有多少张邮票?
答:小云原来有58张邮票。
5.逆推法
典例
6.转化法
h
a
S= ah
2
1
(1)求三角形的面积。
(2)求梯形的面积。
典例
6.转化法
梯形上底+梯形下底
高
S =(a+b)h÷2
(3)求梯形的面积。
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
r
C
2
(4)求圆的面积。
变式练习
1.小明从一楼走到三楼,一共走了 48 级台阶他如果从一楼走到五楼,一共要走多少级台阶 (每一层台阶数都一样多)
答:一共要走 96 级合阶。
48÷(3-1)x(5-1)
=48÷2x4
=96(级)
变式练习
2.刘老师带 45 名同学去划船,共租了10条船。每条大船坐6人,每条小船坐4人,恰好坐满。大船、小船各租了几条
45+1=46(人)
从假设大船、小船各租了5条开始列表。
答:大船租了3条,小船租了7条。
大船/条 小船/余 船的总数/条 可坐人数/人
5 5 10 50
4 6 10 48
3 7 10 46
变式练习
3.王明步行从家出发去图书馆,借完书后骑共享单车回家。下图表示在这段时间里王明离家的距离变化情况。
1.王明在图书馆停留了( )分。
2.王明家距离图书馆有( )km。
3.王明从图书馆回家时平均每分骑行( )km。
60
5
0.25
变式练习
4.找规律填数。
课堂总结
今天你有什么收获?
培优拓展
1.现有若干个圆环,它们的外直径都是5cm,环宽是5mm,将它们扣在一起(如图)拉紧后测量总长度。
像这样,10 个圆环拉紧后的长度是( )cm,( )个圆环拉紧后的长度是73cm。如果圆环的个数为n,拉紧后的总长度是( )cm。
41
18
4n+1
培优拓展
2.观察下面点图与算式的关系,找出规律解答问题。
(1)按点增加的规律给第⑤个图补上点,并写出算式。
(2)根据图中点的总数的变化规律,第n个图中共有( )个点。
(用含有字母n的式子表示)
n
培优拓展
3.计算。
强化训练
1.学校举办乒乓球单打循环赛,一共有7人参加,每两名参赛人员之间都有一场比赛,一共要赛多少场
6+5+4+3+2+1=21(场)
答:一共要赛21 场。
强化训练
2.从2张10元、4张5元、8张1元的人民币中取出 20 元,有多少种不同的取法 请分别写出来。
答:有5种不同的取法。
10元/张 5元/张 1元/张
1 2
2 1 2
3 1 1 5
4 4
5 3 5
强化训练
3.某公园有一块长方形草坪,如果把草坪的长增加10m,或者宽增加5m,面积都比原来增加 200m 。这块长方形草坪原来的面积是多少平方米
原来长方形草坪的宽:200÷10=20(m)原来长方形草坪的长:200÷5=40(m)原来长方形草坪的面积:40x20=800(m )
答:这块长方形草坪原来的面积是(800)m 。
强化训练
4.用小棒按下图方式摆正方形,观察并填表。
正方形个数 1 2 3 4 …… n
小棒 根数 4 7 31 ……
10
13
10
3n+1
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
同课章节目录
