数学:25.3利用频率估计概率(第2课时)课件(人教新课标九年级上)
文档属性
| 名称 | 数学:25.3利用频率估计概率(第2课时)课件(人教新课标九年级上) |
|
|
| 格式 | rar | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-15 00:00:00 | ||
图片预览




文档简介
课件10张PPT。用频率估计概率用列举法求概率的条件是什么?(1)实验的所有结果是有限个(n)
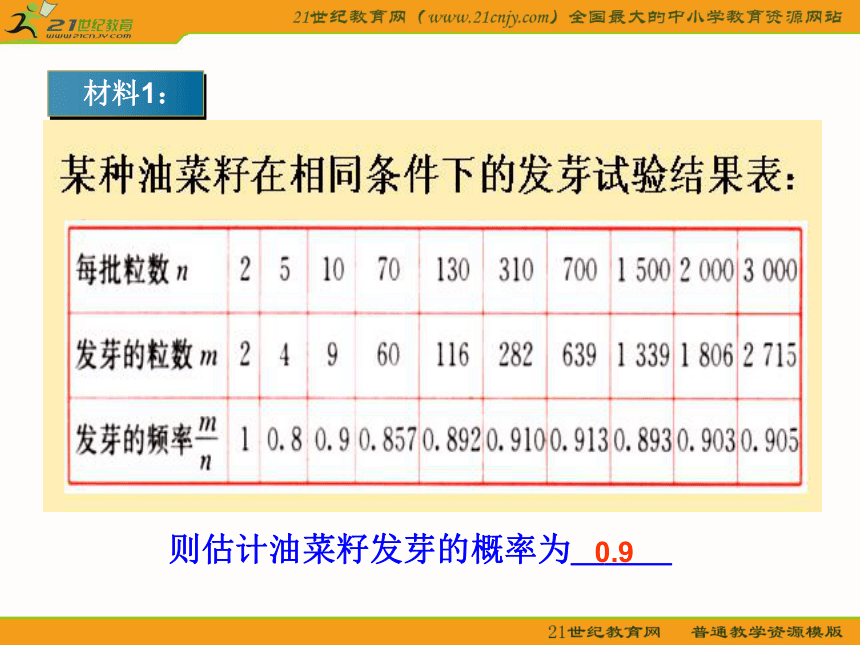
(2)各种结果的可能性相等. 当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?问题1:某林业部门要考查某种幼树在一定条件下的移植成活率,应采取什么具体做法? 该问题不属于结果可能性相等的类型.移植中有两种情况活或死.它们的可能性并不相等, 事件发生的概率并不都为50%.则估计油菜籽发芽的概率为___0.9 结 论 瑞士数学家雅各布.伯努利(1654-1705)最早阐明了可以由频率估计概率即: 在相同的条件下,大量的重复实验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率 例1、某水果公司以2元/千克的成本新进了10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率“统计,并把获得的数据记录在下表中了。0.1100.1050.1010.0970.0970.1010.1010.0980.0990.103(2)根据表中数据填空:
这批柑橘损坏的概率是______,则完好柑橘的概率是_______,
如果某水果公司以2元/千克的成本进了10000千克柑橘,则这批柑橘中完好柑橘的质量是________,若公司希望这些柑橘能够获利5000元,那么售价应定为_______元/千克比较合适. 0.10.990002.8在相同情况下随机的抽取若干个体进行实验,
进行实验统计.并计算事件发生的频率
根据频率估计该事件发生的概率. 当试验次数很大时,一个事件发生频率也稳定在相应的概率附近.因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼_______尾,鲢鱼_______尾.310270 2.在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?解:
根据概率的意义,可以认为其概率大约等于250/2000=0.125.
该镇约有100000×0.125=12500人看中央电视台的早间新闻.
(2)各种结果的可能性相等. 当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?问题1:某林业部门要考查某种幼树在一定条件下的移植成活率,应采取什么具体做法? 该问题不属于结果可能性相等的类型.移植中有两种情况活或死.它们的可能性并不相等, 事件发生的概率并不都为50%.则估计油菜籽发芽的概率为___0.9 结 论 瑞士数学家雅各布.伯努利(1654-1705)最早阐明了可以由频率估计概率即: 在相同的条件下,大量的重复实验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率 例1、某水果公司以2元/千克的成本新进了10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率“统计,并把获得的数据记录在下表中了。0.1100.1050.1010.0970.0970.1010.1010.0980.0990.103(2)根据表中数据填空:
这批柑橘损坏的概率是______,则完好柑橘的概率是_______,
如果某水果公司以2元/千克的成本进了10000千克柑橘,则这批柑橘中完好柑橘的质量是________,若公司希望这些柑橘能够获利5000元,那么售价应定为_______元/千克比较合适. 0.10.990002.8在相同情况下随机的抽取若干个体进行实验,
进行实验统计.并计算事件发生的频率
根据频率估计该事件发生的概率. 当试验次数很大时,一个事件发生频率也稳定在相应的概率附近.因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼_______尾,鲢鱼_______尾.310270 2.在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?解:
根据概率的意义,可以认为其概率大约等于250/2000=0.125.
该镇约有100000×0.125=12500人看中央电视台的早间新闻.
同课章节目录
