【高考押题卷】2025年高考物理高频易错考前冲刺 动量与动量守恒定律(含解析)
文档属性
| 名称 | 【高考押题卷】2025年高考物理高频易错考前冲刺 动量与动量守恒定律(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-28 07:57:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
高考物理高频易错押题预测 动量与动量守恒定律
一.选择题(共8小题)
1.(2025 庐阳区校级模拟)图为丁俊晖正在准备击球,设丁俊晖在某一杆击球过程中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球A的动量pA=5kg m/s,花色球B静止,碰后花色球B的动量变为P'B=4kg m/s,则两球质量mA与mB间的关系可能是( )
A. B. C.mB=2mA D.mB=5mA
2.(2024秋 南京期末)如图所示,在离地面高为h处将质量为m的小球以初速度v0水平抛出,重力加速度为g,不计空气阻力。下列说法正确的是( )
A.落地前瞬间,小球的动量大小为
B.从抛出到落地,小球所受重力的冲量大小为
C.从抛出到落地,小球动量的变化量方向竖直向上
D.从抛出到落地,小球动量的变化量大小为
3.(2024秋 扬州期末)骑电瓶车必须戴好头盔。在头部受到撞击时,其他条件相同,戴头盔与不戴头盔相比,骑行者头部( )
A.动量变化小 B.动量变化慢
C.受到撞击力大 D.受到撞击力的冲量大
4.(2024秋 徐州期末)做自由落体运动的物体,其动量p与时间t的p﹣t关系图线为( )
A. B.
C. D.
5.(2024秋 郴州期末)三个完全相同的小球,质量均为m,其中小球A、B固定在竖直轻杆的两端,A球紧贴竖直光滑墙面,B球位于足够大的光滑水平地面上,小球C紧贴小球B,如图所示,三小球均保持静止。某时,小球A受到轻微扰动开始顺着墙面下滑,直至小球A落地前瞬间的运动过程中,三小球始终在同一竖直面上。已知小球C的最大速度为v,轻杆长为L,重力加速度为g,下列关于该过程的说法中正确的是( )
A.A、B、C三球组成的系统动量守恒
B.竖直墙对小球A的冲量大小为3mv
C.小球A落地前瞬间,动能大小为
D.小球A落地前瞬间,小球C的速度是小球B速度的2倍
6.(2024秋 徐州期末)为确保公共安全,市民遛狗时应牵绳。如图所示,一市民遛狗时匀速前行,已知绳中拉力大小为F、方向与水平面夹角为θ。则在t时间内拉力的冲量为( )
A.0
B.Ft,方向与F方向一致
C.Ftcosθ,方向与F方向一致
D.Ftcosθ,方向沿水平方向向左
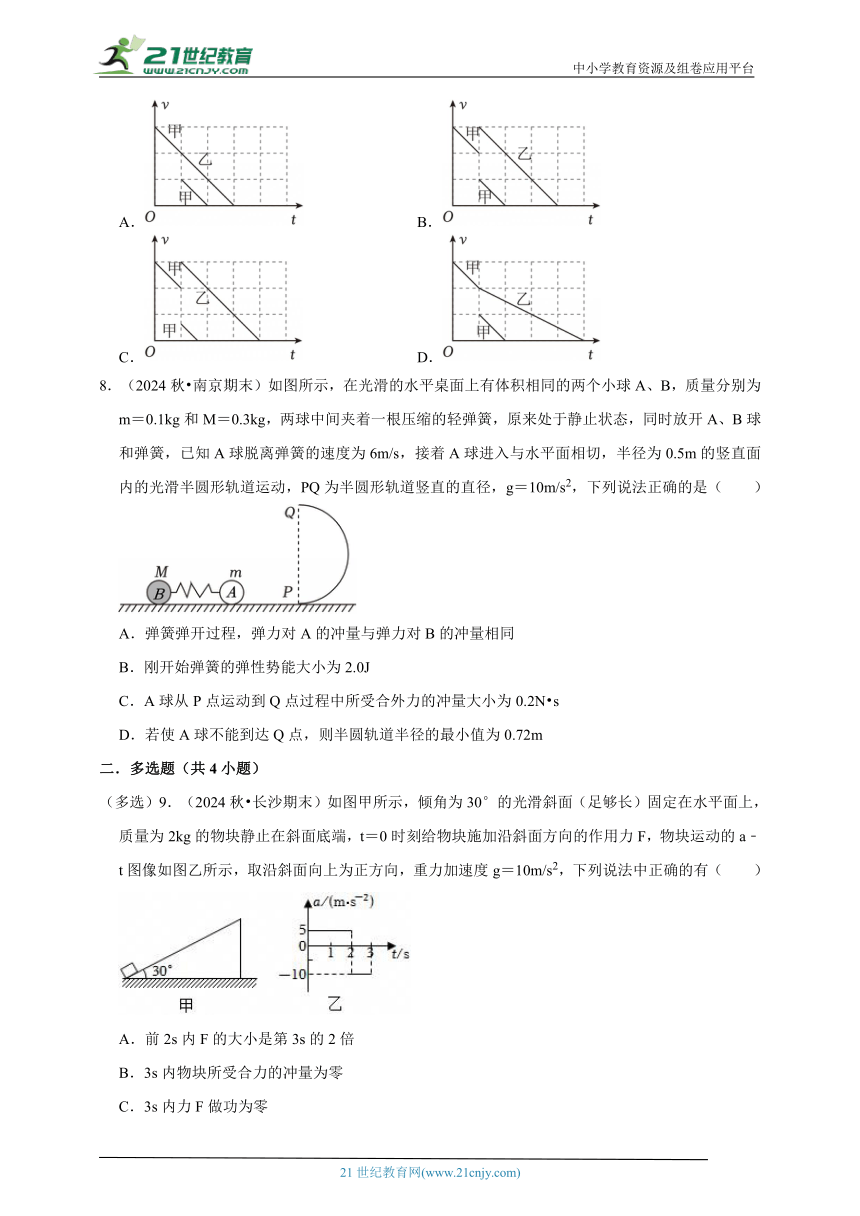
7.(2024秋 扬州期末)如图所示,在水平桌面上,粘在一起的两个一元硬币甲与静止的一元硬币乙发生一维碰撞。在下列描述甲、乙速度v与时间t的关系图像中,可能正确的是( )
A. B.
C. D.
8.(2024秋 南京期末)如图所示,在光滑的水平桌面上有体积相同的两个小球A、B,质量分别为m=0.1kg和M=0.3kg,两球中间夹着一根压缩的轻弹簧,原来处于静止状态,同时放开A、B球和弹簧,已知A球脱离弹簧的速度为6m/s,接着A球进入与水平面相切,半径为0.5m的竖直面内的光滑半圆形轨道运动,PQ为半圆形轨道竖直的直径,g=10m/s2,下列说法正确的是( )
A.弹簧弹开过程,弹力对A的冲量与弹力对B的冲量相同
B.刚开始弹簧的弹性势能大小为2.0J
C.A球从P点运动到Q点过程中所受合外力的冲量大小为0.2N s
D.若使A球不能到达Q点,则半圆轨道半径的最小值为0.72m
二.多选题(共4小题)
(多选)9.(2024秋 长沙期末)如图甲所示,倾角为30°的光滑斜面(足够长)固定在水平面上,质量为2kg的物块静止在斜面底端,t=0时刻给物块施加沿斜面方向的作用力F,物块运动的a﹣t图像如图乙所示,取沿斜面向上为正方向,重力加速度g=10m/s2,下列说法中正确的有( )
A.前2s内F的大小是第3s的2倍
B.3s内物块所受合力的冲量为零
C.3s内力F做功为零
D.3s内力F的冲量为30N s
(多选)10.(2024秋 武昌区期末)如图甲所示,物块A和B叠放在水平地面上。敲击B,B立即获得水平向右的初速度v0,A、B都向右运动,A始终没有从B上滑落,最终两物块都运动至停下来。这段过程中,B的v﹣t关系图线如图乙所示,已知A与B、B与地面间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.物块A和B的质量相等
B.A与B左端的距离至少为
C.摩擦力对A、B的总冲量大小之比为1:3
D.A和B间因摩擦产生的热量与B和地面间产生热量之比是1:3
(多选)11.(2024秋 开福区校级期末)如图所示,在光滑的水平杆上套有一个质量为m的滑环。滑环上通过一根不可伸缩的轻绳悬挂着一个质量为M的物块(可视为质点),绳长为L。将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆;若滑环不固定时,仍给物块以同样的水平冲量,则(g为重力加速度)( )
A.给物块的水平冲量为2M
B.物块上升的最大高度为
C.物块上升最高时的速度为
D.物块在最低点时对细绳的拉力3Mg
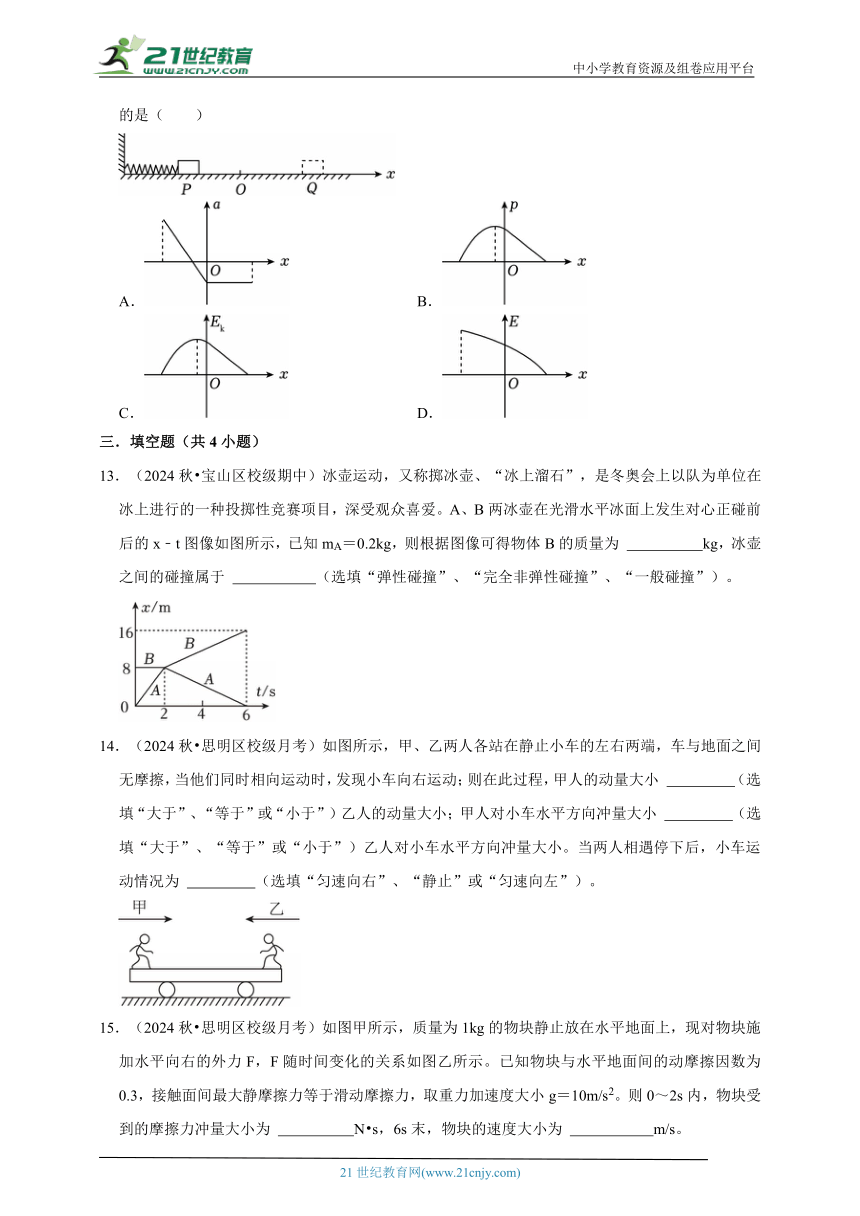
(多选)12.(2024秋 南开区校级期末)一弹射机构的简化模型如图所示,一理想轻质弹簧左端固定在墙上,处于原长时右端到达水平面上的O点。一滑块将弹簧右端压缩到P点,滑块与弹簧没有拴接。静止释放后,弹簧把滑块弹开,滑块运动到O点右侧的Q点停下,已知滑块与水平面间的动摩擦因数处处相同。以O点为坐标原点,水平向右为正方向建立x轴。整个过程滑块的加速度a、动量p、动能Ek及滑块与弹簧组成的系统的机械能E随位置坐标x的变化规律,符合实际的是( )
A. B.
C. D.
三.填空题(共4小题)
13.(2024秋 宝山区校级期中)冰壶运动,又称掷冰壶、“冰上溜石”,是冬奥会上以队为单位在冰上进行的一种投掷性竞赛项目,深受观众喜爱。A、B两冰壶在光滑水平冰面上发生对心正碰前后的x﹣t图像如图所示,已知mA=0.2kg,则根据图像可得物体B的质量为 kg,冰壶之间的碰撞属于 (选填“弹性碰撞”、“完全非弹性碰撞”、“一般碰撞”)。
14.(2024秋 思明区校级月考)如图所示,甲、乙两人各站在静止小车的左右两端,车与地面之间无摩擦,当他们同时相向运动时,发现小车向右运动;则在此过程,甲人的动量大小 (选填“大于”、“等于”或“小于”)乙人的动量大小;甲人对小车水平方向冲量大小 (选填“大于”、“等于”或“小于”)乙人对小车水平方向冲量大小。当两人相遇停下后,小车运动情况为 (选填“匀速向右”、“静止”或“匀速向左”)。
15.(2024秋 思明区校级月考)如图甲所示,质量为1kg的物块静止放在水平地面上,现对物块施加水平向右的外力F,F随时间变化的关系如图乙所示。已知物块与水平地面间的动摩擦因数为0.3,接触面间最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2。则0~2s内,物块受到的摩擦力冲量大小为 N s,6s末,物块的速度大小为 m/s。
16.(2023秋 金台区期末)质量是10g的子弹,以300m/s的速度射入质量是240g、静止在光滑水平桌面上的木块。
(1)如果子弹留在木块中,木块运动的速度是 m/s;
(2)如果子弹把木块打穿,子弹穿过后的速度为100m/s,这时木块的速度又是 m/s。(结果保留两位有效数字)
四.解答题(共4小题)
17.(2024秋 苏州期末)如图所示,P为固定挡板,质量为2m的长木板A以水平初速度v0沿光滑水平面向右运动。某时刻质量为m的小物块B轻轻释放到A的右端,第一次达到共同速度后,B与P发生碰撞,一段时间后B与A第二次达到共同速度,之后B与P发生了多次碰撞,B始终未从A上滑落。已知A、B间的动摩擦因数为μ,重力加速度为g,B与P发生碰撞时无机械能损失且碰撞时间极短。求:
(1)A、B第一次的共同速度大小v1;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功W;
(3)A的最小长度L。
18.(2024秋 盐城期末)高空坠物极易对行人造成伤害。《中华人民共和国民法典》第一千二百五十四条规定:禁止从建筑物中抛掷物品。从建筑物中抛掷物品或者从建筑物上坠落的物品造成他人损害的,由侵权人依法承担侵权责任。若一个50g的生鸡蛋从居民楼的7楼阳台坠下,距离地面的高度大约20m,与地面的撞击时间约为0.01s。(g取10m/s2)求:
(1)鸡蛋着地前瞬间的速度大小;
(2)该鸡蛋着地过程中对地面产生的平均冲击力。
19.(2024秋 雨花区校级期末)如图所示,倾角θ=37°的斜面AB与长度为L=0.6m的水平面BC在B点衔接,衔接点平滑,质量为m=1kg的可视为质点的滑块Q静置在水平面的右端C。可视为质点的滑块P自斜面上高h=0.3m处静止释放,与滑块Q发生弹性碰撞后,滑块Q在C点立即进入光滑竖直半圆轨道DE的内侧(CD间隙不计),D为圆的最高点,圆半径记为R。滑块Q经圆弧后在E点水平抛出,最终落于水平地面FG上,水平面FG与BC的高度差为H=1.2m。已知滑块P与AB面和BC面的动摩擦因数都为μ=0.1。
(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①求滑块Q进入D点时的速度vD。
②求半圆轨道的半径R的取值范围。
③求滑块Q离开E后落在FG面上的最大射程。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,求滑块Q进入D点时对D的压力大小的范围。
20.(2024秋 无锡期末)如图所示,小车上固定有处于竖直平面内的特殊形状的光滑圆管,其中AB段圆弧所对应的半径R1=0.5m,圆心角∠AOB=53°,BC段对应的半径R2=0.35m,是四分之一圆弧,B点切线方向竖直,C点与小车表面平滑衔接,小车CD部分与小球之间的动摩擦因数μ=0.4。质量M=2kg的小车(含圆管)静止放置于光滑的水平地面上,现将质量m=2kg的小球由A点左上方某点以v0=4m/s的初速度水平抛出,使小球刚好可以无碰撞的进入到圆管中。小球穿过圆管后,滑上CD段。不计空气阻力,取g=10m/s2,sin53°=0.8,cos53°=0.6,求:
(1)小球从抛出点到A点竖直高度;
(2)小球刚运动到C点时,小车的速度大小;
(3)要使小球不从车上落下,则CD长度至少是多少?
高考物理高频易错押题预测 动量与动量守恒定律
参考答案与试题解析
一.选择题(共8小题)
1.(2025 庐阳区校级模拟)图为丁俊晖正在准备击球,设丁俊晖在某一杆击球过程中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球A的动量pA=5kg m/s,花色球B静止,碰后花色球B的动量变为P'B=4kg m/s,则两球质量mA与mB间的关系可能是( )
A. B. C.mB=2mA D.mB=5mA
【考点】动量守恒与能量守恒共同解决实际问题;用能量守恒定律解决实际问题.
【专题】应用题;信息给予题;定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】C
【分析】由动量守恒定律,结合弹性碰撞与完全非弹性碰撞两种临界条件,分析碰撞的过程后可能的运动的情况即可。
【解答】解:碰撞过程系统动量守恒,以白色球的初速度方向为正方向,由动量守恒定律得:
pA=pA′+pB′
代入数据得:5kg m/s=pA′+4kg m/s
解得:pA′=1kg m/s,方向与白色球的初速度方向相同。
若碰撞后二者的速度相等(设为v共),则有:
mAv共=pA′=1kg m/s,mBv共=pB′=4kg m/s
联立可得:mB=4mA
若碰撞过程系统的机械能不变,根据碰撞过程总动能不增加,则有:
解得
碰后两球同向运动,A的速度不大于B的速度,则
解得mB≤4mA
综上可知
故C正确,ABD错误。
故选:C。
【点评】该题考查动量守恒定律以及碰撞的特点,考虑弹性碰撞与完全非弹性碰撞,即可求出可能的质量关
2.(2024秋 南京期末)如图所示,在离地面高为h处将质量为m的小球以初速度v0水平抛出,重力加速度为g,不计空气阻力。下列说法正确的是( )
A.落地前瞬间,小球的动量大小为
B.从抛出到落地,小球所受重力的冲量大小为
C.从抛出到落地,小球动量的变化量方向竖直向上
D.从抛出到落地,小球动量的变化量大小为
【考点】动量定理的内容和应用;平抛运动速度的计算;用动量的定义式计算物体的动量.
【专题】定量思想;推理法;动量定理应用专题;理解能力.
【答案】D
【分析】根据动能定理求解落地时速度大小,再根据动量的计算公式求解落地时物体动量大小;根据运动学公式求落地时间,根据冲量公式求冲量,根据动量定理求解动量变化量。
【解答】解:A、由动能定理
得
动量为
故A错误;
B、由,重力的冲量大小为
故B错误;
CD、合力的冲量等于动量的变化量,由动量定理有
则小球动量的变化量方向竖直向下,其大小为,故C错误,D正确。
故选:D。
【点评】本题主要是考查动量定理,利用动量定理解答问题时,要注意分析运动过程中物体的受力情况,知道合外力的冲量才等于动量的变化。
3.(2024秋 扬州期末)骑电瓶车必须戴好头盔。在头部受到撞击时,其他条件相同,戴头盔与不戴头盔相比,骑行者头部( )
A.动量变化小 B.动量变化慢
C.受到撞击力大 D.受到撞击力的冲量大
【考点】动量定理的内容和应用.
【专题】定性思想;推理法;动量定理应用专题;理解能力.
【答案】B
【分析】骑行者头部的动量的变化量是一定的,再根据动量定理分析。
【解答】解:根据动量定理 I=FΔt=Δp,可得,由于气囊的缓冲与头部的撞击时间Δt延长了,从而减小了对头部的作用力F,也即减小了驾驶员头部撞击过程中的动量变化快慢,但驾驶员头部撞击过程中动量变化量和撞击力的冲量I并未改变,故B正确,ACD错误。
故选:B。
【点评】本题考查了动量定理在实际生活中的应用,要注意明确头盔增加了冲击时间,从而减小了冲击力。
4.(2024秋 徐州期末)做自由落体运动的物体,其动量p与时间t的p﹣t关系图线为( )
A. B.
C. D.
【考点】动量定理的内容和应用;自由落体运动的规律及应用.
【专题】定性思想;推理法;动量定理应用专题;理解能力.
【答案】B
【分析】明确自由落体的物体只受重力,加速度恒定不变,速度和时间成正比,再由动量的表达式分析即可。
【解答】解:自由落体运动的加速度是恒定不变的,由v=at可知,物体的速度与时间成正比,由p=mv=mat,可知动量与时间成正比,故B正确,ACD错误;
故选:B。
【点评】本题考查图象以及自由落体运动的规律,要注意掌握用图象来描述物体的运动性质的方法。
5.(2024秋 郴州期末)三个完全相同的小球,质量均为m,其中小球A、B固定在竖直轻杆的两端,A球紧贴竖直光滑墙面,B球位于足够大的光滑水平地面上,小球C紧贴小球B,如图所示,三小球均保持静止。某时,小球A受到轻微扰动开始顺着墙面下滑,直至小球A落地前瞬间的运动过程中,三小球始终在同一竖直面上。已知小球C的最大速度为v,轻杆长为L,重力加速度为g,下列关于该过程的说法中正确的是( )
A.A、B、C三球组成的系统动量守恒
B.竖直墙对小球A的冲量大小为3mv
C.小球A落地前瞬间,动能大小为
D.小球A落地前瞬间,小球C的速度是小球B速度的2倍
【考点】动量守恒定律的内容、条件和判断;多物体系统的机械能守恒问题.
【专题】定量思想;推理法;动量与动能定理或能的转化与守恒定律综合;推理论证能力.
【答案】C
【分析】分析小球的运动特点和运动过程中的临界状态;根据动量守恒定律和几何关系得出小球的速度关系,结合能量关系完成分析。
【解答】解:A、A、B、C三球组成的系统在水平方向合外力不为零,受墙的推力,竖直方向合外力也不为零,故动量不守恒,故A错误;
B、B和C分离后小球C做匀速直线运动,所以B、C分离时,两球速度均为v,对三小球整体列水平方向动量定理,则墙对小球A的冲量I=2mv,故B错误;
C、轻杆对小球A做功大小等于对小球B做功大小,即等于小球B、C的动能增量,则,小球A落地前瞬间动能大小为EkA=mgL﹣W,解得,故C正确;
D、自小球A离开墙面到小球落地,A、B组成的系统水平方向动量守恒,规定向右为正方向,则mv=mvB+mvAx且有vB=vAx解得,小球C的速度是小球A水平速度的2倍,但小球A有竖直速度分量,故D错误。
故选:C。
【点评】本题主要考查了动量守恒定律的相关应用,理解动量守恒的条件,结合能量守恒定律和关联速度的特点即可完成分析。
6.(2024秋 徐州期末)为确保公共安全,市民遛狗时应牵绳。如图所示,一市民遛狗时匀速前行,已知绳中拉力大小为F、方向与水平面夹角为θ。则在t时间内拉力的冲量为( )
A.0
B.Ft,方向与F方向一致
C.Ftcosθ,方向与F方向一致
D.Ftcosθ,方向沿水平方向向左
【考点】求恒力的冲量.
【专题】定量思想;控制变量法;动量定理应用专题;理解能力.
【答案】B
【分析】根据冲量公式进行计算。
【解答】解:根据冲量公式可得
I=Ft
方向与F方向相同,故B正确,ACD错误。
故选:B。
【点评】本题考查的是恒力做功,直接利用公式求解,题型简单。
7.(2024秋 扬州期末)如图所示,在水平桌面上,粘在一起的两个一元硬币甲与静止的一元硬币乙发生一维碰撞。在下列描述甲、乙速度v与时间t的关系图像中,可能正确的是( )
A. B.
C. D.
【考点】分析碰撞的合理性.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】A
【分析】根据动量守恒定律结合图像斜率的意义分析。
【解答】解:硬币与桌面的动摩擦因数相同,根据μmg=ma
可知a=μg
则图像的斜率应相同;
规定向右为正方向,根据动量守恒定律有2mv0=2mv1+mv2
图像中每个单位格设为1,代入验证可知A符合,故A正确,BCD错误;
故选:A。
【点评】本题考查动量守恒定律,解题关键掌握图像的认识,注意动量守恒的条件。
8.(2024秋 南京期末)如图所示,在光滑的水平桌面上有体积相同的两个小球A、B,质量分别为m=0.1kg和M=0.3kg,两球中间夹着一根压缩的轻弹簧,原来处于静止状态,同时放开A、B球和弹簧,已知A球脱离弹簧的速度为6m/s,接着A球进入与水平面相切,半径为0.5m的竖直面内的光滑半圆形轨道运动,PQ为半圆形轨道竖直的直径,g=10m/s2,下列说法正确的是( )
A.弹簧弹开过程,弹力对A的冲量与弹力对B的冲量相同
B.刚开始弹簧的弹性势能大小为2.0J
C.A球从P点运动到Q点过程中所受合外力的冲量大小为0.2N s
D.若使A球不能到达Q点,则半圆轨道半径的最小值为0.72m
【考点】动量守恒与能量守恒共同解决实际问题;绳球类模型及其临界条件;动能定理的简单应用;动量定理的内容和应用.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】D
【分析】根据弹簧对A、B的弹力关系、作用时间关系分析弹力对A、B冲量大小关系;弹簧弹开过程,根据动量守恒定律求A球脱离弹簧时A、B球获得的速度,根据能量守恒定律计算最大弹性势能;由机械能守恒定律求A球到达Q点的速度,再由动量定理求A球从P点运动到Q点过程中所受合外力的冲量大小;在最高点根据牛顿第二定律结合机械能守恒定律解答。
【解答】解:A.弹簧弹开过程,弹簧对A、B的弹力大小相等、方向相反、作用时间相等,由I=Ft可知,弹力对A、B的冲量大小相等,方向相反,故A错误;
B.释放弹簧过程中,A、B系统动量守恒,设A球脱离弹簧时A、B的速度大小分别为v1、v2,以向右为正方向,由动量守恒定律得:mv1﹣Mv2=0
由题知:v1=6m/s
解得:v2=2m/s
根据机械能守恒定律可得,刚开始弹簧的弹性势能大小为:
解得:Ep=2.4J,故B错误;
C.设A球至Q点的速度大小为vQ,A球从P点运动到Q点过程中只有重力做功,机械能守恒,取水平桌面为零势能面,由机械能守恒定律得:mg 2R
解得:vQ=4m/s
小球A从P点运动到Q点过程中,取水平向左为正方向,
由动量定理可知,A球从P点运动到Q点过程中所受合外力的冲量大小为:IA=mvQ﹣m(﹣v1)=m(vQ+v1)=0.1×(4+6)N s=1N s,故C错误;
D.A球恰能到达最高点时有mg
A球从最低点到最高点有﹣mg×2R
解得R=0.72m
则若使A球不能到达Q点,则半圆轨道半径的最小值为0.72m,故D正确;
故选:D。
【点评】本题主要是考查了动量守恒定律和机械能守恒定律;对于动量守恒定律,其守恒条件是:系统不受外力作用或合外力为零;解答时要首先确定一个正方向,利用碰撞前系统的动量和碰撞后系统的动量相等列方程求解。
二.多选题(共4小题)
(多选)9.(2024秋 长沙期末)如图甲所示,倾角为30°的光滑斜面(足够长)固定在水平面上,质量为2kg的物块静止在斜面底端,t=0时刻给物块施加沿斜面方向的作用力F,物块运动的a﹣t图像如图乙所示,取沿斜面向上为正方向,重力加速度g=10m/s2,下列说法中正确的有( )
A.前2s内F的大小是第3s的2倍
B.3s内物块所受合力的冲量为零
C.3s内力F做功为零
D.3s内力F的冲量为30N s
【考点】动量定理的内容和应用;重力做功的特点和计算;动能定理的简单应用.
【专题】定量思想;推理法;动量定理应用专题;推理论证能力.
【答案】ABD
【分析】根据牛顿第二定律求解外力,再根据运动学公式求解位移,再求出拉力做的功;根据冲量的计算公式求解冲量。
【解答】解:A、0~2s内,根据牛顿第二定律得:F1﹣mgsin30°=ma1,得:F1=20N
在2~3s内,根据牛顿第二定律得:F2+mgsin 30°=ma2,得:F2=10N
则前2s内F的大小是第3s的2倍,故A正确;
B、图像与坐标轴围成的面积代表合力的冲量;3s内物块所受合力的冲量为I=(5×2﹣10×1)N s=0,故B正确;
C、0~2s内,物体的位移为x1m=10m,2~3s内,物体的位移为x2m=5m
所以3s内力F做功为W=F1x1﹣F2x2=20×10J+10×5J=150J,故C错误;
D、设F1的方向为正方向,根据冲量的计算公式可知3s内力F的冲量为IF=F1t1﹣F2t2=20×2N s﹣10×1N s=30N s,故D正确;
故选:ABD。
【点评】本题主要是考查牛顿运动定律的综合应用、功的计算以及冲量的计算等,能够根据图象分析受力情况,再结合运动学公式、功的计算公式求解是关键。
(多选)10.(2024秋 武昌区期末)如图甲所示,物块A和B叠放在水平地面上。敲击B,B立即获得水平向右的初速度v0,A、B都向右运动,A始终没有从B上滑落,最终两物块都运动至停下来。这段过程中,B的v﹣t关系图线如图乙所示,已知A与B、B与地面间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.物块A和B的质量相等
B.A与B左端的距离至少为
C.摩擦力对A、B的总冲量大小之比为1:3
D.A和B间因摩擦产生的热量与B和地面间产生热量之比是1:3
【考点】动量定理的内容和应用;有外力的水平板块模型;常见力做功与相应的能量转化;求变力的冲量.
【专题】定量思想;推理法;动量定理应用专题;功能关系 能量守恒定律;推理论证能力.
【答案】AD
【分析】根据图像得到A、B的加速度,然后根据牛顿第二定律得到它们的质量关系;根据动量定理得到它们的动量变化关系;根据平均速度得到它们的位移,然后可得它们的相对位移;根据摩擦力与相对位移的乘积分别得到A和B、B和地面之间因摩擦产生的热量。
【解答】解:A、设A的质量为mA,B的质量为mB,动摩擦因数大小为μ,根据图像可知B的加速度大小为aB,,对A根据牛顿第二定律有μmAg=mAaA,对B根据牛顿第二定律有μmAg+μ(mA+mB)g=mBaB,联立解得mA=mB,故A正确;
C、A的初速度为零,最后和B静止在地面上,根据动量定理可知摩擦力对A的冲量大小为0,摩擦力对B的冲量大小为mBv0,故C错误;
B、开始时A加速,B减速运动,当A、B速度相等后一起减速运动,所以A与B左端的距离至少为,解得,故B错误;
D、A和B间因摩擦产生的热量为Q=μmAgΔx,B与地面之间因摩擦产生的热量为Q',整理得Q',则Q:Q'=1:3,故D正确。
故选:AD。
【点评】本题考查了动量定理、牛顿第二定律和功能关系相关内容,综合性较强。
(多选)11.(2024秋 开福区校级期末)如图所示,在光滑的水平杆上套有一个质量为m的滑环。滑环上通过一根不可伸缩的轻绳悬挂着一个质量为M的物块(可视为质点),绳长为L。将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆;若滑环不固定时,仍给物块以同样的水平冲量,则(g为重力加速度)( )
A.给物块的水平冲量为2M
B.物块上升的最大高度为
C.物块上升最高时的速度为
D.物块在最低点时对细绳的拉力3Mg
【考点】动量守恒与能量守恒共同解决实际问题;牛顿第二定律与向心力结合解决问题;机械能守恒定律的简单应用;动量定理的内容和应用;某一方向上的动量守恒问题.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】BD
【分析】A.将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆,根据机械能守恒定律、冲量的计算公式分别列式,即可分析判断;
BC.滑环不固定时,物块和滑环组成的系统机械能守恒,水平方向动量守恒,据此列式,即可分析判断;
D.结合前面分析,由牛顿第二定律列式,即可分析判断。
【解答】解:A.设物块初速度大小为v0,
将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆,根据机械能守恒定律可得:,
解得:,
故给物块的水平冲量大小为:,故A错误;
BC.滑环不固定时,物块初速度大小仍为v0,设物块摆至最大高度h时,滑块与物块速度大小都为v,
在此过程中物块和滑环组成的系统机械能守恒,水平方向动量守恒,以物块初速度的方向为正方向,
由该系统水平方向动量守恒可得:Mv0=(m+M)v,
由该系统机械能守恒可得:,
联立可得:,,故B正确,C错误;
D.对m、M组成的系统,当M第一次回到最低点时,由该系统水平方向动量守恒和能量守恒可知,m、M的相对速度大小仍然为v0,
则在最低点,由牛顿第二定律可知:T,
解得:T=3Mg,故D正确;
故选:BD。
【点评】本题主要考查动量守恒与能量守恒共同解决实际问题,解题时需注意挖掘临界条件:在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,即速度相等或位移相等时。
(多选)12.(2024秋 南开区校级期末)一弹射机构的简化模型如图所示,一理想轻质弹簧左端固定在墙上,处于原长时右端到达水平面上的O点。一滑块将弹簧右端压缩到P点,滑块与弹簧没有拴接。静止释放后,弹簧把滑块弹开,滑块运动到O点右侧的Q点停下,已知滑块与水平面间的动摩擦因数处处相同。以O点为坐标原点,水平向右为正方向建立x轴。整个过程滑块的加速度a、动量p、动能Ek及滑块与弹簧组成的系统的机械能E随位置坐标x的变化规律,符合实际的是( )
A. B.
C. D.
【考点】动量定理的内容和应用;动能定理的简单应用;常见力做功与相应的能量转化.
【专题】定性思想;推理法;动量和能量的综合;推理论证能力.
【答案】AC
【分析】根据各个物理量的表达式得到对应物理量与x的函数关系式,根据函数关系式判断图像是否正确。
【解答】解:A.当滑块在O点左侧位置坐标为x时,弹簧压缩量为x,设滑块的质量为m,弹簧的劲度系数为k,滑块与水平面间的动摩擦因数为μ,由牛顿第二定律,有﹣kx﹣μmg=ma
得
当滑块在O点右侧时,有﹣μmg=ma
得a=﹣μga﹣x图像为两段直线,故A正确。
B.取一段位移微元Δx,可认为滑块的加速度不变,设为a,速度为v,有
设滑块运动到N处时弹簧弹力等于摩擦力,加速度为0,由P到N,加速度逐渐减小,速度逐渐增大,逐渐减小,p﹣x图线的斜率逐渐减小;到N处时p﹣x图线的斜率减为0;由N到O,加速度反向逐渐增大,速度逐渐减小,绝对值逐渐增大,p﹣x图线的斜率绝对值逐渐增大;由O到Q,加速度不变,速度逐渐减小,绝对值逐渐增大,p﹣x图线的斜率绝对值逐渐增大,p﹣x图像O点右侧不可能为倾斜的直线,故B错误。
C.滑块移动位移微元Δx,由动能定理有
F合Δx=ΔEk
可得
,Ek﹣x图像由P到N斜率减小,由N到O斜率绝对值增大,O点右侧斜率不变,为倾斜的直线,故C正确。
D.由能量转化可知,滑块克服摩擦力做的功等于系统机械能的减少量。对一段位移微元Δx,有﹣μmgΔx=ΔE
可知
即E﹣x图像为斜率不变的倾斜的直线,故D错误。
故选:AC。
【点评】通过斜率变化判断图像是否正确是本题解题关键。
三.填空题(共4小题)
13.(2024秋 宝山区校级期中)冰壶运动,又称掷冰壶、“冰上溜石”,是冬奥会上以队为单位在冰上进行的一种投掷性竞赛项目,深受观众喜爱。A、B两冰壶在光滑水平冰面上发生对心正碰前后的x﹣t图像如图所示,已知mA=0.2kg,则根据图像可得物体B的质量为 0.6 kg,冰壶之间的碰撞属于 弹性碰撞 (选填“弹性碰撞”、“完全非弹性碰撞”、“一般碰撞”)。
【考点】用动量守恒定律解决简单的碰撞问题;利用x﹣t图像的斜率求解物体运动的速度.
【专题】定量思想;推理法;动量与动能定理或能的转化与守恒定律综合;分析综合能力.
【答案】0.6,弹性碰撞。
【分析】根据x﹣t图线斜率求速度,根据动量守恒定律求质量,然后计算碰撞前后的机械能总量关系,即可解答。
【解答】解:x﹣t图线的斜率表示速度,则碰撞前,有,vB=0
碰撞后,m/s=﹣2m/s,m/s=2m/s
以碰撞前A的方向为正方向,由动量守恒定律可知
mAvA+mBvB=mAvA′+mBvB′
代入数据解得mB=0.6kg
碰撞前总动能为1.6J
碰撞后总动能为EK′mAvA′2mBvB′2
代入数据解得EK′=1.6J
碰撞前后重力势能不变,则碰撞前后机械能守恒,两冰壶发生的是弹性碰撞。
故答案为:0.6,弹性碰撞。
【点评】本题是一道综合题,需要学生根据x﹣t图线求速度,再判断机械能,难度中等。
14.(2024秋 思明区校级月考)如图所示,甲、乙两人各站在静止小车的左右两端,车与地面之间无摩擦,当他们同时相向运动时,发现小车向右运动;则在此过程,甲人的动量大小 小于 (选填“大于”、“等于”或“小于”)乙人的动量大小;甲人对小车水平方向冲量大小 小于 (选填“大于”、“等于”或“小于”)乙人对小车水平方向冲量大小。当两人相遇停下后,小车运动情况为 静止 (选填“匀速向右”、“静止”或“匀速向左”)。
【考点】动量守恒定律的一般应用.
【专题】应用题;定量思想;推理法;动量和能量的综合;分析综合能力.
【答案】小于;小于;静止。
【分析】甲、乙两人相向而行的过程中,甲、乙两人及小车组成的系统在水平方向所受的合外力为零,系统动量守恒,根据动量守恒定律列式分析即可。
【解答】解:甲、乙两人相向而行的过程中,甲、乙两人及小车组成的系统在水平方向所受的合外力为零,系统动量守恒,
以向右为正方向,在水平方向,根据动量守恒定律得:m甲v甲+m乙v乙+m车v车=0
小车向右运动,小车的动量方向向右,说明甲与乙两人的总动量向左,因乙向左运动,甲向右运动,则甲的动量必定小于乙的动量;
小车向右运动,对小车,由动量定理可知,小车受外力的冲量向右,人在行走时对小车的作用力冲量与人的运动方向相反,则说明乙对小车的作用力冲量大于甲对小车的作用力冲量;
两人与车组成的系统动量守恒,系统初状态动量为零,当两人都停下后两人的动量都为零,由动量守恒定律可知,小车的动量也为零,小车静止。
故答案为:小于;小于;静止。
【点评】本题考查动量守恒定律和动量定理的直接应用,关键要掌握动量守恒的条件:合外力为零,要注意速度和动量的矢量性。
15.(2024秋 思明区校级月考)如图甲所示,质量为1kg的物块静止放在水平地面上,现对物块施加水平向右的外力F,F随时间变化的关系如图乙所示。已知物块与水平地面间的动摩擦因数为0.3,接触面间最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2。则0~2s内,物块受到的摩擦力冲量大小为 4.5 N s,6s末,物块的速度大小为 13.5 m/s。
【考点】F﹣t图像中的动量问题;求恒力的冲量;用动量定理求平均作用力.
【专题】定量思想;推理法;动量定理应用专题;推理论证能力.
【答案】4.5;13.5。
【分析】根据题意求最大静摩擦力,再结合图像分析运动情况,由冲量的概念、动量定理等列式代入数据计算。
【解答】解:物块与水平地面间的最大静摩擦力为fmax=μmg=0.3×1×10N=3N
由F﹣t图像可知,在0~1s内物块受到静摩擦力作用,则0~2s内,物块受到的摩擦力冲量大小为
在t=1s时物块开始运动,则1~6s内,对物块根据动量定理可得I合=IF﹣If=mv﹣0
其中;If=3×5N s=15N s
代入数据解得6s末物块的速度大小v=13.5m/s。
故答案为:4.5;13.5。
【点评】本题主要考查F﹣t图像中的动量问题,解题时需注意,F﹣t图像与坐标轴所围面积,表示该力冲量。
16.(2023秋 金台区期末)质量是10g的子弹,以300m/s的速度射入质量是240g、静止在光滑水平桌面上的木块。
(1)如果子弹留在木块中,木块运动的速度是 12 m/s;
(2)如果子弹把木块打穿,子弹穿过后的速度为100m/s,这时木块的速度又是 8.3 m/s。(结果保留两位有效数字)
【考点】动量守恒定律在子弹打物块模型中的应用.
【专题】定量思想;寻找守恒量法;动量定理应用专题;分析综合能力.
【答案】(1)12;(2)8.3。
【分析】(1)(2)子弹射入木块的过程和打穿木块的过程,分别根据动量守恒定律求解木块运动的速度。
【解答】解:(1)取子弹的初速度方向为正方向,根据动量守恒定律有
m1v0=(m1+m2)v共
解得
v共=12m/s
则子弹留在木块中,木块运动的速度是12m/s;
(2)取子弹的初速度方向为正方向,根据动量守恒定律有
m1v0=m1v1+m2v2
解得木块的速度为
v2≈8.3m/s
故答案为:(1)12;(2)8.3。
【点评】对于子弹打木块的过程,要掌握其基本规律是动量守恒定律,要明确规定正方向,用正负号表示速度方向。
四.解答题(共4小题)
17.(2024秋 苏州期末)如图所示,P为固定挡板,质量为2m的长木板A以水平初速度v0沿光滑水平面向右运动。某时刻质量为m的小物块B轻轻释放到A的右端,第一次达到共同速度后,B与P发生碰撞,一段时间后B与A第二次达到共同速度,之后B与P发生了多次碰撞,B始终未从A上滑落。已知A、B间的动摩擦因数为μ,重力加速度为g,B与P发生碰撞时无机械能损失且碰撞时间极短。求:
(1)A、B第一次的共同速度大小v1;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功W;
(3)A的最小长度L。
【考点】动量守恒定律在板块模型中的应用;常见力做功与相应的能量转化.
【专题】定量思想;推理法;动量与动能定理或能的转化与守恒定律综合;推理论证能力.
【答案】(1)A、B第一次的共同速度大小为v0;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功为;
(3)A的最小长度为。
【分析】(1)根据动量守恒定律分析解答;
(2)根据动量守恒定律结合动能定理分析解答;
(3)整个过程中,B相对于A一直向左运动,最终两者速度都为零,根据能量守恒定律解答。
【解答】解:(1)从B滑上A到第一次达到共同速度v1,规定向右为正方向,根据系统动量守恒有
2mv0=(m+2m)v1
得v1v0
(2)从第一次碰撞后到第二次达到共同速度v2,取向右为正方向,根据系统动量守恒有
2mv1﹣mv1=3mv2
得v2v1v0
从开始到第二次达到共同速度过程中,对A运用动能定理
W22
得B对A做的功W
(3)整个过程中,B相对于A一直向左运动,最终两者速度都为零
设两者相对运动的距离为x,A、B系统能量守恒
2μmgx
得x
则为使整个运动过程中B不从A上滑落,A的最小长度L=x
答:(1)A、B第一次的共同速度大小为v0;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功为;
(3)A的最小长度为。
【点评】本题主要是考查动量守恒定律和能量守恒定律;解答时要首先确定一个正方向,利用碰撞前系统的动量和碰撞后系统的动量相等列方程,再根据能量关系列方程求解。
18.(2024秋 盐城期末)高空坠物极易对行人造成伤害。《中华人民共和国民法典》第一千二百五十四条规定:禁止从建筑物中抛掷物品。从建筑物中抛掷物品或者从建筑物上坠落的物品造成他人损害的,由侵权人依法承担侵权责任。若一个50g的生鸡蛋从居民楼的7楼阳台坠下,距离地面的高度大约20m,与地面的撞击时间约为0.01s。(g取10m/s2)求:
(1)鸡蛋着地前瞬间的速度大小;
(2)该鸡蛋着地过程中对地面产生的平均冲击力。
【考点】动量定理的内容和应用;自由落体运动的规律及应用;牛顿第三定律的理解与应用.
【专题】定量思想;推理法;动量定理应用专题;理解能力.
【答案】(1)鸡蛋着地前瞬间的速度大小为20m/s;
(2)该鸡蛋着地过程中对地面产生的平均冲击力为100.5N。
【分析】(1)根据鸡蛋下落的总高度,计算鸡蛋落地时速度大小;
(2)再根据动量定理列方程求解地面对鸡蛋的冲击力,从而得到鸡蛋对地面产生的冲击力。
【解答】解:(1)鸡蛋下落过程有
v2=2gh
可得鸡蛋落地时速度为
v=20m/s
(2)鸡蛋与地面的撞击过程,取竖直向下为正方向,根据动量定理有
(mg﹣F)t=0﹣mν
代入数据得
F=100.5N
根据牛顿第三定律可知,该鸡蛋对地面产生的冲击力约为100.5N。
答:(1)鸡蛋着地前瞬间的速度大小为20m/s;
(2)该鸡蛋着地过程中对地面产生的平均冲击力为100.5N。
【点评】本题主要考查动量定理,利用动量定理解答问题时,要注意灵活选择研究过程,分析运动过程中物体的受力情况,规定正方向,用正负号表示矢量的方向。
19.(2024秋 雨花区校级期末)如图所示,倾角θ=37°的斜面AB与长度为L=0.6m的水平面BC在B点衔接,衔接点平滑,质量为m=1kg的可视为质点的滑块Q静置在水平面的右端C。可视为质点的滑块P自斜面上高h=0.3m处静止释放,与滑块Q发生弹性碰撞后,滑块Q在C点立即进入光滑竖直半圆轨道DE的内侧(CD间隙不计),D为圆的最高点,圆半径记为R。滑块Q经圆弧后在E点水平抛出,最终落于水平地面FG上,水平面FG与BC的高度差为H=1.2m。已知滑块P与AB面和BC面的动摩擦因数都为μ=0.1。
(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①求滑块Q进入D点时的速度vD。
②求半圆轨道的半径R的取值范围。
③求滑块Q离开E后落在FG面上的最大射程。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,求滑块Q进入D点时对D的压力大小的范围。
【考点】动量守恒与能量守恒共同解决实际问题;平抛运动速度的计算;绳球类模型及其临界条件;动能定理的简单应用.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①滑块Q进入D点时的速度vD大小为2m/s,方向水平向右;
②半圆轨道的半径R的取值范围为:0.2m≤R≤0.4m;
③滑块Q离开E后落在FG面上的最大射程为1.4m。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,滑块Q进入D点时对D的压力大小的范围为:0≤FN<30N。
【分析】(1)①滑块P从静止到C点,根据动能定理列式,滑块P与滑块Q碰撞时动量守恒、且碰撞过程无动能损失,据此列式,即可联立求解;
②在D点能够做圆周运动,根据牛顿第二定律可列式,D点到E点的过程,根据能量守恒定律列式,在E点,根据牛顿第二定律列式,即可联立求解;
③滑块自E点作平抛运动,则水平方向做匀速直线运动、竖直方向做自由落体运动,根据运动学规律列式,结合②及数学知识,即可分析求解。
(2)同(1)思路,由动能定理、弹性碰撞的性质、牛顿第二定律分别列式,即可分析求解。
【解答】解:(1)①滑块P从静止到C点,根据动能定理可得:
,
解得:
vC=2m/s,
滑块P与滑块Q碰撞时动量守恒,以水平向右为正方向,则有:
mvC=mvC'+mvD,
又因为是弹性碰撞,则碰撞过程无动能损失,有:
,
联立可得:
vD=2m/s,方向水平向右;
②在D点能够做圆周运动,根据牛顿第二定律可知:
,
解得:
R≤0.4m,
D点到E点的过程,根据能量守恒定律有:
,
在E点,根据牛顿第二定律有:
,
且:
FN≤70N,
联立得:
R≥0.2m,
所以R的取值范围为:
0.2m≤R≤0.4m;
③滑块自E点作平抛运动,水平方向做匀速直线运动,则射程为:
x=vEt,
竖直方向做自由落体运动,有:
,
结合②,联立可得:
,
有数学知识可得,当R=0.25m时,射程最大,
解得:xmax=1.4m;
(2)由动能定理有:
,
解得:
vC=2m/s,
滑块P与滑块Q碰撞时动量守恒,以水平向右为正方向,则有:
m1vC=m1v1+mv2,
又因为是弹性碰撞,则碰撞过程动能无损失,则有:
,
联立可得:
,
即:
,
则:
0<v2<2vC,
由牛顿第二定律可得:
,
解得:
0≤FN<30N;
答:(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①滑块Q进入D点时的速度vD大小为2m/s,方向水平向右;
②半圆轨道的半径R的取值范围为:0.2m≤R≤0.4m;
③滑块Q离开E后落在FG面上的最大射程为1.4m。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,滑块Q进入D点时对D的压力大小的范围为:0≤FN<30N。
【点评】本题主要考查动量守恒与能量守恒共同解决实际问题,解题时需注意挖掘临界条件:在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,即速度相等或位移相等时。
20.(2024秋 无锡期末)如图所示,小车上固定有处于竖直平面内的特殊形状的光滑圆管,其中AB段圆弧所对应的半径R1=0.5m,圆心角∠AOB=53°,BC段对应的半径R2=0.35m,是四分之一圆弧,B点切线方向竖直,C点与小车表面平滑衔接,小车CD部分与小球之间的动摩擦因数μ=0.4。质量M=2kg的小车(含圆管)静止放置于光滑的水平地面上,现将质量m=2kg的小球由A点左上方某点以v0=4m/s的初速度水平抛出,使小球刚好可以无碰撞的进入到圆管中。小球穿过圆管后,滑上CD段。不计空气阻力,取g=10m/s2,sin53°=0.8,cos53°=0.6,求:
(1)小球从抛出点到A点竖直高度;
(2)小球刚运动到C点时,小车的速度大小;
(3)要使小球不从车上落下,则CD长度至少是多少?
【考点】动量守恒与能量守恒共同解决实际问题;平抛运动速度的计算;机械能守恒定律的简单应用.
【专题】定量思想;推理法;力学综合性应用专题;推理论证能力.
【答案】(1)小球从抛出点到A点竖直高度为0.45m;
(2)小球刚运动到C点时,小车的速度大小为6m/s;
(3)要使小球不从车上落下,则CD长度至少是4m。
【分析】(1)小球进入到圆管之前做平抛运动,确定到达A点时速度方向与水平方向的夹角,以及在A点竖直分速度与水平分速度满足的关系,根据竖直方向做自由落体运动求解小球从抛出点到A点竖直高度。
(2)小球穿过圆管的过程,小球与小车组成的的系统在水平方向上动量守恒。根据动量守恒定律与机械能守恒定律求解小球刚运动到C点时,小车的速度大小。
(3)要使小球不从车上落下,CD长度最小时,小球与小车速度相同时,小球刚好滑动到D点。根据动量守恒定律与能量守恒定律解答。
【解答】解:(1)小球进入到圆管之前做平抛运动,到达A点时速度方向与水平方向的夹角为37°,在A点竖直分速度vy与水平分速度vx满足:
,其中:vx=v0=4m/s
解得:vy=3m/s
设小球从抛出点到A点竖直高度为h,由竖直方向做自由落体运动可得:
解得:h=0.45m
(2)小球穿过圆管的过程,小球与小车组成的的系统在水平方向上动量守恒。设小球刚运动到C点时小球的速度为v1,小车的速度为v2。以向右为正方向,根据动量守恒定律与机械能守恒定律分别得:
mv0=mv1+Mv2
解得:v1=﹣2m/s,v2=6m/s
(3)要使小球不从车上落下,CD长度最小(设为Lmin)时,小球与小车速度相同时,小球刚好滑动到D点。以向右为正方向,根据动量守恒定律与能量守恒定律分别得:
mv1+Mv2=(m+M)v共
解得:Lmin=4m
答:(1)小球从抛出点到A点竖直高度为0.45m;
(2)小球刚运动到C点时,小车的速度大小为6m/s;
(3)要使小球不从车上落下,则CD长度至少是4m。
【点评】本题考查了动量守恒定律与能量守恒定律的应用,考查了平抛运动的性质。要注意小球穿过圆管的过程,小球与小车组成的的系统只是在水平方向上满足动量守恒定律。掌握从动量与功能的角度处理问题的方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
高考物理高频易错押题预测 动量与动量守恒定律
一.选择题(共8小题)
1.(2025 庐阳区校级模拟)图为丁俊晖正在准备击球,设丁俊晖在某一杆击球过程中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球A的动量pA=5kg m/s,花色球B静止,碰后花色球B的动量变为P'B=4kg m/s,则两球质量mA与mB间的关系可能是( )
A. B. C.mB=2mA D.mB=5mA
2.(2024秋 南京期末)如图所示,在离地面高为h处将质量为m的小球以初速度v0水平抛出,重力加速度为g,不计空气阻力。下列说法正确的是( )
A.落地前瞬间,小球的动量大小为
B.从抛出到落地,小球所受重力的冲量大小为
C.从抛出到落地,小球动量的变化量方向竖直向上
D.从抛出到落地,小球动量的变化量大小为
3.(2024秋 扬州期末)骑电瓶车必须戴好头盔。在头部受到撞击时,其他条件相同,戴头盔与不戴头盔相比,骑行者头部( )
A.动量变化小 B.动量变化慢
C.受到撞击力大 D.受到撞击力的冲量大
4.(2024秋 徐州期末)做自由落体运动的物体,其动量p与时间t的p﹣t关系图线为( )
A. B.
C. D.
5.(2024秋 郴州期末)三个完全相同的小球,质量均为m,其中小球A、B固定在竖直轻杆的两端,A球紧贴竖直光滑墙面,B球位于足够大的光滑水平地面上,小球C紧贴小球B,如图所示,三小球均保持静止。某时,小球A受到轻微扰动开始顺着墙面下滑,直至小球A落地前瞬间的运动过程中,三小球始终在同一竖直面上。已知小球C的最大速度为v,轻杆长为L,重力加速度为g,下列关于该过程的说法中正确的是( )
A.A、B、C三球组成的系统动量守恒
B.竖直墙对小球A的冲量大小为3mv
C.小球A落地前瞬间,动能大小为
D.小球A落地前瞬间,小球C的速度是小球B速度的2倍
6.(2024秋 徐州期末)为确保公共安全,市民遛狗时应牵绳。如图所示,一市民遛狗时匀速前行,已知绳中拉力大小为F、方向与水平面夹角为θ。则在t时间内拉力的冲量为( )
A.0
B.Ft,方向与F方向一致
C.Ftcosθ,方向与F方向一致
D.Ftcosθ,方向沿水平方向向左
7.(2024秋 扬州期末)如图所示,在水平桌面上,粘在一起的两个一元硬币甲与静止的一元硬币乙发生一维碰撞。在下列描述甲、乙速度v与时间t的关系图像中,可能正确的是( )
A. B.
C. D.
8.(2024秋 南京期末)如图所示,在光滑的水平桌面上有体积相同的两个小球A、B,质量分别为m=0.1kg和M=0.3kg,两球中间夹着一根压缩的轻弹簧,原来处于静止状态,同时放开A、B球和弹簧,已知A球脱离弹簧的速度为6m/s,接着A球进入与水平面相切,半径为0.5m的竖直面内的光滑半圆形轨道运动,PQ为半圆形轨道竖直的直径,g=10m/s2,下列说法正确的是( )
A.弹簧弹开过程,弹力对A的冲量与弹力对B的冲量相同
B.刚开始弹簧的弹性势能大小为2.0J
C.A球从P点运动到Q点过程中所受合外力的冲量大小为0.2N s
D.若使A球不能到达Q点,则半圆轨道半径的最小值为0.72m
二.多选题(共4小题)
(多选)9.(2024秋 长沙期末)如图甲所示,倾角为30°的光滑斜面(足够长)固定在水平面上,质量为2kg的物块静止在斜面底端,t=0时刻给物块施加沿斜面方向的作用力F,物块运动的a﹣t图像如图乙所示,取沿斜面向上为正方向,重力加速度g=10m/s2,下列说法中正确的有( )
A.前2s内F的大小是第3s的2倍
B.3s内物块所受合力的冲量为零
C.3s内力F做功为零
D.3s内力F的冲量为30N s
(多选)10.(2024秋 武昌区期末)如图甲所示,物块A和B叠放在水平地面上。敲击B,B立即获得水平向右的初速度v0,A、B都向右运动,A始终没有从B上滑落,最终两物块都运动至停下来。这段过程中,B的v﹣t关系图线如图乙所示,已知A与B、B与地面间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.物块A和B的质量相等
B.A与B左端的距离至少为
C.摩擦力对A、B的总冲量大小之比为1:3
D.A和B间因摩擦产生的热量与B和地面间产生热量之比是1:3
(多选)11.(2024秋 开福区校级期末)如图所示,在光滑的水平杆上套有一个质量为m的滑环。滑环上通过一根不可伸缩的轻绳悬挂着一个质量为M的物块(可视为质点),绳长为L。将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆;若滑环不固定时,仍给物块以同样的水平冲量,则(g为重力加速度)( )
A.给物块的水平冲量为2M
B.物块上升的最大高度为
C.物块上升最高时的速度为
D.物块在最低点时对细绳的拉力3Mg
(多选)12.(2024秋 南开区校级期末)一弹射机构的简化模型如图所示,一理想轻质弹簧左端固定在墙上,处于原长时右端到达水平面上的O点。一滑块将弹簧右端压缩到P点,滑块与弹簧没有拴接。静止释放后,弹簧把滑块弹开,滑块运动到O点右侧的Q点停下,已知滑块与水平面间的动摩擦因数处处相同。以O点为坐标原点,水平向右为正方向建立x轴。整个过程滑块的加速度a、动量p、动能Ek及滑块与弹簧组成的系统的机械能E随位置坐标x的变化规律,符合实际的是( )
A. B.
C. D.
三.填空题(共4小题)
13.(2024秋 宝山区校级期中)冰壶运动,又称掷冰壶、“冰上溜石”,是冬奥会上以队为单位在冰上进行的一种投掷性竞赛项目,深受观众喜爱。A、B两冰壶在光滑水平冰面上发生对心正碰前后的x﹣t图像如图所示,已知mA=0.2kg,则根据图像可得物体B的质量为 kg,冰壶之间的碰撞属于 (选填“弹性碰撞”、“完全非弹性碰撞”、“一般碰撞”)。
14.(2024秋 思明区校级月考)如图所示,甲、乙两人各站在静止小车的左右两端,车与地面之间无摩擦,当他们同时相向运动时,发现小车向右运动;则在此过程,甲人的动量大小 (选填“大于”、“等于”或“小于”)乙人的动量大小;甲人对小车水平方向冲量大小 (选填“大于”、“等于”或“小于”)乙人对小车水平方向冲量大小。当两人相遇停下后,小车运动情况为 (选填“匀速向右”、“静止”或“匀速向左”)。
15.(2024秋 思明区校级月考)如图甲所示,质量为1kg的物块静止放在水平地面上,现对物块施加水平向右的外力F,F随时间变化的关系如图乙所示。已知物块与水平地面间的动摩擦因数为0.3,接触面间最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2。则0~2s内,物块受到的摩擦力冲量大小为 N s,6s末,物块的速度大小为 m/s。
16.(2023秋 金台区期末)质量是10g的子弹,以300m/s的速度射入质量是240g、静止在光滑水平桌面上的木块。
(1)如果子弹留在木块中,木块运动的速度是 m/s;
(2)如果子弹把木块打穿,子弹穿过后的速度为100m/s,这时木块的速度又是 m/s。(结果保留两位有效数字)
四.解答题(共4小题)
17.(2024秋 苏州期末)如图所示,P为固定挡板,质量为2m的长木板A以水平初速度v0沿光滑水平面向右运动。某时刻质量为m的小物块B轻轻释放到A的右端,第一次达到共同速度后,B与P发生碰撞,一段时间后B与A第二次达到共同速度,之后B与P发生了多次碰撞,B始终未从A上滑落。已知A、B间的动摩擦因数为μ,重力加速度为g,B与P发生碰撞时无机械能损失且碰撞时间极短。求:
(1)A、B第一次的共同速度大小v1;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功W;
(3)A的最小长度L。
18.(2024秋 盐城期末)高空坠物极易对行人造成伤害。《中华人民共和国民法典》第一千二百五十四条规定:禁止从建筑物中抛掷物品。从建筑物中抛掷物品或者从建筑物上坠落的物品造成他人损害的,由侵权人依法承担侵权责任。若一个50g的生鸡蛋从居民楼的7楼阳台坠下,距离地面的高度大约20m,与地面的撞击时间约为0.01s。(g取10m/s2)求:
(1)鸡蛋着地前瞬间的速度大小;
(2)该鸡蛋着地过程中对地面产生的平均冲击力。
19.(2024秋 雨花区校级期末)如图所示,倾角θ=37°的斜面AB与长度为L=0.6m的水平面BC在B点衔接,衔接点平滑,质量为m=1kg的可视为质点的滑块Q静置在水平面的右端C。可视为质点的滑块P自斜面上高h=0.3m处静止释放,与滑块Q发生弹性碰撞后,滑块Q在C点立即进入光滑竖直半圆轨道DE的内侧(CD间隙不计),D为圆的最高点,圆半径记为R。滑块Q经圆弧后在E点水平抛出,最终落于水平地面FG上,水平面FG与BC的高度差为H=1.2m。已知滑块P与AB面和BC面的动摩擦因数都为μ=0.1。
(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①求滑块Q进入D点时的速度vD。
②求半圆轨道的半径R的取值范围。
③求滑块Q离开E后落在FG面上的最大射程。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,求滑块Q进入D点时对D的压力大小的范围。
20.(2024秋 无锡期末)如图所示,小车上固定有处于竖直平面内的特殊形状的光滑圆管,其中AB段圆弧所对应的半径R1=0.5m,圆心角∠AOB=53°,BC段对应的半径R2=0.35m,是四分之一圆弧,B点切线方向竖直,C点与小车表面平滑衔接,小车CD部分与小球之间的动摩擦因数μ=0.4。质量M=2kg的小车(含圆管)静止放置于光滑的水平地面上,现将质量m=2kg的小球由A点左上方某点以v0=4m/s的初速度水平抛出,使小球刚好可以无碰撞的进入到圆管中。小球穿过圆管后,滑上CD段。不计空气阻力,取g=10m/s2,sin53°=0.8,cos53°=0.6,求:
(1)小球从抛出点到A点竖直高度;
(2)小球刚运动到C点时,小车的速度大小;
(3)要使小球不从车上落下,则CD长度至少是多少?
高考物理高频易错押题预测 动量与动量守恒定律
参考答案与试题解析
一.选择题(共8小题)
1.(2025 庐阳区校级模拟)图为丁俊晖正在准备击球,设丁俊晖在某一杆击球过程中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球A的动量pA=5kg m/s,花色球B静止,碰后花色球B的动量变为P'B=4kg m/s,则两球质量mA与mB间的关系可能是( )
A. B. C.mB=2mA D.mB=5mA
【考点】动量守恒与能量守恒共同解决实际问题;用能量守恒定律解决实际问题.
【专题】应用题;信息给予题;定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】C
【分析】由动量守恒定律,结合弹性碰撞与完全非弹性碰撞两种临界条件,分析碰撞的过程后可能的运动的情况即可。
【解答】解:碰撞过程系统动量守恒,以白色球的初速度方向为正方向,由动量守恒定律得:
pA=pA′+pB′
代入数据得:5kg m/s=pA′+4kg m/s
解得:pA′=1kg m/s,方向与白色球的初速度方向相同。
若碰撞后二者的速度相等(设为v共),则有:
mAv共=pA′=1kg m/s,mBv共=pB′=4kg m/s
联立可得:mB=4mA
若碰撞过程系统的机械能不变,根据碰撞过程总动能不增加,则有:
解得
碰后两球同向运动,A的速度不大于B的速度,则
解得mB≤4mA
综上可知
故C正确,ABD错误。
故选:C。
【点评】该题考查动量守恒定律以及碰撞的特点,考虑弹性碰撞与完全非弹性碰撞,即可求出可能的质量关
2.(2024秋 南京期末)如图所示,在离地面高为h处将质量为m的小球以初速度v0水平抛出,重力加速度为g,不计空气阻力。下列说法正确的是( )
A.落地前瞬间,小球的动量大小为
B.从抛出到落地,小球所受重力的冲量大小为
C.从抛出到落地,小球动量的变化量方向竖直向上
D.从抛出到落地,小球动量的变化量大小为
【考点】动量定理的内容和应用;平抛运动速度的计算;用动量的定义式计算物体的动量.
【专题】定量思想;推理法;动量定理应用专题;理解能力.
【答案】D
【分析】根据动能定理求解落地时速度大小,再根据动量的计算公式求解落地时物体动量大小;根据运动学公式求落地时间,根据冲量公式求冲量,根据动量定理求解动量变化量。
【解答】解:A、由动能定理
得
动量为
故A错误;
B、由,重力的冲量大小为
故B错误;
CD、合力的冲量等于动量的变化量,由动量定理有
则小球动量的变化量方向竖直向下,其大小为,故C错误,D正确。
故选:D。
【点评】本题主要是考查动量定理,利用动量定理解答问题时,要注意分析运动过程中物体的受力情况,知道合外力的冲量才等于动量的变化。
3.(2024秋 扬州期末)骑电瓶车必须戴好头盔。在头部受到撞击时,其他条件相同,戴头盔与不戴头盔相比,骑行者头部( )
A.动量变化小 B.动量变化慢
C.受到撞击力大 D.受到撞击力的冲量大
【考点】动量定理的内容和应用.
【专题】定性思想;推理法;动量定理应用专题;理解能力.
【答案】B
【分析】骑行者头部的动量的变化量是一定的,再根据动量定理分析。
【解答】解:根据动量定理 I=FΔt=Δp,可得,由于气囊的缓冲与头部的撞击时间Δt延长了,从而减小了对头部的作用力F,也即减小了驾驶员头部撞击过程中的动量变化快慢,但驾驶员头部撞击过程中动量变化量和撞击力的冲量I并未改变,故B正确,ACD错误。
故选:B。
【点评】本题考查了动量定理在实际生活中的应用,要注意明确头盔增加了冲击时间,从而减小了冲击力。
4.(2024秋 徐州期末)做自由落体运动的物体,其动量p与时间t的p﹣t关系图线为( )
A. B.
C. D.
【考点】动量定理的内容和应用;自由落体运动的规律及应用.
【专题】定性思想;推理法;动量定理应用专题;理解能力.
【答案】B
【分析】明确自由落体的物体只受重力,加速度恒定不变,速度和时间成正比,再由动量的表达式分析即可。
【解答】解:自由落体运动的加速度是恒定不变的,由v=at可知,物体的速度与时间成正比,由p=mv=mat,可知动量与时间成正比,故B正确,ACD错误;
故选:B。
【点评】本题考查图象以及自由落体运动的规律,要注意掌握用图象来描述物体的运动性质的方法。
5.(2024秋 郴州期末)三个完全相同的小球,质量均为m,其中小球A、B固定在竖直轻杆的两端,A球紧贴竖直光滑墙面,B球位于足够大的光滑水平地面上,小球C紧贴小球B,如图所示,三小球均保持静止。某时,小球A受到轻微扰动开始顺着墙面下滑,直至小球A落地前瞬间的运动过程中,三小球始终在同一竖直面上。已知小球C的最大速度为v,轻杆长为L,重力加速度为g,下列关于该过程的说法中正确的是( )
A.A、B、C三球组成的系统动量守恒
B.竖直墙对小球A的冲量大小为3mv
C.小球A落地前瞬间,动能大小为
D.小球A落地前瞬间,小球C的速度是小球B速度的2倍
【考点】动量守恒定律的内容、条件和判断;多物体系统的机械能守恒问题.
【专题】定量思想;推理法;动量与动能定理或能的转化与守恒定律综合;推理论证能力.
【答案】C
【分析】分析小球的运动特点和运动过程中的临界状态;根据动量守恒定律和几何关系得出小球的速度关系,结合能量关系完成分析。
【解答】解:A、A、B、C三球组成的系统在水平方向合外力不为零,受墙的推力,竖直方向合外力也不为零,故动量不守恒,故A错误;
B、B和C分离后小球C做匀速直线运动,所以B、C分离时,两球速度均为v,对三小球整体列水平方向动量定理,则墙对小球A的冲量I=2mv,故B错误;
C、轻杆对小球A做功大小等于对小球B做功大小,即等于小球B、C的动能增量,则,小球A落地前瞬间动能大小为EkA=mgL﹣W,解得,故C正确;
D、自小球A离开墙面到小球落地,A、B组成的系统水平方向动量守恒,规定向右为正方向,则mv=mvB+mvAx且有vB=vAx解得,小球C的速度是小球A水平速度的2倍,但小球A有竖直速度分量,故D错误。
故选:C。
【点评】本题主要考查了动量守恒定律的相关应用,理解动量守恒的条件,结合能量守恒定律和关联速度的特点即可完成分析。
6.(2024秋 徐州期末)为确保公共安全,市民遛狗时应牵绳。如图所示,一市民遛狗时匀速前行,已知绳中拉力大小为F、方向与水平面夹角为θ。则在t时间内拉力的冲量为( )
A.0
B.Ft,方向与F方向一致
C.Ftcosθ,方向与F方向一致
D.Ftcosθ,方向沿水平方向向左
【考点】求恒力的冲量.
【专题】定量思想;控制变量法;动量定理应用专题;理解能力.
【答案】B
【分析】根据冲量公式进行计算。
【解答】解:根据冲量公式可得
I=Ft
方向与F方向相同,故B正确,ACD错误。
故选:B。
【点评】本题考查的是恒力做功,直接利用公式求解,题型简单。
7.(2024秋 扬州期末)如图所示,在水平桌面上,粘在一起的两个一元硬币甲与静止的一元硬币乙发生一维碰撞。在下列描述甲、乙速度v与时间t的关系图像中,可能正确的是( )
A. B.
C. D.
【考点】分析碰撞的合理性.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】A
【分析】根据动量守恒定律结合图像斜率的意义分析。
【解答】解:硬币与桌面的动摩擦因数相同,根据μmg=ma
可知a=μg
则图像的斜率应相同;
规定向右为正方向,根据动量守恒定律有2mv0=2mv1+mv2
图像中每个单位格设为1,代入验证可知A符合,故A正确,BCD错误;
故选:A。
【点评】本题考查动量守恒定律,解题关键掌握图像的认识,注意动量守恒的条件。
8.(2024秋 南京期末)如图所示,在光滑的水平桌面上有体积相同的两个小球A、B,质量分别为m=0.1kg和M=0.3kg,两球中间夹着一根压缩的轻弹簧,原来处于静止状态,同时放开A、B球和弹簧,已知A球脱离弹簧的速度为6m/s,接着A球进入与水平面相切,半径为0.5m的竖直面内的光滑半圆形轨道运动,PQ为半圆形轨道竖直的直径,g=10m/s2,下列说法正确的是( )
A.弹簧弹开过程,弹力对A的冲量与弹力对B的冲量相同
B.刚开始弹簧的弹性势能大小为2.0J
C.A球从P点运动到Q点过程中所受合外力的冲量大小为0.2N s
D.若使A球不能到达Q点,则半圆轨道半径的最小值为0.72m
【考点】动量守恒与能量守恒共同解决实际问题;绳球类模型及其临界条件;动能定理的简单应用;动量定理的内容和应用.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】D
【分析】根据弹簧对A、B的弹力关系、作用时间关系分析弹力对A、B冲量大小关系;弹簧弹开过程,根据动量守恒定律求A球脱离弹簧时A、B球获得的速度,根据能量守恒定律计算最大弹性势能;由机械能守恒定律求A球到达Q点的速度,再由动量定理求A球从P点运动到Q点过程中所受合外力的冲量大小;在最高点根据牛顿第二定律结合机械能守恒定律解答。
【解答】解:A.弹簧弹开过程,弹簧对A、B的弹力大小相等、方向相反、作用时间相等,由I=Ft可知,弹力对A、B的冲量大小相等,方向相反,故A错误;
B.释放弹簧过程中,A、B系统动量守恒,设A球脱离弹簧时A、B的速度大小分别为v1、v2,以向右为正方向,由动量守恒定律得:mv1﹣Mv2=0
由题知:v1=6m/s
解得:v2=2m/s
根据机械能守恒定律可得,刚开始弹簧的弹性势能大小为:
解得:Ep=2.4J,故B错误;
C.设A球至Q点的速度大小为vQ,A球从P点运动到Q点过程中只有重力做功,机械能守恒,取水平桌面为零势能面,由机械能守恒定律得:mg 2R
解得:vQ=4m/s
小球A从P点运动到Q点过程中,取水平向左为正方向,
由动量定理可知,A球从P点运动到Q点过程中所受合外力的冲量大小为:IA=mvQ﹣m(﹣v1)=m(vQ+v1)=0.1×(4+6)N s=1N s,故C错误;
D.A球恰能到达最高点时有mg
A球从最低点到最高点有﹣mg×2R
解得R=0.72m
则若使A球不能到达Q点,则半圆轨道半径的最小值为0.72m,故D正确;
故选:D。
【点评】本题主要是考查了动量守恒定律和机械能守恒定律;对于动量守恒定律,其守恒条件是:系统不受外力作用或合外力为零;解答时要首先确定一个正方向,利用碰撞前系统的动量和碰撞后系统的动量相等列方程求解。
二.多选题(共4小题)
(多选)9.(2024秋 长沙期末)如图甲所示,倾角为30°的光滑斜面(足够长)固定在水平面上,质量为2kg的物块静止在斜面底端,t=0时刻给物块施加沿斜面方向的作用力F,物块运动的a﹣t图像如图乙所示,取沿斜面向上为正方向,重力加速度g=10m/s2,下列说法中正确的有( )
A.前2s内F的大小是第3s的2倍
B.3s内物块所受合力的冲量为零
C.3s内力F做功为零
D.3s内力F的冲量为30N s
【考点】动量定理的内容和应用;重力做功的特点和计算;动能定理的简单应用.
【专题】定量思想;推理法;动量定理应用专题;推理论证能力.
【答案】ABD
【分析】根据牛顿第二定律求解外力,再根据运动学公式求解位移,再求出拉力做的功;根据冲量的计算公式求解冲量。
【解答】解:A、0~2s内,根据牛顿第二定律得:F1﹣mgsin30°=ma1,得:F1=20N
在2~3s内,根据牛顿第二定律得:F2+mgsin 30°=ma2,得:F2=10N
则前2s内F的大小是第3s的2倍,故A正确;
B、图像与坐标轴围成的面积代表合力的冲量;3s内物块所受合力的冲量为I=(5×2﹣10×1)N s=0,故B正确;
C、0~2s内,物体的位移为x1m=10m,2~3s内,物体的位移为x2m=5m
所以3s内力F做功为W=F1x1﹣F2x2=20×10J+10×5J=150J,故C错误;
D、设F1的方向为正方向,根据冲量的计算公式可知3s内力F的冲量为IF=F1t1﹣F2t2=20×2N s﹣10×1N s=30N s,故D正确;
故选:ABD。
【点评】本题主要是考查牛顿运动定律的综合应用、功的计算以及冲量的计算等,能够根据图象分析受力情况,再结合运动学公式、功的计算公式求解是关键。
(多选)10.(2024秋 武昌区期末)如图甲所示,物块A和B叠放在水平地面上。敲击B,B立即获得水平向右的初速度v0,A、B都向右运动,A始终没有从B上滑落,最终两物块都运动至停下来。这段过程中,B的v﹣t关系图线如图乙所示,已知A与B、B与地面间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.物块A和B的质量相等
B.A与B左端的距离至少为
C.摩擦力对A、B的总冲量大小之比为1:3
D.A和B间因摩擦产生的热量与B和地面间产生热量之比是1:3
【考点】动量定理的内容和应用;有外力的水平板块模型;常见力做功与相应的能量转化;求变力的冲量.
【专题】定量思想;推理法;动量定理应用专题;功能关系 能量守恒定律;推理论证能力.
【答案】AD
【分析】根据图像得到A、B的加速度,然后根据牛顿第二定律得到它们的质量关系;根据动量定理得到它们的动量变化关系;根据平均速度得到它们的位移,然后可得它们的相对位移;根据摩擦力与相对位移的乘积分别得到A和B、B和地面之间因摩擦产生的热量。
【解答】解:A、设A的质量为mA,B的质量为mB,动摩擦因数大小为μ,根据图像可知B的加速度大小为aB,,对A根据牛顿第二定律有μmAg=mAaA,对B根据牛顿第二定律有μmAg+μ(mA+mB)g=mBaB,联立解得mA=mB,故A正确;
C、A的初速度为零,最后和B静止在地面上,根据动量定理可知摩擦力对A的冲量大小为0,摩擦力对B的冲量大小为mBv0,故C错误;
B、开始时A加速,B减速运动,当A、B速度相等后一起减速运动,所以A与B左端的距离至少为,解得,故B错误;
D、A和B间因摩擦产生的热量为Q=μmAgΔx,B与地面之间因摩擦产生的热量为Q',整理得Q',则Q:Q'=1:3,故D正确。
故选:AD。
【点评】本题考查了动量定理、牛顿第二定律和功能关系相关内容,综合性较强。
(多选)11.(2024秋 开福区校级期末)如图所示,在光滑的水平杆上套有一个质量为m的滑环。滑环上通过一根不可伸缩的轻绳悬挂着一个质量为M的物块(可视为质点),绳长为L。将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆;若滑环不固定时,仍给物块以同样的水平冲量,则(g为重力加速度)( )
A.给物块的水平冲量为2M
B.物块上升的最大高度为
C.物块上升最高时的速度为
D.物块在最低点时对细绳的拉力3Mg
【考点】动量守恒与能量守恒共同解决实际问题;牛顿第二定律与向心力结合解决问题;机械能守恒定律的简单应用;动量定理的内容和应用;某一方向上的动量守恒问题.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】BD
【分析】A.将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆,根据机械能守恒定律、冲量的计算公式分别列式,即可分析判断;
BC.滑环不固定时,物块和滑环组成的系统机械能守恒,水平方向动量守恒,据此列式,即可分析判断;
D.结合前面分析,由牛顿第二定律列式,即可分析判断。
【解答】解:A.设物块初速度大小为v0,
将滑环固定时,极短时间内给物块一个水平冲量,物块摆起后刚好碰到水平杆,根据机械能守恒定律可得:,
解得:,
故给物块的水平冲量大小为:,故A错误;
BC.滑环不固定时,物块初速度大小仍为v0,设物块摆至最大高度h时,滑块与物块速度大小都为v,
在此过程中物块和滑环组成的系统机械能守恒,水平方向动量守恒,以物块初速度的方向为正方向,
由该系统水平方向动量守恒可得:Mv0=(m+M)v,
由该系统机械能守恒可得:,
联立可得:,,故B正确,C错误;
D.对m、M组成的系统,当M第一次回到最低点时,由该系统水平方向动量守恒和能量守恒可知,m、M的相对速度大小仍然为v0,
则在最低点,由牛顿第二定律可知:T,
解得:T=3Mg,故D正确;
故选:BD。
【点评】本题主要考查动量守恒与能量守恒共同解决实际问题,解题时需注意挖掘临界条件:在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,即速度相等或位移相等时。
(多选)12.(2024秋 南开区校级期末)一弹射机构的简化模型如图所示,一理想轻质弹簧左端固定在墙上,处于原长时右端到达水平面上的O点。一滑块将弹簧右端压缩到P点,滑块与弹簧没有拴接。静止释放后,弹簧把滑块弹开,滑块运动到O点右侧的Q点停下,已知滑块与水平面间的动摩擦因数处处相同。以O点为坐标原点,水平向右为正方向建立x轴。整个过程滑块的加速度a、动量p、动能Ek及滑块与弹簧组成的系统的机械能E随位置坐标x的变化规律,符合实际的是( )
A. B.
C. D.
【考点】动量定理的内容和应用;动能定理的简单应用;常见力做功与相应的能量转化.
【专题】定性思想;推理法;动量和能量的综合;推理论证能力.
【答案】AC
【分析】根据各个物理量的表达式得到对应物理量与x的函数关系式,根据函数关系式判断图像是否正确。
【解答】解:A.当滑块在O点左侧位置坐标为x时,弹簧压缩量为x,设滑块的质量为m,弹簧的劲度系数为k,滑块与水平面间的动摩擦因数为μ,由牛顿第二定律,有﹣kx﹣μmg=ma
得
当滑块在O点右侧时,有﹣μmg=ma
得a=﹣μga﹣x图像为两段直线,故A正确。
B.取一段位移微元Δx,可认为滑块的加速度不变,设为a,速度为v,有
设滑块运动到N处时弹簧弹力等于摩擦力,加速度为0,由P到N,加速度逐渐减小,速度逐渐增大,逐渐减小,p﹣x图线的斜率逐渐减小;到N处时p﹣x图线的斜率减为0;由N到O,加速度反向逐渐增大,速度逐渐减小,绝对值逐渐增大,p﹣x图线的斜率绝对值逐渐增大;由O到Q,加速度不变,速度逐渐减小,绝对值逐渐增大,p﹣x图线的斜率绝对值逐渐增大,p﹣x图像O点右侧不可能为倾斜的直线,故B错误。
C.滑块移动位移微元Δx,由动能定理有
F合Δx=ΔEk
可得
,Ek﹣x图像由P到N斜率减小,由N到O斜率绝对值增大,O点右侧斜率不变,为倾斜的直线,故C正确。
D.由能量转化可知,滑块克服摩擦力做的功等于系统机械能的减少量。对一段位移微元Δx,有﹣μmgΔx=ΔE
可知
即E﹣x图像为斜率不变的倾斜的直线,故D错误。
故选:AC。
【点评】通过斜率变化判断图像是否正确是本题解题关键。
三.填空题(共4小题)
13.(2024秋 宝山区校级期中)冰壶运动,又称掷冰壶、“冰上溜石”,是冬奥会上以队为单位在冰上进行的一种投掷性竞赛项目,深受观众喜爱。A、B两冰壶在光滑水平冰面上发生对心正碰前后的x﹣t图像如图所示,已知mA=0.2kg,则根据图像可得物体B的质量为 0.6 kg,冰壶之间的碰撞属于 弹性碰撞 (选填“弹性碰撞”、“完全非弹性碰撞”、“一般碰撞”)。
【考点】用动量守恒定律解决简单的碰撞问题;利用x﹣t图像的斜率求解物体运动的速度.
【专题】定量思想;推理法;动量与动能定理或能的转化与守恒定律综合;分析综合能力.
【答案】0.6,弹性碰撞。
【分析】根据x﹣t图线斜率求速度,根据动量守恒定律求质量,然后计算碰撞前后的机械能总量关系,即可解答。
【解答】解:x﹣t图线的斜率表示速度,则碰撞前,有,vB=0
碰撞后,m/s=﹣2m/s,m/s=2m/s
以碰撞前A的方向为正方向,由动量守恒定律可知
mAvA+mBvB=mAvA′+mBvB′
代入数据解得mB=0.6kg
碰撞前总动能为1.6J
碰撞后总动能为EK′mAvA′2mBvB′2
代入数据解得EK′=1.6J
碰撞前后重力势能不变,则碰撞前后机械能守恒,两冰壶发生的是弹性碰撞。
故答案为:0.6,弹性碰撞。
【点评】本题是一道综合题,需要学生根据x﹣t图线求速度,再判断机械能,难度中等。
14.(2024秋 思明区校级月考)如图所示,甲、乙两人各站在静止小车的左右两端,车与地面之间无摩擦,当他们同时相向运动时,发现小车向右运动;则在此过程,甲人的动量大小 小于 (选填“大于”、“等于”或“小于”)乙人的动量大小;甲人对小车水平方向冲量大小 小于 (选填“大于”、“等于”或“小于”)乙人对小车水平方向冲量大小。当两人相遇停下后,小车运动情况为 静止 (选填“匀速向右”、“静止”或“匀速向左”)。
【考点】动量守恒定律的一般应用.
【专题】应用题;定量思想;推理法;动量和能量的综合;分析综合能力.
【答案】小于;小于;静止。
【分析】甲、乙两人相向而行的过程中,甲、乙两人及小车组成的系统在水平方向所受的合外力为零,系统动量守恒,根据动量守恒定律列式分析即可。
【解答】解:甲、乙两人相向而行的过程中,甲、乙两人及小车组成的系统在水平方向所受的合外力为零,系统动量守恒,
以向右为正方向,在水平方向,根据动量守恒定律得:m甲v甲+m乙v乙+m车v车=0
小车向右运动,小车的动量方向向右,说明甲与乙两人的总动量向左,因乙向左运动,甲向右运动,则甲的动量必定小于乙的动量;
小车向右运动,对小车,由动量定理可知,小车受外力的冲量向右,人在行走时对小车的作用力冲量与人的运动方向相反,则说明乙对小车的作用力冲量大于甲对小车的作用力冲量;
两人与车组成的系统动量守恒,系统初状态动量为零,当两人都停下后两人的动量都为零,由动量守恒定律可知,小车的动量也为零,小车静止。
故答案为:小于;小于;静止。
【点评】本题考查动量守恒定律和动量定理的直接应用,关键要掌握动量守恒的条件:合外力为零,要注意速度和动量的矢量性。
15.(2024秋 思明区校级月考)如图甲所示,质量为1kg的物块静止放在水平地面上,现对物块施加水平向右的外力F,F随时间变化的关系如图乙所示。已知物块与水平地面间的动摩擦因数为0.3,接触面间最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2。则0~2s内,物块受到的摩擦力冲量大小为 4.5 N s,6s末,物块的速度大小为 13.5 m/s。
【考点】F﹣t图像中的动量问题;求恒力的冲量;用动量定理求平均作用力.
【专题】定量思想;推理法;动量定理应用专题;推理论证能力.
【答案】4.5;13.5。
【分析】根据题意求最大静摩擦力,再结合图像分析运动情况,由冲量的概念、动量定理等列式代入数据计算。
【解答】解:物块与水平地面间的最大静摩擦力为fmax=μmg=0.3×1×10N=3N
由F﹣t图像可知,在0~1s内物块受到静摩擦力作用,则0~2s内,物块受到的摩擦力冲量大小为
在t=1s时物块开始运动,则1~6s内,对物块根据动量定理可得I合=IF﹣If=mv﹣0
其中;If=3×5N s=15N s
代入数据解得6s末物块的速度大小v=13.5m/s。
故答案为:4.5;13.5。
【点评】本题主要考查F﹣t图像中的动量问题,解题时需注意,F﹣t图像与坐标轴所围面积,表示该力冲量。
16.(2023秋 金台区期末)质量是10g的子弹,以300m/s的速度射入质量是240g、静止在光滑水平桌面上的木块。
(1)如果子弹留在木块中,木块运动的速度是 12 m/s;
(2)如果子弹把木块打穿,子弹穿过后的速度为100m/s,这时木块的速度又是 8.3 m/s。(结果保留两位有效数字)
【考点】动量守恒定律在子弹打物块模型中的应用.
【专题】定量思想;寻找守恒量法;动量定理应用专题;分析综合能力.
【答案】(1)12;(2)8.3。
【分析】(1)(2)子弹射入木块的过程和打穿木块的过程,分别根据动量守恒定律求解木块运动的速度。
【解答】解:(1)取子弹的初速度方向为正方向,根据动量守恒定律有
m1v0=(m1+m2)v共
解得
v共=12m/s
则子弹留在木块中,木块运动的速度是12m/s;
(2)取子弹的初速度方向为正方向,根据动量守恒定律有
m1v0=m1v1+m2v2
解得木块的速度为
v2≈8.3m/s
故答案为:(1)12;(2)8.3。
【点评】对于子弹打木块的过程,要掌握其基本规律是动量守恒定律,要明确规定正方向,用正负号表示速度方向。
四.解答题(共4小题)
17.(2024秋 苏州期末)如图所示,P为固定挡板,质量为2m的长木板A以水平初速度v0沿光滑水平面向右运动。某时刻质量为m的小物块B轻轻释放到A的右端,第一次达到共同速度后,B与P发生碰撞,一段时间后B与A第二次达到共同速度,之后B与P发生了多次碰撞,B始终未从A上滑落。已知A、B间的动摩擦因数为μ,重力加速度为g,B与P发生碰撞时无机械能损失且碰撞时间极短。求:
(1)A、B第一次的共同速度大小v1;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功W;
(3)A的最小长度L。
【考点】动量守恒定律在板块模型中的应用;常见力做功与相应的能量转化.
【专题】定量思想;推理法;动量与动能定理或能的转化与守恒定律综合;推理论证能力.
【答案】(1)A、B第一次的共同速度大小为v0;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功为;
(3)A的最小长度为。
【分析】(1)根据动量守恒定律分析解答;
(2)根据动量守恒定律结合动能定理分析解答;
(3)整个过程中,B相对于A一直向左运动,最终两者速度都为零,根据能量守恒定律解答。
【解答】解:(1)从B滑上A到第一次达到共同速度v1,规定向右为正方向,根据系统动量守恒有
2mv0=(m+2m)v1
得v1v0
(2)从第一次碰撞后到第二次达到共同速度v2,取向右为正方向,根据系统动量守恒有
2mv1﹣mv1=3mv2
得v2v1v0
从开始到第二次达到共同速度过程中,对A运用动能定理
W22
得B对A做的功W
(3)整个过程中,B相对于A一直向左运动,最终两者速度都为零
设两者相对运动的距离为x,A、B系统能量守恒
2μmgx
得x
则为使整个运动过程中B不从A上滑落,A的最小长度L=x
答:(1)A、B第一次的共同速度大小为v0;
(2)A、B从开始到第二次达到共同速度过程中,B对A做的功为;
(3)A的最小长度为。
【点评】本题主要是考查动量守恒定律和能量守恒定律;解答时要首先确定一个正方向,利用碰撞前系统的动量和碰撞后系统的动量相等列方程,再根据能量关系列方程求解。
18.(2024秋 盐城期末)高空坠物极易对行人造成伤害。《中华人民共和国民法典》第一千二百五十四条规定:禁止从建筑物中抛掷物品。从建筑物中抛掷物品或者从建筑物上坠落的物品造成他人损害的,由侵权人依法承担侵权责任。若一个50g的生鸡蛋从居民楼的7楼阳台坠下,距离地面的高度大约20m,与地面的撞击时间约为0.01s。(g取10m/s2)求:
(1)鸡蛋着地前瞬间的速度大小;
(2)该鸡蛋着地过程中对地面产生的平均冲击力。
【考点】动量定理的内容和应用;自由落体运动的规律及应用;牛顿第三定律的理解与应用.
【专题】定量思想;推理法;动量定理应用专题;理解能力.
【答案】(1)鸡蛋着地前瞬间的速度大小为20m/s;
(2)该鸡蛋着地过程中对地面产生的平均冲击力为100.5N。
【分析】(1)根据鸡蛋下落的总高度,计算鸡蛋落地时速度大小;
(2)再根据动量定理列方程求解地面对鸡蛋的冲击力,从而得到鸡蛋对地面产生的冲击力。
【解答】解:(1)鸡蛋下落过程有
v2=2gh
可得鸡蛋落地时速度为
v=20m/s
(2)鸡蛋与地面的撞击过程,取竖直向下为正方向,根据动量定理有
(mg﹣F)t=0﹣mν
代入数据得
F=100.5N
根据牛顿第三定律可知,该鸡蛋对地面产生的冲击力约为100.5N。
答:(1)鸡蛋着地前瞬间的速度大小为20m/s;
(2)该鸡蛋着地过程中对地面产生的平均冲击力为100.5N。
【点评】本题主要考查动量定理,利用动量定理解答问题时,要注意灵活选择研究过程,分析运动过程中物体的受力情况,规定正方向,用正负号表示矢量的方向。
19.(2024秋 雨花区校级期末)如图所示,倾角θ=37°的斜面AB与长度为L=0.6m的水平面BC在B点衔接,衔接点平滑,质量为m=1kg的可视为质点的滑块Q静置在水平面的右端C。可视为质点的滑块P自斜面上高h=0.3m处静止释放,与滑块Q发生弹性碰撞后,滑块Q在C点立即进入光滑竖直半圆轨道DE的内侧(CD间隙不计),D为圆的最高点,圆半径记为R。滑块Q经圆弧后在E点水平抛出,最终落于水平地面FG上,水平面FG与BC的高度差为H=1.2m。已知滑块P与AB面和BC面的动摩擦因数都为μ=0.1。
(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①求滑块Q进入D点时的速度vD。
②求半圆轨道的半径R的取值范围。
③求滑块Q离开E后落在FG面上的最大射程。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,求滑块Q进入D点时对D的压力大小的范围。
【考点】动量守恒与能量守恒共同解决实际问题;平抛运动速度的计算;绳球类模型及其临界条件;动能定理的简单应用.
【专题】定量思想;推理法;动量和能量的综合;推理论证能力.
【答案】(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①滑块Q进入D点时的速度vD大小为2m/s,方向水平向右;
②半圆轨道的半径R的取值范围为:0.2m≤R≤0.4m;
③滑块Q离开E后落在FG面上的最大射程为1.4m。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,滑块Q进入D点时对D的压力大小的范围为:0≤FN<30N。
【分析】(1)①滑块P从静止到C点,根据动能定理列式,滑块P与滑块Q碰撞时动量守恒、且碰撞过程无动能损失,据此列式,即可联立求解;
②在D点能够做圆周运动,根据牛顿第二定律可列式,D点到E点的过程,根据能量守恒定律列式,在E点,根据牛顿第二定律列式,即可联立求解;
③滑块自E点作平抛运动,则水平方向做匀速直线运动、竖直方向做自由落体运动,根据运动学规律列式,结合②及数学知识,即可分析求解。
(2)同(1)思路,由动能定理、弹性碰撞的性质、牛顿第二定律分别列式,即可分析求解。
【解答】解:(1)①滑块P从静止到C点,根据动能定理可得:
,
解得:
vC=2m/s,
滑块P与滑块Q碰撞时动量守恒,以水平向右为正方向,则有:
mvC=mvC'+mvD,
又因为是弹性碰撞,则碰撞过程无动能损失,有:
,
联立可得:
vD=2m/s,方向水平向右;
②在D点能够做圆周运动,根据牛顿第二定律可知:
,
解得:
R≤0.4m,
D点到E点的过程,根据能量守恒定律有:
,
在E点,根据牛顿第二定律有:
,
且:
FN≤70N,
联立得:
R≥0.2m,
所以R的取值范围为:
0.2m≤R≤0.4m;
③滑块自E点作平抛运动,水平方向做匀速直线运动,则射程为:
x=vEt,
竖直方向做自由落体运动,有:
,
结合②,联立可得:
,
有数学知识可得,当R=0.25m时,射程最大,
解得:xmax=1.4m;
(2)由动能定理有:
,
解得:
vC=2m/s,
滑块P与滑块Q碰撞时动量守恒,以水平向右为正方向,则有:
m1vC=m1v1+mv2,
又因为是弹性碰撞,则碰撞过程动能无损失,则有:
,
联立可得:
,
即:
,
则:
0<v2<2vC,
由牛顿第二定律可得:
,
解得:
0≤FN<30N;
答:(1)若滑块P的质量为m=1kg,半圆轨道DE的半径R可调,半圆轨道能承受的滑块的压力不能超过70N,要保证滑块Q能经圆周运动顺利经过E点。
①滑块Q进入D点时的速度vD大小为2m/s,方向水平向右;
②半圆轨道的半径R的取值范围为:0.2m≤R≤0.4m;
③滑块Q离开E后落在FG面上的最大射程为1.4m。
(2)若半圆轨道DE的半径为R=0.4m,滑块P的质量可调,滑块Q进入D点时对D的压力大小的范围为:0≤FN<30N。
【点评】本题主要考查动量守恒与能量守恒共同解决实际问题,解题时需注意挖掘临界条件:在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,即速度相等或位移相等时。
20.(2024秋 无锡期末)如图所示,小车上固定有处于竖直平面内的特殊形状的光滑圆管,其中AB段圆弧所对应的半径R1=0.5m,圆心角∠AOB=53°,BC段对应的半径R2=0.35m,是四分之一圆弧,B点切线方向竖直,C点与小车表面平滑衔接,小车CD部分与小球之间的动摩擦因数μ=0.4。质量M=2kg的小车(含圆管)静止放置于光滑的水平地面上,现将质量m=2kg的小球由A点左上方某点以v0=4m/s的初速度水平抛出,使小球刚好可以无碰撞的进入到圆管中。小球穿过圆管后,滑上CD段。不计空气阻力,取g=10m/s2,sin53°=0.8,cos53°=0.6,求:
(1)小球从抛出点到A点竖直高度;
(2)小球刚运动到C点时,小车的速度大小;
(3)要使小球不从车上落下,则CD长度至少是多少?
【考点】动量守恒与能量守恒共同解决实际问题;平抛运动速度的计算;机械能守恒定律的简单应用.
【专题】定量思想;推理法;力学综合性应用专题;推理论证能力.
【答案】(1)小球从抛出点到A点竖直高度为0.45m;
(2)小球刚运动到C点时,小车的速度大小为6m/s;
(3)要使小球不从车上落下,则CD长度至少是4m。
【分析】(1)小球进入到圆管之前做平抛运动,确定到达A点时速度方向与水平方向的夹角,以及在A点竖直分速度与水平分速度满足的关系,根据竖直方向做自由落体运动求解小球从抛出点到A点竖直高度。
(2)小球穿过圆管的过程,小球与小车组成的的系统在水平方向上动量守恒。根据动量守恒定律与机械能守恒定律求解小球刚运动到C点时,小车的速度大小。
(3)要使小球不从车上落下,CD长度最小时,小球与小车速度相同时,小球刚好滑动到D点。根据动量守恒定律与能量守恒定律解答。
【解答】解:(1)小球进入到圆管之前做平抛运动,到达A点时速度方向与水平方向的夹角为37°,在A点竖直分速度vy与水平分速度vx满足:
,其中:vx=v0=4m/s
解得:vy=3m/s
设小球从抛出点到A点竖直高度为h,由竖直方向做自由落体运动可得:
解得:h=0.45m
(2)小球穿过圆管的过程,小球与小车组成的的系统在水平方向上动量守恒。设小球刚运动到C点时小球的速度为v1,小车的速度为v2。以向右为正方向,根据动量守恒定律与机械能守恒定律分别得:
mv0=mv1+Mv2
解得:v1=﹣2m/s,v2=6m/s
(3)要使小球不从车上落下,CD长度最小(设为Lmin)时,小球与小车速度相同时,小球刚好滑动到D点。以向右为正方向,根据动量守恒定律与能量守恒定律分别得:
mv1+Mv2=(m+M)v共
解得:Lmin=4m
答:(1)小球从抛出点到A点竖直高度为0.45m;
(2)小球刚运动到C点时,小车的速度大小为6m/s;
(3)要使小球不从车上落下,则CD长度至少是4m。
【点评】本题考查了动量守恒定律与能量守恒定律的应用,考查了平抛运动的性质。要注意小球穿过圆管的过程,小球与小车组成的的系统只是在水平方向上满足动量守恒定律。掌握从动量与功能的角度处理问题的方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
