【高考押题卷】2025年高考物理高频易错考前冲刺 匀变速直线运动的研究(含解析)
文档属性
| 名称 | 【高考押题卷】2025年高考物理高频易错考前冲刺 匀变速直线运动的研究(含解析) | 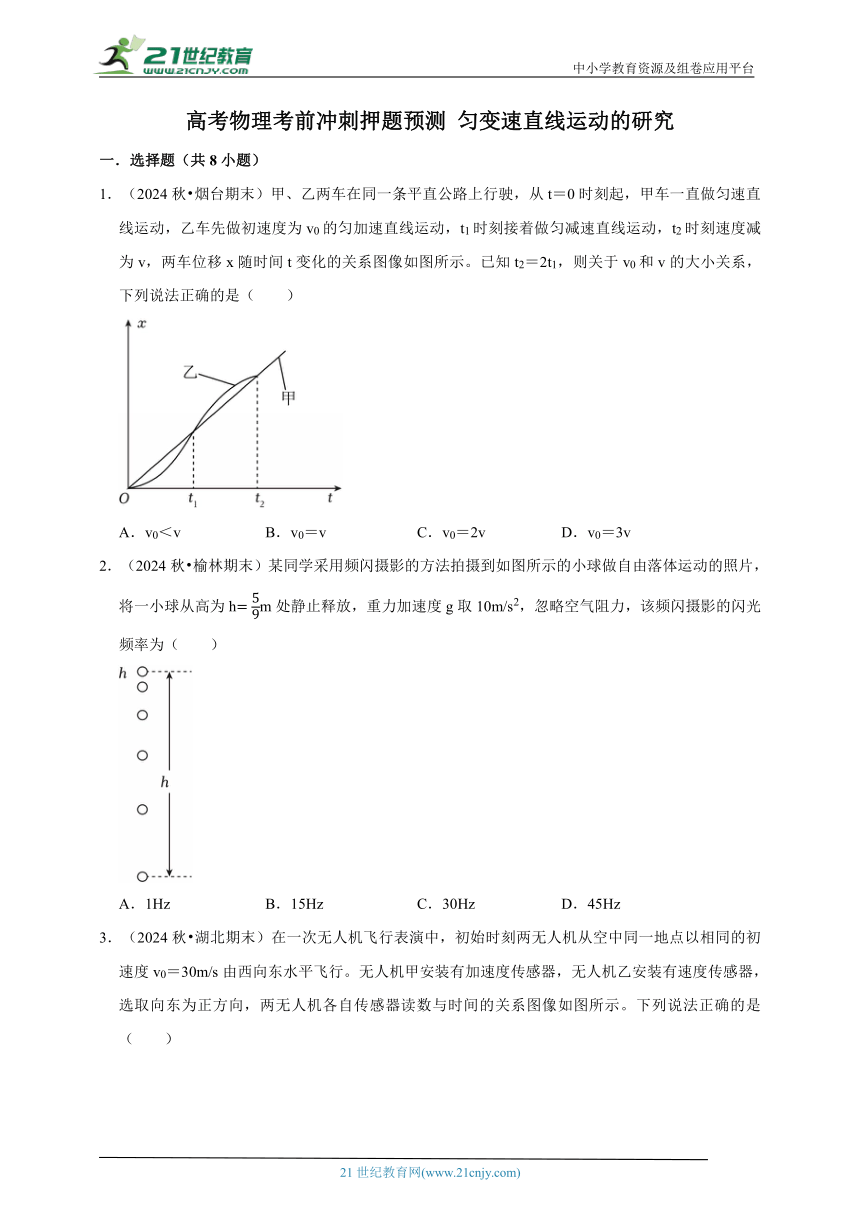 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-28 08:14:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高考物理考前冲刺押题预测 匀变速直线运动的研究
一.选择题(共8小题)
1.(2024秋 烟台期末)甲、乙两车在同一条平直公路上行驶,从t=0时刻起,甲车一直做匀速直线运动,乙车先做初速度为v0的匀加速直线运动,t1时刻接着做匀减速直线运动,t2时刻速度减为v,两车位移x随时间t变化的关系图像如图所示。已知t2=2t1,则关于v0和v的大小关系,下列说法正确的是( )
A.v0<v B.v0=v C.v0=2v D.v0=3v
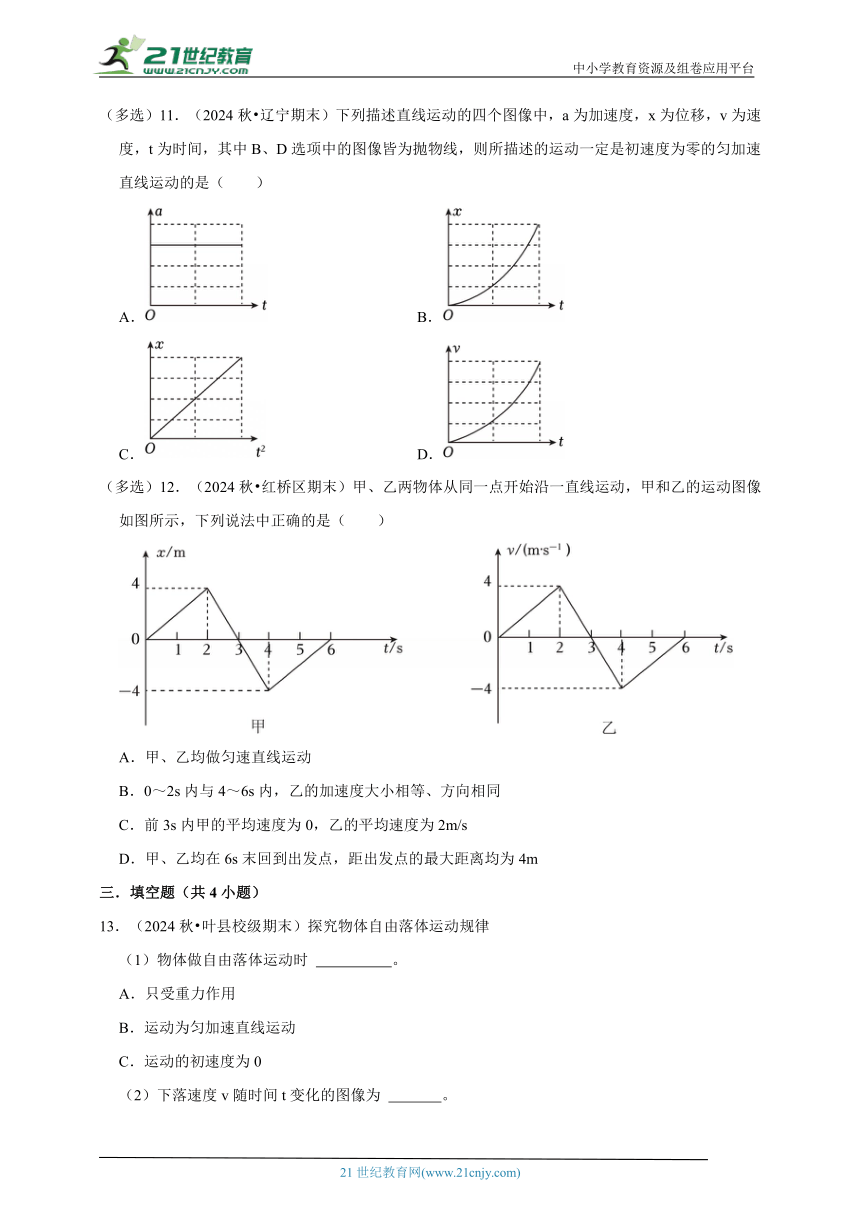
2.(2024秋 榆林期末)某同学采用频闪摄影的方法拍摄到如图所示的小球做自由落体运动的照片,将一小球从高为hm处静止释放,重力加速度g取10m/s2,忽略空气阻力,该频闪摄影的闪光频率为( )
A.1Hz B.15Hz C.30Hz D.45Hz
3.(2024秋 湖北期末)在一次无人机飞行表演中,初始时刻两无人机从空中同一地点以相同的初速度v0=30m/s由西向东水平飞行。无人机甲安装有加速度传感器,无人机乙安装有速度传感器,选取向东为正方向,两无人机各自传感器读数与时间的关系图像如图所示。下列说法正确的是( )
A.3~9s内,甲向东飞行,乙向西飞行
B.3~9s内,甲的加速度与乙的加速度相同
C.9s末甲、乙相距45m
D.0~9s内甲的平均速度为0
4.(2024秋 盐城期末)乙同学为测量自己反应时间,进行了如下实验。如图所示,请甲同学用手捏住直尺,乙用一只手在直尺“0刻度”位置处做捏住直尺准备,在看到甲松手后,乙立刻捏住直尺,读出捏住直尺的刻度,即可算出自己反应时间。后期甲、乙同学又合作设计了一种测量反应时间的“反应时间测量尺”,如图所示,重力加速度g=10m/s2,以下说法正确的是( )
A.甲同学捏住直尺处的刻度值越大,其反应时间越短
B.尺子未竖直对实验结果没有影响
C.直尺刻度20cm处对应“反应时间测量尺”示数0.2s
D.直尺刻度40cm处对应“反应时间测量尺”示数0.4s
5.(2024秋 盐城期末)已知某物体做直线运动,其v﹣t图像如图所示,以下说法正确的是( )
A.前8s内位移为0
B.前8s内位移为12m
C.前4s的位移为12m
D.0~4s内加速度方向与4s~8s内加速度方向相反
6.(2024秋 石景山区期末)某物体位置随时间的关系为x=1+2t+3t2,则关于其速度与1s内的位移大小,下列说法正确的是( )
A.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为6m
B.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为6m
C.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为5m
D.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为5m
7.(2024秋 哈尔滨校级期末)如图甲所示是某无人机的飞行表演,图乙为该无人机表演过程中在竖直方向运动的v﹣t图像,以向上为正方向,下列说法正确的是( )
A.无人机在2s末上升到最高点
B.无人机在3s时加速度为0
C.无人机在1s末和5s末的加速度方向相反
D.无人机在0s﹣2s和2s﹣3s两个阶段的平均速度相等
8.(2024秋 渝中区校级期末)轨道摄影常用于田径比赛,即在最内侧跑道旁铺设固定的轨道,轨道上安装可沿轨道自由移动的高速摄像机,实现跟踪拍摄。在某次百米比赛中,摄像机和运动员的x﹣t图像如图所示,摄像机和运动员均可视为质点,下列说法中正确的是( )
A.摄像机做匀加速直线运动
B.t0时刻摄像机与运动员速度相同
C.0~t0时间内摄像机的平均速度大于运动员的平均速度
D.0~t0时间内摄像机与运动员的距离先变大后变小
二.多选题(共4小题)
(多选)9.(2024秋 海口期末)如图所示,x﹣t图像中两条图线分别表示甲、乙两辆车由同一地点向同一方向运动的情况,下列说法正确的是( )
A.0~6s内,甲车的速度始终小于乙车的速度
B.0~6s内,甲车通过的路程等于乙车通过的路程
C.在6s末,甲、乙两车速度大小相同
D.在6s末,甲、乙两车位于同一位置
(多选)10.(2024秋 水城区期末)0时刻可视为质点的汽车甲、乙在平行的相邻平直车道上并排行驶,两车运动的图像(横轴为时间t)如图所示,下列说法正确的是( )
A.当纵轴为位移(x)时,0~t1内汽车甲的平均速度小于汽车乙的平均速度
B.当纵轴为位移(x)时,0~t2内汽车甲的平均速度小于汽车乙的平均速度
C.当纵轴为速度(v)时,t1时刻甲的加速度大于乙的加速度
D.当纵轴为速度(v)时,t2时刻两车相遇
(多选)11.(2024秋 辽宁期末)下列描述直线运动的四个图像中,a为加速度,x为位移,v为速度,t为时间,其中B、D选项中的图像皆为抛物线,则所描述的运动一定是初速度为零的匀加速直线运动的是( )
A. B.
C. D.
(多选)12.(2024秋 红桥区期末)甲、乙两物体从同一点开始沿一直线运动,甲和乙的运动图像如图所示,下列说法中正确的是( )
A.甲、乙均做匀速直线运动
B.0~2s内与4~6s内,乙的加速度大小相等、方向相同
C.前3s内甲的平均速度为0,乙的平均速度为2m/s
D.甲、乙均在6s末回到出发点,距出发点的最大距离均为4m
三.填空题(共4小题)
13.(2024秋 叶县校级期末)探究物体自由落体运动规律
(1)物体做自由落体运动时 。
A.只受重力作用
B.运动为匀加速直线运动
C.运动的初速度为0
(2)下落速度v随时间t变化的图像为 。
(3)已知在月球表面,重力加速度为地球的。一小球在地球上离地面20m处静止释放,到达地球表面用时 s,在月球上离地面30m处静止释放,到达月球表面用时 s。若一小球在地球表面某一高度静止释放,用时t1,同一高度在月球表面用时t2,则 。(g=10m/s2)
14.(2024秋 闵行区期末)在高度180m处有两只气球(气球a和气球b),以相同速度10m/s分别匀速上升和匀速下降,此时,在这两只气球上各掉出一物体,则这两个物体落到地面时的时间差 s,所经过的路程差 m。(物体空气阻力不计)
15.(2023秋 龙岩期末)高空坠物现象被称为“悬在城市上空的痛”,已成为城市中仅次于交通事故的危险行为。试想一个花盆从高为20m的七楼窗台上坠落,忽略空气阻力,取g=10m/s2。花盆在空中下落的时间为 s;花盆落地时的速度为 m/s;花盆在最后1s内下落的距离为 m。
16.(2023秋 嘉兴期末)汽车A以vA=8m/s的速度做匀速直线运动,发现前方相距x0=14m处、以vB=20m/s的速度同向运动的汽车B正开始匀减速刹车,其刹车的加速度大小a=4m/s2。若汽车B速度减为零后保持静止,则从此刻开始计时,A追上B前,经过时间 s,A、B间的距离最远;经过时间 s,A恰好追上B。
四.解答题(共4小题)
17.(2024秋 水城区期末)2024年8月18日,中国自主设计、自主集成的首台7000米级大深度载人潜水器“蛟龙号”完成了其第300次下潜。在一次模拟下潜中,潜水器(视为质点)由静止开始从海面上竖直向下做匀加速直线运动,下潜x1=160m时潜水器的速度大小v=8m/s,此后潜水器保持该速度匀速运动了t2=100s,最后做匀减速直线运动,下潜一段距离后速度恰好减为零,此时潜水器到水面的距离d=1040m。已知潜水器始终在同一竖直线上运动,求:
(1)潜水器做匀加速运动的加速度大小a1;
(2)潜水器做匀减速运动的加速度大小a2;
(3)潜水器这次下潜的总时间t。
18.(2024秋 水城区期末)如图所示,一辆货车在长坡路段下坡,刹车突然失灵,司机立即关闭发动机,货车以v0=30m/s的速度进入倾角θ=30°的斜面避险车道,滑行一段距离后停下。货车在斜面避险车道滑行的过程中受到空气和斜面的阻力,阻力大小恒为重力大小的,取重力加速度大小g=10m/s2,货车可视为质点。求:
(1)货车减速的加速度大小a;
(2)货车在斜面避险车道上滑行的时间t;
(3)货车在斜面避险车道上滑行的距离x。
19.(2024秋 杭州期末)新能源汽车的智驾系统能够自主决策紧急制动。某新能源汽车在初速为108km/h紧急制动测试中,制动距离为x=45m。如图所示该车又进行自主决策紧急制动测试,待测车以v1=36km/h沿直线CO匀速行驶,车上智驾系统突然探测到“儿童”以v2=1.5m/s恒定速度从前方停靠车辆车头A处窜出沿直线AB运动,智驾系统感知分析后实施紧急制动。已知LAO=3.0m,LBO=1.5m,LCO=16m,汽车制动过程视为匀减速直线运动,“儿童”视为质点。
(1)求紧急制动过程中的加速度大小;
(2)已知该车智驾系统反应时间(从探测到“儿童”到实施紧急制动)Δt=0.2s,求该车停下时车头离O的距离;
(3)过早或频繁紧急制动不利于行车安全和驾乘舒适,若系统经过Δt=0.2s,未实施紧急制动,而是控制汽车在“儿童”到达路边B处时,车头恰好到达O点,则此次制动过程加速度为多大?
20.(2024秋 济宁期末)机器人某次在平台上运送货物时,从A处由静止出发沿两段互相垂直的直线路径AB、BC运动到C处停下。已知机器人最大运行速率vm=3m/s,加速或减速运动时的加速度大小均为a=2m/s2,A到B的时间tAB=3.5s,BC距离xBC=4.5m,机器人途经B处时的速率为零,忽略机器人在B处的转向时间。要求机器人最短时间内到达C处,运动过程中机器人可视为质点。求:
(1)AB间的距离xAB;
(2)机器人从A处运动到C处的平均速度大小(结果保留两位小数)。
高考物理考前冲刺押题预测 匀变速直线运动的研究
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 烟台期末)甲、乙两车在同一条平直公路上行驶,从t=0时刻起,甲车一直做匀速直线运动,乙车先做初速度为v0的匀加速直线运动,t1时刻接着做匀减速直线运动,t2时刻速度减为v,两车位移x随时间t变化的关系图像如图所示。已知t2=2t1,则关于v0和v的大小关系,下列说法正确的是( )
A.v0<v B.v0=v C.v0=2v D.v0=3v
【考点】根据x﹣t图像的物理意义对比多个物体的运动情况.
【专题】定性思想;图析法;运动学中的图象专题;理解能力.
【答案】B
【分析】x﹣t图像的形状反映了物体的位移随时间变化的情况,图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动。
【解答】解:x﹣t图像的斜率表示速度,根据图像可知,乙车两段时间内的平均速度相等,在匀变速直线运动中,平均速度等于初速度和末速度的算术平均值,t1时刻的速度为前段时间的末速度及后段时间的初速度,两者相等,则v0=v,故B正确,ACD错误。
故选:B。
【点评】考查对x﹣t图像的理解,清楚图线的含义。
2.(2024秋 榆林期末)某同学采用频闪摄影的方法拍摄到如图所示的小球做自由落体运动的照片,将一小球从高为hm处静止释放,重力加速度g取10m/s2,忽略空气阻力,该频闪摄影的闪光频率为( )
A.1Hz B.15Hz C.30Hz D.45Hz
【考点】频闪照相法求解自由落体运动.
【专题】定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】B
【分析】根据自由落体运动的位移—时间规律列式求解闪光周期以及频率。
【解答】解:设频闪周期为T,则根据自由落体运动规律有hg(5T)2,代入数据解得Ts,则闪光频率f,解得f=15Hz,故B正确,ACD错误。
故选:B。
【点评】考查自由落体运动的相关规律,会根据题意进行准确分析解答。
3.(2024秋 湖北期末)在一次无人机飞行表演中,初始时刻两无人机从空中同一地点以相同的初速度v0=30m/s由西向东水平飞行。无人机甲安装有加速度传感器,无人机乙安装有速度传感器,选取向东为正方向,两无人机各自传感器读数与时间的关系图像如图所示。下列说法正确的是( )
A.3~9s内,甲向东飞行,乙向西飞行
B.3~9s内,甲的加速度与乙的加速度相同
C.9s末甲、乙相距45m
D.0~9s内甲的平均速度为0
【考点】根据a﹣t图像的物理意义分析物体的运动情况;根据x﹣t图像的物理意义分析单个物体的运动情况.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】C
【分析】由a﹣t图像可以得出甲的加速度变化情况,结合匀变速运动规律求解;v﹣t图像斜率表示加速度,v﹣t图像面积表示位移。
【解答】解:A.3~9s内,乙速度一直为正,向东为正方向,故乙向东飞行,故A错误;
B.v﹣t图像斜率表示加速度,3~9s内,甲的加速度为正,乙的加速度为负,二者方向不同,故B错误;
CD.初速度v0=30m/s,由左图可知,前3s,加速度刚好减为零,位移x1,后面6s,加速运动x2,9s末甲
总位移x甲=x1+x2,解得x甲=135m,0~9s内甲的平均速度一定大于0;v﹣t图像面积表示位移,x乙30m=180m,9s末甲、乙相距180m﹣135m=45m,故C正确,D错误。
故选:C。
【点评】运动类图像问题关键是理解图像的物理意义。
4.(2024秋 盐城期末)乙同学为测量自己反应时间,进行了如下实验。如图所示,请甲同学用手捏住直尺,乙用一只手在直尺“0刻度”位置处做捏住直尺准备,在看到甲松手后,乙立刻捏住直尺,读出捏住直尺的刻度,即可算出自己反应时间。后期甲、乙同学又合作设计了一种测量反应时间的“反应时间测量尺”,如图所示,重力加速度g=10m/s2,以下说法正确的是( )
A.甲同学捏住直尺处的刻度值越大,其反应时间越短
B.尺子未竖直对实验结果没有影响
C.直尺刻度20cm处对应“反应时间测量尺”示数0.2s
D.直尺刻度40cm处对应“反应时间测量尺”示数0.4s
【考点】自由落体运动的规律及应用.
【专题】定量思想;推理法;自由落体运动专题;推理论证能力.
【答案】C
【分析】自由落体时间越长下落的高度越大,由于是匀变速直线运动所以相等的时间下落的高度不同,高度决定时间。
【解答】解:A.乙同学捏住直尺处的刻度值越大,下落的高度越大则反应时间越长,故A错误;
B.如果尺子未竖直,那么直尺下落时速度不能保持一直竖直向下,而且相对来说空气阻力会更大,刻度尺的下落不能近似看成自由落体运动,故B错误;
CD.若乙同学捏住直尺处的刻度值为20cm,根据公式:,则20cm处标注的时间刻度是:,同理40cm处标注的时间刻度是0.2s,不是0.4s,故C正确,D错误。
故选:C。
【点评】本题考查自由落体公式的基本应用,难度适中。
5.(2024秋 盐城期末)已知某物体做直线运动,其v﹣t图像如图所示,以下说法正确的是( )
A.前8s内位移为0
B.前8s内位移为12m
C.前4s的位移为12m
D.0~4s内加速度方向与4s~8s内加速度方向相反
【考点】利用v﹣t图像与坐标轴围成的面积求物体的位移;利用v﹣t图像的斜率求解物体运动的加速度;根据v﹣t图像的物理意义分析单个物体的运动情况.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】A
【分析】v﹣t图像反映了做直线运动的物体的速度随时间变化的规律,斜率表示加速度的大小及方向,图线与时间轴所包围的“面积”表示位移。
【解答】解:AB.v﹣t图线与时间轴所包围的“面积”表示位移,由图可得,前8s内图像在t轴上方和下方的面积相等,前8s内位移为0,故A正确,B错误;
C.v﹣t图线与时间轴所包围的“面积”表示位移,由图可得,前4s的位移为6m,故C错误;
D.v﹣t图像斜率表示加速度的大小及方向,0~4s内加速度方向与4s~8s内加速度方向相同,故D错误。
故选:A。
【点评】考查对v﹣t图像的理解,清楚图线的含义。
6.(2024秋 石景山区期末)某物体位置随时间的关系为x=1+2t+3t2,则关于其速度与1s内的位移大小,下列说法正确的是( )
A.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为6m
B.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为6m
C.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为5m
D.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为5m
【考点】匀变速直线运动位移与时间的关系.
【专题】定量思想;推理法;直线运动规律专题;理解能力.
【答案】C
【分析】根据速度的概念分析速度的物理意义。先确定t=0时刻与t=1s时刻物体的位置,由位置的变化得到位移的大小。
【解答】解:速度是描述物体运动快慢的物理量,运动对应空间位置变化,故速度是描述位置变化快慢的物理量。
物体位置随时间的关系为x=1+2t+3t2(m),则可得t=0时刻,物体位置为x0=1m,t=1s时刻,物体位置为x1=6m
故1s内物体的位移大小为:Δx=x1﹣x0=6m﹣1m=5m,故ABD错误,C正确。
故选:C。
【点评】本题考查学生对速度概念的理解,速度的定义是位移与时间的比值,而位移是物体位置的变化,故速度是刻画物体位置变化快慢的物理量。
7.(2024秋 哈尔滨校级期末)如图甲所示是某无人机的飞行表演,图乙为该无人机表演过程中在竖直方向运动的v﹣t图像,以向上为正方向,下列说法正确的是( )
A.无人机在2s末上升到最高点
B.无人机在3s时加速度为0
C.无人机在1s末和5s末的加速度方向相反
D.无人机在0s﹣2s和2s﹣3s两个阶段的平均速度相等
【考点】利用v﹣t图像的斜率求解物体运动的加速度;利用v﹣t图像与坐标轴围成的面积求物体的位移.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】D
【分析】v﹣t图像的斜率表示加速度,斜率大小表示加速度大小,斜率正负表示加速度方向;匀变速直线运动中,某段时间的平均速度等于初末速度之和的一半。
【解答】解:A.根据该无人机表演过程中在竖直方向运动的v﹣t图像可知,无人机在3s末前速度为正值,说明速度一直向上,所以无人机在3s末上升到最高点,故A错误;
B.v﹣t图像斜率表示加速度,由图知,无人机在3s时加速度不为0,故B错误;
C.无人机在1s末和5s末的斜率相同,所以加速度方向相同,故C错误;
D.无人机在0﹣2s的平均速度
,无人机在2s﹣3s的平均速度
所以无人机在0s﹣2s和2s﹣3s两个阶段的平均速度相等,故D正确。
故选:D。
【点评】解题关键是掌握v﹣t图像的物理意义,平均速度的公式。属于基础题。
8.(2024秋 渝中区校级期末)轨道摄影常用于田径比赛,即在最内侧跑道旁铺设固定的轨道,轨道上安装可沿轨道自由移动的高速摄像机,实现跟踪拍摄。在某次百米比赛中,摄像机和运动员的x﹣t图像如图所示,摄像机和运动员均可视为质点,下列说法中正确的是( )
A.摄像机做匀加速直线运动
B.t0时刻摄像机与运动员速度相同
C.0~t0时间内摄像机的平均速度大于运动员的平均速度
D.0~t0时间内摄像机与运动员的距离先变大后变小
【考点】利用x﹣t图像的斜率求解物体运动的速度;平均速度(定义式方向);根据x﹣t图像的物理意义对比多个物体的运动情况.
【专题】定性思想;图析法;运动学中的图象专题;理解能力.
【答案】D
【分析】x﹣t图像的形状反映了物体的位移随时间变化的情况,图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动,两条x﹣t图像的交点表示两个物体在某一时刻处于同一位置。
【解答】解:A.x﹣t图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动,可知摄像机做匀速直线运动,故A错误;
B.x﹣t图像的斜率表示速度,根据图像可知,t0时刻摄像机的速度小于运动员的速度,故B错误;
C.0~t0时间内摄像机的位移与运动员的位移大小相等,故平均速度相等,故C错误;
D.x﹣t图像始末位置相交,即始末位置相同,可知,0~t0时间内摄像机与运动员的距离先变大后变小,故D正确。
故选:D。
【点评】考查对x﹣t图像的理解,清楚图线的含义。
二.多选题(共4小题)
(多选)9.(2024秋 海口期末)如图所示,x﹣t图像中两条图线分别表示甲、乙两辆车由同一地点向同一方向运动的情况,下列说法正确的是( )
A.0~6s内,甲车的速度始终小于乙车的速度
B.0~6s内,甲车通过的路程等于乙车通过的路程
C.在6s末,甲、乙两车速度大小相同
D.在6s末,甲、乙两车位于同一位置
【考点】根据x﹣t图像的物理意义对比多个物体的运动情况.
【专题】定性思想;图析法;运动学中的图象专题;理解能力.
【答案】BD
【分析】x﹣t图像的形状反映了物体的位移随时间变化的情况,图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动,两条x﹣t图像的交点表示两个物体在某一时刻处于同一位置。
【解答】解:A.x﹣t图像斜率表示速度,开始时甲车的速度大于乙车的速度,故A错误;
B.由图像可知,0~6s内,甲车通过的路程等于乙车通过的路程,故B正确;
C.x﹣t图像斜率表示速度,在6s末,乙车速度大,故C错误;
D.由图像可知,在6s末,甲、乙两车位于同一位置,故D正确。
故选:BD。
【点评】考查对x﹣t图像的理解,清楚图线的含义。
(多选)10.(2024秋 水城区期末)0时刻可视为质点的汽车甲、乙在平行的相邻平直车道上并排行驶,两车运动的图像(横轴为时间t)如图所示,下列说法正确的是( )
A.当纵轴为位移(x)时,0~t1内汽车甲的平均速度小于汽车乙的平均速度
B.当纵轴为位移(x)时,0~t2内汽车甲的平均速度小于汽车乙的平均速度
C.当纵轴为速度(v)时,t1时刻甲的加速度大于乙的加速度
D.当纵轴为速度(v)时,t2时刻两车相遇
【考点】复杂的运动学图像问题;利用v﹣t图像与坐标轴围成的面积求物体的位移;利用v﹣t图像的斜率求解物体运动的加速度.
【专题】比较思想;图析法;运动学中的图象专题;理解能力.
【答案】AC
【分析】在x﹣t图像中,位移等于纵坐标的变化量,平均速度等于位移与时间之比;在v﹣t图像中,图线的斜率表示加速度,图像与横轴围成的面积表示位移,根据这些知识分析。
【解答】解:A、当纵轴为位移(x)时,位移等于纵坐标的变化量,由图像可知,0~t1内汽车甲的位移小于汽车乙的位移,根据可知,0~t1内汽车甲的平均速度小于汽车乙的平均速度,故A正确;
B、当纵轴为位移(x)时,由图像可知,0~t2内汽车甲的位移等于汽车乙的位移,根据可知,0~t2内汽车甲的平均速度等于汽车乙的平均速度,故B错误;
C、当纵轴为速度(v)时,根据v﹣t图像的斜率表示加速度,由图可知,t1时刻甲图线的斜率大于乙图线的斜率,则t1时刻甲的加速度大于乙的加速度,故C正确;
D、当纵轴为速度(v)时,根据v﹣t图像与横轴围成的面积表示位移,由图可知,0~t2时间内甲图线与横轴围成的面积小于乙图线与横轴围成的面积,则二者位移不等,由于二者起点并排行驶,所以t2时刻两车没有相遇,故D错误。
故选:AC。
【点评】解答本题时,要理解x﹣t图像和v﹣t图像的物理意义,知道在x﹣t图像中,位移等于纵坐标的变化量。在v﹣t图像中,图像与横轴围成的面积表示位移。要抓住它们的区别,不能混淆。
(多选)11.(2024秋 辽宁期末)下列描述直线运动的四个图像中,a为加速度,x为位移,v为速度,t为时间,其中B、D选项中的图像皆为抛物线,则所描述的运动一定是初速度为零的匀加速直线运动的是( )
A. B.
C. D.
【考点】多个类型的运动学图像综合问题;根据物体的运动情况判断v﹣t图像是否正确.
【专题】定性思想;推理法;运动学中的图象专题;推理论证能力.
【答案】BC
【分析】a﹣t图横轴围成的面积表示速度变化量;x﹣t图像可以得到位移;v﹣t图像中斜率表示加速度,初速度为零的匀加速直线v﹣t图应该是过原点的倾斜直线。
【解答】解:A.图像A中加速度不变,即匀变速直线运动,但初速度是否为零,是加速还是减速,都是不确定的,故A错误;
B.图像中相邻相同时间间隔的位移之比为1:3,因此,可以用来描述初速度为零的匀加速直线运动,故B正确;
C.由初速度为0的匀加速直线运动位移—时间关系可知x与成正比,所以C图像可以描述初速度为零的匀加速直线运动,故C正确;
D.由初速度为0的匀加速直线运动速度—时间关系y=at可见它的v﹣t图应该是过原点的倾斜直线,D图像是弯曲的,不可以描述匀加速直线运动,故D错误。
故选:BC。
【点评】本题考查了运动图像,理解运动图像中面积、斜率、坐标以及截距表示的含义是解决此类问题的关键。
(多选)12.(2024秋 红桥区期末)甲、乙两物体从同一点开始沿一直线运动,甲和乙的运动图像如图所示,下列说法中正确的是( )
A.甲、乙均做匀速直线运动
B.0~2s内与4~6s内,乙的加速度大小相等、方向相同
C.前3s内甲的平均速度为0,乙的平均速度为2m/s
D.甲、乙均在6s末回到出发点,距出发点的最大距离均为4m
【考点】利用v﹣t图像与坐标轴围成的面积求物体的位移;利用x﹣t图像的斜率求解物体运动的速度.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】BC
【分析】根据x﹣t图像的斜率表示速度,v﹣t图像与时间轴所围的面积表示位移,斜率表示加速度分析。
【解答】解:A.由乙的运动图像可知,甲做方向变化的匀速直线运动,乙做方向变化的匀变速直线运动,故A 错误;
B.因v﹣t图像的斜率等于加速度,可知在0~2s内与4~6s内,乙物体的加速度均为2m/s2,方向相同,故B正确;
C.前3s内,甲位移为0,所以平均速度为0,乙位移为
所以平均速度是
故C正确;
D.由甲和乙的运动图像可知,甲、乙均在6s末回到出发点,乙距离出发点的最大距离是
,甲距出发点的最大距离为4m,故D错误。
故选:BC。
【点评】对于运动图像,要注意看清图像的类别,理解x﹣t图像和v﹣t图像的物理意义,知道x﹣t图像的斜率表示速度,速度—时间图像与时间轴围成的面积大小表示位移大小。
三.填空题(共4小题)
13.(2024秋 叶县校级期末)探究物体自由落体运动规律
(1)物体做自由落体运动时 ABC 。
A.只受重力作用
B.运动为匀加速直线运动
C.运动的初速度为0
(2)下落速度v随时间t变化的图像为 D 。
(3)已知在月球表面,重力加速度为地球的。一小球在地球上离地面20m处静止释放,到达地球表面用时 2 s,在月球上离地面30m处静止释放,到达月球表面用时 6 s。若一小球在地球表面某一高度静止释放,用时t1,同一高度在月球表面用时t2,则 。(g=10m/s2)
【考点】自由落体运动的规律及应用;自由落体运动的定义、特点与判断.
【专题】定量思想;推理法;自由落体运动专题;理解能力.
【答案】(1)ABC;(2)D;(3)2,6,。
【分析】(1)(2)根据自由落体运动定义求解;
(3)根据自由落体运动列式求出时间,进行比较,得出结论。
【解答】解:(1)自由落体运动的初速度为零,物体只受重力,加速度不变,是匀加速直线运动,故ABC正确。
故选:ABC。
(2)自由落体运动的物体,加速度不变,恒为g,速度随时间均匀增大,故ABC错误,D正确。
故选:D。
(3)根据公式,得到达地球表面用时
同理可得,到达月球表面用时
若高度相同,则
故答案为:(1)ABC;(2)D;(3)2,6,。
【点评】本题考查的是自由落运动公式,其中主要考察的是自由落体运动的定义以及公式的应用。
14.(2024秋 闵行区期末)在高度180m处有两只气球(气球a和气球b),以相同速度10m/s分别匀速上升和匀速下降,此时,在这两只气球上各掉出一物体,则这两个物体落到地面时的时间差 2 s,所经过的路程差 10 m。(物体空气阻力不计)
【考点】竖直上抛运动的规律及应用;自由落体运动的规律及应用.
【专题】信息给予题;定量思想;推理法;自由落体运动专题;理解能力.
【答案】2;10。
【分析】根据竖直上抛运动规律求时间;根据匀加速运动规律求时间,再求时间差;根据运动学公式求做竖直上抛运动的物体的上升的最大高度,再求路程差。
【解答】解:随气球上升的物体离开气球后做竖直上抛运动,设落地时间为t1
取向下为正方向,根据竖直上抛运动规律:
随气球上升的物体离开气球后做匀加速直线运动,设落地时间为t2
取向下为正方向,根据
时间差Δt=t1﹣t2
代入数据联立解得:Δt=2s
做竖直上抛运动的物体,从抛出点上升的最大高度
两物体Δs=2H+h﹣h=2H=2×5m=10m
故答案为:2;10。
【点评】无论竖直上抛运动还是竖直下抛运动都是加速度a=g的匀变速直线运动;随气球上升的物体脱离气球时,并不会立即下落,要先向上做匀减速运动,到达最高点再下落。
15.(2023秋 龙岩期末)高空坠物现象被称为“悬在城市上空的痛”,已成为城市中仅次于交通事故的危险行为。试想一个花盆从高为20m的七楼窗台上坠落,忽略空气阻力,取g=10m/s2。花盆在空中下落的时间为 2 s;花盆落地时的速度为 20 m/s;花盆在最后1s内下落的距离为 15 m。
【考点】自由落体运动的规律及应用.
【专题】定量思想;方程法;自由落体运动专题;推理论证能力.
【答案】2;20;15。
【分析】根据自由落体运动的基本公式即可求解。
【解答】解:花盆做自由落体运动,则
解得花盆在空中下落的时间为t=2s
花盆落地时的速度为v=gt=2×10m/s=20m/s
花盆在最后1s内下落的距离为
代入数据得h1=15m
故答案为:2;20;15。
【点评】本题主要考查了自由落体运动的基本公式的直接应用,难度不大,属于基础题。
16.(2023秋 嘉兴期末)汽车A以vA=8m/s的速度做匀速直线运动,发现前方相距x0=14m处、以vB=20m/s的速度同向运动的汽车B正开始匀减速刹车,其刹车的加速度大小a=4m/s2。若汽车B速度减为零后保持静止,则从此刻开始计时,A追上B前,经过时间 3 s,A、B间的距离最远;经过时间 8 s,A恰好追上B。
【考点】匀速物体追变速物体问题.
【专题】定量思想;推理法;追及、相遇问题;理解能力.
【答案】3;8。
【分析】当两车速度相等时,两车距离最远;先判断前车静止时,后车是否追上,然后再进一步根据运动学公式列式求解。
【解答】解:A、B的速度相等时,两车的距离最远,则
vB﹣at=vA
解得
t=3s
B停止运动的时间为
此时A、B距离为
代入数据,解得
Δx=24m
则A追上B还需要的时间为
所以A追上B所需的时间为
t总=t1+t0=3s+5s=8s
故答案为:3;8。
【点评】本题是追击问题,要明确两车速度相等时,两车距离有极值;同时要先判断前车静止前量程能否相遇,然后根据运动学公式列式求解。
四.解答题(共4小题)
17.(2024秋 水城区期末)2024年8月18日,中国自主设计、自主集成的首台7000米级大深度载人潜水器“蛟龙号”完成了其第300次下潜。在一次模拟下潜中,潜水器(视为质点)由静止开始从海面上竖直向下做匀加速直线运动,下潜x1=160m时潜水器的速度大小v=8m/s,此后潜水器保持该速度匀速运动了t2=100s,最后做匀减速直线运动,下潜一段距离后速度恰好减为零,此时潜水器到水面的距离d=1040m。已知潜水器始终在同一竖直线上运动,求:
(1)潜水器做匀加速运动的加速度大小a1;
(2)潜水器做匀减速运动的加速度大小a2;
(3)潜水器这次下潜的总时间t。
【考点】匀变速直线运动规律的综合应用.
【专题】定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】(1)潜水器做匀加速运动的加速度大小a1等于0.2m/s2;
(2)潜水器做匀减速运动的加速度大小a1等于0.4m/s2;
(3)潜水器这次下潜的总时间等于160s。
【分析】(1)潜水器做匀加速直线运动,根据速度—位移关系求解加速度大小;
(2)求解潜水器做匀减速直线运动的位移,根据速度—位移关系求解加速度大小;
(3)根据速度—时间关系求解变速运动时间,三段时间相加等于总时间。
【解答】解:(1)潜水器做匀加速直线运动,有
v2=2a1x1
解得
(2)潜水器做匀速直线运动的位移大小
x2=vt2
潜水器做匀减速直线运动的位移大小
解得
(3)潜水器做匀加速直线运动的时间
做匀减速直线运动的时间
潜水器这次下潜的总时间
t=t1+t2+t3
解得
t=160s
答:(1)潜水器做匀加速运动的加速度大小a1等于0.2m/s2;
(2)潜水器做匀减速运动的加速度大小a2等于0.4m/s2;
(3)潜水器这次下潜的总时间t等于160s。
【点评】牛顿动力学问题是高考考查的重点,而与中国科技进步相关的高科技问题更能激起学生的爱国热情,本题借助最新的物理情景,考查了牛顿动力学问题,解题的关键是会将实际问题转换为物理模型。
18.(2024秋 水城区期末)如图所示,一辆货车在长坡路段下坡,刹车突然失灵,司机立即关闭发动机,货车以v0=30m/s的速度进入倾角θ=30°的斜面避险车道,滑行一段距离后停下。货车在斜面避险车道滑行的过程中受到空气和斜面的阻力,阻力大小恒为重力大小的,取重力加速度大小g=10m/s2,货车可视为质点。求:
(1)货车减速的加速度大小a;
(2)货车在斜面避险车道上滑行的时间t;
(3)货车在斜面避险车道上滑行的距离x。
【考点】匀变速直线运动速度与位移的关系;匀变速直线运动速度与时间的关系.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】(1)货车减速的加速度大小a为10m/s2;
(2)货车在斜面避险车道上滑行的时间t为3s;
(3)货车在斜面避险车道上滑行的距离x为45m。
【分析】(1)根据牛顿第二定律列式求解加速度大小;
(2)(3)根据匀变速直线运动的速度—时间规律和推论列式求解时间和位移。
【解答】解:(1)货车在斜面避险车道上滑行时,阻力fmg,根据牛顿第二定律有mgsin30°+f=ma,代入数据解得a=10m/s2;
(2)货车在斜面避险车道上做匀减速直线运动,由速度—时间规律有0=v0﹣at,解得t=3s;
(3)由匀变速直线运动的推论,货车在斜面避险车道上滑行的距离为,解得x=45m。
答:(1)货车减速的加速度大小a为10m/s2;
(2)货车在斜面避险车道上滑行的时间t为3s;
(3)货车在斜面避险车道上滑行的距离x为45m。
【点评】考查牛顿第二定律的应用以及匀变速直线运动的规律,会根据题意进行准确分析解答。
19.(2024秋 杭州期末)新能源汽车的智驾系统能够自主决策紧急制动。某新能源汽车在初速为108km/h紧急制动测试中,制动距离为x=45m。如图所示该车又进行自主决策紧急制动测试,待测车以v1=36km/h沿直线CO匀速行驶,车上智驾系统突然探测到“儿童”以v2=1.5m/s恒定速度从前方停靠车辆车头A处窜出沿直线AB运动,智驾系统感知分析后实施紧急制动。已知LAO=3.0m,LBO=1.5m,LCO=16m,汽车制动过程视为匀减速直线运动,“儿童”视为质点。
(1)求紧急制动过程中的加速度大小;
(2)已知该车智驾系统反应时间(从探测到“儿童”到实施紧急制动)Δt=0.2s,求该车停下时车头离O的距离;
(3)过早或频繁紧急制动不利于行车安全和驾乘舒适,若系统经过Δt=0.2s,未实施紧急制动,而是控制汽车在“儿童”到达路边B处时,车头恰好到达O点,则此次制动过程加速度为多大?
【考点】匀变速直线运动规律的综合应用.
【专题】计算题;定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】(1)紧急制动过程中的加速度大小为10m/s2;
(2)该车停下时车头离O的距离为9m;
(3)此次制动过程加速度为。
【分析】(1)根据求解紧急制动过程中的加速度大小;
(2)根据x=vt求解系统反应时间内汽车匀速运动距离,根据求解汽车匀减速距离,进而求得该车停下时车头离O的距离;
(3)根据x=vt求解)“儿童”匀速运动到B处时间,从而求得汽车匀减速时间,再根据求解此次制动过程加速度。
【解答】解:(1)汽车初速度v0=108km/h=30m/s,根据可得;
(2)系统反应时间内汽车匀速运动,Δt=0.2s,v1=36km/h=10m/s,匀速运动的距离为x1=v1 Δt=10×0.2m=2m,匀减速阶段,根据可得,车头离O点距离s=Lco﹣x1﹣x2=16m﹣2m﹣5m=9m;
(3)“儿童”做匀速运动,运动到B处时间为,汽车匀减速时间t2=t1﹣Δt=3.0s﹣0.2s=2.8s,根据可得,代入数据得,解得;
答:(1)紧急制动过程中的加速度大小为10m/s2;
(2)该车停下时车头离O的距离为9m;
(3)此次制动过程加速度为。
【点评】本题主要考查了匀变速直线运动的规律,可根据速度—位移公式、速度—时间公式等进行求解。
20.(2024秋 济宁期末)机器人某次在平台上运送货物时,从A处由静止出发沿两段互相垂直的直线路径AB、BC运动到C处停下。已知机器人最大运行速率vm=3m/s,加速或减速运动时的加速度大小均为a=2m/s2,A到B的时间tAB=3.5s,BC距离xBC=4.5m,机器人途经B处时的速率为零,忽略机器人在B处的转向时间。要求机器人最短时间内到达C处,运动过程中机器人可视为质点。求:
(1)AB间的距离xAB;
(2)机器人从A处运动到C处的平均速度大小(结果保留两位小数)。
【考点】匀变速直线运动中的平均速度的应用(平均速度的推论);匀变速直线运动速度与时间的关系;匀变速直线运动速度与位移的关系.
【专题】定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】(1)AB间的距离xAB等于6m;
(2)机器人从A处运动到C处的平均速度大小等于1.15m/s。
【分析】(1)机器人先加速再匀速,最后减速,求出三段时间的和即可;
(2)先求出从B到C的时间,再根据平均速度的定义式求出平均速度。
【解答】解:(1)设机器人从A到B过程中,加速到vm所需时间为t1,减速所用时间为t2,
则
机器人从A运动到B的过程,加速、减速运动的位移分别为x1、x2,
则
匀速运动的位移
x3=vm(tAB﹣t1﹣t2)
AB间的距离
xAB=x1+x2+x3
解的xAB=6m
(2)机器人从B运动到C的过程恰好达到最大速度vm,不经历匀速过程。
机器人从B运动到C的时间
tBC=t1+t2,解得tBC=3s
机器人从A运动到C的位移大小
从A运动到C的平均速度大小
解得
答:(1)AB间的距离xAB等于6m;
(2)机器人从A处运动到C处的平均速度大小等于1.15m/s。
【点评】在处理多过程问题时,要注意分析各过程的运动性质,再利用各自的运动规律解决问题,难度不大。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
高考物理考前冲刺押题预测 匀变速直线运动的研究
一.选择题(共8小题)
1.(2024秋 烟台期末)甲、乙两车在同一条平直公路上行驶,从t=0时刻起,甲车一直做匀速直线运动,乙车先做初速度为v0的匀加速直线运动,t1时刻接着做匀减速直线运动,t2时刻速度减为v,两车位移x随时间t变化的关系图像如图所示。已知t2=2t1,则关于v0和v的大小关系,下列说法正确的是( )
A.v0<v B.v0=v C.v0=2v D.v0=3v
2.(2024秋 榆林期末)某同学采用频闪摄影的方法拍摄到如图所示的小球做自由落体运动的照片,将一小球从高为hm处静止释放,重力加速度g取10m/s2,忽略空气阻力,该频闪摄影的闪光频率为( )
A.1Hz B.15Hz C.30Hz D.45Hz
3.(2024秋 湖北期末)在一次无人机飞行表演中,初始时刻两无人机从空中同一地点以相同的初速度v0=30m/s由西向东水平飞行。无人机甲安装有加速度传感器,无人机乙安装有速度传感器,选取向东为正方向,两无人机各自传感器读数与时间的关系图像如图所示。下列说法正确的是( )
A.3~9s内,甲向东飞行,乙向西飞行
B.3~9s内,甲的加速度与乙的加速度相同
C.9s末甲、乙相距45m
D.0~9s内甲的平均速度为0
4.(2024秋 盐城期末)乙同学为测量自己反应时间,进行了如下实验。如图所示,请甲同学用手捏住直尺,乙用一只手在直尺“0刻度”位置处做捏住直尺准备,在看到甲松手后,乙立刻捏住直尺,读出捏住直尺的刻度,即可算出自己反应时间。后期甲、乙同学又合作设计了一种测量反应时间的“反应时间测量尺”,如图所示,重力加速度g=10m/s2,以下说法正确的是( )
A.甲同学捏住直尺处的刻度值越大,其反应时间越短
B.尺子未竖直对实验结果没有影响
C.直尺刻度20cm处对应“反应时间测量尺”示数0.2s
D.直尺刻度40cm处对应“反应时间测量尺”示数0.4s
5.(2024秋 盐城期末)已知某物体做直线运动,其v﹣t图像如图所示,以下说法正确的是( )
A.前8s内位移为0
B.前8s内位移为12m
C.前4s的位移为12m
D.0~4s内加速度方向与4s~8s内加速度方向相反
6.(2024秋 石景山区期末)某物体位置随时间的关系为x=1+2t+3t2,则关于其速度与1s内的位移大小,下列说法正确的是( )
A.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为6m
B.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为6m
C.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为5m
D.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为5m
7.(2024秋 哈尔滨校级期末)如图甲所示是某无人机的飞行表演,图乙为该无人机表演过程中在竖直方向运动的v﹣t图像,以向上为正方向,下列说法正确的是( )
A.无人机在2s末上升到最高点
B.无人机在3s时加速度为0
C.无人机在1s末和5s末的加速度方向相反
D.无人机在0s﹣2s和2s﹣3s两个阶段的平均速度相等
8.(2024秋 渝中区校级期末)轨道摄影常用于田径比赛,即在最内侧跑道旁铺设固定的轨道,轨道上安装可沿轨道自由移动的高速摄像机,实现跟踪拍摄。在某次百米比赛中,摄像机和运动员的x﹣t图像如图所示,摄像机和运动员均可视为质点,下列说法中正确的是( )
A.摄像机做匀加速直线运动
B.t0时刻摄像机与运动员速度相同
C.0~t0时间内摄像机的平均速度大于运动员的平均速度
D.0~t0时间内摄像机与运动员的距离先变大后变小
二.多选题(共4小题)
(多选)9.(2024秋 海口期末)如图所示,x﹣t图像中两条图线分别表示甲、乙两辆车由同一地点向同一方向运动的情况,下列说法正确的是( )
A.0~6s内,甲车的速度始终小于乙车的速度
B.0~6s内,甲车通过的路程等于乙车通过的路程
C.在6s末,甲、乙两车速度大小相同
D.在6s末,甲、乙两车位于同一位置
(多选)10.(2024秋 水城区期末)0时刻可视为质点的汽车甲、乙在平行的相邻平直车道上并排行驶,两车运动的图像(横轴为时间t)如图所示,下列说法正确的是( )
A.当纵轴为位移(x)时,0~t1内汽车甲的平均速度小于汽车乙的平均速度
B.当纵轴为位移(x)时,0~t2内汽车甲的平均速度小于汽车乙的平均速度
C.当纵轴为速度(v)时,t1时刻甲的加速度大于乙的加速度
D.当纵轴为速度(v)时,t2时刻两车相遇
(多选)11.(2024秋 辽宁期末)下列描述直线运动的四个图像中,a为加速度,x为位移,v为速度,t为时间,其中B、D选项中的图像皆为抛物线,则所描述的运动一定是初速度为零的匀加速直线运动的是( )
A. B.
C. D.
(多选)12.(2024秋 红桥区期末)甲、乙两物体从同一点开始沿一直线运动,甲和乙的运动图像如图所示,下列说法中正确的是( )
A.甲、乙均做匀速直线运动
B.0~2s内与4~6s内,乙的加速度大小相等、方向相同
C.前3s内甲的平均速度为0,乙的平均速度为2m/s
D.甲、乙均在6s末回到出发点,距出发点的最大距离均为4m
三.填空题(共4小题)
13.(2024秋 叶县校级期末)探究物体自由落体运动规律
(1)物体做自由落体运动时 。
A.只受重力作用
B.运动为匀加速直线运动
C.运动的初速度为0
(2)下落速度v随时间t变化的图像为 。
(3)已知在月球表面,重力加速度为地球的。一小球在地球上离地面20m处静止释放,到达地球表面用时 s,在月球上离地面30m处静止释放,到达月球表面用时 s。若一小球在地球表面某一高度静止释放,用时t1,同一高度在月球表面用时t2,则 。(g=10m/s2)
14.(2024秋 闵行区期末)在高度180m处有两只气球(气球a和气球b),以相同速度10m/s分别匀速上升和匀速下降,此时,在这两只气球上各掉出一物体,则这两个物体落到地面时的时间差 s,所经过的路程差 m。(物体空气阻力不计)
15.(2023秋 龙岩期末)高空坠物现象被称为“悬在城市上空的痛”,已成为城市中仅次于交通事故的危险行为。试想一个花盆从高为20m的七楼窗台上坠落,忽略空气阻力,取g=10m/s2。花盆在空中下落的时间为 s;花盆落地时的速度为 m/s;花盆在最后1s内下落的距离为 m。
16.(2023秋 嘉兴期末)汽车A以vA=8m/s的速度做匀速直线运动,发现前方相距x0=14m处、以vB=20m/s的速度同向运动的汽车B正开始匀减速刹车,其刹车的加速度大小a=4m/s2。若汽车B速度减为零后保持静止,则从此刻开始计时,A追上B前,经过时间 s,A、B间的距离最远;经过时间 s,A恰好追上B。
四.解答题(共4小题)
17.(2024秋 水城区期末)2024年8月18日,中国自主设计、自主集成的首台7000米级大深度载人潜水器“蛟龙号”完成了其第300次下潜。在一次模拟下潜中,潜水器(视为质点)由静止开始从海面上竖直向下做匀加速直线运动,下潜x1=160m时潜水器的速度大小v=8m/s,此后潜水器保持该速度匀速运动了t2=100s,最后做匀减速直线运动,下潜一段距离后速度恰好减为零,此时潜水器到水面的距离d=1040m。已知潜水器始终在同一竖直线上运动,求:
(1)潜水器做匀加速运动的加速度大小a1;
(2)潜水器做匀减速运动的加速度大小a2;
(3)潜水器这次下潜的总时间t。
18.(2024秋 水城区期末)如图所示,一辆货车在长坡路段下坡,刹车突然失灵,司机立即关闭发动机,货车以v0=30m/s的速度进入倾角θ=30°的斜面避险车道,滑行一段距离后停下。货车在斜面避险车道滑行的过程中受到空气和斜面的阻力,阻力大小恒为重力大小的,取重力加速度大小g=10m/s2,货车可视为质点。求:
(1)货车减速的加速度大小a;
(2)货车在斜面避险车道上滑行的时间t;
(3)货车在斜面避险车道上滑行的距离x。
19.(2024秋 杭州期末)新能源汽车的智驾系统能够自主决策紧急制动。某新能源汽车在初速为108km/h紧急制动测试中,制动距离为x=45m。如图所示该车又进行自主决策紧急制动测试,待测车以v1=36km/h沿直线CO匀速行驶,车上智驾系统突然探测到“儿童”以v2=1.5m/s恒定速度从前方停靠车辆车头A处窜出沿直线AB运动,智驾系统感知分析后实施紧急制动。已知LAO=3.0m,LBO=1.5m,LCO=16m,汽车制动过程视为匀减速直线运动,“儿童”视为质点。
(1)求紧急制动过程中的加速度大小;
(2)已知该车智驾系统反应时间(从探测到“儿童”到实施紧急制动)Δt=0.2s,求该车停下时车头离O的距离;
(3)过早或频繁紧急制动不利于行车安全和驾乘舒适,若系统经过Δt=0.2s,未实施紧急制动,而是控制汽车在“儿童”到达路边B处时,车头恰好到达O点,则此次制动过程加速度为多大?
20.(2024秋 济宁期末)机器人某次在平台上运送货物时,从A处由静止出发沿两段互相垂直的直线路径AB、BC运动到C处停下。已知机器人最大运行速率vm=3m/s,加速或减速运动时的加速度大小均为a=2m/s2,A到B的时间tAB=3.5s,BC距离xBC=4.5m,机器人途经B处时的速率为零,忽略机器人在B处的转向时间。要求机器人最短时间内到达C处,运动过程中机器人可视为质点。求:
(1)AB间的距离xAB;
(2)机器人从A处运动到C处的平均速度大小(结果保留两位小数)。
高考物理考前冲刺押题预测 匀变速直线运动的研究
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 烟台期末)甲、乙两车在同一条平直公路上行驶,从t=0时刻起,甲车一直做匀速直线运动,乙车先做初速度为v0的匀加速直线运动,t1时刻接着做匀减速直线运动,t2时刻速度减为v,两车位移x随时间t变化的关系图像如图所示。已知t2=2t1,则关于v0和v的大小关系,下列说法正确的是( )
A.v0<v B.v0=v C.v0=2v D.v0=3v
【考点】根据x﹣t图像的物理意义对比多个物体的运动情况.
【专题】定性思想;图析法;运动学中的图象专题;理解能力.
【答案】B
【分析】x﹣t图像的形状反映了物体的位移随时间变化的情况,图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动。
【解答】解:x﹣t图像的斜率表示速度,根据图像可知,乙车两段时间内的平均速度相等,在匀变速直线运动中,平均速度等于初速度和末速度的算术平均值,t1时刻的速度为前段时间的末速度及后段时间的初速度,两者相等,则v0=v,故B正确,ACD错误。
故选:B。
【点评】考查对x﹣t图像的理解,清楚图线的含义。
2.(2024秋 榆林期末)某同学采用频闪摄影的方法拍摄到如图所示的小球做自由落体运动的照片,将一小球从高为hm处静止释放,重力加速度g取10m/s2,忽略空气阻力,该频闪摄影的闪光频率为( )
A.1Hz B.15Hz C.30Hz D.45Hz
【考点】频闪照相法求解自由落体运动.
【专题】定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】B
【分析】根据自由落体运动的位移—时间规律列式求解闪光周期以及频率。
【解答】解:设频闪周期为T,则根据自由落体运动规律有hg(5T)2,代入数据解得Ts,则闪光频率f,解得f=15Hz,故B正确,ACD错误。
故选:B。
【点评】考查自由落体运动的相关规律,会根据题意进行准确分析解答。
3.(2024秋 湖北期末)在一次无人机飞行表演中,初始时刻两无人机从空中同一地点以相同的初速度v0=30m/s由西向东水平飞行。无人机甲安装有加速度传感器,无人机乙安装有速度传感器,选取向东为正方向,两无人机各自传感器读数与时间的关系图像如图所示。下列说法正确的是( )
A.3~9s内,甲向东飞行,乙向西飞行
B.3~9s内,甲的加速度与乙的加速度相同
C.9s末甲、乙相距45m
D.0~9s内甲的平均速度为0
【考点】根据a﹣t图像的物理意义分析物体的运动情况;根据x﹣t图像的物理意义分析单个物体的运动情况.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】C
【分析】由a﹣t图像可以得出甲的加速度变化情况,结合匀变速运动规律求解;v﹣t图像斜率表示加速度,v﹣t图像面积表示位移。
【解答】解:A.3~9s内,乙速度一直为正,向东为正方向,故乙向东飞行,故A错误;
B.v﹣t图像斜率表示加速度,3~9s内,甲的加速度为正,乙的加速度为负,二者方向不同,故B错误;
CD.初速度v0=30m/s,由左图可知,前3s,加速度刚好减为零,位移x1,后面6s,加速运动x2,9s末甲
总位移x甲=x1+x2,解得x甲=135m,0~9s内甲的平均速度一定大于0;v﹣t图像面积表示位移,x乙30m=180m,9s末甲、乙相距180m﹣135m=45m,故C正确,D错误。
故选:C。
【点评】运动类图像问题关键是理解图像的物理意义。
4.(2024秋 盐城期末)乙同学为测量自己反应时间,进行了如下实验。如图所示,请甲同学用手捏住直尺,乙用一只手在直尺“0刻度”位置处做捏住直尺准备,在看到甲松手后,乙立刻捏住直尺,读出捏住直尺的刻度,即可算出自己反应时间。后期甲、乙同学又合作设计了一种测量反应时间的“反应时间测量尺”,如图所示,重力加速度g=10m/s2,以下说法正确的是( )
A.甲同学捏住直尺处的刻度值越大,其反应时间越短
B.尺子未竖直对实验结果没有影响
C.直尺刻度20cm处对应“反应时间测量尺”示数0.2s
D.直尺刻度40cm处对应“反应时间测量尺”示数0.4s
【考点】自由落体运动的规律及应用.
【专题】定量思想;推理法;自由落体运动专题;推理论证能力.
【答案】C
【分析】自由落体时间越长下落的高度越大,由于是匀变速直线运动所以相等的时间下落的高度不同,高度决定时间。
【解答】解:A.乙同学捏住直尺处的刻度值越大,下落的高度越大则反应时间越长,故A错误;
B.如果尺子未竖直,那么直尺下落时速度不能保持一直竖直向下,而且相对来说空气阻力会更大,刻度尺的下落不能近似看成自由落体运动,故B错误;
CD.若乙同学捏住直尺处的刻度值为20cm,根据公式:,则20cm处标注的时间刻度是:,同理40cm处标注的时间刻度是0.2s,不是0.4s,故C正确,D错误。
故选:C。
【点评】本题考查自由落体公式的基本应用,难度适中。
5.(2024秋 盐城期末)已知某物体做直线运动,其v﹣t图像如图所示,以下说法正确的是( )
A.前8s内位移为0
B.前8s内位移为12m
C.前4s的位移为12m
D.0~4s内加速度方向与4s~8s内加速度方向相反
【考点】利用v﹣t图像与坐标轴围成的面积求物体的位移;利用v﹣t图像的斜率求解物体运动的加速度;根据v﹣t图像的物理意义分析单个物体的运动情况.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】A
【分析】v﹣t图像反映了做直线运动的物体的速度随时间变化的规律,斜率表示加速度的大小及方向,图线与时间轴所包围的“面积”表示位移。
【解答】解:AB.v﹣t图线与时间轴所包围的“面积”表示位移,由图可得,前8s内图像在t轴上方和下方的面积相等,前8s内位移为0,故A正确,B错误;
C.v﹣t图线与时间轴所包围的“面积”表示位移,由图可得,前4s的位移为6m,故C错误;
D.v﹣t图像斜率表示加速度的大小及方向,0~4s内加速度方向与4s~8s内加速度方向相同,故D错误。
故选:A。
【点评】考查对v﹣t图像的理解,清楚图线的含义。
6.(2024秋 石景山区期末)某物体位置随时间的关系为x=1+2t+3t2,则关于其速度与1s内的位移大小,下列说法正确的是( )
A.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为6m
B.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为6m
C.速度是刻画物体位置变化快慢的物理量,1s内的位移大小为5m
D.速度是刻画物体位移变化快慢的物理量,1s内的位移大小为5m
【考点】匀变速直线运动位移与时间的关系.
【专题】定量思想;推理法;直线运动规律专题;理解能力.
【答案】C
【分析】根据速度的概念分析速度的物理意义。先确定t=0时刻与t=1s时刻物体的位置,由位置的变化得到位移的大小。
【解答】解:速度是描述物体运动快慢的物理量,运动对应空间位置变化,故速度是描述位置变化快慢的物理量。
物体位置随时间的关系为x=1+2t+3t2(m),则可得t=0时刻,物体位置为x0=1m,t=1s时刻,物体位置为x1=6m
故1s内物体的位移大小为:Δx=x1﹣x0=6m﹣1m=5m,故ABD错误,C正确。
故选:C。
【点评】本题考查学生对速度概念的理解,速度的定义是位移与时间的比值,而位移是物体位置的变化,故速度是刻画物体位置变化快慢的物理量。
7.(2024秋 哈尔滨校级期末)如图甲所示是某无人机的飞行表演,图乙为该无人机表演过程中在竖直方向运动的v﹣t图像,以向上为正方向,下列说法正确的是( )
A.无人机在2s末上升到最高点
B.无人机在3s时加速度为0
C.无人机在1s末和5s末的加速度方向相反
D.无人机在0s﹣2s和2s﹣3s两个阶段的平均速度相等
【考点】利用v﹣t图像的斜率求解物体运动的加速度;利用v﹣t图像与坐标轴围成的面积求物体的位移.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】D
【分析】v﹣t图像的斜率表示加速度,斜率大小表示加速度大小,斜率正负表示加速度方向;匀变速直线运动中,某段时间的平均速度等于初末速度之和的一半。
【解答】解:A.根据该无人机表演过程中在竖直方向运动的v﹣t图像可知,无人机在3s末前速度为正值,说明速度一直向上,所以无人机在3s末上升到最高点,故A错误;
B.v﹣t图像斜率表示加速度,由图知,无人机在3s时加速度不为0,故B错误;
C.无人机在1s末和5s末的斜率相同,所以加速度方向相同,故C错误;
D.无人机在0﹣2s的平均速度
,无人机在2s﹣3s的平均速度
所以无人机在0s﹣2s和2s﹣3s两个阶段的平均速度相等,故D正确。
故选:D。
【点评】解题关键是掌握v﹣t图像的物理意义,平均速度的公式。属于基础题。
8.(2024秋 渝中区校级期末)轨道摄影常用于田径比赛,即在最内侧跑道旁铺设固定的轨道,轨道上安装可沿轨道自由移动的高速摄像机,实现跟踪拍摄。在某次百米比赛中,摄像机和运动员的x﹣t图像如图所示,摄像机和运动员均可视为质点,下列说法中正确的是( )
A.摄像机做匀加速直线运动
B.t0时刻摄像机与运动员速度相同
C.0~t0时间内摄像机的平均速度大于运动员的平均速度
D.0~t0时间内摄像机与运动员的距离先变大后变小
【考点】利用x﹣t图像的斜率求解物体运动的速度;平均速度(定义式方向);根据x﹣t图像的物理意义对比多个物体的运动情况.
【专题】定性思想;图析法;运动学中的图象专题;理解能力.
【答案】D
【分析】x﹣t图像的形状反映了物体的位移随时间变化的情况,图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动,两条x﹣t图像的交点表示两个物体在某一时刻处于同一位置。
【解答】解:A.x﹣t图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动,可知摄像机做匀速直线运动,故A错误;
B.x﹣t图像的斜率表示速度,根据图像可知,t0时刻摄像机的速度小于运动员的速度,故B错误;
C.0~t0时间内摄像机的位移与运动员的位移大小相等,故平均速度相等,故C错误;
D.x﹣t图像始末位置相交,即始末位置相同,可知,0~t0时间内摄像机与运动员的距离先变大后变小,故D正确。
故选:D。
【点评】考查对x﹣t图像的理解,清楚图线的含义。
二.多选题(共4小题)
(多选)9.(2024秋 海口期末)如图所示,x﹣t图像中两条图线分别表示甲、乙两辆车由同一地点向同一方向运动的情况,下列说法正确的是( )
A.0~6s内,甲车的速度始终小于乙车的速度
B.0~6s内,甲车通过的路程等于乙车通过的路程
C.在6s末,甲、乙两车速度大小相同
D.在6s末,甲、乙两车位于同一位置
【考点】根据x﹣t图像的物理意义对比多个物体的运动情况.
【专题】定性思想;图析法;运动学中的图象专题;理解能力.
【答案】BD
【分析】x﹣t图像的形状反映了物体的位移随时间变化的情况,图像的斜率表示速度,倾斜的直线表示物体做匀速直线运动,曲线则表示物体做变速直线运动,两条x﹣t图像的交点表示两个物体在某一时刻处于同一位置。
【解答】解:A.x﹣t图像斜率表示速度,开始时甲车的速度大于乙车的速度,故A错误;
B.由图像可知,0~6s内,甲车通过的路程等于乙车通过的路程,故B正确;
C.x﹣t图像斜率表示速度,在6s末,乙车速度大,故C错误;
D.由图像可知,在6s末,甲、乙两车位于同一位置,故D正确。
故选:BD。
【点评】考查对x﹣t图像的理解,清楚图线的含义。
(多选)10.(2024秋 水城区期末)0时刻可视为质点的汽车甲、乙在平行的相邻平直车道上并排行驶,两车运动的图像(横轴为时间t)如图所示,下列说法正确的是( )
A.当纵轴为位移(x)时,0~t1内汽车甲的平均速度小于汽车乙的平均速度
B.当纵轴为位移(x)时,0~t2内汽车甲的平均速度小于汽车乙的平均速度
C.当纵轴为速度(v)时,t1时刻甲的加速度大于乙的加速度
D.当纵轴为速度(v)时,t2时刻两车相遇
【考点】复杂的运动学图像问题;利用v﹣t图像与坐标轴围成的面积求物体的位移;利用v﹣t图像的斜率求解物体运动的加速度.
【专题】比较思想;图析法;运动学中的图象专题;理解能力.
【答案】AC
【分析】在x﹣t图像中,位移等于纵坐标的变化量,平均速度等于位移与时间之比;在v﹣t图像中,图线的斜率表示加速度,图像与横轴围成的面积表示位移,根据这些知识分析。
【解答】解:A、当纵轴为位移(x)时,位移等于纵坐标的变化量,由图像可知,0~t1内汽车甲的位移小于汽车乙的位移,根据可知,0~t1内汽车甲的平均速度小于汽车乙的平均速度,故A正确;
B、当纵轴为位移(x)时,由图像可知,0~t2内汽车甲的位移等于汽车乙的位移,根据可知,0~t2内汽车甲的平均速度等于汽车乙的平均速度,故B错误;
C、当纵轴为速度(v)时,根据v﹣t图像的斜率表示加速度,由图可知,t1时刻甲图线的斜率大于乙图线的斜率,则t1时刻甲的加速度大于乙的加速度,故C正确;
D、当纵轴为速度(v)时,根据v﹣t图像与横轴围成的面积表示位移,由图可知,0~t2时间内甲图线与横轴围成的面积小于乙图线与横轴围成的面积,则二者位移不等,由于二者起点并排行驶,所以t2时刻两车没有相遇,故D错误。
故选:AC。
【点评】解答本题时,要理解x﹣t图像和v﹣t图像的物理意义,知道在x﹣t图像中,位移等于纵坐标的变化量。在v﹣t图像中,图像与横轴围成的面积表示位移。要抓住它们的区别,不能混淆。
(多选)11.(2024秋 辽宁期末)下列描述直线运动的四个图像中,a为加速度,x为位移,v为速度,t为时间,其中B、D选项中的图像皆为抛物线,则所描述的运动一定是初速度为零的匀加速直线运动的是( )
A. B.
C. D.
【考点】多个类型的运动学图像综合问题;根据物体的运动情况判断v﹣t图像是否正确.
【专题】定性思想;推理法;运动学中的图象专题;推理论证能力.
【答案】BC
【分析】a﹣t图横轴围成的面积表示速度变化量;x﹣t图像可以得到位移;v﹣t图像中斜率表示加速度,初速度为零的匀加速直线v﹣t图应该是过原点的倾斜直线。
【解答】解:A.图像A中加速度不变,即匀变速直线运动,但初速度是否为零,是加速还是减速,都是不确定的,故A错误;
B.图像中相邻相同时间间隔的位移之比为1:3,因此,可以用来描述初速度为零的匀加速直线运动,故B正确;
C.由初速度为0的匀加速直线运动位移—时间关系可知x与成正比,所以C图像可以描述初速度为零的匀加速直线运动,故C正确;
D.由初速度为0的匀加速直线运动速度—时间关系y=at可见它的v﹣t图应该是过原点的倾斜直线,D图像是弯曲的,不可以描述匀加速直线运动,故D错误。
故选:BC。
【点评】本题考查了运动图像,理解运动图像中面积、斜率、坐标以及截距表示的含义是解决此类问题的关键。
(多选)12.(2024秋 红桥区期末)甲、乙两物体从同一点开始沿一直线运动,甲和乙的运动图像如图所示,下列说法中正确的是( )
A.甲、乙均做匀速直线运动
B.0~2s内与4~6s内,乙的加速度大小相等、方向相同
C.前3s内甲的平均速度为0,乙的平均速度为2m/s
D.甲、乙均在6s末回到出发点,距出发点的最大距离均为4m
【考点】利用v﹣t图像与坐标轴围成的面积求物体的位移;利用x﹣t图像的斜率求解物体运动的速度.
【专题】定量思想;推理法;运动学中的图象专题;推理论证能力.
【答案】BC
【分析】根据x﹣t图像的斜率表示速度,v﹣t图像与时间轴所围的面积表示位移,斜率表示加速度分析。
【解答】解:A.由乙的运动图像可知,甲做方向变化的匀速直线运动,乙做方向变化的匀变速直线运动,故A 错误;
B.因v﹣t图像的斜率等于加速度,可知在0~2s内与4~6s内,乙物体的加速度均为2m/s2,方向相同,故B正确;
C.前3s内,甲位移为0,所以平均速度为0,乙位移为
所以平均速度是
故C正确;
D.由甲和乙的运动图像可知,甲、乙均在6s末回到出发点,乙距离出发点的最大距离是
,甲距出发点的最大距离为4m,故D错误。
故选:BC。
【点评】对于运动图像,要注意看清图像的类别,理解x﹣t图像和v﹣t图像的物理意义,知道x﹣t图像的斜率表示速度,速度—时间图像与时间轴围成的面积大小表示位移大小。
三.填空题(共4小题)
13.(2024秋 叶县校级期末)探究物体自由落体运动规律
(1)物体做自由落体运动时 ABC 。
A.只受重力作用
B.运动为匀加速直线运动
C.运动的初速度为0
(2)下落速度v随时间t变化的图像为 D 。
(3)已知在月球表面,重力加速度为地球的。一小球在地球上离地面20m处静止释放,到达地球表面用时 2 s,在月球上离地面30m处静止释放,到达月球表面用时 6 s。若一小球在地球表面某一高度静止释放,用时t1,同一高度在月球表面用时t2,则 。(g=10m/s2)
【考点】自由落体运动的规律及应用;自由落体运动的定义、特点与判断.
【专题】定量思想;推理法;自由落体运动专题;理解能力.
【答案】(1)ABC;(2)D;(3)2,6,。
【分析】(1)(2)根据自由落体运动定义求解;
(3)根据自由落体运动列式求出时间,进行比较,得出结论。
【解答】解:(1)自由落体运动的初速度为零,物体只受重力,加速度不变,是匀加速直线运动,故ABC正确。
故选:ABC。
(2)自由落体运动的物体,加速度不变,恒为g,速度随时间均匀增大,故ABC错误,D正确。
故选:D。
(3)根据公式,得到达地球表面用时
同理可得,到达月球表面用时
若高度相同,则
故答案为:(1)ABC;(2)D;(3)2,6,。
【点评】本题考查的是自由落运动公式,其中主要考察的是自由落体运动的定义以及公式的应用。
14.(2024秋 闵行区期末)在高度180m处有两只气球(气球a和气球b),以相同速度10m/s分别匀速上升和匀速下降,此时,在这两只气球上各掉出一物体,则这两个物体落到地面时的时间差 2 s,所经过的路程差 10 m。(物体空气阻力不计)
【考点】竖直上抛运动的规律及应用;自由落体运动的规律及应用.
【专题】信息给予题;定量思想;推理法;自由落体运动专题;理解能力.
【答案】2;10。
【分析】根据竖直上抛运动规律求时间;根据匀加速运动规律求时间,再求时间差;根据运动学公式求做竖直上抛运动的物体的上升的最大高度,再求路程差。
【解答】解:随气球上升的物体离开气球后做竖直上抛运动,设落地时间为t1
取向下为正方向,根据竖直上抛运动规律:
随气球上升的物体离开气球后做匀加速直线运动,设落地时间为t2
取向下为正方向,根据
时间差Δt=t1﹣t2
代入数据联立解得:Δt=2s
做竖直上抛运动的物体,从抛出点上升的最大高度
两物体Δs=2H+h﹣h=2H=2×5m=10m
故答案为:2;10。
【点评】无论竖直上抛运动还是竖直下抛运动都是加速度a=g的匀变速直线运动;随气球上升的物体脱离气球时,并不会立即下落,要先向上做匀减速运动,到达最高点再下落。
15.(2023秋 龙岩期末)高空坠物现象被称为“悬在城市上空的痛”,已成为城市中仅次于交通事故的危险行为。试想一个花盆从高为20m的七楼窗台上坠落,忽略空气阻力,取g=10m/s2。花盆在空中下落的时间为 2 s;花盆落地时的速度为 20 m/s;花盆在最后1s内下落的距离为 15 m。
【考点】自由落体运动的规律及应用.
【专题】定量思想;方程法;自由落体运动专题;推理论证能力.
【答案】2;20;15。
【分析】根据自由落体运动的基本公式即可求解。
【解答】解:花盆做自由落体运动,则
解得花盆在空中下落的时间为t=2s
花盆落地时的速度为v=gt=2×10m/s=20m/s
花盆在最后1s内下落的距离为
代入数据得h1=15m
故答案为:2;20;15。
【点评】本题主要考查了自由落体运动的基本公式的直接应用,难度不大,属于基础题。
16.(2023秋 嘉兴期末)汽车A以vA=8m/s的速度做匀速直线运动,发现前方相距x0=14m处、以vB=20m/s的速度同向运动的汽车B正开始匀减速刹车,其刹车的加速度大小a=4m/s2。若汽车B速度减为零后保持静止,则从此刻开始计时,A追上B前,经过时间 3 s,A、B间的距离最远;经过时间 8 s,A恰好追上B。
【考点】匀速物体追变速物体问题.
【专题】定量思想;推理法;追及、相遇问题;理解能力.
【答案】3;8。
【分析】当两车速度相等时,两车距离最远;先判断前车静止时,后车是否追上,然后再进一步根据运动学公式列式求解。
【解答】解:A、B的速度相等时,两车的距离最远,则
vB﹣at=vA
解得
t=3s
B停止运动的时间为
此时A、B距离为
代入数据,解得
Δx=24m
则A追上B还需要的时间为
所以A追上B所需的时间为
t总=t1+t0=3s+5s=8s
故答案为:3;8。
【点评】本题是追击问题,要明确两车速度相等时,两车距离有极值;同时要先判断前车静止前量程能否相遇,然后根据运动学公式列式求解。
四.解答题(共4小题)
17.(2024秋 水城区期末)2024年8月18日,中国自主设计、自主集成的首台7000米级大深度载人潜水器“蛟龙号”完成了其第300次下潜。在一次模拟下潜中,潜水器(视为质点)由静止开始从海面上竖直向下做匀加速直线运动,下潜x1=160m时潜水器的速度大小v=8m/s,此后潜水器保持该速度匀速运动了t2=100s,最后做匀减速直线运动,下潜一段距离后速度恰好减为零,此时潜水器到水面的距离d=1040m。已知潜水器始终在同一竖直线上运动,求:
(1)潜水器做匀加速运动的加速度大小a1;
(2)潜水器做匀减速运动的加速度大小a2;
(3)潜水器这次下潜的总时间t。
【考点】匀变速直线运动规律的综合应用.
【专题】定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】(1)潜水器做匀加速运动的加速度大小a1等于0.2m/s2;
(2)潜水器做匀减速运动的加速度大小a1等于0.4m/s2;
(3)潜水器这次下潜的总时间等于160s。
【分析】(1)潜水器做匀加速直线运动,根据速度—位移关系求解加速度大小;
(2)求解潜水器做匀减速直线运动的位移,根据速度—位移关系求解加速度大小;
(3)根据速度—时间关系求解变速运动时间,三段时间相加等于总时间。
【解答】解:(1)潜水器做匀加速直线运动,有
v2=2a1x1
解得
(2)潜水器做匀速直线运动的位移大小
x2=vt2
潜水器做匀减速直线运动的位移大小
解得
(3)潜水器做匀加速直线运动的时间
做匀减速直线运动的时间
潜水器这次下潜的总时间
t=t1+t2+t3
解得
t=160s
答:(1)潜水器做匀加速运动的加速度大小a1等于0.2m/s2;
(2)潜水器做匀减速运动的加速度大小a2等于0.4m/s2;
(3)潜水器这次下潜的总时间t等于160s。
【点评】牛顿动力学问题是高考考查的重点,而与中国科技进步相关的高科技问题更能激起学生的爱国热情,本题借助最新的物理情景,考查了牛顿动力学问题,解题的关键是会将实际问题转换为物理模型。
18.(2024秋 水城区期末)如图所示,一辆货车在长坡路段下坡,刹车突然失灵,司机立即关闭发动机,货车以v0=30m/s的速度进入倾角θ=30°的斜面避险车道,滑行一段距离后停下。货车在斜面避险车道滑行的过程中受到空气和斜面的阻力,阻力大小恒为重力大小的,取重力加速度大小g=10m/s2,货车可视为质点。求:
(1)货车减速的加速度大小a;
(2)货车在斜面避险车道上滑行的时间t;
(3)货车在斜面避险车道上滑行的距离x。
【考点】匀变速直线运动速度与位移的关系;匀变速直线运动速度与时间的关系.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】(1)货车减速的加速度大小a为10m/s2;
(2)货车在斜面避险车道上滑行的时间t为3s;
(3)货车在斜面避险车道上滑行的距离x为45m。
【分析】(1)根据牛顿第二定律列式求解加速度大小;
(2)(3)根据匀变速直线运动的速度—时间规律和推论列式求解时间和位移。
【解答】解:(1)货车在斜面避险车道上滑行时,阻力fmg,根据牛顿第二定律有mgsin30°+f=ma,代入数据解得a=10m/s2;
(2)货车在斜面避险车道上做匀减速直线运动,由速度—时间规律有0=v0﹣at,解得t=3s;
(3)由匀变速直线运动的推论,货车在斜面避险车道上滑行的距离为,解得x=45m。
答:(1)货车减速的加速度大小a为10m/s2;
(2)货车在斜面避险车道上滑行的时间t为3s;
(3)货车在斜面避险车道上滑行的距离x为45m。
【点评】考查牛顿第二定律的应用以及匀变速直线运动的规律,会根据题意进行准确分析解答。
19.(2024秋 杭州期末)新能源汽车的智驾系统能够自主决策紧急制动。某新能源汽车在初速为108km/h紧急制动测试中,制动距离为x=45m。如图所示该车又进行自主决策紧急制动测试,待测车以v1=36km/h沿直线CO匀速行驶,车上智驾系统突然探测到“儿童”以v2=1.5m/s恒定速度从前方停靠车辆车头A处窜出沿直线AB运动,智驾系统感知分析后实施紧急制动。已知LAO=3.0m,LBO=1.5m,LCO=16m,汽车制动过程视为匀减速直线运动,“儿童”视为质点。
(1)求紧急制动过程中的加速度大小;
(2)已知该车智驾系统反应时间(从探测到“儿童”到实施紧急制动)Δt=0.2s,求该车停下时车头离O的距离;
(3)过早或频繁紧急制动不利于行车安全和驾乘舒适,若系统经过Δt=0.2s,未实施紧急制动,而是控制汽车在“儿童”到达路边B处时,车头恰好到达O点,则此次制动过程加速度为多大?
【考点】匀变速直线运动规律的综合应用.
【专题】计算题;定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】(1)紧急制动过程中的加速度大小为10m/s2;
(2)该车停下时车头离O的距离为9m;
(3)此次制动过程加速度为。
【分析】(1)根据求解紧急制动过程中的加速度大小;
(2)根据x=vt求解系统反应时间内汽车匀速运动距离,根据求解汽车匀减速距离,进而求得该车停下时车头离O的距离;
(3)根据x=vt求解)“儿童”匀速运动到B处时间,从而求得汽车匀减速时间,再根据求解此次制动过程加速度。
【解答】解:(1)汽车初速度v0=108km/h=30m/s,根据可得;
(2)系统反应时间内汽车匀速运动,Δt=0.2s,v1=36km/h=10m/s,匀速运动的距离为x1=v1 Δt=10×0.2m=2m,匀减速阶段,根据可得,车头离O点距离s=Lco﹣x1﹣x2=16m﹣2m﹣5m=9m;
(3)“儿童”做匀速运动,运动到B处时间为,汽车匀减速时间t2=t1﹣Δt=3.0s﹣0.2s=2.8s,根据可得,代入数据得,解得;
答:(1)紧急制动过程中的加速度大小为10m/s2;
(2)该车停下时车头离O的距离为9m;
(3)此次制动过程加速度为。
【点评】本题主要考查了匀变速直线运动的规律,可根据速度—位移公式、速度—时间公式等进行求解。
20.(2024秋 济宁期末)机器人某次在平台上运送货物时,从A处由静止出发沿两段互相垂直的直线路径AB、BC运动到C处停下。已知机器人最大运行速率vm=3m/s,加速或减速运动时的加速度大小均为a=2m/s2,A到B的时间tAB=3.5s,BC距离xBC=4.5m,机器人途经B处时的速率为零,忽略机器人在B处的转向时间。要求机器人最短时间内到达C处,运动过程中机器人可视为质点。求:
(1)AB间的距离xAB;
(2)机器人从A处运动到C处的平均速度大小(结果保留两位小数)。
【考点】匀变速直线运动中的平均速度的应用(平均速度的推论);匀变速直线运动速度与时间的关系;匀变速直线运动速度与位移的关系.
【专题】定量思想;推理法;直线运动规律专题;推理论证能力.
【答案】(1)AB间的距离xAB等于6m;
(2)机器人从A处运动到C处的平均速度大小等于1.15m/s。
【分析】(1)机器人先加速再匀速,最后减速,求出三段时间的和即可;
(2)先求出从B到C的时间,再根据平均速度的定义式求出平均速度。
【解答】解:(1)设机器人从A到B过程中,加速到vm所需时间为t1,减速所用时间为t2,
则
机器人从A运动到B的过程,加速、减速运动的位移分别为x1、x2,
则
匀速运动的位移
x3=vm(tAB﹣t1﹣t2)
AB间的距离
xAB=x1+x2+x3
解的xAB=6m
(2)机器人从B运动到C的过程恰好达到最大速度vm,不经历匀速过程。
机器人从B运动到C的时间
tBC=t1+t2,解得tBC=3s
机器人从A运动到C的位移大小
从A运动到C的平均速度大小
解得
答:(1)AB间的距离xAB等于6m;
(2)机器人从A处运动到C处的平均速度大小等于1.15m/s。
【点评】在处理多过程问题时,要注意分析各过程的运动性质,再利用各自的运动规律解决问题,难度不大。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
