20.1.1 第2课时 用样本平均数估计总体平均数 课件(共31张PPT)
文档属性
| 名称 | 20.1.1 第2课时 用样本平均数估计总体平均数 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 14:57:42 | ||
图片预览










文档简介
(共31张PPT)
人教版数学八年级下册
第二十章 数据的分析
汇报人:孙老师
汇报班级:X级X班
20.1.1 第2课时 用样本平均数估计总体平均数
20.1 数据的集中趋势
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解加权平均数的概念.
2.会计算加权平均数并体会权的重要性.
3.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.
第贰章节
新课导入
新课导入
简单随机抽样:
一般地,设一个总体含有N (N为正整数)个个体,从中逐个抽取n (1步骤 优点 缺点
抽签法 ①编号; ②制签、抽签; ③得样本. 简单易行 总体较大时操作麻烦,效果不好.
随机数法 ①编号; ②产生随机数; ③得样本. 简单易行 总体特别大时,不方便.
第叁章节
新知探究
新知探究
知识点1: 组中值与平均数
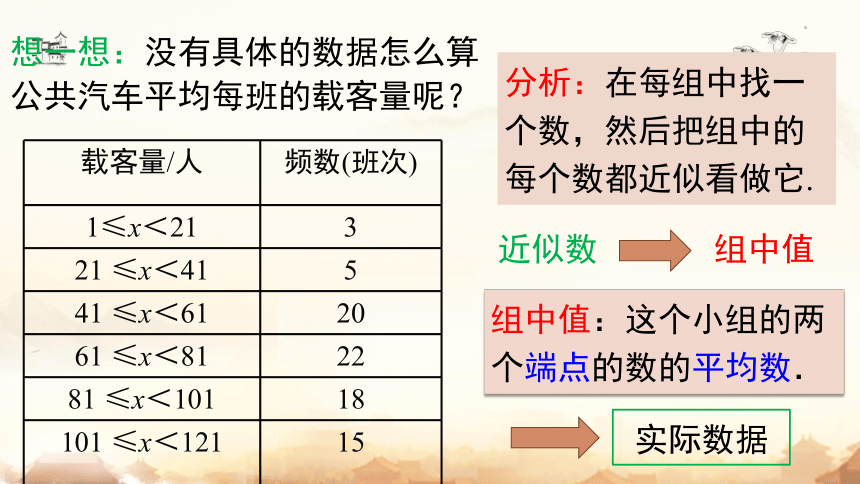
问题1:为了解 5 路公共汽车的运营情况,公交部门统计了某天 5 路公共汽车每个运行班次的载客量,得到下表,这天 5 路公共汽车平均每班的载客量是多少?
载客量/人 频数(班次)
1≤x<21 3
21 ≤x<41 5
41 ≤x<61 20
61 ≤x<81 22
81 ≤x<101 18
101 ≤x<121 15
载客量/人 频数(班次)
1≤x<21 3
21 ≤x<41 5
41 ≤x<61 20
61 ≤x<81 22
81 ≤x<101 18
101 ≤x<121 15
想一想:没有具体的数据怎么算公共汽车平均每班的载客量呢?
分析:在每组中找一个数,然后把组中的每个数都近似看做它.
组中值
近似数
组中值:这个小组的两个端点的数的平均数.
实际数据
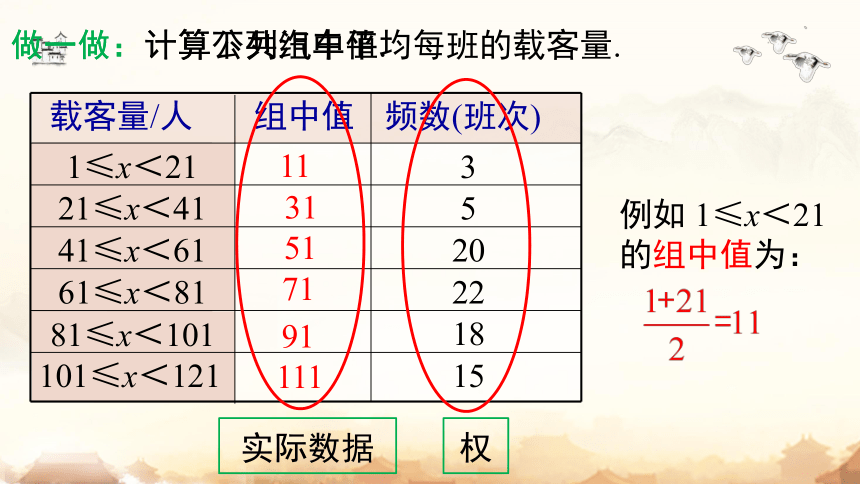
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
权
做一做:计算公共汽车平均每班的载客量.
做一做:计算下列组中值.
实际数据
例如 1≤x<21的组中值为:
解:这天 5 路公共汽车平均每班的载客量是
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器说明:
练一练
分 数 段 组中值 人 数
40≤x<60 2
60≤x<80 8
80≤x<100 10
100≤x≤120 20
问班级平均分约是多少?
某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
知识点2: 用样本平均数估计总体平均数
某灯泡厂为测量一批灯泡的使用寿命,用全面调查的方法考察这批灯泡的平均寿命,合适吗?
考察的对象很多
对考察对象带有破坏性
探究
样本估计总体
实际生活中经常用样本的平均数来估计总体的平均数.
例1 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了 50 只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
分析:
抽出 50 只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
典例精析
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是
1 672 h.
练一练
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
2.种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,
请估计这个新品种黄瓜
平均每株结多少根黄瓜.
10
15
20
18
答:估计这个新品种黄瓜平均每株约结 13 根黄瓜.
解:
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
10
15
20
18
第肆章节
随堂练习
随堂练习
知识点1:在一列数据中求加权平均数
1. 某博物馆拟招聘一名优秀讲解员,其中小华笔试、试讲、面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分为( B ).
A. 92分 B. 92.4分 C. 90分 D. 94分
B
2. 某学校生物兴趣小组共11人到校外采集植物标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个兴趣小组平均每人采集标本 件.
3. 据资料记载,位于意大利的比萨斜塔在1918—1958年这41年间,平均每年倾斜1.1 mm;在1959—1969年这11年间,平均每年倾斜1.26 mm.那么在1918—1969年这52年间,平均每年倾斜 mm.(结果保留两位小数)
4
1.13
知识点2:在统计表中求加权平均数
4. 体育课上进行了一次定点投篮比赛,每人投5次,情况如下表,若平均投中次数为2,则x等于 .
投中次数 0 1 2 3 4
学生人数 3 5 6 x 2
7
5. 某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
员工 笔试 面试 体能
甲 85 80 75
乙 80 90 73
丙 83 79 90
该公司规定:笔试、面试、体能得分分别不得低于80分,80分,70分,并按6∶3∶1的比例计入总分(不计其他因素条件),请你说明谁将被录用.
解:甲将被录用.理由如下:由题意,得丙不符合要求.
甲的成绩为85× +80× +75× =82.5(分),
乙的成绩为80× +90× +73× =82.3(分).
∵82.5>82.3,∴甲将被录用.
知识点3:在统计图中求加权平均数
6. 为调查居民生活环境质量,环保局对所辖的50个居民区进行了噪音(单位:dB)水平的调查,结果如图,则每个小区噪声的平均值是 .
65.4 dB
(第6题)
(第7题)
7. 某班40名学生的身高情况如图,则该班学生的平均身高是 .
165.5 cm
8. 某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是 分.
93
9. 某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表,求该公司每人所创年利润的平均数.
部门 A B C D E F G
人数 1 1 2 4 2 2 3
每人创得利润/万元 20 5 2.5 2.1 1.5 1.5 1.2
3.2万元.
第伍章节
课堂小结
课堂小结
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第二十章 数据的分析
汇报人:孙老师
汇报班级:X级X班
20.1.1 第2课时 用样本平均数估计总体平均数
20.1 数据的集中趋势
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解加权平均数的概念.
2.会计算加权平均数并体会权的重要性.
3.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.
第贰章节
新课导入
新课导入
简单随机抽样:
一般地,设一个总体含有N (N为正整数)个个体,从中逐个抽取n (1
抽签法 ①编号; ②制签、抽签; ③得样本. 简单易行 总体较大时操作麻烦,效果不好.
随机数法 ①编号; ②产生随机数; ③得样本. 简单易行 总体特别大时,不方便.
第叁章节
新知探究
新知探究
知识点1: 组中值与平均数
问题1:为了解 5 路公共汽车的运营情况,公交部门统计了某天 5 路公共汽车每个运行班次的载客量,得到下表,这天 5 路公共汽车平均每班的载客量是多少?
载客量/人 频数(班次)
1≤x<21 3
21 ≤x<41 5
41 ≤x<61 20
61 ≤x<81 22
81 ≤x<101 18
101 ≤x<121 15
载客量/人 频数(班次)
1≤x<21 3
21 ≤x<41 5
41 ≤x<61 20
61 ≤x<81 22
81 ≤x<101 18
101 ≤x<121 15
想一想:没有具体的数据怎么算公共汽车平均每班的载客量呢?
分析:在每组中找一个数,然后把组中的每个数都近似看做它.
组中值
近似数
组中值:这个小组的两个端点的数的平均数.
实际数据
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
权
做一做:计算公共汽车平均每班的载客量.
做一做:计算下列组中值.
实际数据
例如 1≤x<21的组中值为:
解:这天 5 路公共汽车平均每班的载客量是
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器说明:
练一练
分 数 段 组中值 人 数
40≤x<60 2
60≤x<80 8
80≤x<100 10
100≤x≤120 20
问班级平均分约是多少?
某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
知识点2: 用样本平均数估计总体平均数
某灯泡厂为测量一批灯泡的使用寿命,用全面调查的方法考察这批灯泡的平均寿命,合适吗?
考察的对象很多
对考察对象带有破坏性
探究
样本估计总体
实际生活中经常用样本的平均数来估计总体的平均数.
例1 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了 50 只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
分析:
抽出 50 只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
典例精析
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是
1 672 h.
练一练
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
2.种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,
请估计这个新品种黄瓜
平均每株结多少根黄瓜.
10
15
20
18
答:估计这个新品种黄瓜平均每株约结 13 根黄瓜.
解:
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
10
15
20
18
第肆章节
随堂练习
随堂练习
知识点1:在一列数据中求加权平均数
1. 某博物馆拟招聘一名优秀讲解员,其中小华笔试、试讲、面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分为( B ).
A. 92分 B. 92.4分 C. 90分 D. 94分
B
2. 某学校生物兴趣小组共11人到校外采集植物标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个兴趣小组平均每人采集标本 件.
3. 据资料记载,位于意大利的比萨斜塔在1918—1958年这41年间,平均每年倾斜1.1 mm;在1959—1969年这11年间,平均每年倾斜1.26 mm.那么在1918—1969年这52年间,平均每年倾斜 mm.(结果保留两位小数)
4
1.13
知识点2:在统计表中求加权平均数
4. 体育课上进行了一次定点投篮比赛,每人投5次,情况如下表,若平均投中次数为2,则x等于 .
投中次数 0 1 2 3 4
学生人数 3 5 6 x 2
7
5. 某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
员工 笔试 面试 体能
甲 85 80 75
乙 80 90 73
丙 83 79 90
该公司规定:笔试、面试、体能得分分别不得低于80分,80分,70分,并按6∶3∶1的比例计入总分(不计其他因素条件),请你说明谁将被录用.
解:甲将被录用.理由如下:由题意,得丙不符合要求.
甲的成绩为85× +80× +75× =82.5(分),
乙的成绩为80× +90× +73× =82.3(分).
∵82.5>82.3,∴甲将被录用.
知识点3:在统计图中求加权平均数
6. 为调查居民生活环境质量,环保局对所辖的50个居民区进行了噪音(单位:dB)水平的调查,结果如图,则每个小区噪声的平均值是 .
65.4 dB
(第6题)
(第7题)
7. 某班40名学生的身高情况如图,则该班学生的平均身高是 .
165.5 cm
8. 某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是 分.
93
9. 某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表,求该公司每人所创年利润的平均数.
部门 A B C D E F G
人数 1 1 2 4 2 2 3
每人创得利润/万元 20 5 2.5 2.1 1.5 1.5 1.2
3.2万元.
第伍章节
课堂小结
课堂小结
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
