14.3角的平分线(课时1)(共31张PPT)-初中数学人教版(2024)八年级上册
文档属性
| 名称 | 14.3角的平分线(课时1)(共31张PPT)-初中数学人教版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 14:44:44 | ||
图片预览




文档简介
(共31张PPT)
14.3角的平分线(课时1)
第十四章 全等三角形
人教版(2024)
素养目标
2.探索并证明角的平分线的性质定理,并能运用这个定理解决相关问题.
重点
1.能用尺规作图:作一个角的平分线,强化学生的分析与作图能力;
重点
新知导入
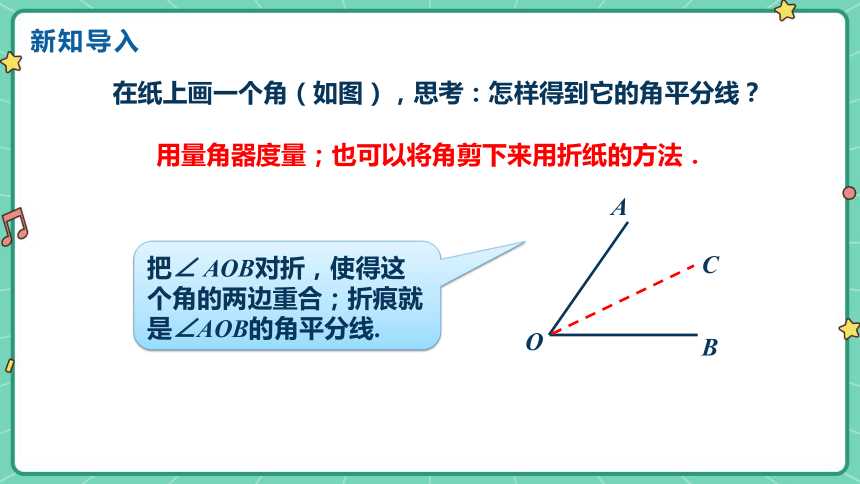
在纸上画一个角(如图),思考:怎样得到它的角平分线?
A
O
B
用量角器度量;也可以将角剪下来用折纸的方法.
C
把∠ AOB对折,使得这个角的两边重合;折痕就是∠AOB的角平分线.
探究新知
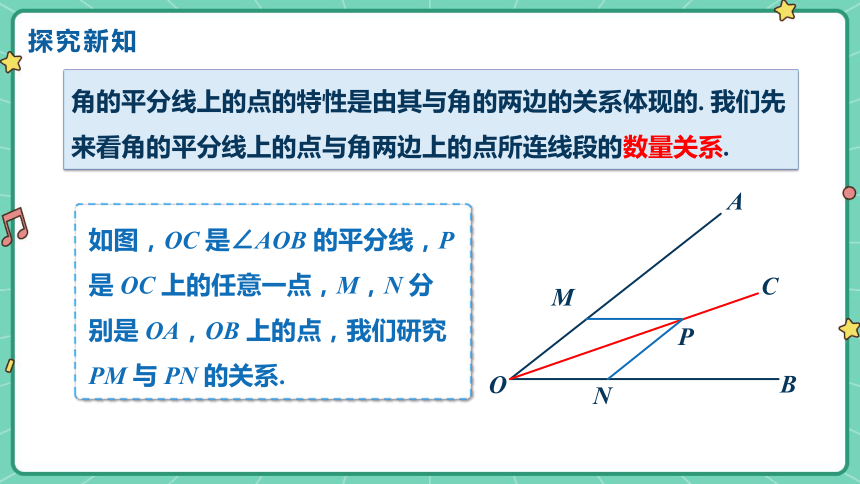
角的平分线上的点的特性是由其与角的两边的关系体现的. 我们先来看角的平分线上的点与角两边上的点所连线段的数量关系.
C
A
B
O
M
N
P
如图,OC 是∠AOB 的平分线,P 是 OC 上的任意一点,M,N 分别是 OA,OB 上的点,我们研究 PM 与 PN 的关系.
探究新知
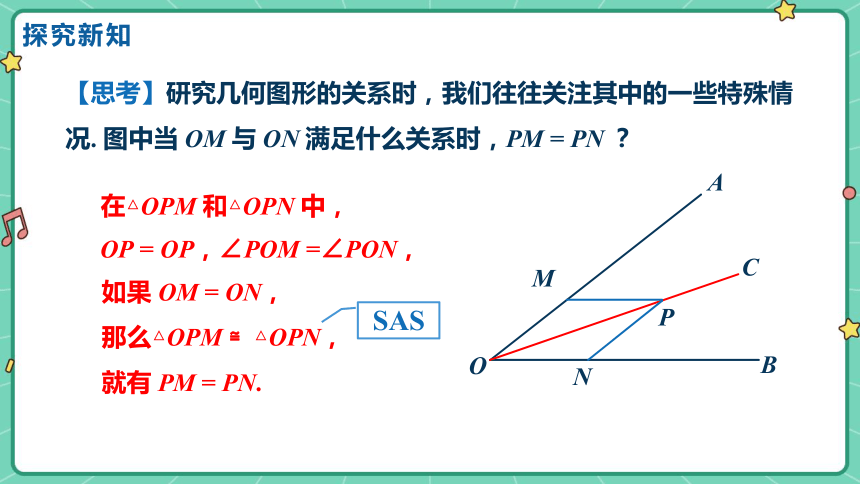
【思考】研究几何图形的关系时,我们往往关注其中的一些特殊情况. 图中当 OM 与 ON 满足什么关系时,PM = PN ?
C
A
B
O
M
N
P
OP = OP,∠POM =∠PON,
在△OPM 和△OPN 中,
如果 OM = ON,
那么△OPM ≌△OPN,
就有 PM = PN.
SAS
探究新知
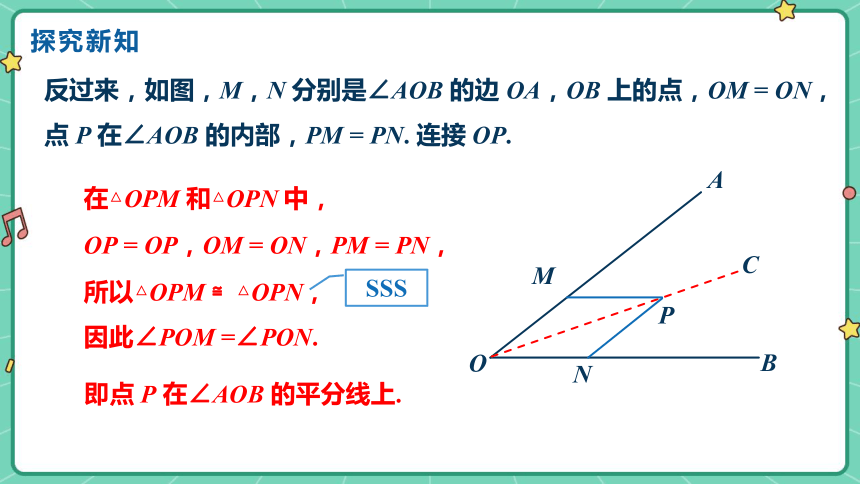
反过来,如图,M,N 分别是∠AOB 的边 OA,OB 上的点,OM = ON,点 P 在∠AOB 的内部,PM = PN. 连接 OP.
C
A
B
O
M
N
P
OP = OP,OM = ON,PM = PN,
在△OPM 和△OPN 中,
所以△OPM ≌△OPN,
因此∠POM =∠PON.
即点 P 在∠AOB 的平分线上.
SSS
探究新知
【思考】由上述结论,你能想到如何作一个角的平分线吗?
根据上述结论,可以先在角的两边上分别作出与角的顶点距离相等的两点;
再在角的内部作出与这两点距离相等的点;
以角的顶点为端点,作过这个点的射线,就能得到角的平分线了.
A
B
O
探究新知
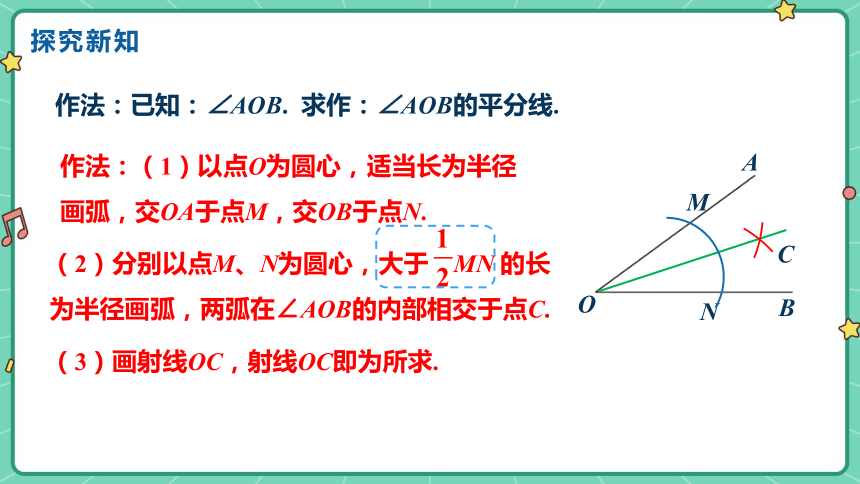
作法:已知:∠AOB. 求作:∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(3)画射线OC,射线OC即为所求.
(2)分别以点M、N为圆心,大于 MN 的长为半径画弧,两弧在∠AOB的内部相交于点C.
M
N
C
探究新知
A
B
O
M
N
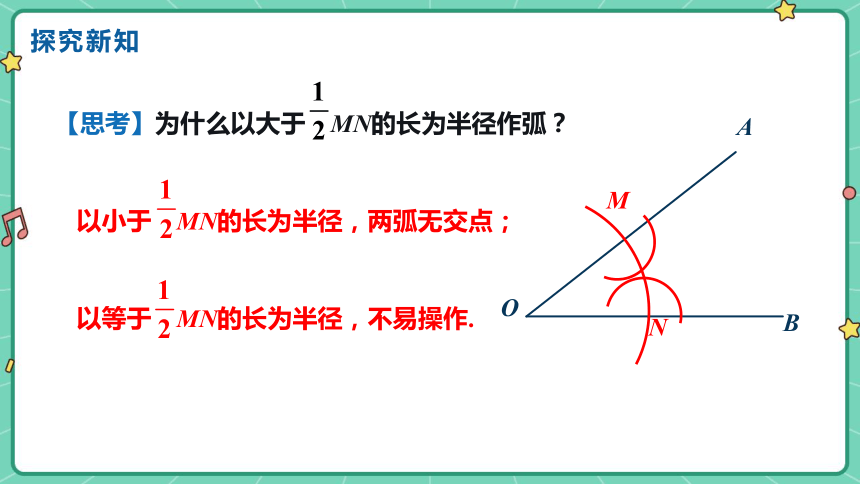
以小于 MN的长为半径,两弧无交点;
以等于 MN的长为半径,不易操作.
【思考】为什么以大于 MN的长为半径作弧?
探究新知
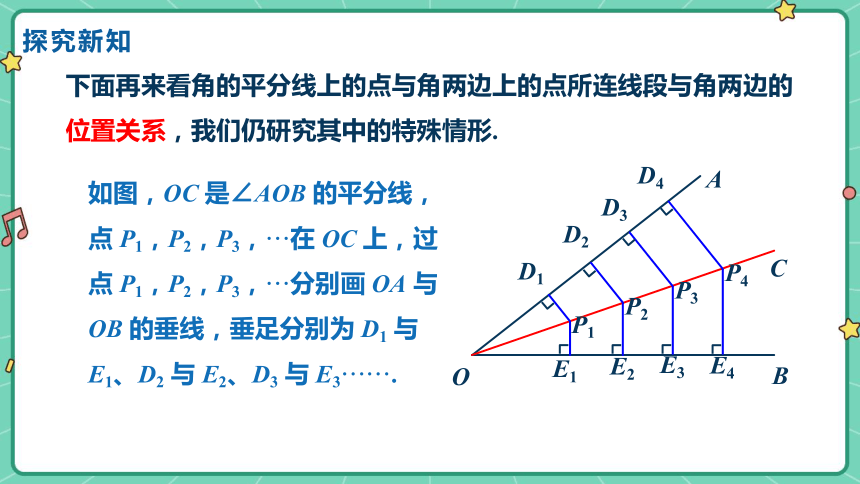
下面再来看角的平分线上的点与角两边上的点所连线段与角两边的位置关系,我们仍研究其中的特殊情形.
如图,OC 是∠AOB 的平分线,点 P1,P2,P3,···在 OC 上,过点 P1,P2,P3,···分别画 OA 与 OB 的垂线,垂足分别为 D1 与 E1、D2 与 E2、D3 与 E3······.
C
A
B
O
D1
E1
P1
D2
E2
P2
D3
E3
P3
D4
E4
P4
探究新知
C
A
B
O
D1
E1
P1
D2
E2
P2
D3
E3
P3
D4
E4
P4
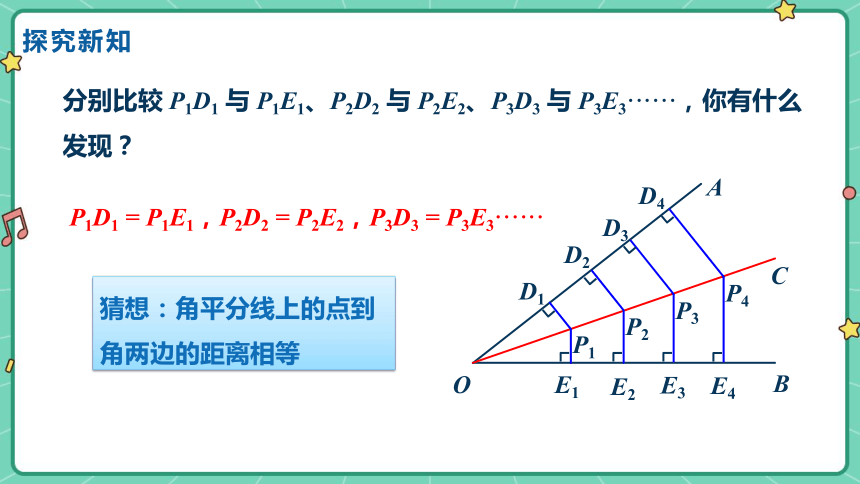
分别比较 P1D1 与 P1E1、P2D2 与 P2E2、P3D3 与 P3E3······,你有什么发现?
P1D1 = P1E1,P2D2 = P2E2,P3D3 = P3E3······
猜想:角平分线上的点到角两边的距离相等
探究新知
证明
已知:
一个点在一个角的平分线上.
求证:
这个点到这个角两边的距离相等.
为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.
探究新知
如图,OC 是∠AOB 的平分线,点 P 在 OC 上,PD⊥OA,PE⊥OB,垂足分别为 D,E.
求证 PD = PE.
C
A
B
O
D
E
P
【分析】证明△OPD≌△OPE
PD = PE
探究新知
C
A
B
O
D
E
P
证明:∵OC 是∠AOB 的平分线,∴∠AOC =∠BOC.
∵PD⊥OA,PE⊥OB,∴ ∠PDO =∠PEO = 90°.
在△OPD 和△OPE 中,
∠AOC = ∠BOC ,
∠PDO = ∠PEO ,
OP = OP ,
∴ △OPD ≌ △OPE(AAS)
∴PD = PE
归纳总结
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
符号语言:
∵OC 是∠AOB的平分线,P是OC上的一点,
∴PD = PE
PD⊥OA,PE⊥OB,垂足分别是D、E
P
A
O
B
C
D
E
归纳总结
证明一个几何命题时的步骤:
已知:一个点在一个角的平分线上
求证:这个点到角两边的距离相等;
第一步:明确命题中的已知和求证
第二步:根据已知和求证,画出图形,并用数学符号表示已知和求证;
第三步:经过分析,找出由已知推出要证的结论的途径,写出证明过程.
C
B
6
2
D
C
D
小结
角的平分线
(课时1)
尺规作图
性质
作一个角的平分线,依据:SSS
角的平分线上的点到角的两边的距离相等
谢谢同学们的聆听
14.3角的平分线(课时1)
第十四章 全等三角形
人教版(2024)
素养目标
2.探索并证明角的平分线的性质定理,并能运用这个定理解决相关问题.
重点
1.能用尺规作图:作一个角的平分线,强化学生的分析与作图能力;
重点
新知导入
在纸上画一个角(如图),思考:怎样得到它的角平分线?
A
O
B
用量角器度量;也可以将角剪下来用折纸的方法.
C
把∠ AOB对折,使得这个角的两边重合;折痕就是∠AOB的角平分线.
探究新知
角的平分线上的点的特性是由其与角的两边的关系体现的. 我们先来看角的平分线上的点与角两边上的点所连线段的数量关系.
C
A
B
O
M
N
P
如图,OC 是∠AOB 的平分线,P 是 OC 上的任意一点,M,N 分别是 OA,OB 上的点,我们研究 PM 与 PN 的关系.
探究新知
【思考】研究几何图形的关系时,我们往往关注其中的一些特殊情况. 图中当 OM 与 ON 满足什么关系时,PM = PN ?
C
A
B
O
M
N
P
OP = OP,∠POM =∠PON,
在△OPM 和△OPN 中,
如果 OM = ON,
那么△OPM ≌△OPN,
就有 PM = PN.
SAS
探究新知
反过来,如图,M,N 分别是∠AOB 的边 OA,OB 上的点,OM = ON,点 P 在∠AOB 的内部,PM = PN. 连接 OP.
C
A
B
O
M
N
P
OP = OP,OM = ON,PM = PN,
在△OPM 和△OPN 中,
所以△OPM ≌△OPN,
因此∠POM =∠PON.
即点 P 在∠AOB 的平分线上.
SSS
探究新知
【思考】由上述结论,你能想到如何作一个角的平分线吗?
根据上述结论,可以先在角的两边上分别作出与角的顶点距离相等的两点;
再在角的内部作出与这两点距离相等的点;
以角的顶点为端点,作过这个点的射线,就能得到角的平分线了.
A
B
O
探究新知
作法:已知:∠AOB. 求作:∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(3)画射线OC,射线OC即为所求.
(2)分别以点M、N为圆心,大于 MN 的长为半径画弧,两弧在∠AOB的内部相交于点C.
M
N
C
探究新知
A
B
O
M
N
以小于 MN的长为半径,两弧无交点;
以等于 MN的长为半径,不易操作.
【思考】为什么以大于 MN的长为半径作弧?
探究新知
下面再来看角的平分线上的点与角两边上的点所连线段与角两边的位置关系,我们仍研究其中的特殊情形.
如图,OC 是∠AOB 的平分线,点 P1,P2,P3,···在 OC 上,过点 P1,P2,P3,···分别画 OA 与 OB 的垂线,垂足分别为 D1 与 E1、D2 与 E2、D3 与 E3······.
C
A
B
O
D1
E1
P1
D2
E2
P2
D3
E3
P3
D4
E4
P4
探究新知
C
A
B
O
D1
E1
P1
D2
E2
P2
D3
E3
P3
D4
E4
P4
分别比较 P1D1 与 P1E1、P2D2 与 P2E2、P3D3 与 P3E3······,你有什么发现?
P1D1 = P1E1,P2D2 = P2E2,P3D3 = P3E3······
猜想:角平分线上的点到角两边的距离相等
探究新知
证明
已知:
一个点在一个角的平分线上.
求证:
这个点到这个角两边的距离相等.
为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.
探究新知
如图,OC 是∠AOB 的平分线,点 P 在 OC 上,PD⊥OA,PE⊥OB,垂足分别为 D,E.
求证 PD = PE.
C
A
B
O
D
E
P
【分析】证明△OPD≌△OPE
PD = PE
探究新知
C
A
B
O
D
E
P
证明:∵OC 是∠AOB 的平分线,∴∠AOC =∠BOC.
∵PD⊥OA,PE⊥OB,∴ ∠PDO =∠PEO = 90°.
在△OPD 和△OPE 中,
∠AOC = ∠BOC ,
∠PDO = ∠PEO ,
OP = OP ,
∴ △OPD ≌ △OPE(AAS)
∴PD = PE
归纳总结
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
符号语言:
∵OC 是∠AOB的平分线,P是OC上的一点,
∴PD = PE
PD⊥OA,PE⊥OB,垂足分别是D、E
P
A
O
B
C
D
E
归纳总结
证明一个几何命题时的步骤:
已知:一个点在一个角的平分线上
求证:这个点到角两边的距离相等;
第一步:明确命题中的已知和求证
第二步:根据已知和求证,画出图形,并用数学符号表示已知和求证;
第三步:经过分析,找出由已知推出要证的结论的途径,写出证明过程.
C
B
6
2
D
C
D
小结
角的平分线
(课时1)
尺规作图
性质
作一个角的平分线,依据:SSS
角的平分线上的点到角的两边的距离相等
谢谢同学们的聆听
同课章节目录
