14.3角的平分线(课时2)(共22张PPT)-初中数学人教版(2024)八年级上册
文档属性
| 名称 | 14.3角的平分线(课时2)(共22张PPT)-初中数学人教版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 14:45:17 | ||
图片预览




文档简介
(共22张PPT)
14.3角的平分线(课时2)
第十四章 全等三角形
人教版(2024)
素养目标
2.能够运用角的平分线的判定定理解决相关问题.
重点
1.探索并证明角的平分线的判定定理,感受互逆的数学思想,发展学生的推理能力和解题能力;
重点
复习导入
角的平分线的性质: .
角的平分线上的点到角的两边的距离相等
反过来,交换这个性质的题设和结论,得到的命题还成立吗?也就是说,到角两边距离相等的点一定在角的平分线上吗?
探究新知
已知:
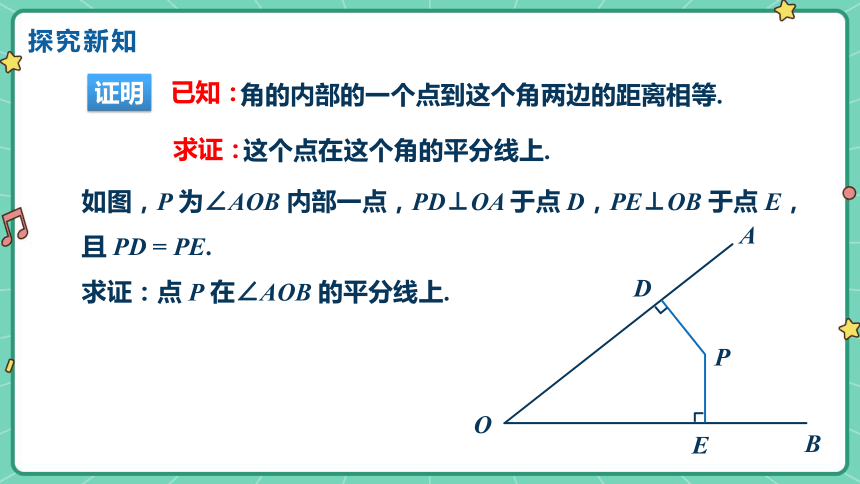
角的内部的一个点到这个角两边的距离相等.
求证:
这个点在这个角的平分线上.
证明
如图,P 为∠AOB 内部一点,PD⊥OA 于点 D,PE⊥OB 于点 E,且 PD = PE.
求证:点 P 在∠AOB 的平分线上.
A
B
O
D
E
P
探究新知
C
A
B
O
D
E
P
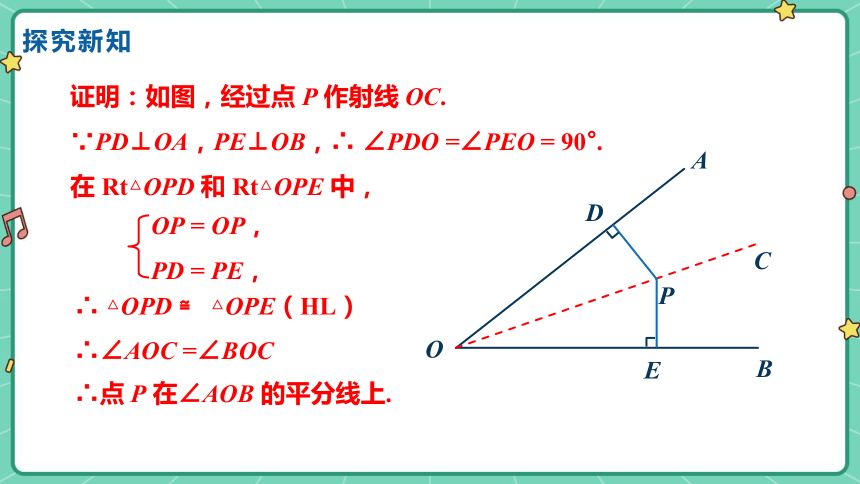
证明:如图,经过点 P 作射线 OC.
∵PD⊥OA,PE⊥OB,∴ ∠PDO =∠PEO = 90°.
在 Rt△OPD 和 Rt△OPE 中,
OP = OP,
PD = PE,
∴ △OPD ≌ △OPE(HL)
∴∠AOC =∠BOC
∴点 P 在∠AOB 的平分线上.
归纳总结
角的平分线的判定定理:
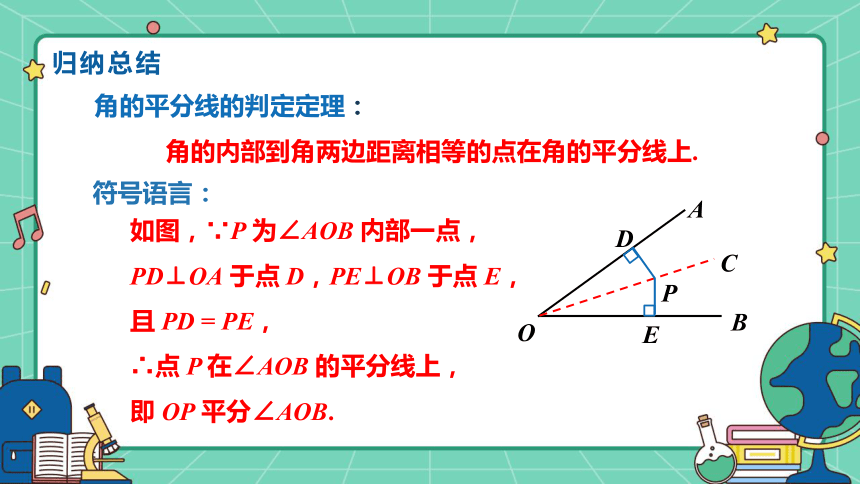
角的内部到角两边距离相等的点在角的平分线上.
符号语言:
如图,∵P 为∠AOB 内部一点,PD⊥OA 于点 D,PE⊥OB 于点 E,
且 PD = PE,
∴点 P 在∠AOB 的平分线上,
即 OP 平分∠AOB.
P
A
O
B
C
D
E
归纳总结
从上面两个结论可以看出,角的平分线上的点到角两边的距离相等;
反过来,角的内部到角两边距离相等的点在角的平分线上.
所以在角的内部,角的平分线(顶点除外)可以看成到角两边距离相等的所有点的集合.
所有到角两边距离相等的点组成这个角的平分线.
例题练习
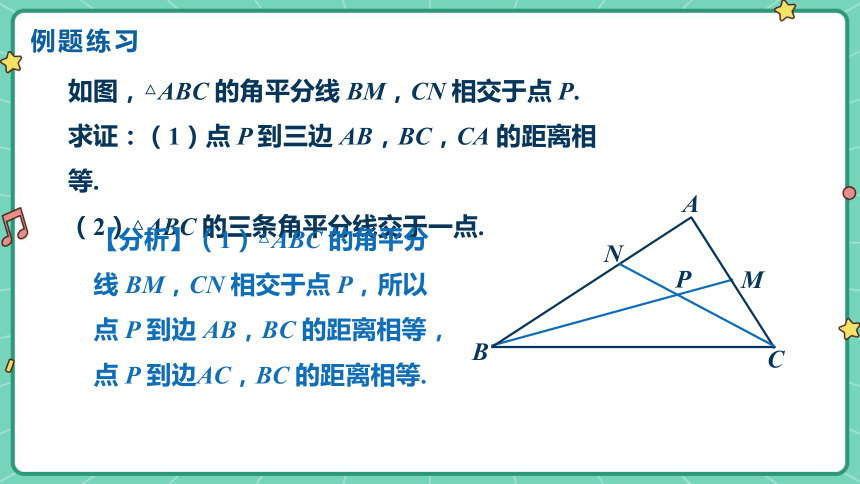
如图,△ABC 的角平分线 BM,CN 相交于点 P.
求证:(1)点 P 到三边 AB,BC,CA 的距离相等.
(2)△ABC 的三条角平分线交于一点.
A
B
C
P
N
M
【分析】(1)△ABC 的角平分线 BM,CN 相交于点 P,所以点 P 到边 AB,BC 的距离相等,点 P 到边AC,BC 的距离相等.
例题练习
D
E
F
A
B
C
P
N
M
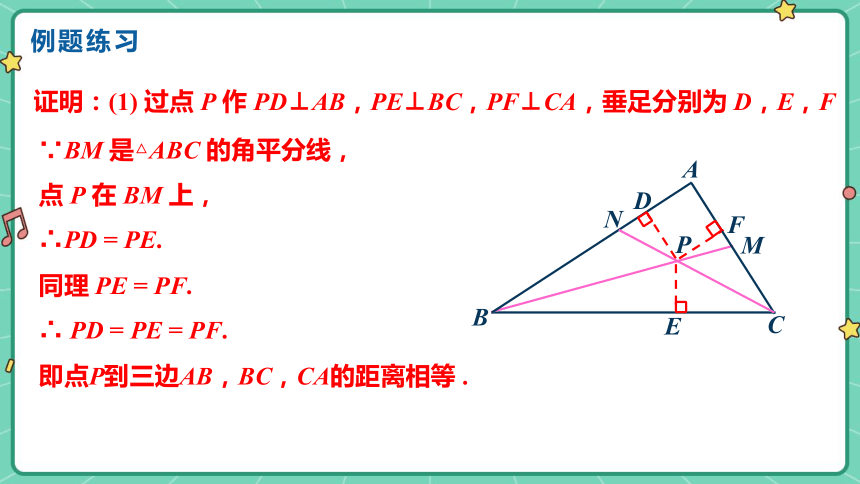
证明:(1) 过点 P 作 PD⊥AB,PE⊥BC,PF⊥CA,垂足分别为 D,E,F
∵BM 是△ABC 的角平分线,
点 P 在 BM 上,
∴PD = PE.
同理 PE = PF.
∴ PD = PE = PF.
即点P到三边AB,BC,CA的距离相等 .
例题练习
如图,△ABC 的角平分线 BM,CN 相交于点 P.
求证:(1)点 P 到三边 AB,BC,CA 的距离相等.
(2)△ABC 的三条角平分线交于一点.
【分析】(2)要证△ABC 的三条角平分线交于一点,只要证点 P 也在∠A 的平分线上.
(2)由 (1) 得,点 P 到边 AB,CA 的距离相等,
∴点 P 在∠A 的平分线上 .
∴△ABC 的三条角平分线交于一点 .
A
B
C
P
N
M
C
C
D
小结
角平分线的判定
内容
作用
角的内部到角两边距离相等的点在角的平分线上
判断一个点是否在角的平分线上
谢谢同学们的聆听
14.3角的平分线(课时2)
第十四章 全等三角形
人教版(2024)
素养目标
2.能够运用角的平分线的判定定理解决相关问题.
重点
1.探索并证明角的平分线的判定定理,感受互逆的数学思想,发展学生的推理能力和解题能力;
重点
复习导入
角的平分线的性质: .
角的平分线上的点到角的两边的距离相等
反过来,交换这个性质的题设和结论,得到的命题还成立吗?也就是说,到角两边距离相等的点一定在角的平分线上吗?
探究新知
已知:
角的内部的一个点到这个角两边的距离相等.
求证:
这个点在这个角的平分线上.
证明
如图,P 为∠AOB 内部一点,PD⊥OA 于点 D,PE⊥OB 于点 E,且 PD = PE.
求证:点 P 在∠AOB 的平分线上.
A
B
O
D
E
P
探究新知
C
A
B
O
D
E
P
证明:如图,经过点 P 作射线 OC.
∵PD⊥OA,PE⊥OB,∴ ∠PDO =∠PEO = 90°.
在 Rt△OPD 和 Rt△OPE 中,
OP = OP,
PD = PE,
∴ △OPD ≌ △OPE(HL)
∴∠AOC =∠BOC
∴点 P 在∠AOB 的平分线上.
归纳总结
角的平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上.
符号语言:
如图,∵P 为∠AOB 内部一点,PD⊥OA 于点 D,PE⊥OB 于点 E,
且 PD = PE,
∴点 P 在∠AOB 的平分线上,
即 OP 平分∠AOB.
P
A
O
B
C
D
E
归纳总结
从上面两个结论可以看出,角的平分线上的点到角两边的距离相等;
反过来,角的内部到角两边距离相等的点在角的平分线上.
所以在角的内部,角的平分线(顶点除外)可以看成到角两边距离相等的所有点的集合.
所有到角两边距离相等的点组成这个角的平分线.
例题练习
如图,△ABC 的角平分线 BM,CN 相交于点 P.
求证:(1)点 P 到三边 AB,BC,CA 的距离相等.
(2)△ABC 的三条角平分线交于一点.
A
B
C
P
N
M
【分析】(1)△ABC 的角平分线 BM,CN 相交于点 P,所以点 P 到边 AB,BC 的距离相等,点 P 到边AC,BC 的距离相等.
例题练习
D
E
F
A
B
C
P
N
M
证明:(1) 过点 P 作 PD⊥AB,PE⊥BC,PF⊥CA,垂足分别为 D,E,F
∵BM 是△ABC 的角平分线,
点 P 在 BM 上,
∴PD = PE.
同理 PE = PF.
∴ PD = PE = PF.
即点P到三边AB,BC,CA的距离相等 .
例题练习
如图,△ABC 的角平分线 BM,CN 相交于点 P.
求证:(1)点 P 到三边 AB,BC,CA 的距离相等.
(2)△ABC 的三条角平分线交于一点.
【分析】(2)要证△ABC 的三条角平分线交于一点,只要证点 P 也在∠A 的平分线上.
(2)由 (1) 得,点 P 到边 AB,CA 的距离相等,
∴点 P 在∠A 的平分线上 .
∴△ABC 的三条角平分线交于一点 .
A
B
C
P
N
M
C
C
D
小结
角平分线的判定
内容
作用
角的内部到角两边距离相等的点在角的平分线上
判断一个点是否在角的平分线上
谢谢同学们的聆听
同课章节目录
