(核心素养应用意识)第七单元折线统计图(解决问一)(含解析)-五年级数学下册人教版
文档属性
| 名称 | (核心素养应用意识)第七单元折线统计图(解决问一)(含解析)-五年级数学下册人教版 |  | |
| 格式 | doc | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 04:51:12 | ||
图片预览

文档简介
/ 让教学更有效 精品试卷 | 数学学科
(核心素养应用意识)第七单元折线统计图(解决问一)-五年级数学下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、解答题
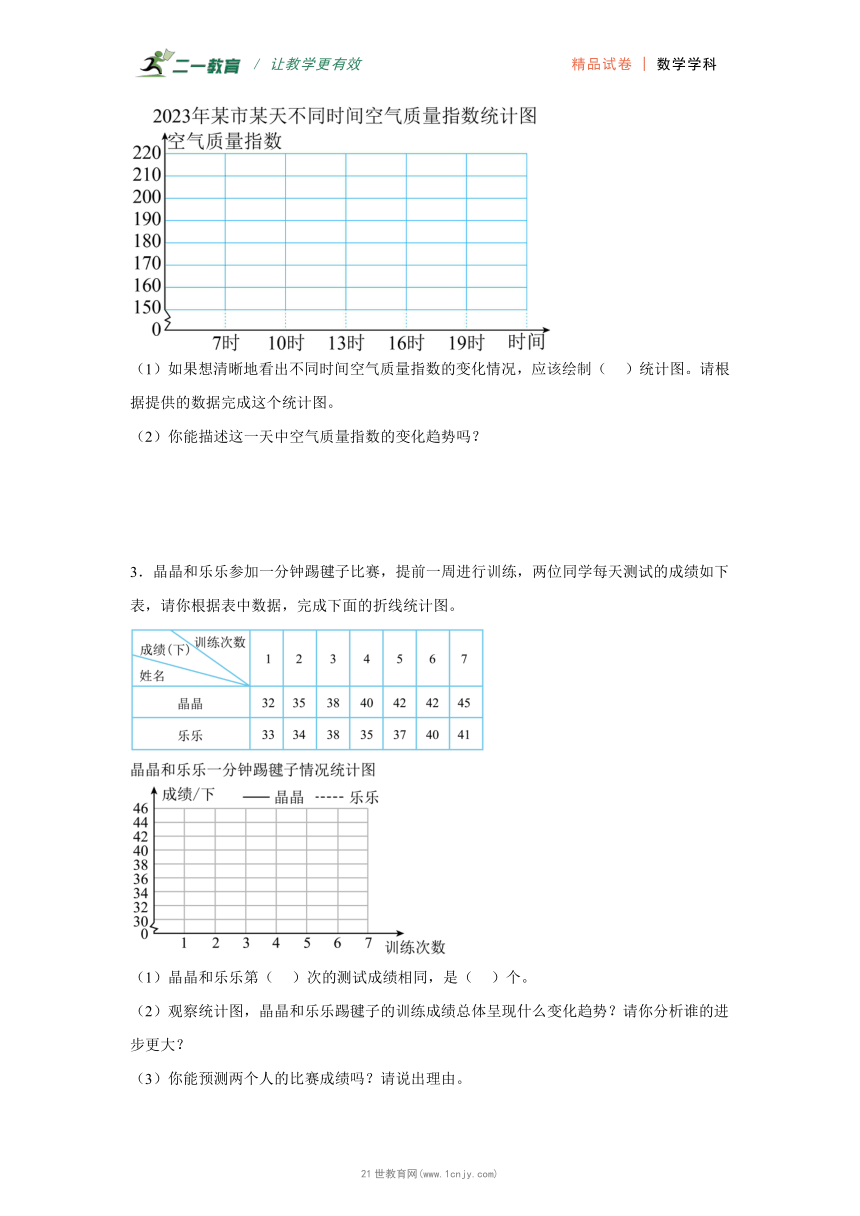
1.如图所示是某家电商场A、B两种品牌电视机2021年月销售量统计图。观察这个折线统计图所呈现的数据,回答下面的问题。
(1)折线统计图适合呈现数据的( )情况。
(2)如果你是商场的经理,你能从上面的复式折线统计图中得到哪些信息?这些信息对你有什么帮助?
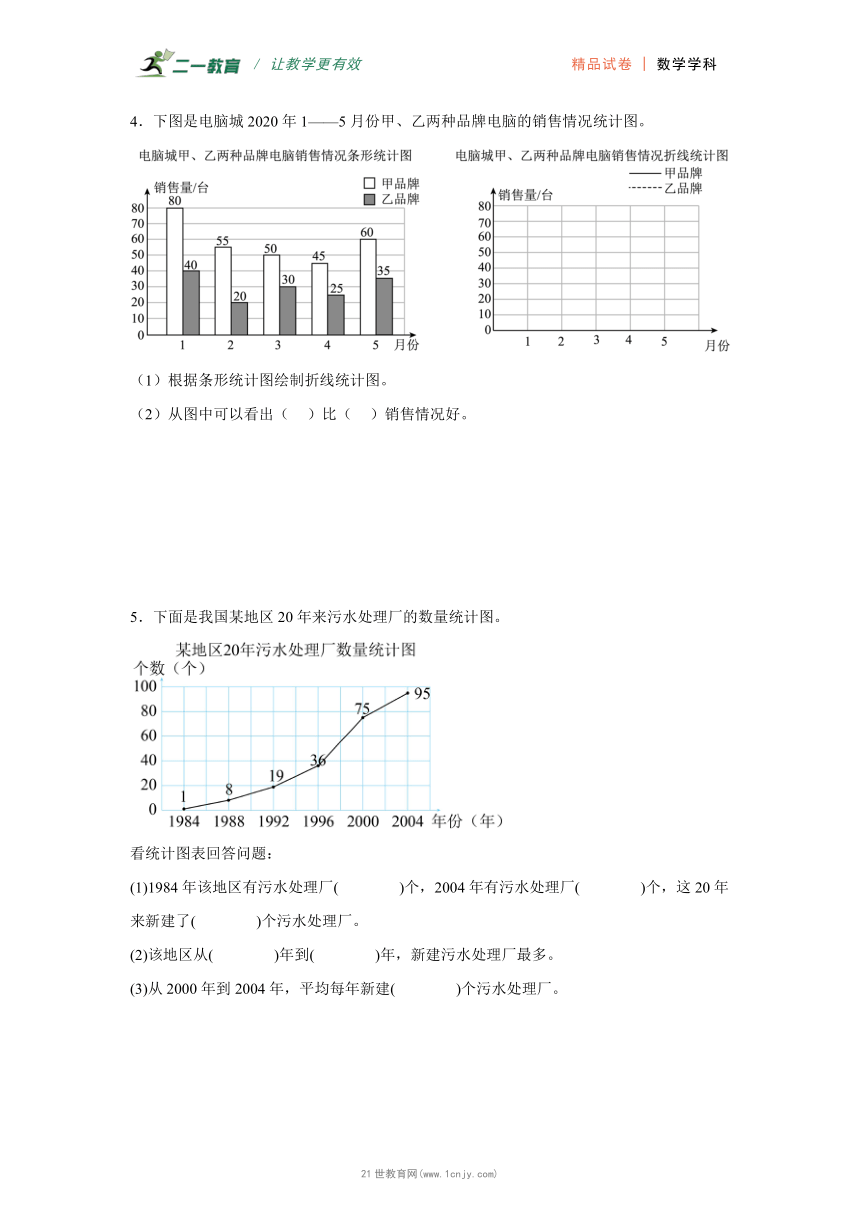
2.下面是2023年某市某天不同时间空气质量指数统计表。
时间 7时 10时 13时 16时 19时
空气质量指数 155 198 210 195 180
(1)如果想清晰地看出不同时间空气质量指数的变化情况,应该绘制( )统计图。请根据提供的数据完成这个统计图。
(2)你能描述这一天中空气质量指数的变化趋势吗?
3.晶晶和乐乐参加一分钟踢毽子比赛,提前一周进行训练,两位同学每天测试的成绩如下表,请你根据表中数据,完成下面的折线统计图。
(1)晶晶和乐乐第( )次的测试成绩相同,是( )个。
(2)观察统计图,晶晶和乐乐踢毽子的训练成绩总体呈现什么变化趋势?请你分析谁的进步更大?
(3)你能预测两个人的比赛成绩吗?请说出理由。
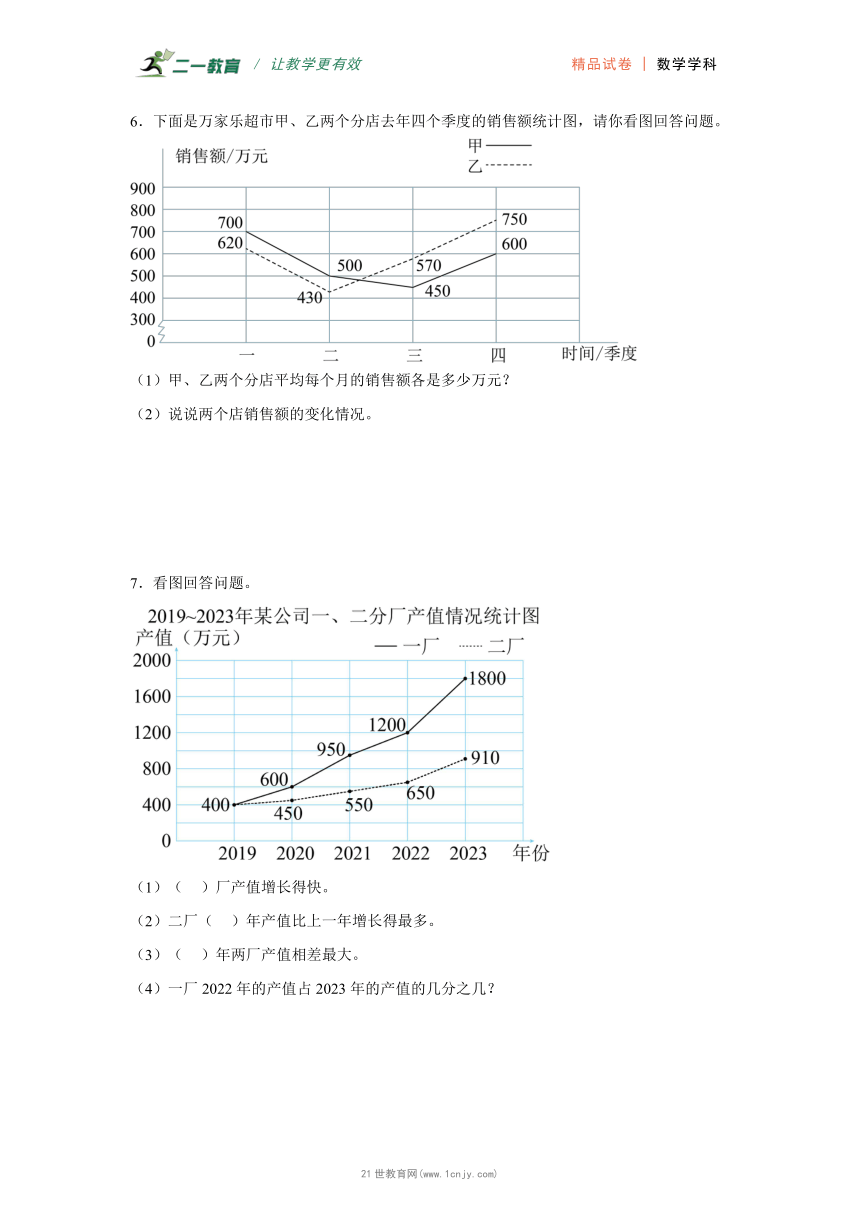
4.下图是电脑城2020年1——5月份甲、乙两种品牌电脑的销售情况统计图。
(1)根据条形统计图绘制折线统计图。
(2)从图中可以看出( )比( )销售情况好。
5.下面是我国某地区20年来污水处理厂的数量统计图。
看统计图表回答问题:
(1)1984年该地区有污水处理厂( )个,2004年有污水处理厂( )个,这20年来新建了( )个污水处理厂。
(2)该地区从( )年到( )年,新建污水处理厂最多。
(3)从2000年到2004年,平均每年新建( )个污水处理厂。
6.下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图,请你看图回答问题。
(1)甲、乙两个分店平均每个月的销售额各是多少万元?
(2)说说两个店销售额的变化情况。
7.看图回答问题。
(1)( )厂产值增长得快。
(2)二厂( )年产值比上一年增长得最多。
(3)( )年两厂产值相差最大。
(4)一厂2022年的产值占2023年的产值的几分之几?
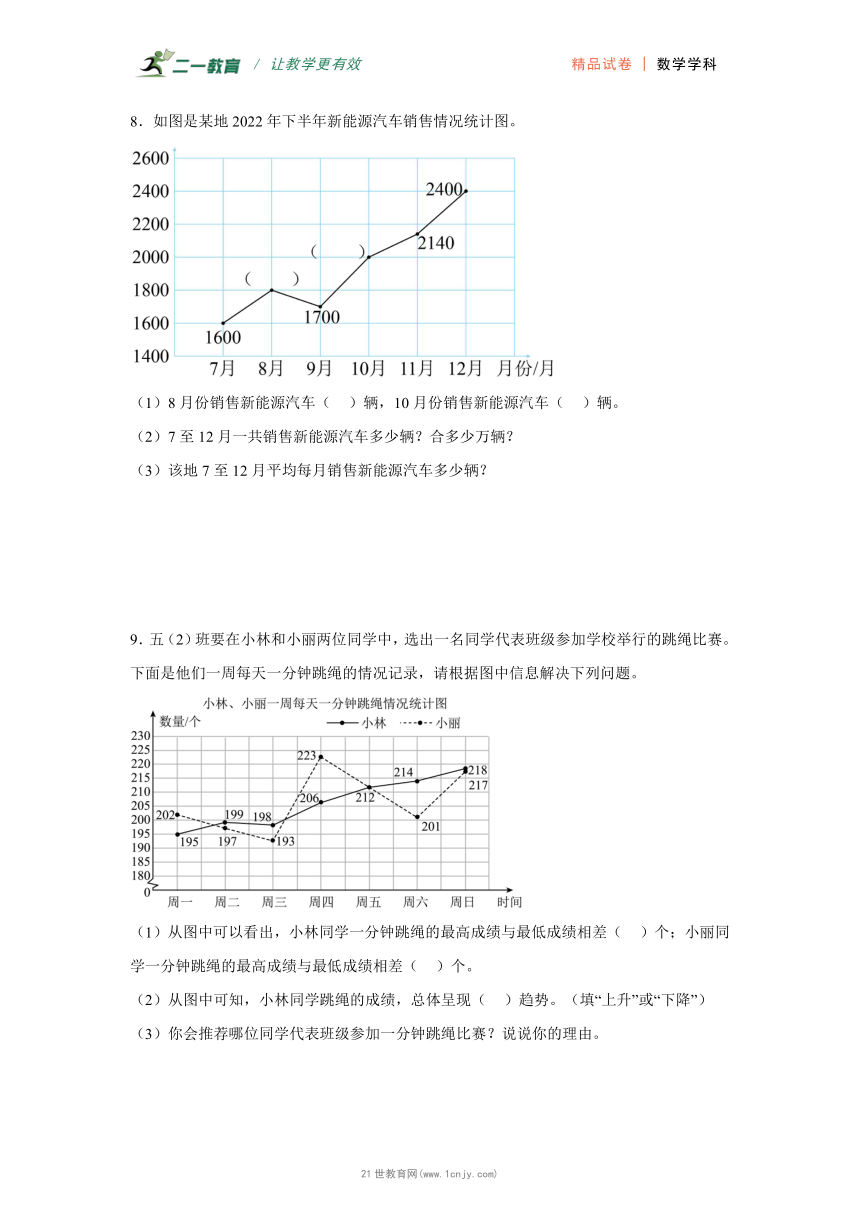
8.如图是某地2022年下半年新能源汽车销售情况统计图。
(1)8月份销售新能源汽车( )辆,10月份销售新能源汽车( )辆。
(2)7至12月一共销售新能源汽车多少辆?合多少万辆?
(3)该地7至12月平均每月销售新能源汽车多少辆?
9.五(2)班要在小林和小丽两位同学中,选出一名同学代表班级参加学校举行的跳绳比赛。下面是他们一周每天一分钟跳绳的情况记录,请根据图中信息解决下列问题。
(1)从图中可以看出,小林同学一分钟跳绳的最高成绩与最低成绩相差( )个;小丽同学一分钟跳绳的最高成绩与最低成绩相差( )个。【来源:21·世纪·教育·网】
(2)从图中可知,小林同学跳绳的成绩,总体呈现( )趋势。(填“上升”或“下降”)
(3)你会推荐哪位同学代表班级参加一分钟跳绳比赛?说说你的理由。
10.下面是小强7-12岁每年的身高与同龄男童标准身高的对比统计表。
年龄(岁)身高(厘米) 7 8 9 10 11 12
标准身高 124 130 135.4 140.2 145.3 151.9
小强身高 122.8 132 136.5 145 156.5 170
(1)根据表中数据,补充完折线统计图。
(2)与标准身高比较,同年龄低于或高于5厘米属于正常范围,小强( )岁至( )岁身高在正常范围内。www-2-1-cnjy-com
(3)小强从( )岁到( )岁身高增长最快,身高偏高。
11.学校放学时,小夏直接走路回家,行程情况统计如下图所示。到家后,小夏倒了一杯纯牛奶,先喝了整杯的,再开始做语文作业,用了小时完成;休息了一会儿,他发现牛奶凉了,就兑满了热水,又喝了半杯后,开始写数学作业,结果比完成语文作业少用了小时。然后,他就愉快地出去玩了。
(1)小夏回家途中的休息时间占路上总时间的几分之几?
(2)小夏回家做作业一共用了多少小时?
(3)在这整个过程中,小夏一共喝了多少杯纯牛奶?
12.小华了解到2018年~2023年全国燃油车和新能源车销售量情况如下图。请根据图中信息回答问题。21*cnjy*com
2018年~2023年全国燃油车和新能源车销售量情况统计图
①从上图可看出,燃油车和新能源车在2018年~2023年的销售量总体呈现怎样的趋势?
②在相邻的年份中,新能源车在相邻年份( )年至( )年的销售量上升幅度最大。
③燃油车和新能源车( )年的销售量差距最小,相差( )万辆。
13.某汽车销售店2021年至2024年销售情况如下表。
年份 2021 2022 2023 2024
数量(辆) 550 750 1500 1800
(1)根据上表的数据,把下面的折线统计图补充完整。
(2)在相邻年份中,销量增长最多的是(______年到______年)。
(3)这四年的平均销量有( )辆。
(4)整体上看,其销售情况的趋势怎样?
14.将下图中的条形统计图改画成折线统计图。
(1)你发现折线统计图有什么特点?
(2)中小学生参观科技展览的人数有什么变化?你有什么感想?
15.下面是两个服装店2023年的销售情况统计图。
(1)从图上看,( )月是销售服装的淡季。
(2)下半年,销售增长较稳定的是( )服装店。
(3)9—10月份,红星服装店的销售量比红光服装店多几分之几?
16.下面是某百货商店2022年下半年毛衣和衬衫销售情况统计图。看图说出毛衣的销售量在哪个月最大?衬衫呢?你能分析它们的销售量变化情况吗?
17.如图是一辆公交车从起始站至终点站的行驶过程中乘客上下车情况统计图。
(1)请把统计图中的图例补充完整。
(2)从图中可以看出,第( )站上车乘客和下车乘客一样多,第( )站下车乘客最多。
(3)这辆公交车最多时载( )位乘客。
18.暑假,王老师一家自驾去离家380千米的景点玩,如图是他们离家的距离与汽车行驶时间之间的关系图。
(1)王老师一家出发30分钟时,离家多少千米?
(2)出发后3小时,距离目的地多少千米?
19.下图是第25~30届奥运会上中国和美国获金牌数量的统计图。
(1)两个国家的奥运会金牌数量是逐年提高的吗?哪一届奥运会上两国金牌数量相差最少?
(2)中国和美国哪个国家金牌数量变化得较平稳?
20.某地2021年上半年每月降水量和2022年上半年每月降水量情况如下表:
降水量月份 一月 二月 三月 四月 五月 六月
2022年 19 24 51 50 32 34
2021年 10 12 25 34 38 40
(1)根据上表中的数据制成复式折线统计图。
(2)2022年四月份的降水量比2021年同期增加了( )毫米。
(3)2022年五月份的降水量是2021年同期的。
(4)2021年上半年月平均降水量比2022年上半年月平均降水量少了多少毫米?
21.如下图所示,有一个无水的长方体水槽,一个水龙头从9:00开始向水槽内注水,水流速度为9立方分米/分,9:04停止注水。接着在水槽内放入一个高为9厘米的长方体铁块,使其全部浸没在水中。从开始注水到铁块全部浸没在水中,水槽的水面高度变化情况如图中所示。21教育名师原创作品
(1)9:04时,长方体水槽内水面高度是多少厘米?
(2)这个长方体铁块的底面积是多少平方厘米?
22.下面是从同一车站发出的两辆车的运行情况。
(1)2路车与4路车在( )第二次相遇。
(2)2路车和4路车平均每小时各行多少千米?
(3)在4路车开出几小时后,两车行驶的路程相差最多?相差多少千米?
23.一辆货车从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地。已知甲乙两地的路程是330千米,货车在途中停留半小时。两车离甲地的路程与时间关系如图所示。轿车比货车早几小时到达乙地?2-1-c-n-j-y
24.甲、乙两车分别从A,B两地同时相向匀速行驶。当乙车到达地后,继续保持原速向远离的方向行驶,而甲车到达地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达地。设两车行驶的时间为(小时),两车之间的距离为(千米),与之间的关系如图所示,则B,C两地相距多少千米。
《(核心素养应用意识)第七单元折线统计图(解决问一)-五年级数学下册人教版》参考答案
1.(1)增减变化;
(2)从复式折线统计图中可以看出2021年A品牌电视机的销售量总体呈下降趋势;B品牌电视机的销售量总体比较稳定,并呈上升趋势,应少进A品牌电视机。
【分析】(1)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
(2)实线表示A品牌的销售情况,虚线表示B品牌的销售情况,通过观察两条线的走向,实线呈下降趋势,虚线呈上升趋势,但还是比较稳定。
【详解】(1)折线统计图适合呈现数据的增减变化情况。
(2)从复式折线统计图中可以看出2021年A品牌电视机的销售量总体呈下降趋势;B品牌电视机的销售量总体比较稳定,并呈上升趋势,应少进A品牌电视机。
2.(1)折线;
图见详解
(2)从7时到13时,空气质量指数逐渐上升,从13时到19时,空气质量逐渐下降(答案不唯一)
【分析】(1)根据条形统计图的特点:能够反应数据的多少;折线统计图:可以看出数据的增减变化情况,由于要反应空气质量指数的变化情况,应绘制折线统计图,先描点,再连线即可画出统计图;
(2)根据图中数据,在13时空气质量指数最高,从7时到13时逐渐上升,13时之后开始下降,说法合理即可;据此即可解答。
【详解】(1)如果想清晰地看出不同时间空气质量指数的变化情况,应该绘制折线统计图。
如图:
(2)答:从7时到13时,空气质量指数逐渐上升,从13时到19时,空气质量逐渐下降。(答案不唯一)
3.图见详解
(1)3;38
(2)见详解(答案不唯一)
(3)见详解(答案不唯一)
【分析】画图时,横轴代表测试次数,纵轴代表成绩(下),根据表格所给数据,看横轴描出纵轴的对应点,再将各点依次连接可作出统计图;
(1)两条折线的交点对应的横轴,就是测试成绩相同的次数;
(2)折线走向是上升的则成绩上升,折线走向下降则成绩下降,折线越陡成绩变化越大;
(3)根据图中折线走向、表中次数来预测二人成绩。
【详解】
(1)有图表可知:
晶晶和乐乐第3次的测试成绩相同,是38个。
(2)答:晶晶的成绩一直呈上升趋势,乐乐的成绩有下降的时候,并且晶晶的成绩大多数高于乐乐的成绩,所以,晶晶的成绩进步更大。(答案不唯一,合理即可)
(3)答:预测两个人的比赛成绩总体呈上升趋势均可能大于40下,晶晶的成绩好于乐乐的成绩,且晶晶的成绩较稳定。(答案不唯一,合理即可)www.21-cn-jy.com
4.(1)见详解;(2)甲品牌;乙品牌
【分析】(1)根据条形统计图,分别描出相应的点,再依次连接即可;用实线表示甲品牌的销售情况,用虚线表示乙品牌的销售情况。
(2)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;通过观察折线统计图的走向,实线高于虚线,所以甲品牌比乙品牌的销售情况好。
【详解】(1)如图:
(2)通过观察可知,甲品牌比乙品牌的销售情况好。
5.(1) 1 95 94
(2) 1996 2000
(3)5
【分析】(1)根据图示,1984年对应污水处理厂1个,2004年有污水处理厂95个。新建的数量就是2004年的数量减去1984年的数量,即95-1=94(个)
(2)根据图示,1984—1988年新建污水处理厂8-1=7(个);
1988年—1992年新建污水处理厂19-8=11(个);
1992—1996年新建污水处理厂36-19=17(个);
1996—2000年新建污水处理厂75-36=39(个);
2000—2004年新建污水处理厂95-75=20(个);
综上区间数据1996年—2000年新建污水处理厂最多。
(3)根据图示2000—2004年新建污水处理厂20个,求平均数,即用污水处理厂总数÷(2004-2000),据此解答。21*cnjy*com
【详解】(1)1984年该地区有污水处理厂1个,2004年有污水处理厂95个,这20年来新建了94个污水处理厂。
(2)该地区从1996年到2000年,新建污水处理厂最多。
(3)20÷(2004-2000)
=20÷4
=5(个)
从2000年到2004年,平均每年新建5个污水处理厂。
6.(1)甲分店:187.5万元;乙分店:197.5万元
(2)见详解
【分析】(1)根据公式:平均数=总数÷总份数,由于图中是季度,一个季度是3个月,4个季度是12个月,把销售额加起来,再除以12即可求出平均每个月的销售额。
(2)可以根据折线统计图来关系,看销售额的是增加还是降低来说明。(说法合理即可)
【详解】(1)(700+500+450+600)÷12
=2250÷12
=187.5(万元)
(620+430+570+750)÷12
=2370÷12
=197.5(万元)
答:甲分店平均每个月的销售额是187.5万元,乙分店平均每个月的销售额是197.5万元。
(2)甲分店前三个季度的销售额逐渐下降,到最后一季度的销售额开始增加;乙分店的销售额前两个季度开始下降,之后的两个季度销售额是逐渐增加的。(说法合理即可)
7.(1)一(2)2023(3)2023(4)
【分析】(1)观察这个折线统计图,分别求出两个工程四年产值增长多少,再比较大小,即可求出哪个工厂的产值增长得比较快;【出处:21教育名师】
(2)观察二厂的产值折线图,分别计算每两个相邻年份间的产值的差,比较后即可得出哪年产值比上一年增长得最多;
(3)分别计算每一年度两个厂子的产值的差,比较后即可得出哪年两厂的产值差最大;
(4)求一个数占另一个数的几分之几,用这个数除以另一个数,据此用一厂2022年的产值除以一厂2023年的产值解答。【版权所有:21教育】
【详解】(1)一厂的产值四年间增加了1800-400=1400(万元),二厂的产值四年间增加了910-400=510(万元),因为1400万元>510万元,所以一厂产值增长得快。
(2)450-400=50(万元),550-450=100(万元),650-550=100(万元),910-650=260(万元),因为50万元<100万元=100万元<260万元,所以二厂2023年产值比上一年增长得最多。
(3)400-400=0(万元),600-450=150(万元),950-550=400(万元),1200-650=550(万元),1800-910=890(万元),因为0万元<150万元<400万元<550万元<890万元,所以2023年两厂产值相差最大。
(4)1200÷1800=
答:一厂2022年的产值占2023年的产值的。
8.(1)1800;2000;
(2)11640辆;1.164万辆;
(3)1940辆
【分析】(1)根据图上1格代表200辆,8月对应点的纵轴数据是1800辆,10月对应点的纵轴数据是2000辆填表。
(2)观察图:7月销售1600辆,8月销售1800辆,9月销售1700辆,10月销售2000辆,11月销售2140辆,12月销售2400辆,相加后再改写成用万作单位的数,就在万位后面点上小数点,化简小数后,在数字后面添上“万”字即可。
(3)用这几个月总量除以6个月即可解答。
【详解】
(1)8月份销售新能源汽车( 1800 )辆,10月份销售新能源汽车( 2000 )辆。
(2)1600+1800+1700+2000+2140+2400=11640(辆)
11640=1.164万
答:7至12月一共销售新能源汽车11640辆。合1.164万辆。
(3)11640÷6=1940(辆)
答:该地7至12月平均每月销售新能源汽车1940辆。
9.(1)23;30;
(2)上升;
(3)小林同学;见详解
【分析】(1)复式折线统计图中,横轴表示时间,纵轴表示数量,实线表示小林一周每天一分钟跳绳的情况,虚线表示小丽一周每天一分钟跳绳的情况,折点位置越高跳绳数量越多,折点位置越低跳绳数量越少;
(2)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线走势向上总体呈现上升趋势,折线走势向下总体呈现下降趋势;
(3)从两条折线的走势分析两位同学的跳绳情况,选择成绩波动较小且呈上升趋势的同学即可。
【详解】(1)小林:218-195=23(个)
小丽:223-193=30(个)
所以,小林同学一分钟跳绳的最高成绩与最低成绩相差23个,小丽同学一分钟跳绳的最高成绩与最低成绩相差30个。
(2)从图中可知,小林同学跳绳的成绩,总体呈现上升趋势。
(3)推荐小林同学,观察复式折线统计图可知,小丽的成绩波动较大,小林的成绩稳定且整体呈现上升趋势。(答案不唯一)
10.(1)见详解;
(2)7;10;
(3)11;12
【分析】(1)复式折线统计图中,横轴表示年龄,纵轴表示身高,单位长度表示10厘米,实线表示小强身高,虚线表示标准身高,根据表格中的数据描出各年龄对应的身高,再依次连接各点并标注数据;
(2)先求出小强身高与标准身高的差,再找出身高差在5厘米以内的年龄段;
(3)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线向上走势越陡身高增长越快,据此解答。
【详解】(1)绘制复式折线统计图如下:
(2)7岁:124-122.8=1.2(厘米)
8岁:132-130=2(厘米)
9岁:136.5-135.4=1.1(厘米)
10岁:145-140.2=4.8(厘米)
11岁:156.5-145.3=11.2(厘米)
12岁:170-151.9=18.1(厘米)
所以,与标准身高比较,同年龄低于或高于5厘米属于正常范围,小强7岁至10岁身高在正常范围内。
(3)观察复式折线统计图可知,小强从11岁到12岁身高增长最快,身高偏高。
11.(1);
(2)小时;
(3)杯
【分析】(1)根据统计图可知,小夏休息时间用了(15-5)分钟,总时间是25分钟;用小夏休息时间除以总时间,即可求出小夏回家途中的休息时间占路上总时间的分率;
(2)用小夏完成语文作业的时间-小时,求出小夏完成数学作业的时间,再加上完成语文作业时间,即可求出小夏回家做作业一共用时间;21世纪教育网版权所有
(3)把这杯牛奶的总量看作单位“1”,先喝了整杯的,即喝了杯;用1-=杯,求出剩下牛奶的量,他发现牛奶凉了,就兑满了热水,又喝了半杯,实际上喝了杯的一半,杯的一半是杯,用先喝的杯再加上杯,即可求出小夏一共喝了多少杯纯牛奶。
【详解】(1)(15-5)÷25
=10÷25
=
答:小夏回家途中的休息时间占路上总时间的。
(2)-+
=-+
=+
=(小时)
答:小夏回家做作业一共用了小时。
(3)1-=(杯)
杯的一半是杯。
+=(杯)
答:小夏一共喝了杯。
12.(1)见详解
(2)2022;2023
(3)2023;445
【分析】(1)观察图片,折线倾斜向上表示呈上升趋势,折线倾斜向下表示呈下降趋势。据此解答。
(2)虚线折线倾斜向上坡度较大的表示销售量上升幅度较大,观察可知,2021到2022及2022到2023的向上倾斜坡度较大,可用它们的差比较大小,即可得解。
(3)可观察各年份上代表燃油车和新能源车的两点距离最接近的表示销售量差距最小,再计算它们的差即可得解。21·cn·jy·com
【详解】(1)答:燃油车在2018年~2023年的销售量总体呈现下降趋势;新能源车在2018年~2023年的销售量总体呈现上升趋势。
(2)(万辆)
(万辆)
在相邻的年份中,新能源车在相邻年份2022年至2023年的销售量上升幅度最大。
(3)(万辆)
燃油车和新能源车2023年的销售量差距最小,相差445万辆。
13.(1)见详解
(2)2022;2023
(3)1150
(4)上升趋势
【分析】(1)根据统计表的数据,绘制完整的折线统计图。
(2)分别求出相邻年份销量差,即可解答。
(3)根据平均数=总数÷数据个数,代入数据计算即可。
(4)根据折线统计图的销售走向进行解答。
【详解】(1)
(2)750-550=200(辆)
1500-750=750(辆)
1800-1500=300(辆)
销量增长最多是2022年到2023年。
在相邻年份中,销量增长最多的是2022年到2023年。
(3)(550+750+1500+1800)÷4
=(1300+1500+1800)÷4
=(2800+1800)÷4
=4600÷4
=1150(辆)
这四年的平均销量有1150辆。
(4)观察统计图可知,整体上看,其销量是呈上升趋势。
14.见详解
【分析】横轴为“年份”,纵轴为“参观人数”。单位长度是2万人,根据表中的数据在折线统计图中描出各年份对应的人数,再依次连接各点并标注数据即可。2·1·c·n·j·y
(1)折线统计图的特点:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。据此解答即可。
(2)观察统计图,折线往上,表示上升趋势;折线往下,表示下降趋势;感想不唯一,合理即可。
【详解】根据分析,作图如下:
(1)答:我发现折线统计图的特点:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
(2)参观科技展览的人数2018年到2019年没有变化,其它几年逐年增加,呈现上升趋势。我的感想是科技展览对中小学生的吸引力增强,科技教育得到了更多的重视。
15.(1)5—6
(2)红星
(3)
【分析】(1)要找出销售服装的淡季月份,就需要从图表中找到销量最低的月份即可;
(2)下半年是指7—12月份,从图中可知,红星服装店7—8月份销售250件, 9—10月份销售400件, 11—12月份销售510件;红光服装店7—8月份销售300件, 9—10月份销售250件, 11—12月份销售580件;从数据可知,红星服装店的销售量逐步增长,而红光服装店在9—10月份销量比7—8月份少,因此,可判断销售增长较稳定的是红星服装店;
(3)9—10月红星服装店销售400件,红光服装店销售250件,用减法求出多出的件数。要求红星服装店的销售量比红光服装店多几分之几,就用多的件数除以红光服装店销售的件数;据此解答即可。
【详解】(1)由图可知:
在5~6月,红星服装店销售了100件,红光服装店销售了200件,都是全年中销量最低的月份。
因此,从图上看,5~6月是销售服装的淡季。
(2)由分析可知:
下半年,销售增长较稳定的是红星服装店。
(3)(400-250)÷250
=150÷250
=
答:9—10月份,红星服装店的销售量比红光服装店多。
16.十一月;七月;销售量变化情况见详解
【分析】看图可知,毛衣的销售量在十一月最大,而衬衫的销售量在七月最大。这是因为温度低时,毛衣销售量会增加,衬衫的销售量会减少,据此解答即可。
【详解】答:毛衣的销售量在十一月最大,衬衫的销售量在七月最大。下半年衬衫的销量呈下降趋势,而毛衣的销量呈上升趋势。这是因为温度的变化,导致的毛衣、衬衫的销售量变化趋势不同。
(分析不唯一)
17.见解答
【分析】(1)观察图例可见,一条实线随站次变化,表示每站“上车”人数;另一条虚线则表示“下车”人数,故应将图例补充为“上车人数”“下车人数”。
(2)从图中读数比较,可发现只有在第六站时,上车人数与下车人数相同;而虚线在第八站达到最高值,说明第八站下车人数最多。
(3)要求“最多时车上有多少乘客”,只需逐站累加(上车人数减下车人数)即可。
【详解】(1)如图:
;
(2)第六站实线与虚线相交,表示上、下车乘客一样多;第八站下车乘客最多;
(3)起始站有2位
第一站:2+9-1=10(位)
第二站:10+11-7=14(位)
第三站:14+12-8=18(位)
第四站:18+10-8=20(位)
第五站:20+13-10=23(位)
第六站:23+14-14=23(位)
第七站:23+13-15=21(位)
第八站:21+12-16=17(位)
第九站:17-13+5=9(位)
23=23>21>20>18>17>14>10>9;最多时载23位乘客。
这辆公交车最多时载23位乘客。
18.(1)40千米
(2)130千米
【分析】折线统计图的横轴代表的是时间,纵轴代表的路程,根据折线统计图可以知道王老师2.5小时行驶了200千米,4小时行驶了350千米。【来源:21cnj*y.co*m】
(1)求王老师一家前2.5小时的速度列式:200÷2.5;求后面(4-2.5)小时的速度列式:(350-200)÷(4-2.5);
要想求出“他们出发30分钟时,离家多少千米?”就要知道此时行驶的速度,再根据路程=速度×时间即可解答,注意要把30分钟转换成小时;
(2)先求出后面(4-2.5)小时的速度,求出后面(4-2.5)小时行驶的路程。王老师2.5小时行驶了200千米,用后面(4-2.5)小时行驶的路程加上200千米,计算出前3个小时的行驶路程,总路程减去已行驶的路程即为距离目的地多少千米。
【详解】(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米。
(2)(350-200)÷(4-2.5)×(3-2.5)
=150÷1.5×0.5
=50(千米)
380-(200+50)
=380-250
=130(千米)
答:离目的地还有130千米。
19.(1)不是;第28届
(2)美国
【分析】(1)观察复式折线统计图,两条折线有升有降,所以不是逐年提高。
两条折线的叉口最小时,说明这一届奥运会上两国金牌数量相差最少。
(2)观察统计图中两条折线的变化趋势,虚线起伏比较大,实线比较平稳,据此解答。
【详解】(1)两个国家的奥运会金牌数量都不是逐年提高的,第28届奥运会上两国金牌数量相差最少。
(2)美国金牌数量变化得较平稳。
20.(1)见详解
(2)16
(3)
(4)8.5毫米
【分析】(1)实线表示2021年,虚线表示2022年,根据统计表中的数据先描点,再顺次连成不同的折线,最后标上数据即可;21cnjy.com
(2)2022年四月份的降水量是50毫米,2021年四月份的降水量是34毫米,用减法即可计算两个年份四月份的降水量增加了多少毫米;21·世纪*教育网
(3)2022年四月份的降水量是32毫米,2021年四月份的降水量是38毫米,根据“求一个数是另一个数的几分之几,用除法计算”,32除以38即可解答;
(4)总数量÷份数=平均数,据此分别计算出两个年份上半年的总降水量,除以6,求出月平均降水量,再把它们相减即可解答。
【详解】(1)如图:
(2)50-34=16(毫米),2022年四月份的降水量比2021年同期增加了16毫米。
(3)32÷38=
则2022年五月份的降水量是2021年同期的。
(4)(19+24+51+50+32+34)÷6
=210÷6
=35(毫米)
(10+12+25+34+38+40)÷6
=159÷6
=26.5(毫米)
35-26.5=8.5(毫米)
答:2021年上半年月平均降水量比2022年上半年月平均降水量少了8.5毫米。
21.(1)20厘米;(2)600平方厘米
【分析】(1)9:04时,长方体水槽内水的体积=水流速度×水流的时间,再根据的逆运算,用水的体积除以长方体的底面积,即可得解,计算前先把单位统一为立方厘米;
(2)停止注水后,上升的水的体积就是长方体铁块的体积,观察可知,铁块完全浸没在水中时,水面的高度是23厘米,用23减20可得铁块浸没时水上升的高度。根据,代入数据先求出上升水的体积,再根据这个长方体铁块的底面积=上升水的体积÷铁块的高,代入数据计算即可。
【详解】(1)9时4分-9时=4(分钟)
9立方分米=9000立方厘米
9000×4=36000(立方厘米)
50×36=1800(平方厘米)
36000÷1800=20(厘米)
答:9:04时,长方体水槽内水面高度是20厘米。
(2)23-20=3(厘米)
1800×3=5400(立方厘米)
5400÷9=600(平方厘米)
答:这个长方体铁块的底面积是600平方厘米。
22.(1)10:00
(2)25千米;33千米
(3)2小时;40千米
【分析】(1)两条线相交于一点,就说明两车相遇了,据此解答;
(2)观察统计图可知:2路车从6:00到10:00,4小时行驶了100千米;4路车从7:00到10:00,3小时行驶了100千米。根据行驶的路程÷行驶的时间=行驶的速度,分别用100除以4、100除以3,即可求出它们各自的速度;21教育网
(3)从统计图中可以看出,4路车7:00发车,9:00时两车行驶的路程相差最多,这时4路车开出了(9-7)小时;2路车行驶了40千米,4路车行驶了80千米,把它们相减即可求出差。
【详解】(1)通过分析可得:2路车与4路车在10:00第二次相遇。
(2)2路车:10:00-6:00=4(小时)
100÷4=25(千米/时)
4路车:10:00-7:00=3(小时)
(千米/时)
答:2路车平均每小时行25千米;4路车平均每小时行33千米。
(3)9:00-7:00=2(小时)
80-40=40(千米)
答:在4路车开出2小时后,两车行驶的路程相差最多,相差40千米。
23.1.2小时
【分析】通过观察统计图可知,货车在(3-0.5)小时内行驶了150千米,根据速度=路程÷时间,可以先求出货车的速度,同时可以计算出货车行驶90千米所用的时间即a的值是1.5小时。
那么轿车在(3-1.5)小时内行驶150千米,根据速度=路程÷时间,可以求出轿车的速度。
最后再根据时间=路程÷速度,分别求出货车、轿车到达乙地各用多少小时,并根据求一个数比另一个少多少,用减法解答。
【详解】货车速度:150÷(3-0.5)
=150÷2.5
=60(千米/时)
a:90÷60=1.5(小时)
轿车速度:150÷(3-1.5)
=150÷1.5
=100(千米/时)
330÷60=5.5(小时)
330÷100=3.3(小时)
5.5+0.5-3.3-1.5
=6-3.3-1.5
=1.2(小时)
答:轿车比货车早1.2小时到达乙地。
【点睛】此题考查的是在理解掌握复式折线统计图的特点及作用的基础上,根据统计图提供的信息,解决有关的实际问题。
24.600千米
【分析】从图中可知:AB两地相距300千米,甲、乙两车分别从A,B两地同时相向匀速行驶,3小时相遇,用300÷3=100千米即求出甲、乙两车的速度和。甲到达B地用了5小时,用300÷5=60千米即求出甲的速度。用100-60=40千米即求出乙的速度。甲到达B地时,乙距离B地40×5=200千米,也就是甲车到达地,此时与乙相距200千米。根据追及时间=路程差÷速度差,用200÷(60-40)=10小时求出甲追上乙的时间,即此时两车同时到达地。这10小时甲行驶的路程是60×10=600千米,也就是B,C两地的距离。
【详解】速度和:300÷3=100(千米)
甲速度:300÷5=60(千米)
乙速度:100-60=40(千米)
40×5÷(60-40)
=200÷20
=10(小时)
60×10=600(千米)
答:B,C两地相距600千米。
【点睛】根据折线统计图,分析出路程时间之间的关系。求出甲追上乙的时间是解此题的关键。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
(核心素养应用意识)第七单元折线统计图(解决问一)-五年级数学下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.如图所示是某家电商场A、B两种品牌电视机2021年月销售量统计图。观察这个折线统计图所呈现的数据,回答下面的问题。
(1)折线统计图适合呈现数据的( )情况。
(2)如果你是商场的经理,你能从上面的复式折线统计图中得到哪些信息?这些信息对你有什么帮助?
2.下面是2023年某市某天不同时间空气质量指数统计表。
时间 7时 10时 13时 16时 19时
空气质量指数 155 198 210 195 180
(1)如果想清晰地看出不同时间空气质量指数的变化情况,应该绘制( )统计图。请根据提供的数据完成这个统计图。
(2)你能描述这一天中空气质量指数的变化趋势吗?
3.晶晶和乐乐参加一分钟踢毽子比赛,提前一周进行训练,两位同学每天测试的成绩如下表,请你根据表中数据,完成下面的折线统计图。
(1)晶晶和乐乐第( )次的测试成绩相同,是( )个。
(2)观察统计图,晶晶和乐乐踢毽子的训练成绩总体呈现什么变化趋势?请你分析谁的进步更大?
(3)你能预测两个人的比赛成绩吗?请说出理由。
4.下图是电脑城2020年1——5月份甲、乙两种品牌电脑的销售情况统计图。
(1)根据条形统计图绘制折线统计图。
(2)从图中可以看出( )比( )销售情况好。
5.下面是我国某地区20年来污水处理厂的数量统计图。
看统计图表回答问题:
(1)1984年该地区有污水处理厂( )个,2004年有污水处理厂( )个,这20年来新建了( )个污水处理厂。
(2)该地区从( )年到( )年,新建污水处理厂最多。
(3)从2000年到2004年,平均每年新建( )个污水处理厂。
6.下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图,请你看图回答问题。
(1)甲、乙两个分店平均每个月的销售额各是多少万元?
(2)说说两个店销售额的变化情况。
7.看图回答问题。
(1)( )厂产值增长得快。
(2)二厂( )年产值比上一年增长得最多。
(3)( )年两厂产值相差最大。
(4)一厂2022年的产值占2023年的产值的几分之几?
8.如图是某地2022年下半年新能源汽车销售情况统计图。
(1)8月份销售新能源汽车( )辆,10月份销售新能源汽车( )辆。
(2)7至12月一共销售新能源汽车多少辆?合多少万辆?
(3)该地7至12月平均每月销售新能源汽车多少辆?
9.五(2)班要在小林和小丽两位同学中,选出一名同学代表班级参加学校举行的跳绳比赛。下面是他们一周每天一分钟跳绳的情况记录,请根据图中信息解决下列问题。
(1)从图中可以看出,小林同学一分钟跳绳的最高成绩与最低成绩相差( )个;小丽同学一分钟跳绳的最高成绩与最低成绩相差( )个。【来源:21·世纪·教育·网】
(2)从图中可知,小林同学跳绳的成绩,总体呈现( )趋势。(填“上升”或“下降”)
(3)你会推荐哪位同学代表班级参加一分钟跳绳比赛?说说你的理由。
10.下面是小强7-12岁每年的身高与同龄男童标准身高的对比统计表。
年龄(岁)身高(厘米) 7 8 9 10 11 12
标准身高 124 130 135.4 140.2 145.3 151.9
小强身高 122.8 132 136.5 145 156.5 170
(1)根据表中数据,补充完折线统计图。
(2)与标准身高比较,同年龄低于或高于5厘米属于正常范围,小强( )岁至( )岁身高在正常范围内。www-2-1-cnjy-com
(3)小强从( )岁到( )岁身高增长最快,身高偏高。
11.学校放学时,小夏直接走路回家,行程情况统计如下图所示。到家后,小夏倒了一杯纯牛奶,先喝了整杯的,再开始做语文作业,用了小时完成;休息了一会儿,他发现牛奶凉了,就兑满了热水,又喝了半杯后,开始写数学作业,结果比完成语文作业少用了小时。然后,他就愉快地出去玩了。
(1)小夏回家途中的休息时间占路上总时间的几分之几?
(2)小夏回家做作业一共用了多少小时?
(3)在这整个过程中,小夏一共喝了多少杯纯牛奶?
12.小华了解到2018年~2023年全国燃油车和新能源车销售量情况如下图。请根据图中信息回答问题。21*cnjy*com
2018年~2023年全国燃油车和新能源车销售量情况统计图
①从上图可看出,燃油车和新能源车在2018年~2023年的销售量总体呈现怎样的趋势?
②在相邻的年份中,新能源车在相邻年份( )年至( )年的销售量上升幅度最大。
③燃油车和新能源车( )年的销售量差距最小,相差( )万辆。
13.某汽车销售店2021年至2024年销售情况如下表。
年份 2021 2022 2023 2024
数量(辆) 550 750 1500 1800
(1)根据上表的数据,把下面的折线统计图补充完整。
(2)在相邻年份中,销量增长最多的是(______年到______年)。
(3)这四年的平均销量有( )辆。
(4)整体上看,其销售情况的趋势怎样?
14.将下图中的条形统计图改画成折线统计图。
(1)你发现折线统计图有什么特点?
(2)中小学生参观科技展览的人数有什么变化?你有什么感想?
15.下面是两个服装店2023年的销售情况统计图。
(1)从图上看,( )月是销售服装的淡季。
(2)下半年,销售增长较稳定的是( )服装店。
(3)9—10月份,红星服装店的销售量比红光服装店多几分之几?
16.下面是某百货商店2022年下半年毛衣和衬衫销售情况统计图。看图说出毛衣的销售量在哪个月最大?衬衫呢?你能分析它们的销售量变化情况吗?
17.如图是一辆公交车从起始站至终点站的行驶过程中乘客上下车情况统计图。
(1)请把统计图中的图例补充完整。
(2)从图中可以看出,第( )站上车乘客和下车乘客一样多,第( )站下车乘客最多。
(3)这辆公交车最多时载( )位乘客。
18.暑假,王老师一家自驾去离家380千米的景点玩,如图是他们离家的距离与汽车行驶时间之间的关系图。
(1)王老师一家出发30分钟时,离家多少千米?
(2)出发后3小时,距离目的地多少千米?
19.下图是第25~30届奥运会上中国和美国获金牌数量的统计图。
(1)两个国家的奥运会金牌数量是逐年提高的吗?哪一届奥运会上两国金牌数量相差最少?
(2)中国和美国哪个国家金牌数量变化得较平稳?
20.某地2021年上半年每月降水量和2022年上半年每月降水量情况如下表:
降水量月份 一月 二月 三月 四月 五月 六月
2022年 19 24 51 50 32 34
2021年 10 12 25 34 38 40
(1)根据上表中的数据制成复式折线统计图。
(2)2022年四月份的降水量比2021年同期增加了( )毫米。
(3)2022年五月份的降水量是2021年同期的。
(4)2021年上半年月平均降水量比2022年上半年月平均降水量少了多少毫米?
21.如下图所示,有一个无水的长方体水槽,一个水龙头从9:00开始向水槽内注水,水流速度为9立方分米/分,9:04停止注水。接着在水槽内放入一个高为9厘米的长方体铁块,使其全部浸没在水中。从开始注水到铁块全部浸没在水中,水槽的水面高度变化情况如图中所示。21教育名师原创作品
(1)9:04时,长方体水槽内水面高度是多少厘米?
(2)这个长方体铁块的底面积是多少平方厘米?
22.下面是从同一车站发出的两辆车的运行情况。
(1)2路车与4路车在( )第二次相遇。
(2)2路车和4路车平均每小时各行多少千米?
(3)在4路车开出几小时后,两车行驶的路程相差最多?相差多少千米?
23.一辆货车从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地。已知甲乙两地的路程是330千米,货车在途中停留半小时。两车离甲地的路程与时间关系如图所示。轿车比货车早几小时到达乙地?2-1-c-n-j-y
24.甲、乙两车分别从A,B两地同时相向匀速行驶。当乙车到达地后,继续保持原速向远离的方向行驶,而甲车到达地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达地。设两车行驶的时间为(小时),两车之间的距离为(千米),与之间的关系如图所示,则B,C两地相距多少千米。
《(核心素养应用意识)第七单元折线统计图(解决问一)-五年级数学下册人教版》参考答案
1.(1)增减变化;
(2)从复式折线统计图中可以看出2021年A品牌电视机的销售量总体呈下降趋势;B品牌电视机的销售量总体比较稳定,并呈上升趋势,应少进A品牌电视机。
【分析】(1)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
(2)实线表示A品牌的销售情况,虚线表示B品牌的销售情况,通过观察两条线的走向,实线呈下降趋势,虚线呈上升趋势,但还是比较稳定。
【详解】(1)折线统计图适合呈现数据的增减变化情况。
(2)从复式折线统计图中可以看出2021年A品牌电视机的销售量总体呈下降趋势;B品牌电视机的销售量总体比较稳定,并呈上升趋势,应少进A品牌电视机。
2.(1)折线;
图见详解
(2)从7时到13时,空气质量指数逐渐上升,从13时到19时,空气质量逐渐下降(答案不唯一)
【分析】(1)根据条形统计图的特点:能够反应数据的多少;折线统计图:可以看出数据的增减变化情况,由于要反应空气质量指数的变化情况,应绘制折线统计图,先描点,再连线即可画出统计图;
(2)根据图中数据,在13时空气质量指数最高,从7时到13时逐渐上升,13时之后开始下降,说法合理即可;据此即可解答。
【详解】(1)如果想清晰地看出不同时间空气质量指数的变化情况,应该绘制折线统计图。
如图:
(2)答:从7时到13时,空气质量指数逐渐上升,从13时到19时,空气质量逐渐下降。(答案不唯一)
3.图见详解
(1)3;38
(2)见详解(答案不唯一)
(3)见详解(答案不唯一)
【分析】画图时,横轴代表测试次数,纵轴代表成绩(下),根据表格所给数据,看横轴描出纵轴的对应点,再将各点依次连接可作出统计图;
(1)两条折线的交点对应的横轴,就是测试成绩相同的次数;
(2)折线走向是上升的则成绩上升,折线走向下降则成绩下降,折线越陡成绩变化越大;
(3)根据图中折线走向、表中次数来预测二人成绩。
【详解】
(1)有图表可知:
晶晶和乐乐第3次的测试成绩相同,是38个。
(2)答:晶晶的成绩一直呈上升趋势,乐乐的成绩有下降的时候,并且晶晶的成绩大多数高于乐乐的成绩,所以,晶晶的成绩进步更大。(答案不唯一,合理即可)
(3)答:预测两个人的比赛成绩总体呈上升趋势均可能大于40下,晶晶的成绩好于乐乐的成绩,且晶晶的成绩较稳定。(答案不唯一,合理即可)www.21-cn-jy.com
4.(1)见详解;(2)甲品牌;乙品牌
【分析】(1)根据条形统计图,分别描出相应的点,再依次连接即可;用实线表示甲品牌的销售情况,用虚线表示乙品牌的销售情况。
(2)条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;通过观察折线统计图的走向,实线高于虚线,所以甲品牌比乙品牌的销售情况好。
【详解】(1)如图:
(2)通过观察可知,甲品牌比乙品牌的销售情况好。
5.(1) 1 95 94
(2) 1996 2000
(3)5
【分析】(1)根据图示,1984年对应污水处理厂1个,2004年有污水处理厂95个。新建的数量就是2004年的数量减去1984年的数量,即95-1=94(个)
(2)根据图示,1984—1988年新建污水处理厂8-1=7(个);
1988年—1992年新建污水处理厂19-8=11(个);
1992—1996年新建污水处理厂36-19=17(个);
1996—2000年新建污水处理厂75-36=39(个);
2000—2004年新建污水处理厂95-75=20(个);
综上区间数据1996年—2000年新建污水处理厂最多。
(3)根据图示2000—2004年新建污水处理厂20个,求平均数,即用污水处理厂总数÷(2004-2000),据此解答。21*cnjy*com
【详解】(1)1984年该地区有污水处理厂1个,2004年有污水处理厂95个,这20年来新建了94个污水处理厂。
(2)该地区从1996年到2000年,新建污水处理厂最多。
(3)20÷(2004-2000)
=20÷4
=5(个)
从2000年到2004年,平均每年新建5个污水处理厂。
6.(1)甲分店:187.5万元;乙分店:197.5万元
(2)见详解
【分析】(1)根据公式:平均数=总数÷总份数,由于图中是季度,一个季度是3个月,4个季度是12个月,把销售额加起来,再除以12即可求出平均每个月的销售额。
(2)可以根据折线统计图来关系,看销售额的是增加还是降低来说明。(说法合理即可)
【详解】(1)(700+500+450+600)÷12
=2250÷12
=187.5(万元)
(620+430+570+750)÷12
=2370÷12
=197.5(万元)
答:甲分店平均每个月的销售额是187.5万元,乙分店平均每个月的销售额是197.5万元。
(2)甲分店前三个季度的销售额逐渐下降,到最后一季度的销售额开始增加;乙分店的销售额前两个季度开始下降,之后的两个季度销售额是逐渐增加的。(说法合理即可)
7.(1)一(2)2023(3)2023(4)
【分析】(1)观察这个折线统计图,分别求出两个工程四年产值增长多少,再比较大小,即可求出哪个工厂的产值增长得比较快;【出处:21教育名师】
(2)观察二厂的产值折线图,分别计算每两个相邻年份间的产值的差,比较后即可得出哪年产值比上一年增长得最多;
(3)分别计算每一年度两个厂子的产值的差,比较后即可得出哪年两厂的产值差最大;
(4)求一个数占另一个数的几分之几,用这个数除以另一个数,据此用一厂2022年的产值除以一厂2023年的产值解答。【版权所有:21教育】
【详解】(1)一厂的产值四年间增加了1800-400=1400(万元),二厂的产值四年间增加了910-400=510(万元),因为1400万元>510万元,所以一厂产值增长得快。
(2)450-400=50(万元),550-450=100(万元),650-550=100(万元),910-650=260(万元),因为50万元<100万元=100万元<260万元,所以二厂2023年产值比上一年增长得最多。
(3)400-400=0(万元),600-450=150(万元),950-550=400(万元),1200-650=550(万元),1800-910=890(万元),因为0万元<150万元<400万元<550万元<890万元,所以2023年两厂产值相差最大。
(4)1200÷1800=
答:一厂2022年的产值占2023年的产值的。
8.(1)1800;2000;
(2)11640辆;1.164万辆;
(3)1940辆
【分析】(1)根据图上1格代表200辆,8月对应点的纵轴数据是1800辆,10月对应点的纵轴数据是2000辆填表。
(2)观察图:7月销售1600辆,8月销售1800辆,9月销售1700辆,10月销售2000辆,11月销售2140辆,12月销售2400辆,相加后再改写成用万作单位的数,就在万位后面点上小数点,化简小数后,在数字后面添上“万”字即可。
(3)用这几个月总量除以6个月即可解答。
【详解】
(1)8月份销售新能源汽车( 1800 )辆,10月份销售新能源汽车( 2000 )辆。
(2)1600+1800+1700+2000+2140+2400=11640(辆)
11640=1.164万
答:7至12月一共销售新能源汽车11640辆。合1.164万辆。
(3)11640÷6=1940(辆)
答:该地7至12月平均每月销售新能源汽车1940辆。
9.(1)23;30;
(2)上升;
(3)小林同学;见详解
【分析】(1)复式折线统计图中,横轴表示时间,纵轴表示数量,实线表示小林一周每天一分钟跳绳的情况,虚线表示小丽一周每天一分钟跳绳的情况,折点位置越高跳绳数量越多,折点位置越低跳绳数量越少;
(2)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线走势向上总体呈现上升趋势,折线走势向下总体呈现下降趋势;
(3)从两条折线的走势分析两位同学的跳绳情况,选择成绩波动较小且呈上升趋势的同学即可。
【详解】(1)小林:218-195=23(个)
小丽:223-193=30(个)
所以,小林同学一分钟跳绳的最高成绩与最低成绩相差23个,小丽同学一分钟跳绳的最高成绩与最低成绩相差30个。
(2)从图中可知,小林同学跳绳的成绩,总体呈现上升趋势。
(3)推荐小林同学,观察复式折线统计图可知,小丽的成绩波动较大,小林的成绩稳定且整体呈现上升趋势。(答案不唯一)
10.(1)见详解;
(2)7;10;
(3)11;12
【分析】(1)复式折线统计图中,横轴表示年龄,纵轴表示身高,单位长度表示10厘米,实线表示小强身高,虚线表示标准身高,根据表格中的数据描出各年龄对应的身高,再依次连接各点并标注数据;
(2)先求出小强身高与标准身高的差,再找出身高差在5厘米以内的年龄段;
(3)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线向上走势越陡身高增长越快,据此解答。
【详解】(1)绘制复式折线统计图如下:
(2)7岁:124-122.8=1.2(厘米)
8岁:132-130=2(厘米)
9岁:136.5-135.4=1.1(厘米)
10岁:145-140.2=4.8(厘米)
11岁:156.5-145.3=11.2(厘米)
12岁:170-151.9=18.1(厘米)
所以,与标准身高比较,同年龄低于或高于5厘米属于正常范围,小强7岁至10岁身高在正常范围内。
(3)观察复式折线统计图可知,小强从11岁到12岁身高增长最快,身高偏高。
11.(1);
(2)小时;
(3)杯
【分析】(1)根据统计图可知,小夏休息时间用了(15-5)分钟,总时间是25分钟;用小夏休息时间除以总时间,即可求出小夏回家途中的休息时间占路上总时间的分率;
(2)用小夏完成语文作业的时间-小时,求出小夏完成数学作业的时间,再加上完成语文作业时间,即可求出小夏回家做作业一共用时间;21世纪教育网版权所有
(3)把这杯牛奶的总量看作单位“1”,先喝了整杯的,即喝了杯;用1-=杯,求出剩下牛奶的量,他发现牛奶凉了,就兑满了热水,又喝了半杯,实际上喝了杯的一半,杯的一半是杯,用先喝的杯再加上杯,即可求出小夏一共喝了多少杯纯牛奶。
【详解】(1)(15-5)÷25
=10÷25
=
答:小夏回家途中的休息时间占路上总时间的。
(2)-+
=-+
=+
=(小时)
答:小夏回家做作业一共用了小时。
(3)1-=(杯)
杯的一半是杯。
+=(杯)
答:小夏一共喝了杯。
12.(1)见详解
(2)2022;2023
(3)2023;445
【分析】(1)观察图片,折线倾斜向上表示呈上升趋势,折线倾斜向下表示呈下降趋势。据此解答。
(2)虚线折线倾斜向上坡度较大的表示销售量上升幅度较大,观察可知,2021到2022及2022到2023的向上倾斜坡度较大,可用它们的差比较大小,即可得解。
(3)可观察各年份上代表燃油车和新能源车的两点距离最接近的表示销售量差距最小,再计算它们的差即可得解。21·cn·jy·com
【详解】(1)答:燃油车在2018年~2023年的销售量总体呈现下降趋势;新能源车在2018年~2023年的销售量总体呈现上升趋势。
(2)(万辆)
(万辆)
在相邻的年份中,新能源车在相邻年份2022年至2023年的销售量上升幅度最大。
(3)(万辆)
燃油车和新能源车2023年的销售量差距最小,相差445万辆。
13.(1)见详解
(2)2022;2023
(3)1150
(4)上升趋势
【分析】(1)根据统计表的数据,绘制完整的折线统计图。
(2)分别求出相邻年份销量差,即可解答。
(3)根据平均数=总数÷数据个数,代入数据计算即可。
(4)根据折线统计图的销售走向进行解答。
【详解】(1)
(2)750-550=200(辆)
1500-750=750(辆)
1800-1500=300(辆)
销量增长最多是2022年到2023年。
在相邻年份中,销量增长最多的是2022年到2023年。
(3)(550+750+1500+1800)÷4
=(1300+1500+1800)÷4
=(2800+1800)÷4
=4600÷4
=1150(辆)
这四年的平均销量有1150辆。
(4)观察统计图可知,整体上看,其销量是呈上升趋势。
14.见详解
【分析】横轴为“年份”,纵轴为“参观人数”。单位长度是2万人,根据表中的数据在折线统计图中描出各年份对应的人数,再依次连接各点并标注数据即可。2·1·c·n·j·y
(1)折线统计图的特点:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。据此解答即可。
(2)观察统计图,折线往上,表示上升趋势;折线往下,表示下降趋势;感想不唯一,合理即可。
【详解】根据分析,作图如下:
(1)答:我发现折线统计图的特点:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
(2)参观科技展览的人数2018年到2019年没有变化,其它几年逐年增加,呈现上升趋势。我的感想是科技展览对中小学生的吸引力增强,科技教育得到了更多的重视。
15.(1)5—6
(2)红星
(3)
【分析】(1)要找出销售服装的淡季月份,就需要从图表中找到销量最低的月份即可;
(2)下半年是指7—12月份,从图中可知,红星服装店7—8月份销售250件, 9—10月份销售400件, 11—12月份销售510件;红光服装店7—8月份销售300件, 9—10月份销售250件, 11—12月份销售580件;从数据可知,红星服装店的销售量逐步增长,而红光服装店在9—10月份销量比7—8月份少,因此,可判断销售增长较稳定的是红星服装店;
(3)9—10月红星服装店销售400件,红光服装店销售250件,用减法求出多出的件数。要求红星服装店的销售量比红光服装店多几分之几,就用多的件数除以红光服装店销售的件数;据此解答即可。
【详解】(1)由图可知:
在5~6月,红星服装店销售了100件,红光服装店销售了200件,都是全年中销量最低的月份。
因此,从图上看,5~6月是销售服装的淡季。
(2)由分析可知:
下半年,销售增长较稳定的是红星服装店。
(3)(400-250)÷250
=150÷250
=
答:9—10月份,红星服装店的销售量比红光服装店多。
16.十一月;七月;销售量变化情况见详解
【分析】看图可知,毛衣的销售量在十一月最大,而衬衫的销售量在七月最大。这是因为温度低时,毛衣销售量会增加,衬衫的销售量会减少,据此解答即可。
【详解】答:毛衣的销售量在十一月最大,衬衫的销售量在七月最大。下半年衬衫的销量呈下降趋势,而毛衣的销量呈上升趋势。这是因为温度的变化,导致的毛衣、衬衫的销售量变化趋势不同。
(分析不唯一)
17.见解答
【分析】(1)观察图例可见,一条实线随站次变化,表示每站“上车”人数;另一条虚线则表示“下车”人数,故应将图例补充为“上车人数”“下车人数”。
(2)从图中读数比较,可发现只有在第六站时,上车人数与下车人数相同;而虚线在第八站达到最高值,说明第八站下车人数最多。
(3)要求“最多时车上有多少乘客”,只需逐站累加(上车人数减下车人数)即可。
【详解】(1)如图:
;
(2)第六站实线与虚线相交,表示上、下车乘客一样多;第八站下车乘客最多;
(3)起始站有2位
第一站:2+9-1=10(位)
第二站:10+11-7=14(位)
第三站:14+12-8=18(位)
第四站:18+10-8=20(位)
第五站:20+13-10=23(位)
第六站:23+14-14=23(位)
第七站:23+13-15=21(位)
第八站:21+12-16=17(位)
第九站:17-13+5=9(位)
23=23>21>20>18>17>14>10>9;最多时载23位乘客。
这辆公交车最多时载23位乘客。
18.(1)40千米
(2)130千米
【分析】折线统计图的横轴代表的是时间,纵轴代表的路程,根据折线统计图可以知道王老师2.5小时行驶了200千米,4小时行驶了350千米。【来源:21cnj*y.co*m】
(1)求王老师一家前2.5小时的速度列式:200÷2.5;求后面(4-2.5)小时的速度列式:(350-200)÷(4-2.5);
要想求出“他们出发30分钟时,离家多少千米?”就要知道此时行驶的速度,再根据路程=速度×时间即可解答,注意要把30分钟转换成小时;
(2)先求出后面(4-2.5)小时的速度,求出后面(4-2.5)小时行驶的路程。王老师2.5小时行驶了200千米,用后面(4-2.5)小时行驶的路程加上200千米,计算出前3个小时的行驶路程,总路程减去已行驶的路程即为距离目的地多少千米。
【详解】(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米。
(2)(350-200)÷(4-2.5)×(3-2.5)
=150÷1.5×0.5
=50(千米)
380-(200+50)
=380-250
=130(千米)
答:离目的地还有130千米。
19.(1)不是;第28届
(2)美国
【分析】(1)观察复式折线统计图,两条折线有升有降,所以不是逐年提高。
两条折线的叉口最小时,说明这一届奥运会上两国金牌数量相差最少。
(2)观察统计图中两条折线的变化趋势,虚线起伏比较大,实线比较平稳,据此解答。
【详解】(1)两个国家的奥运会金牌数量都不是逐年提高的,第28届奥运会上两国金牌数量相差最少。
(2)美国金牌数量变化得较平稳。
20.(1)见详解
(2)16
(3)
(4)8.5毫米
【分析】(1)实线表示2021年,虚线表示2022年,根据统计表中的数据先描点,再顺次连成不同的折线,最后标上数据即可;21cnjy.com
(2)2022年四月份的降水量是50毫米,2021年四月份的降水量是34毫米,用减法即可计算两个年份四月份的降水量增加了多少毫米;21·世纪*教育网
(3)2022年四月份的降水量是32毫米,2021年四月份的降水量是38毫米,根据“求一个数是另一个数的几分之几,用除法计算”,32除以38即可解答;
(4)总数量÷份数=平均数,据此分别计算出两个年份上半年的总降水量,除以6,求出月平均降水量,再把它们相减即可解答。
【详解】(1)如图:
(2)50-34=16(毫米),2022年四月份的降水量比2021年同期增加了16毫米。
(3)32÷38=
则2022年五月份的降水量是2021年同期的。
(4)(19+24+51+50+32+34)÷6
=210÷6
=35(毫米)
(10+12+25+34+38+40)÷6
=159÷6
=26.5(毫米)
35-26.5=8.5(毫米)
答:2021年上半年月平均降水量比2022年上半年月平均降水量少了8.5毫米。
21.(1)20厘米;(2)600平方厘米
【分析】(1)9:04时,长方体水槽内水的体积=水流速度×水流的时间,再根据的逆运算,用水的体积除以长方体的底面积,即可得解,计算前先把单位统一为立方厘米;
(2)停止注水后,上升的水的体积就是长方体铁块的体积,观察可知,铁块完全浸没在水中时,水面的高度是23厘米,用23减20可得铁块浸没时水上升的高度。根据,代入数据先求出上升水的体积,再根据这个长方体铁块的底面积=上升水的体积÷铁块的高,代入数据计算即可。
【详解】(1)9时4分-9时=4(分钟)
9立方分米=9000立方厘米
9000×4=36000(立方厘米)
50×36=1800(平方厘米)
36000÷1800=20(厘米)
答:9:04时,长方体水槽内水面高度是20厘米。
(2)23-20=3(厘米)
1800×3=5400(立方厘米)
5400÷9=600(平方厘米)
答:这个长方体铁块的底面积是600平方厘米。
22.(1)10:00
(2)25千米;33千米
(3)2小时;40千米
【分析】(1)两条线相交于一点,就说明两车相遇了,据此解答;
(2)观察统计图可知:2路车从6:00到10:00,4小时行驶了100千米;4路车从7:00到10:00,3小时行驶了100千米。根据行驶的路程÷行驶的时间=行驶的速度,分别用100除以4、100除以3,即可求出它们各自的速度;21教育网
(3)从统计图中可以看出,4路车7:00发车,9:00时两车行驶的路程相差最多,这时4路车开出了(9-7)小时;2路车行驶了40千米,4路车行驶了80千米,把它们相减即可求出差。
【详解】(1)通过分析可得:2路车与4路车在10:00第二次相遇。
(2)2路车:10:00-6:00=4(小时)
100÷4=25(千米/时)
4路车:10:00-7:00=3(小时)
(千米/时)
答:2路车平均每小时行25千米;4路车平均每小时行33千米。
(3)9:00-7:00=2(小时)
80-40=40(千米)
答:在4路车开出2小时后,两车行驶的路程相差最多,相差40千米。
23.1.2小时
【分析】通过观察统计图可知,货车在(3-0.5)小时内行驶了150千米,根据速度=路程÷时间,可以先求出货车的速度,同时可以计算出货车行驶90千米所用的时间即a的值是1.5小时。
那么轿车在(3-1.5)小时内行驶150千米,根据速度=路程÷时间,可以求出轿车的速度。
最后再根据时间=路程÷速度,分别求出货车、轿车到达乙地各用多少小时,并根据求一个数比另一个少多少,用减法解答。
【详解】货车速度:150÷(3-0.5)
=150÷2.5
=60(千米/时)
a:90÷60=1.5(小时)
轿车速度:150÷(3-1.5)
=150÷1.5
=100(千米/时)
330÷60=5.5(小时)
330÷100=3.3(小时)
5.5+0.5-3.3-1.5
=6-3.3-1.5
=1.2(小时)
答:轿车比货车早1.2小时到达乙地。
【点睛】此题考查的是在理解掌握复式折线统计图的特点及作用的基础上,根据统计图提供的信息,解决有关的实际问题。
24.600千米
【分析】从图中可知:AB两地相距300千米,甲、乙两车分别从A,B两地同时相向匀速行驶,3小时相遇,用300÷3=100千米即求出甲、乙两车的速度和。甲到达B地用了5小时,用300÷5=60千米即求出甲的速度。用100-60=40千米即求出乙的速度。甲到达B地时,乙距离B地40×5=200千米,也就是甲车到达地,此时与乙相距200千米。根据追及时间=路程差÷速度差,用200÷(60-40)=10小时求出甲追上乙的时间,即此时两车同时到达地。这10小时甲行驶的路程是60×10=600千米,也就是B,C两地的距离。
【详解】速度和:300÷3=100(千米)
甲速度:300÷5=60(千米)
乙速度:100-60=40(千米)
40×5÷(60-40)
=200÷20
=10(小时)
60×10=600(千米)
答:B,C两地相距600千米。
【点睛】根据折线统计图,分析出路程时间之间的关系。求出甲追上乙的时间是解此题的关键。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
