(核心素养应用意识)第七单元折线统计图(解决问题二)(含解析)-五年级数学下册人教版
文档属性
| 名称 | (核心素养应用意识)第七单元折线统计图(解决问题二)(含解析)-五年级数学下册人教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览

文档简介
/ 让教学更有效 精品试卷 | 数学学科
第七单元折线统计图
学校:___________姓名:___________班级:___________考号:___________
一、解答题
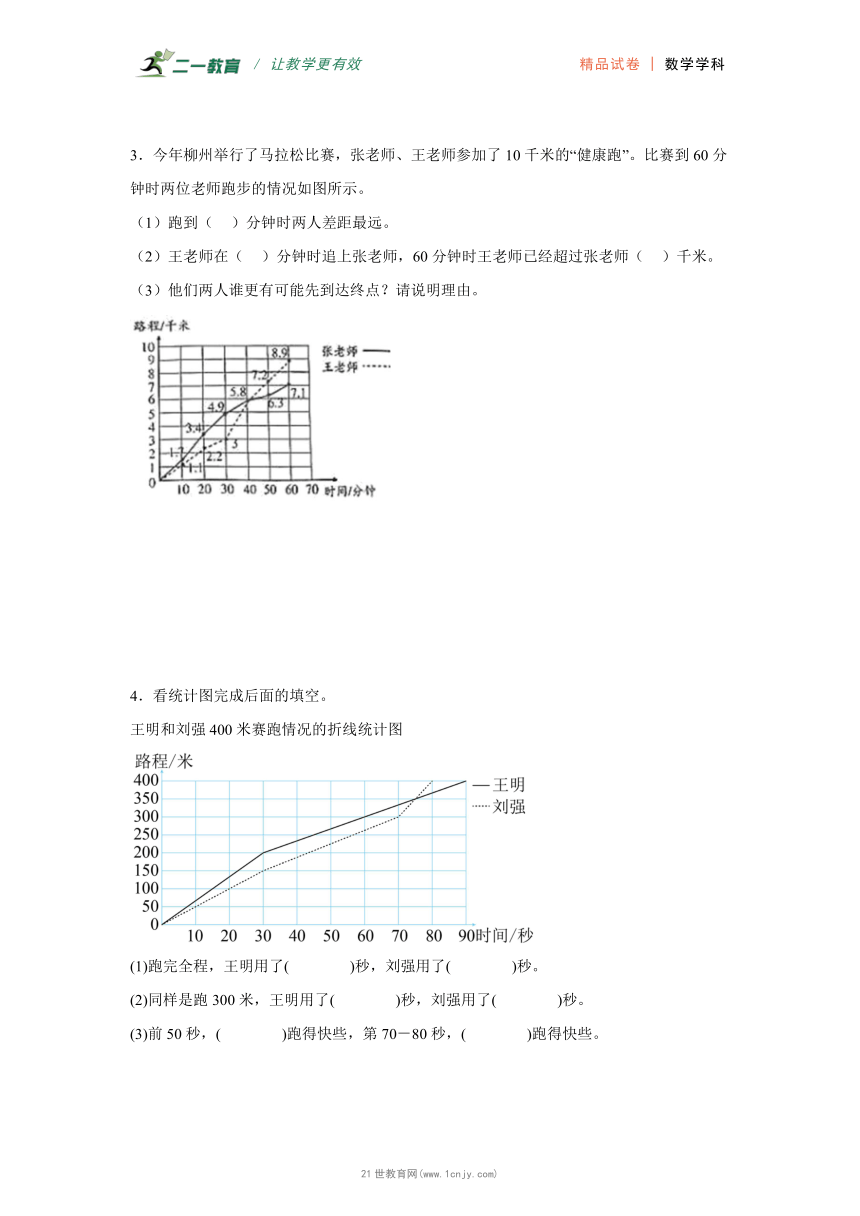
1.观察统计图,回答问题。
北京市2018-2022年居民人均可支配收入和人均消费支出统计图
(1)北京市居民人均可支配收入哪一年增长最快?增长了多少元?
(2)北京市居民人均可支配收入和人均消费支出相比,哪一年的差距最大?相差了多少元?
(3)北京市居民人均可支配收入和人均消费支出呈现怎样的变化趋势?通过这些数据,请你提出一个想继续研究的数学问题。
2.下面是北海、南充两个市2020年上半年月平均气温变化情况统计图,请你回答下面问题。
(1)南充市2020年上半年月平均气温是怎样变化的?
(2)南充市和北海市2020年上半年平均气温变化情况有什么区别?
(3)如果让你选择居住的城市,你选择哪座城市,为什么?
3.今年柳州举行了马拉松比赛,张老师、王老师参加了10千米的“健康跑”。比赛到60分钟时两位老师跑步的情况如图所示。
(1)跑到( )分钟时两人差距最远。
(2)王老师在( )分钟时追上张老师,60分钟时王老师已经超过张老师( )千米。
(3)他们两人谁更有可能先到达终点?请说明理由。
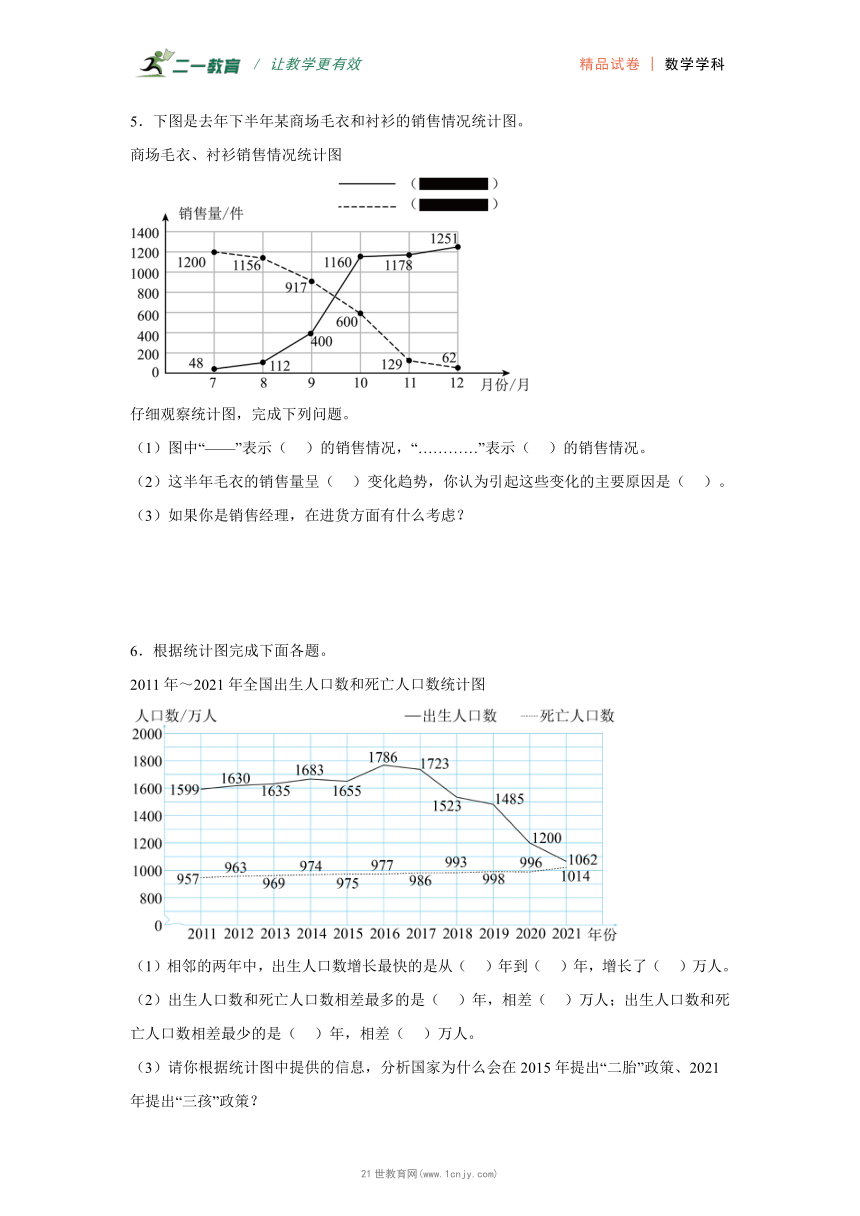
4.看统计图完成后面的填空。
王明和刘强400米赛跑情况的折线统计图
(1)跑完全程,王明用了( )秒,刘强用了( )秒。
(2)同样是跑300米,王明用了( )秒,刘强用了( )秒。
(3)前50秒,( )跑得快些,第70-80秒,( )跑得快些。
5.下图是去年下半年某商场毛衣和衬衫的销售情况统计图。
商场毛衣、衬衫销售情况统计图
仔细观察统计图,完成下列问题。
(1)图中“——”表示( )的销售情况,“…………”表示( )的销售情况。
(2)这半年毛衣的销售量呈( )变化趋势,你认为引起这些变化的主要原因是( )。
(3)如果你是销售经理,在进货方面有什么考虑?
6.根据统计图完成下面各题。
2011年~2021年全国出生人口数和死亡人口数统计图
(1)相邻的两年中,出生人口数增长最快的是从( )年到( )年,增长了( )万人。
(2)出生人口数和死亡人口数相差最多的是( )年,相差( )万人;出生人口数和死亡人口数相差最少的是( )年,相差( )万人。21世纪教育网版权所有
(3)请你根据统计图中提供的信息,分析国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策?
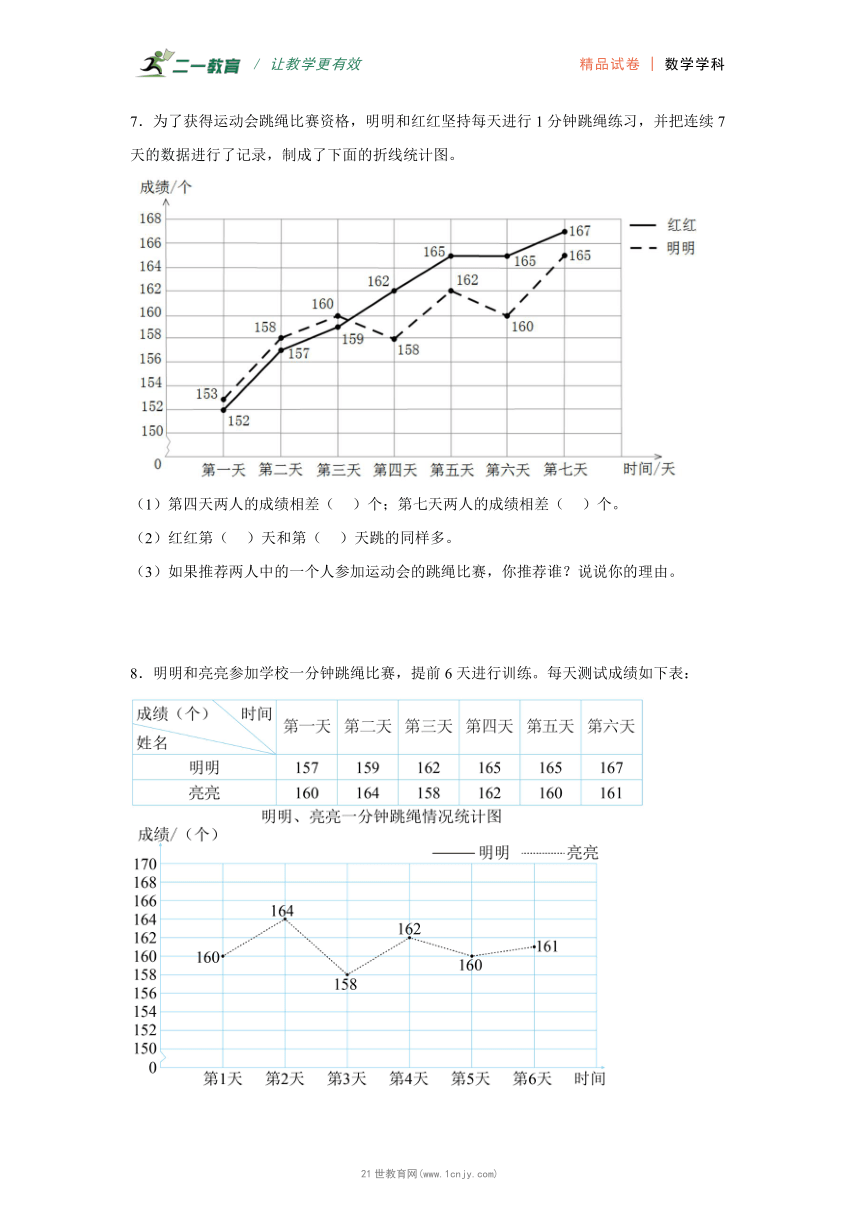
7.为了获得运动会跳绳比赛资格,明明和红红坚持每天进行1分钟跳绳练习,并把连续7天的数据进行了记录,制成了下面的折线统计图。
(1)第四天两人的成绩相差( )个;第七天两人的成绩相差( )个。
(2)红红第( )天和第( )天跳的同样多。
(3)如果推荐两人中的一个人参加运动会的跳绳比赛,你推荐谁?说说你的理由。
8.明明和亮亮参加学校一分钟跳绳比赛,提前6天进行训练。每天测试成绩如下表:
(1)根据统计表中明明的数据,完成上面复式折线统计图。
(2)明明和亮亮跳绳个数相差最多的是第( )天,相差( )个。
(3)如果只派一名同学参加校级竞争赛,你想派谁去?并简要说明理由。
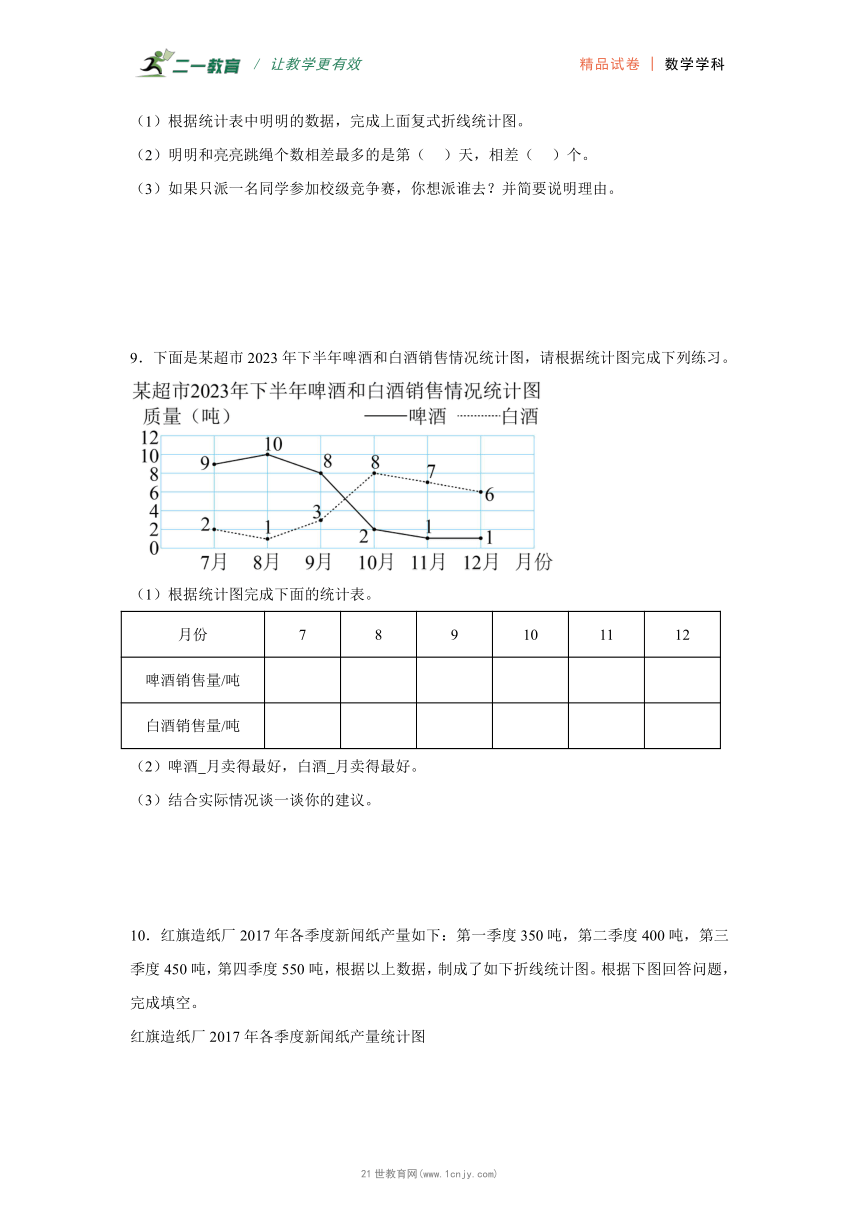
9.下面是某超市2023年下半年啤酒和白酒销售情况统计图,请根据统计图完成下列练习。
(1)根据统计图完成下面的统计表。
月份 7 8 9 10 11 12
啤酒销售量/吨
白酒销售量/吨
(2)啤酒 月卖得最好,白酒 月卖得最好。
(3)结合实际情况谈一谈你的建议。
10.红旗造纸厂2017年各季度新闻纸产量如下:第一季度350吨,第二季度400吨,第三季度450吨,第四季度550吨,根据以上数据,制成了如下折线统计图。根据下图回答问题,完成填空。
红旗造纸厂2017年各季度新闻纸产量统计图
(1)第( )季度的产量最高,是( )吨。
(2)四个季度的总产量是( )吨,平均每个季度的产量是( )吨。
(3)第( )季度到第( )季度的增长幅度最大。
11.欢欢和乐乐参加学校跳远训练,他们近五次跳远成绩如图。
跳远成绩统计图
(1)两人第二次跳远成绩相差( )厘米,第( )次相差最多。
(2)第三次乐乐的跳远成绩是欢欢的( )。
(3)欢欢训练中第( )次到第( )次上升的幅度最大。
(4)学校要派一名同学参加区里的跳远比赛,( )更加合适。说说你的理由。
12.根据统计图完成下列各题。
(1)在这五届冬季奥运会上,中国在冰上项目中共获得( )枚奖牌。
(2)冰上项目和雪上项目获得奖牌数量相差最多的是( )年冬季奥运会,相差( )枚。
(3)请结合图中的数据,预测下一届冬季奥运会中国冰上项目和雪上项目获得奖牌的情况,并简要说明理由。
13.科学课上,老师要求同学们完成一个植物种子发芽的观察实验。李明把一个水仙花球放在装满水的玻璃缸里,每隔一天观察一次,测量出芽和根的长度,并将结果绘制成了下面的统计图。
水仙花球根,芽生长情况统计图
(1)水仙花球第( )天开始生根,再过( )天开始发芽。
(2)第12天时芽的长度是根的。
(3)第( )天到第( )天时根和芽长得最快。
(4)从图中,你还能获取到哪些信息?
14.某城市旅游人数从2020年到2023年依次为200万、220万、280万、350万。
(1)完成如图统计图。
(2)从图中看出,从( )到( )年,游客人数增加最多。
(3)结合该城市旅游人数的变化情况,预估2024年该市游客人数将达( )万人。
(4)2024年游客人数发生这样变化的原因可能有哪些?请写出至少2条。
15.向阳小学五年级开展了以“知茶礼、懂茶道、学茶艺、传承茶艺文化”为主题的茶文化知识比赛。将五(1)班和五(2)班学生的比赛成绩绘制成如下所示的折线统计图。
(1)若成绩高于8分的为优秀,五(1)班比赛成绩优秀的人数有( )人,五(2)班比赛成绩优秀的人数有( )人。
(2)琪琪的成绩是五(1)班的第20名,她的成绩是( )分。
(3)从平均分来看,哪个班级对茶文化掌握得更好?
16.为倡导“低碳生活,绿色出行”,某市提倡市民实行“135”绿色出行方式,即1公里及以内步行,3公里及以内骑自行车,5公里左右乘坐公共交通。下面是该市2018~2023年公共汽车和地铁的客运量(单位:亿人次)情况统计表。
年份 2018 2019 2020 2021 2022 2023
公共汽车客运量 55 46 35 28 20 15
地铁客运量 16 20 25 30 32 35
(1)请根据表中的数据,画出折线统计图。
某市2018~2023年公共汽车和地铁的客运量情况统计图
(2)根据折线统计图填空。
①2018~2023年,公共汽车客运量整体呈( )趋势。(填“上升”或“下降”)
②2018~2023年,公共汽车和地铁的客运量相差最多的是( )年,相差了( )人次。
③小明看了上面的这些信息说:“越来越多的人选择地铁出行。”你同意他的说法吗?请简要说明理由。
17.下面是2023年上半年某汽车交易市场销售情况统计表。
月份 1 2 3 4 5 6
轿车/辆 300 250 220 170 200 230
货车/辆 100 150 90 100 100 140
(1)根据表中数据绘制折线统计图。
2023年上半年某汽车交易市场销售情况统计图
(2)两种车销售量相差最大的是( )月。
(3)2月份货车的销售量是轿车的。
(4)根据上面的数学信息,请你提出一个数学问题并解答。
18.奇思和妙想为了参加100米短跑比赛进行训练,下面是他们近10天的训练成绩统计图。
奇思和妙想近10天的训练成绩统计图
(1)奇思和妙想第( )天的成绩相差最大,相差( )秒。
(2)两人成绩呈现什么样的变化趋势?谁的进步幅度大些?
(3)你能预测两个人的比赛成绩吗?
19.共享单车是指企业在校园、商业区、公共服务区等提供自行车单车共享服务,是一种新型绿色环保共享经济,极大地方便了人们的出行.下面的折线统计图描述了小明去图书馆看书时的时间与路程之间的关系,步行到图书馆,然后骑支付宝单车返回,请根据折线统计图解答以下问题.www.21-cn-jy.com
(1)请写出折线统计图的特点.
(2)从折线统计图可以看出,小明家距离图书馆多少千米?小明在图书馆看书用多少小时(填带分数)?去时的步行速度是每小时多少千米?21*cnjy*com
(3)小明弟弟在小明出发20分钟后,步行去图书馆,然后在图书馆呆了30分钟,最后骑支付宝单车返回,去时速度、返回速度均与小明相同,请在图中画出相应的折线统计图.
20.星期天8:00~8:30,燃气公司给某加气站的储气罐注入天然气。在注入天然气之后,一位工作人员以每车20 立方米的加气量,依次给在加气站排队等候的若干辆车匀速加气。储气罐中的储气量y(立方米)与时间x(小时)的关系如图所示。21*cnjy*com
(1)8:00~8:30, 燃气公司向储气罐注入了多少立方米的天然气?
(2)请你判断:正在排队等候的第18 辆车能否在当天10:30 之前加完气? 请说明理由。
21.如图①,一个长方形纸条从正方形的左边开始以每秒2厘米的速度沿水平方向向右运动;如图②是运动过程中长方形纸条和正方形重叠部分的面积与运动时间的关系图。
(1)运动4秒后,重叠部分的面积是( )平方厘米。
(2)正方形的边长是( )厘米。
(3)在图②的括号内填入正确的时间。
22.一个长方体玻璃容器,底面积是800,高是1.05米。这个容器装有A、B两根进水管。先开A管,一段时间后两管同时开。
下图是该容器进水情况。看图回答问题。
(1)( )分钟后同时打开A、B两管,当时容器里的有( )升水。
(2)A、B两管同时进水,每分钟注入多少升水?
(3)如果继续注水,关掉B管单开A管,多少分钟后可将容器注满?请把图上的折线统计图接着面完整。
23.根据统计图完成下面各题。
(1)相邻的两年中,出生人口数增长最快的是从( )年到( )年,增长了( )万人。
(2)出生人口数和死亡人口数相差最多的是( )年,相差( )万人;出生人口数和死亡人口数相差最少的是( )年,相差( )万人。
(3)请你根据统计图中提供的信息,分析国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策?
(4)请你结合实际预测和分析未来五年我国出生人口数和死亡人口数的变化趋势。
24.如下左图,一个长为24厘米、宽为3厘米的长方形从正方形的左边平移到右边,下面右图是平移过程中它们重叠部分面积与时间的部分关系图。
(1)正方形的边长为___________厘米。
(2)当平移时间为多少秒时,长方形和正方形的重叠部分面积是30平方厘米?
25.王叔叔骑自行车匀速从甲地驶向乙地,在途中休息了一段时间后,仍按原速行驶,他离乙地的距离与时间的关系如图中折线所示。刘叔叔开车匀速从乙地驶向甲地,比王叔叔晚出发一段时间,他离乙地的距离与时间的关系如图中线段AB所示。王叔叔出发多少小时后与刘叔叔相距15千米?
《(核心素养应用意识)第七单元折线统计图(解决问二)-五年级数学下册人教版》参考答案
1.(1)2021年增长最快;5568元
(2)2022年的差距最大;34732元
(3)北京市居民人均可支配收入呈持续上升趋势,北京市居民人均消费支出整体呈上升趋势。
研究的数学问题:北京市居民人均可支配收入和人均消费支出相比,哪一年的差距最小。(答案不唯一)
【分析】(1)观察折线统计图,横线表示人均可支配收入,哪一年增长的横线倾斜最大,则增长的最快,增长的钱数=这一年的钱数-前一年的钱数。2·1·c·n·j·y
(2)观察折线统计图,横线和虚线之间差距最大是2022年,用2022年的人均支配收入减人均消费支出。
(3)折线统计图可以看出变化的趋势,人均可支配收入一直在上升。但是人均消费支出会上升会下降,但是整体是呈上升趋势的。继续研究的数学问题,答案不唯一,可以根据折线统计图的数据分析。
【详解】(1)75002-69434=5568(元)
答:北京市居民人均可支配收入2021年增长最快,增长了5568元。
(2)77415-42683=34732(元)
答:2022年差距最大,相差34732元。
(3)北京市居民人均可支配收入呈持续上升趋势,北京市居民人均消费支出整体呈上升趋势。
研究的数学问题:北京市居民人均可支配收入和人均消费支出相比,哪一年的差距最小。(答案不唯一)
2.(1)(2)见详解
(3)北海市;理由见详解
【分析】(1)折线向上表示呈上升趋势,折线向下表示呈下降趋势,据此解答即可;
(2)折线的斜度越大,则表示平均气温变化较大,反之表示平均气温变化较为平稳;
(3)若要选择居住的城市,应选择平均气温变化平稳的城市,据此解答即可。
【详解】(1)南充市2020年上半年月平均气温呈上升趋势。
(2)南充市2020年上半年平均气温变化较大,北海市2020年上半年平均气温变化较为平稳。
(3)我会选择北海市作为居住的城市,因为北海市的平均气温变化较为平稳。
3.(1)30;
(2)40;1.8;
(3)王老师;王老师距离终点更近,张老师的折线统计图的趋势比王老师的折线统计图趋势更平滑,则王老师的速度大于张老师的速度(理由答案不唯一)21·cn·jy·com
【分析】(1)观察折线统计图,实线是张老师,虚线是王老师,实线和虚线相差的距离最大,则两人相差的距离就最远。发现第30分钟的时候,两人的相差的距离最远。
(2)王老师一开始的速度比张老师的慢,在第40分钟的时候两人走的路程是一样的,就是第40分钟的时候王老师开始追上张老师。60分钟的时候张老师跑了7.1千米,王老师走了8.9千米,减法列式计算60分钟时王老师已经超过张老师多少千米。
(3)从统计图中可以看出王老师一直是上升的趋势,而张老师的速度反而出现了波动。王老师可以先到终点,理由合理即可;据此解答。21·世纪*教育网
【详解】(1)跑到30分钟时两人差距最远。
(2)8.9-7.1=1.8(千米)
所以王老师在40分钟时追上张老师,60分钟时王老师已经超过张老师1.8千米。
(3)答:王老师更有可能先到达终点,因为王老师距离终点更近,张老师的折线统计图的趋势比王老师的折线统计图趋势更平滑,则王老师的速度大于张老师的速度。(答案不唯一)
4.(1) 90 80
(2) 60 70
(3) 王明 刘强
【分析】(1)从统计图中可以直接看出,跑完全程,王明用了90秒,刘强用了80秒。
(2)找到路程300米所对应的时间,可知王明用了60秒,刘强用了70秒;
(3)通过观察统计图,前50秒,王明跑的路程比较远,因此可得王明跑得快些,第70-80秒,刘强的折线比较陡,路程增加比较明显,王明的折线比较缓,路程增加比较缓慢,因此第70-80秒,刘强跑得快些。
【详解】(1)跑完全程,王明用了90秒,刘强用了80秒。
(2)同样是跑300米,王明用了60秒,刘强用了70秒。
(3)前50秒,王明跑得快些,第70-80秒,刘强跑得快些。
5.(1)毛衣;衬衫
(2)上升;原因见详解
(3)见详解
【分析】(1)观察统计图,由于从夏天到冬天,气温越来越冷,衬衫的销量会减少,毛衣的销量会增加,据此找出图中“——”表示谁的销售情况,“…………”表示谁的销售情况;
(2)根据统计图,说出毛衣的销售变化,毛衣的销售变化是受天气原因;(原因不唯一)
(3)根据衬衣和毛衣销售量的变化,根据季节不同,来调整衬衣和毛衣的进货数量(答案不唯一)。
【详解】(1)图中“——”表示毛衣的销售情况,“…………”表示衬衫的销售情况。
(2)这半年毛衣的销售量呈上升变化趋势,引起这些变化的主要原因是下半年天气逐渐转凉,穿毛衣的人越来越多,穿衬衣的人越来越少。
(3)在夏天时,多进衬衣,冬天多进毛衣,衬衣少进。(答案不唯一)
6.(1)2015;2016;131
(2)2016;809;2021;48
(3)见详解
【分析】(1)相邻两年的出生人口增长最快,从统计图上只要找到折线倾斜角度最大的那段,据此解答;
(2)出生人口数和死亡人口数相差最多(最少),两条折线相距最远(最近),据此解答;
(3)实线、虚线的具体走势所代表的是出生人口与死亡人口的变化,据此解释国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策,据此解答。
【详解】(1)相邻的两年中,出生人口数增长最快的是从2015年到2016年,(万人),即增长了131万人。
(2)(万人),出生人口数和死亡人口数相差最多的是2016年,相差809万人;
(万人),出生人口数和死亡人口数相差最少的是2021年,相差48万人。
(3)从统计图可看出2015年之前人口增长过慢,而死亡人口数在不断增长,说明人口老龄化严重,子女赡养压力增大,所以提出“二胎”政策;而2015年提出“二胎”政策后,2016年出生人口数有所增长,但之后就持续减少,所以2021年又提出了“三孩”政策。(答案不唯一)
7.(1)4;2;
(2)五;六;
(3)红红;理由见详解
【分析】(1)观察复式折线统计图,分别找到第四天和第七天两人成绩,分别求差即可;
(2)观察复式折线统计图,实线表示红红成绩,数据点位置一样高表示,再对照数据即可;
(3)根据折线统计图的变化趋势进行分析,折线往上表示上升趋势,折线往下表示下降趋势,选成绩稳定上升的参加跳绳比赛,据此分析。
【详解】(1)162-158=4(个)、167-165=2(个)
第四天两人的成绩相差4个;第七天两人的成绩相差2个。
(2)红红第五天和第六天跳的同样多。
(3)推荐红红参加运动会的跳绳比赛,因为红红的成绩比较稳定,一直处于上升趋势。
8.(1)见详解;
(2)6;6;
(3)明明;因为他的成绩稳步上升(答案不唯一)
【分析】(1)将明明的成绩先描点,再用实线连接,完成复式折线统计图;
(2)两条折线距离最远时,两人的跳绳个数差距最多。所以,相差最多的是第6天,利用减法求出相差多少个;
(3)亮亮的成绩起伏不定,而明明的成绩稳步上升。所以,如果只派一名同学参加校级竞争赛,我会派明明去参赛。
【详解】
(1)如图:
(2)167-161=6(个)
所以,明明和亮亮跳绳个数相差最多的是第6天,相差6个。
(3)答:我会派明明去,因为他的成绩稳步上升。
9.(1)9;10;8;2;1;1
2;1;3;8;7;6
(2)8;10
(3)见详解
【分析】(1)根据复式折线统计图中的数据填写统计表即可。
(2)观察复式折线统计图,实线的最高点表示这个月啤酒卖得最好;虚线的最高点表示这个月白酒卖得最好。
(3)从复式折线统计图中获取信息,提出建议,合理即可。
【详解】(1)填表如下:
月份 7 8 9 10 11 12
啤酒销售量/吨 9 10 8 2 1 1
白酒销售量/吨 2 1 3 8 7 6
(2)啤酒8月卖得最好,白酒10月卖得最好。
(3)我的建议:7、8、9月份啤酒的销售量高,所以这三个月多进啤酒;10、11、12月份白酒的销售量高,所以这三个月多进白酒。(答案不唯一)21cnjy.com
10.(1) 四 550
(2) 1750 437.5
(3) 三 四
【分析】(1)折线统计图最高的部分是第几季度,第几季度的产量最高,写上相应的吨数即可;
(2)把四个季度的产量加起来就是四个季度的总产量,根据求平均数的方法,用四个季度的总产量除以4即可解答;
(3)第几季度到第几季度折线统计图的部分越陡,就是第几季度到第几季度的增长幅度最大。
【详解】(1)由折线统计图可知,第四季度的产量最高,是550吨;
(2)350+400+450+550
=750+450+550
=1200+550
=1750(吨)
1750÷4=437.5(吨)
所以四个季度的总产量是1750吨,平均每个季度的产量是437.5吨。
(3)由折线统计图可知,第三季度到第四季度的增长幅度最大。
11.(1)15;5
(2)
(3)2;3
(4)欢欢;欢欢的成绩稳步提升(答案不唯一)
【分析】(1)观察折线统计图,实线表示欢欢数据,虚线表示乐乐数据,找到第二次两人跳远成绩,求差;两数据点相距越远表示相差越多,据此分析;2-1-c-n-j-y
(2)将第三次欢欢的跳远成绩看作单位“1”,第三次乐乐的跳远成绩÷第三次欢欢的跳远成绩=第三次乐乐的跳远成绩是欢欢的几分之几;
(3)观察折线统计图,实线表示欢欢数据,折线往上坡度越陡表示上升幅度越大,据此分析;
(4)根据折线统计图的变化,折线往上表示上升趋势,折线往下表示下降趋势,派跳远成绩稳定且呈上升趋势的去参加跳远比赛。
【详解】(1)110-95=15(厘米)
两人第二次跳远成绩相差15厘米,第5次相差最多。
(2)95÷105==
第三次乐乐的跳远成绩是欢欢的。
(3)欢欢训练中第2次到第3次上升的幅度最大。
(4)学校要派一名同学参加区里的跳远比赛,欢欢更加合适。因为欢欢的成绩在稳步提升。(答案不唯一)
12.(1)35
(2)2006;7
(3)见详解
【分析】(1)在这五届冬季奥运会上,中国在冰上项目中获得的奖牌数量分别是9枚、8枚、7枚、5枚、6枚,把它们相加即可解答。
(2)观察折线统计图可知,2006年冰上项目获得奖牌9枚,雪上项目获得奖牌2枚,数量相差最多;9-2=7(枚),即相差7枚。
(3)从统计图中可以看出,在这五届冬季奥运会上,中国在冰上项目中获得的奖牌数量几乎逐届减少,而雪上项目获得的奖牌数量整体趋势是不断增加,据此可以预测:下一届冬季奥运会中国冰上项目获得的奖牌数量可能是5到7枚,雪上项目获得奖牌的数量还会增加。
【详解】(1)9+8+7+5+6=35(枚),则在这五届冬季奥运会上,中国在冰上项目中共获得35枚奖牌。
(2)9-2=7(枚),冰上项目和雪上项目获得奖牌数量相差最多的是2006年冬季奥运会,相差7枚。
(3)可以预测:下一届冬季奥运会中国冰上项目获得的奖牌数量可能是5到7枚,雪上项目获得奖牌的数量还会增加。因为在这五届冬季奥运会上,中国在冰上项目中获得的奖牌数量几乎逐届减少,而雪上项目获得的奖牌数量整体趋势是不断增加。(答案不唯一)
13.(1)4;4
(2)
(3)18;20
(4)第10天时芽的长度是根的几分之几?
【分析】(1)观察复式折线统计图,实线表示根的生长情况,虚线表示芽的生产情况,折线开始上升出表示开始生根和发芽,据此确定生根和发芽需要的天数,发芽需要的天数-生根需要的天数=生根后需要几天发芽;www-2-1-cnjy-com
(2)将第12天时根的长度看作单位“1”,第12天时芽的长度÷根的长度=第12天时芽的长度是根的几分之几;
(3)观察复式折线统计图,折线往上坡度越陡表示长得越快,据此分析;
(4)答案不唯一,合理即可,可以模仿第(2)小题提一个类似的问题。如第10天时芽的长度是根的几分之几?将第10天时根的长度看作单位“1”,第10天时芽的长度÷根的长度=第10天时芽的长度是根的几分之几。
【详解】(1)8-4=4(天)
水仙花球第4天开始生根,再过4天开始发芽。
(2)20÷52==
第12天时芽的长度是根的。
(3)第18天到第20天时根和芽长得最快。
(4)第10天时芽的长度是根的几分之几?
10÷40==
答:第10天时芽的长度是根的。
14.(1)图见详解;
(2)2022;2023;
(3)450;
(4)见详解
【详解】(1)将题目中的数据对应年份描点,然后将点和点依次连接起来。
(2)用减法求出相邻两年的数据差,再比较。
(3)根据折线统计图一直上升的局势,得出合理的数据即可。
(4)根据分析写出合理的原因。
【解答】(1)
(2)220-200=20(万人)
280-220=60(万人)
350-280=70(万人)
70>60>20
从图中看出,从2022到2023年,游客人数增加最多。
(3)结合该城市旅游人数的变化情况,预估2024年该市游客人数将达450万人(答案不唯一)。
(4)疫情过后旅游的人数由少逐渐变多;
人们更向往外面的世界。(答案不唯一)
15.(1)14;8
(2)8
(3)五(1)班
【分析】(1)观察复式折线统计图,实线表示五(1)班成绩,虚线表示五(2)班成绩,分别将两个班成绩高于8分的人数相加即可。21教育名师原创作品
(2)观察复式折线统计图,实线表示五(1)班成绩,10分有1人,是第1名,9分有13人,是前1+13=14(名),8分有10人,14+10=24(名),是第15名到第24名,据此分析。
(3)根据平均数=总数÷份数,分别计算出两个班的平均分,比较即可。
【详解】(1)13+1=14(人)、6+2=8(人)
若成绩高于8分的为优秀,五(1)班比赛成绩优秀的人数有14人,五(2)班比赛成绩优秀的人数有8人。
(2)1+13=14(名)、14+10=24(名)
第15名到第24名都是8分,琪琪的成绩是五(1)班的第20名,她的成绩是8分。
(3)五(1)班的平均分:(9×6+7×7+10×8+13×9+1×10)÷(9+7+10+13+1)
=(54+49+80+117+10)÷40
=310÷40
=7.75(分)
五(2)班的平均分:(11×6+12×7+9×8+6×9+2×10)÷(11+12+9+6+2)
=(66+84+72+54+20)÷40
=296÷40
=7.4(分)
7.75>7.4
答:从平均分来看,五(1)班对茶文化掌握得更好。
16.(1)见详解
(2)①下降
②2018;39亿
③同意;理由见详解
【分析】(1)实线表示公共汽车数据,虚线表示地铁数据;根据各数量的多少,在方格图的纵、横的交点上描出表示数量多少的点;把各点用线段顺次连接起来。
(2)①实线表示公共汽车数据,折线往上表示上升趋势,折线往下表示下降趋势,据此填空;
②同一年份,两数据点相距越远表示客运量相差越多,据此确定客运量相差最多的年份,再求出这一年公共汽车和地铁客运量的差即可。【版权所有:21教育】
③根据折线统计图折线上升和下降的变化趋势进行分析,折线往上表示上升趋势,说明人数越来越多,据此解答。
【详解】(1)某市2018~2023年公共汽车和地铁的客运量情况统计图
(2)①2018~2023年,公共汽车客运量整体呈下降趋势。
②55-16=39(亿人)
2018~2023年,公共汽车和地铁的客运量相差最多的是2018年,相差了39亿人次。
③同意他的说法,因为选择地铁出行的人数呈上升趋势,选择公共汽车出行的人数呈下降趋势,从2021年开始已经超过选择公共汽车出行的人数。(理由答案不唯一)
17.(1)见详解
(2)1
(3)
(4)5月份货车的销售量是轿车的几分之几?(答案不唯一)
【分析】(1)先确定图例,用实线表示轿车的销售情况,用虚线表示货车的销售情况;再结合统计表中数据的大小,分别描出两组数据的各点,并根据图例把各点用线段顺次连接起来,完成复式折线统计图的绘制。
(2)观察复式折线统计图,两条折线的叉口最大时,表示这个月两种车销售量相差最大。
(3)从图中可知,2月份轿车销售250辆,货车销售150辆,用货车的销售量除以轿车的销售量,即是2月份货车的销售量是轿车的几分之几。
(4)结合复式折线统计图提供的信息,提出问题,并解答,合理即可。
如提问:5月份货车的销售量是轿车的几分之几?
用5月份货车的销售量除以轿车的销售量即可。
【详解】(1)如图:
(2)两种车销售量相差最大的是1月。
(3)150÷250=
2月份货车的销售量是轿车的。
(4)提问:5月份货车的销售量是轿车的几分之几?(答案不唯一)
100÷200=
答:5月份货车的销售量是轿车的。
18.(1)5;3
(2)(3)见详解
【分析】(1)通过观察统计图可知,奇思和妙想第5天的成绩相差最大,根据求一个数比另一个数多或少几,用减法解答;
(2)观察折线统计图的走向,所用时间越少,说明进步越大;据此判断两人成绩呈现上升或下降的变化趋势,再进一步观察谁的进步幅度大些。
(3)比赛的时候,奇思的成绩可能比妙想的好,可以预测奇思的比赛成绩和妙想的比赛成绩。
【详解】(1)24-21=3(秒)
奇思和妙想第5天的成绩相差最大,相差3秒。
(2)两人成绩呈现上升的变化趋势,奇思的进步幅度大些。
(3)可以预测奇思的比赛成绩可能是17秒,妙想的比赛成绩可能是18秒。(答案不唯一)
19.(1)不仅可以表示数量的多少,而且可以反映数据的增减变化情况.
(2)4km,小时,8千米/时
(3)
【详解】(1)不仅可以表示数量的多少,而且可以反映数据的增减变化情况.
(2)小明家距离图书馆4千米
由统计图的水平线的起止时间相减即可得到在图书馆看书的时间
100﹣30=70(分钟)=(小时)
运用路程4千米除以时间(30分钟=0.5小时)等于速度即可进行计算.
4÷(30÷60)=8(千米/时)
(3)
20.(1)8000立方米
(2)能在当天10:30之前加完气;详解见解析
【分析】整个过程相当于储气罐里的天然气先增加,后减少,起始时刻,储气罐里的天然气是原来就要的,最高的是燃气公司给储气罐注入天然气结束时的数量;根据天然气的减少的速度,可以求出给每辆车加气需要的时间,然后求出给所有车加完气需要的时间,进行比较。
【详解】(1)(立方米)
答:燃气公司向储气罐注入了8000立方米的天然气。
(2)8点半开始加气,从10000立方米下降到8000立方米,下降了2000立方米,使用时间是10小时,可以求出加气的速度;
(立方米)
每小时加气200立方米,8点半距离10点半有2小时;
(立方米)
(辆)
10点半之前可供20辆车加气完成,所以第18辆车可以在当天10:30之前加完气。
【点睛】本题是将折线统计图与实际问题相结合,首先要充分理解统计图所表示的含义,然后再求解问题。
21.(1)16
(2)12
(3)
【分析】在表示路程和时间的行程问题的折线统计图中,折线上升,表示向目的地运动;折线呈水平方向,表示在某地停留,折线下降,表示向出发地运动。据此可解答。
(1)运动4秒,运动的长是2×4=8(厘米),宽是2厘米,重叠部分的面积是长方形8×2=16(平方厘米),据此可解答。
(2)根据题意看图,第6秒以后,重叠部分开始不变,即正方形的边长是6×2=12(厘米),据此解答即可。
(3)当长方形的左端,刚好穿过正方形时,还需要8+2=10(秒)。所以第一个括号填10。
长方形的左端完全离开正方形,相当于火车行程问题,(20+12) +2=16(秒)
所以第二个括号填16,没有重叠部分,面积为0。
【详解】(1)8×2=16(平方厘米)
(2)6×2=12(厘米)
(3)
【点睛】这里有行程问题,折线统计图问题,通过折线统计图分析长方形纸条和正方形重叠部分的面积与运动时间是解题的关键。
22.(1)10;24
(2)3.6升
(3)10分钟;作图见详解
【分析】(1)观察统计图,折线往上坡度变陡,说明同时打开了两根进水管;根据长方体体积=底面积×高,求出水的体积即可。
(2)求出10至20分钟的注水量,除以分钟数即可。
(3)先求出容器剩余容积,除以A管每分钟注水量就是继续注水将容器注满的时间,补充统计图即可。
【详解】(1)800×30=24000(立方厘米)=24(升)
10分钟后同时打开A、B两管,当时容器里的有24升水。
(2)800×(75-30)÷(20-10)
=800×45÷10
=3600(立方厘米)=3.6(升)
答:每分钟注入3.6升水。
(3)800×(105-75)
=800×30
=24000(立方厘米)=24(升)
24÷(24÷10)
=24÷2.4
=10(分钟)
答:10分钟后可将容器注满。
【点睛】关键是掌握长方体体积公式,折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
23.(1)2015;2016;131;
(2)2016;809;2021;48;
(3)(4)见详解
【分析】(1)结合统计图可知,出生人口呈增长趋势的是从2011年到2016年,其中,折线坡度最陡的一段,就表示相邻的这两年中,出生人口增长最快;这两年是从2015年到2016年;再用靠后年份对应的出生人口数减去靠前年份对应的出生人口数,得到具体增长了几万人;
(2)折线统计图中,表示同一年度出生人数和死亡人数的两个点距离越长,两数相差越大,从图上看出出生和死亡人数相差较大的是2016年和2017年;分别求得这两年出生人口数和死亡人口数的差,比较大小,较大的就是所求;【来源:21cnj*y.co*m】
同理:表示同一年度出生人数和死亡人数的两个点距离越短,两数相差越小,从图上看出是2021年,把这两年的人口数作差,就是所求;
(3)可结合统计图中,实线虚线的具体走势所代表的出生人口与死亡人口的变化,来解释国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策;
(4)可结合“三孩”政策提出可能产生的效果,以及统计图中虚线较缓的走势来分析预测。
【详解】(1)1786-1655=131(万人)
相邻的两年中,出生人口数增长最快的是从(2015)年到(2016)年,增长了(131)万人。
(2)2016年相差:1786-977=809(万人)
2017年相差:1723-986=737(万人)
809>737,所以2016年出生人口数与死亡人口数相差最多。
2021年相差:1062-1014=48(万人)
出生人口数和死亡人口数相差最多的是(2016)年,相差(809)万人;出生人口数和死亡人口数相差最少的是(2021)年,相差(48)万人。【来源:21·世纪·教育·网】
(3)从统计图可看出2015年之前人口增长过慢,而死亡人口数在不断增长,说明人口老龄化严重,子女赡养压力增大,所以提出“二胎”政策;
而2015年提出“二胎”政策后,2016年出生人口数有所增长,但之后就持续减少,所以2021年又提出了“三孩”政策。
(4)预测未来五年我国出生人口数将有所增长,因为2021年提出了“三孩”政策。按照统计图中的变化趋势,未来五年我国死亡人口数也将成缓慢增长趋势。
【点睛】本题较为复杂,结合统计图分析现状,需要仔细读图和大量计算;结合实际来预测需要学生充分理解题意并展开想象。
24.(1)12;
(2)5秒或13秒
【分析】(1)由重叠面积与时间的关系图知,长方形每秒移12÷2÷3=2(厘米),当从第6秒开始,重叠面积没发生变化,说明长方形的右边宽的部分已经移到正方形的右边,此时移动:2×6=12(厘米),所以正方形边长为12厘米;
(2)当长方形从正方形左边移到右边时,会有两个时刻与正方形的重叠面积是30平方厘米,第一个时刻是长方形刚移到正方形内时,此时长方形的右半部分与正方形重叠,此时移动(30÷3=10)厘米,用(10÷ 2=5秒);第二个时刻是长方形从正方形内移出时,此时长方形只剩左半部分与正方形重叠,还有(30÷3=10)厘米在正方形内,共移[24+(12-10)=26]厘米,用(26÷2=13)秒。
【详解】(1)12 ÷2÷3
=6÷3
=2(厘米)
长方形每秒移动2厘米,正方形的边长是运行6秒后的长度:
2×6=12(厘米)
所以,正方形的边长为12厘米。
(2)正方形的重叠面积是30平方厘米,
30÷3=10(厘米)
10÷2=5(秒)
第一个时刻是长方形刚移到正方形内时,此时长方形的右半部分与正方形重叠,此时移动了10厘米,用了5秒;21教育网
30÷3=10(厘米)
24+2=26(厘米)
26÷2=13(秒)
第二个时刻是长方形从正方形内移出时,此时长方形只剩左半部分与正方形重叠,还有10厘米在正方形内,共移动了26厘米,用了13秒。
答:当平移时间为5秒或13秒时,长方形和正方形的重叠部分面积是30平方厘米。
【点睛】此题考查了匀速运动这一知识,以及分析折线统计图的能力。
25.6.4小时或6.8小时
【分析】从图中可知,甲、乙两地的距离是120千米;王叔叔骑车从甲地到乙地中间休息了1小时,到达目的地用时(9-1)小时;刘叔叔开车从乙地到甲地用时(8-6)小时;根据“速度=路程÷时间”,分别求王叔叔骑车的速度和刘叔叔开车的速度。
当刘叔叔出发时,王叔叔骑车已行了(6-1)小时,根据“路程=速度×时间”求出王叔叔先行的路程;再用全程减去王叔叔先行的路程,即是当刘叔叔出发时两人相距的距离。
求王叔叔出发多少小时后与刘叔叔相距15千米,分两种情况:
情况一:两人相遇前相距15千米时,用刘叔叔出发时两人相距的距离减去15,即是两人相遇前行的路程之和,再除以两人的速度和,求出两人相距15千米时行的时间,最后加上王叔叔早出发的6小时即可;
情况二:两人相遇后相距15千米时,用刘叔叔出发时两人相距的距离加上15,即是两人相遇前行的路程之和,再除以两人的速度和,求出两人相距15千米时行的时间,最后加上王叔叔早出发的6小时即可。
【详解】刘叔叔开车的速度:
120÷(8-6)
=120÷2
=60(千米/时)
王叔叔骑车的速度:
120÷(9-1)
=120÷8
=15(千米/时)
当刘叔叔出发时,两人相距:
120-15×(6-1)
=120-15×5
=120-75
=45(千米)
情况一:两人相遇前相距15千米
(45-15)÷(60+15)
=30÷75
=0.4(小时)
6+0.4=6.4(小时)
情况二:两人相遇后相距15千米
(45+15)÷(60+15)
=60÷75
=0.8(小时)
6+0.8=6.8(小时)
答:王叔叔出发6.4小时或6.8小时后与刘叔叔相距15千米。
【点睛】先从时间与距离的关系图中获取信息,根据速度、时间、路程之间的关系分别求出两人的速度以及刘叔叔出发时两人相距的距离;然后分两种情况讨论两人何时相距15千米是解题的关键。【出处:21教育名师】
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
第七单元折线统计图
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.观察统计图,回答问题。
北京市2018-2022年居民人均可支配收入和人均消费支出统计图
(1)北京市居民人均可支配收入哪一年增长最快?增长了多少元?
(2)北京市居民人均可支配收入和人均消费支出相比,哪一年的差距最大?相差了多少元?
(3)北京市居民人均可支配收入和人均消费支出呈现怎样的变化趋势?通过这些数据,请你提出一个想继续研究的数学问题。
2.下面是北海、南充两个市2020年上半年月平均气温变化情况统计图,请你回答下面问题。
(1)南充市2020年上半年月平均气温是怎样变化的?
(2)南充市和北海市2020年上半年平均气温变化情况有什么区别?
(3)如果让你选择居住的城市,你选择哪座城市,为什么?
3.今年柳州举行了马拉松比赛,张老师、王老师参加了10千米的“健康跑”。比赛到60分钟时两位老师跑步的情况如图所示。
(1)跑到( )分钟时两人差距最远。
(2)王老师在( )分钟时追上张老师,60分钟时王老师已经超过张老师( )千米。
(3)他们两人谁更有可能先到达终点?请说明理由。
4.看统计图完成后面的填空。
王明和刘强400米赛跑情况的折线统计图
(1)跑完全程,王明用了( )秒,刘强用了( )秒。
(2)同样是跑300米,王明用了( )秒,刘强用了( )秒。
(3)前50秒,( )跑得快些,第70-80秒,( )跑得快些。
5.下图是去年下半年某商场毛衣和衬衫的销售情况统计图。
商场毛衣、衬衫销售情况统计图
仔细观察统计图,完成下列问题。
(1)图中“——”表示( )的销售情况,“…………”表示( )的销售情况。
(2)这半年毛衣的销售量呈( )变化趋势,你认为引起这些变化的主要原因是( )。
(3)如果你是销售经理,在进货方面有什么考虑?
6.根据统计图完成下面各题。
2011年~2021年全国出生人口数和死亡人口数统计图
(1)相邻的两年中,出生人口数增长最快的是从( )年到( )年,增长了( )万人。
(2)出生人口数和死亡人口数相差最多的是( )年,相差( )万人;出生人口数和死亡人口数相差最少的是( )年,相差( )万人。21世纪教育网版权所有
(3)请你根据统计图中提供的信息,分析国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策?
7.为了获得运动会跳绳比赛资格,明明和红红坚持每天进行1分钟跳绳练习,并把连续7天的数据进行了记录,制成了下面的折线统计图。
(1)第四天两人的成绩相差( )个;第七天两人的成绩相差( )个。
(2)红红第( )天和第( )天跳的同样多。
(3)如果推荐两人中的一个人参加运动会的跳绳比赛,你推荐谁?说说你的理由。
8.明明和亮亮参加学校一分钟跳绳比赛,提前6天进行训练。每天测试成绩如下表:
(1)根据统计表中明明的数据,完成上面复式折线统计图。
(2)明明和亮亮跳绳个数相差最多的是第( )天,相差( )个。
(3)如果只派一名同学参加校级竞争赛,你想派谁去?并简要说明理由。
9.下面是某超市2023年下半年啤酒和白酒销售情况统计图,请根据统计图完成下列练习。
(1)根据统计图完成下面的统计表。
月份 7 8 9 10 11 12
啤酒销售量/吨
白酒销售量/吨
(2)啤酒 月卖得最好,白酒 月卖得最好。
(3)结合实际情况谈一谈你的建议。
10.红旗造纸厂2017年各季度新闻纸产量如下:第一季度350吨,第二季度400吨,第三季度450吨,第四季度550吨,根据以上数据,制成了如下折线统计图。根据下图回答问题,完成填空。
红旗造纸厂2017年各季度新闻纸产量统计图
(1)第( )季度的产量最高,是( )吨。
(2)四个季度的总产量是( )吨,平均每个季度的产量是( )吨。
(3)第( )季度到第( )季度的增长幅度最大。
11.欢欢和乐乐参加学校跳远训练,他们近五次跳远成绩如图。
跳远成绩统计图
(1)两人第二次跳远成绩相差( )厘米,第( )次相差最多。
(2)第三次乐乐的跳远成绩是欢欢的( )。
(3)欢欢训练中第( )次到第( )次上升的幅度最大。
(4)学校要派一名同学参加区里的跳远比赛,( )更加合适。说说你的理由。
12.根据统计图完成下列各题。
(1)在这五届冬季奥运会上,中国在冰上项目中共获得( )枚奖牌。
(2)冰上项目和雪上项目获得奖牌数量相差最多的是( )年冬季奥运会,相差( )枚。
(3)请结合图中的数据,预测下一届冬季奥运会中国冰上项目和雪上项目获得奖牌的情况,并简要说明理由。
13.科学课上,老师要求同学们完成一个植物种子发芽的观察实验。李明把一个水仙花球放在装满水的玻璃缸里,每隔一天观察一次,测量出芽和根的长度,并将结果绘制成了下面的统计图。
水仙花球根,芽生长情况统计图
(1)水仙花球第( )天开始生根,再过( )天开始发芽。
(2)第12天时芽的长度是根的。
(3)第( )天到第( )天时根和芽长得最快。
(4)从图中,你还能获取到哪些信息?
14.某城市旅游人数从2020年到2023年依次为200万、220万、280万、350万。
(1)完成如图统计图。
(2)从图中看出,从( )到( )年,游客人数增加最多。
(3)结合该城市旅游人数的变化情况,预估2024年该市游客人数将达( )万人。
(4)2024年游客人数发生这样变化的原因可能有哪些?请写出至少2条。
15.向阳小学五年级开展了以“知茶礼、懂茶道、学茶艺、传承茶艺文化”为主题的茶文化知识比赛。将五(1)班和五(2)班学生的比赛成绩绘制成如下所示的折线统计图。
(1)若成绩高于8分的为优秀,五(1)班比赛成绩优秀的人数有( )人,五(2)班比赛成绩优秀的人数有( )人。
(2)琪琪的成绩是五(1)班的第20名,她的成绩是( )分。
(3)从平均分来看,哪个班级对茶文化掌握得更好?
16.为倡导“低碳生活,绿色出行”,某市提倡市民实行“135”绿色出行方式,即1公里及以内步行,3公里及以内骑自行车,5公里左右乘坐公共交通。下面是该市2018~2023年公共汽车和地铁的客运量(单位:亿人次)情况统计表。
年份 2018 2019 2020 2021 2022 2023
公共汽车客运量 55 46 35 28 20 15
地铁客运量 16 20 25 30 32 35
(1)请根据表中的数据,画出折线统计图。
某市2018~2023年公共汽车和地铁的客运量情况统计图
(2)根据折线统计图填空。
①2018~2023年,公共汽车客运量整体呈( )趋势。(填“上升”或“下降”)
②2018~2023年,公共汽车和地铁的客运量相差最多的是( )年,相差了( )人次。
③小明看了上面的这些信息说:“越来越多的人选择地铁出行。”你同意他的说法吗?请简要说明理由。
17.下面是2023年上半年某汽车交易市场销售情况统计表。
月份 1 2 3 4 5 6
轿车/辆 300 250 220 170 200 230
货车/辆 100 150 90 100 100 140
(1)根据表中数据绘制折线统计图。
2023年上半年某汽车交易市场销售情况统计图
(2)两种车销售量相差最大的是( )月。
(3)2月份货车的销售量是轿车的。
(4)根据上面的数学信息,请你提出一个数学问题并解答。
18.奇思和妙想为了参加100米短跑比赛进行训练,下面是他们近10天的训练成绩统计图。
奇思和妙想近10天的训练成绩统计图
(1)奇思和妙想第( )天的成绩相差最大,相差( )秒。
(2)两人成绩呈现什么样的变化趋势?谁的进步幅度大些?
(3)你能预测两个人的比赛成绩吗?
19.共享单车是指企业在校园、商业区、公共服务区等提供自行车单车共享服务,是一种新型绿色环保共享经济,极大地方便了人们的出行.下面的折线统计图描述了小明去图书馆看书时的时间与路程之间的关系,步行到图书馆,然后骑支付宝单车返回,请根据折线统计图解答以下问题.www.21-cn-jy.com
(1)请写出折线统计图的特点.
(2)从折线统计图可以看出,小明家距离图书馆多少千米?小明在图书馆看书用多少小时(填带分数)?去时的步行速度是每小时多少千米?21*cnjy*com
(3)小明弟弟在小明出发20分钟后,步行去图书馆,然后在图书馆呆了30分钟,最后骑支付宝单车返回,去时速度、返回速度均与小明相同,请在图中画出相应的折线统计图.
20.星期天8:00~8:30,燃气公司给某加气站的储气罐注入天然气。在注入天然气之后,一位工作人员以每车20 立方米的加气量,依次给在加气站排队等候的若干辆车匀速加气。储气罐中的储气量y(立方米)与时间x(小时)的关系如图所示。21*cnjy*com
(1)8:00~8:30, 燃气公司向储气罐注入了多少立方米的天然气?
(2)请你判断:正在排队等候的第18 辆车能否在当天10:30 之前加完气? 请说明理由。
21.如图①,一个长方形纸条从正方形的左边开始以每秒2厘米的速度沿水平方向向右运动;如图②是运动过程中长方形纸条和正方形重叠部分的面积与运动时间的关系图。
(1)运动4秒后,重叠部分的面积是( )平方厘米。
(2)正方形的边长是( )厘米。
(3)在图②的括号内填入正确的时间。
22.一个长方体玻璃容器,底面积是800,高是1.05米。这个容器装有A、B两根进水管。先开A管,一段时间后两管同时开。
下图是该容器进水情况。看图回答问题。
(1)( )分钟后同时打开A、B两管,当时容器里的有( )升水。
(2)A、B两管同时进水,每分钟注入多少升水?
(3)如果继续注水,关掉B管单开A管,多少分钟后可将容器注满?请把图上的折线统计图接着面完整。
23.根据统计图完成下面各题。
(1)相邻的两年中,出生人口数增长最快的是从( )年到( )年,增长了( )万人。
(2)出生人口数和死亡人口数相差最多的是( )年,相差( )万人;出生人口数和死亡人口数相差最少的是( )年,相差( )万人。
(3)请你根据统计图中提供的信息,分析国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策?
(4)请你结合实际预测和分析未来五年我国出生人口数和死亡人口数的变化趋势。
24.如下左图,一个长为24厘米、宽为3厘米的长方形从正方形的左边平移到右边,下面右图是平移过程中它们重叠部分面积与时间的部分关系图。
(1)正方形的边长为___________厘米。
(2)当平移时间为多少秒时,长方形和正方形的重叠部分面积是30平方厘米?
25.王叔叔骑自行车匀速从甲地驶向乙地,在途中休息了一段时间后,仍按原速行驶,他离乙地的距离与时间的关系如图中折线所示。刘叔叔开车匀速从乙地驶向甲地,比王叔叔晚出发一段时间,他离乙地的距离与时间的关系如图中线段AB所示。王叔叔出发多少小时后与刘叔叔相距15千米?
《(核心素养应用意识)第七单元折线统计图(解决问二)-五年级数学下册人教版》参考答案
1.(1)2021年增长最快;5568元
(2)2022年的差距最大;34732元
(3)北京市居民人均可支配收入呈持续上升趋势,北京市居民人均消费支出整体呈上升趋势。
研究的数学问题:北京市居民人均可支配收入和人均消费支出相比,哪一年的差距最小。(答案不唯一)
【分析】(1)观察折线统计图,横线表示人均可支配收入,哪一年增长的横线倾斜最大,则增长的最快,增长的钱数=这一年的钱数-前一年的钱数。2·1·c·n·j·y
(2)观察折线统计图,横线和虚线之间差距最大是2022年,用2022年的人均支配收入减人均消费支出。
(3)折线统计图可以看出变化的趋势,人均可支配收入一直在上升。但是人均消费支出会上升会下降,但是整体是呈上升趋势的。继续研究的数学问题,答案不唯一,可以根据折线统计图的数据分析。
【详解】(1)75002-69434=5568(元)
答:北京市居民人均可支配收入2021年增长最快,增长了5568元。
(2)77415-42683=34732(元)
答:2022年差距最大,相差34732元。
(3)北京市居民人均可支配收入呈持续上升趋势,北京市居民人均消费支出整体呈上升趋势。
研究的数学问题:北京市居民人均可支配收入和人均消费支出相比,哪一年的差距最小。(答案不唯一)
2.(1)(2)见详解
(3)北海市;理由见详解
【分析】(1)折线向上表示呈上升趋势,折线向下表示呈下降趋势,据此解答即可;
(2)折线的斜度越大,则表示平均气温变化较大,反之表示平均气温变化较为平稳;
(3)若要选择居住的城市,应选择平均气温变化平稳的城市,据此解答即可。
【详解】(1)南充市2020年上半年月平均气温呈上升趋势。
(2)南充市2020年上半年平均气温变化较大,北海市2020年上半年平均气温变化较为平稳。
(3)我会选择北海市作为居住的城市,因为北海市的平均气温变化较为平稳。
3.(1)30;
(2)40;1.8;
(3)王老师;王老师距离终点更近,张老师的折线统计图的趋势比王老师的折线统计图趋势更平滑,则王老师的速度大于张老师的速度(理由答案不唯一)21·cn·jy·com
【分析】(1)观察折线统计图,实线是张老师,虚线是王老师,实线和虚线相差的距离最大,则两人相差的距离就最远。发现第30分钟的时候,两人的相差的距离最远。
(2)王老师一开始的速度比张老师的慢,在第40分钟的时候两人走的路程是一样的,就是第40分钟的时候王老师开始追上张老师。60分钟的时候张老师跑了7.1千米,王老师走了8.9千米,减法列式计算60分钟时王老师已经超过张老师多少千米。
(3)从统计图中可以看出王老师一直是上升的趋势,而张老师的速度反而出现了波动。王老师可以先到终点,理由合理即可;据此解答。21·世纪*教育网
【详解】(1)跑到30分钟时两人差距最远。
(2)8.9-7.1=1.8(千米)
所以王老师在40分钟时追上张老师,60分钟时王老师已经超过张老师1.8千米。
(3)答:王老师更有可能先到达终点,因为王老师距离终点更近,张老师的折线统计图的趋势比王老师的折线统计图趋势更平滑,则王老师的速度大于张老师的速度。(答案不唯一)
4.(1) 90 80
(2) 60 70
(3) 王明 刘强
【分析】(1)从统计图中可以直接看出,跑完全程,王明用了90秒,刘强用了80秒。
(2)找到路程300米所对应的时间,可知王明用了60秒,刘强用了70秒;
(3)通过观察统计图,前50秒,王明跑的路程比较远,因此可得王明跑得快些,第70-80秒,刘强的折线比较陡,路程增加比较明显,王明的折线比较缓,路程增加比较缓慢,因此第70-80秒,刘强跑得快些。
【详解】(1)跑完全程,王明用了90秒,刘强用了80秒。
(2)同样是跑300米,王明用了60秒,刘强用了70秒。
(3)前50秒,王明跑得快些,第70-80秒,刘强跑得快些。
5.(1)毛衣;衬衫
(2)上升;原因见详解
(3)见详解
【分析】(1)观察统计图,由于从夏天到冬天,气温越来越冷,衬衫的销量会减少,毛衣的销量会增加,据此找出图中“——”表示谁的销售情况,“…………”表示谁的销售情况;
(2)根据统计图,说出毛衣的销售变化,毛衣的销售变化是受天气原因;(原因不唯一)
(3)根据衬衣和毛衣销售量的变化,根据季节不同,来调整衬衣和毛衣的进货数量(答案不唯一)。
【详解】(1)图中“——”表示毛衣的销售情况,“…………”表示衬衫的销售情况。
(2)这半年毛衣的销售量呈上升变化趋势,引起这些变化的主要原因是下半年天气逐渐转凉,穿毛衣的人越来越多,穿衬衣的人越来越少。
(3)在夏天时,多进衬衣,冬天多进毛衣,衬衣少进。(答案不唯一)
6.(1)2015;2016;131
(2)2016;809;2021;48
(3)见详解
【分析】(1)相邻两年的出生人口增长最快,从统计图上只要找到折线倾斜角度最大的那段,据此解答;
(2)出生人口数和死亡人口数相差最多(最少),两条折线相距最远(最近),据此解答;
(3)实线、虚线的具体走势所代表的是出生人口与死亡人口的变化,据此解释国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策,据此解答。
【详解】(1)相邻的两年中,出生人口数增长最快的是从2015年到2016年,(万人),即增长了131万人。
(2)(万人),出生人口数和死亡人口数相差最多的是2016年,相差809万人;
(万人),出生人口数和死亡人口数相差最少的是2021年,相差48万人。
(3)从统计图可看出2015年之前人口增长过慢,而死亡人口数在不断增长,说明人口老龄化严重,子女赡养压力增大,所以提出“二胎”政策;而2015年提出“二胎”政策后,2016年出生人口数有所增长,但之后就持续减少,所以2021年又提出了“三孩”政策。(答案不唯一)
7.(1)4;2;
(2)五;六;
(3)红红;理由见详解
【分析】(1)观察复式折线统计图,分别找到第四天和第七天两人成绩,分别求差即可;
(2)观察复式折线统计图,实线表示红红成绩,数据点位置一样高表示,再对照数据即可;
(3)根据折线统计图的变化趋势进行分析,折线往上表示上升趋势,折线往下表示下降趋势,选成绩稳定上升的参加跳绳比赛,据此分析。
【详解】(1)162-158=4(个)、167-165=2(个)
第四天两人的成绩相差4个;第七天两人的成绩相差2个。
(2)红红第五天和第六天跳的同样多。
(3)推荐红红参加运动会的跳绳比赛,因为红红的成绩比较稳定,一直处于上升趋势。
8.(1)见详解;
(2)6;6;
(3)明明;因为他的成绩稳步上升(答案不唯一)
【分析】(1)将明明的成绩先描点,再用实线连接,完成复式折线统计图;
(2)两条折线距离最远时,两人的跳绳个数差距最多。所以,相差最多的是第6天,利用减法求出相差多少个;
(3)亮亮的成绩起伏不定,而明明的成绩稳步上升。所以,如果只派一名同学参加校级竞争赛,我会派明明去参赛。
【详解】
(1)如图:
(2)167-161=6(个)
所以,明明和亮亮跳绳个数相差最多的是第6天,相差6个。
(3)答:我会派明明去,因为他的成绩稳步上升。
9.(1)9;10;8;2;1;1
2;1;3;8;7;6
(2)8;10
(3)见详解
【分析】(1)根据复式折线统计图中的数据填写统计表即可。
(2)观察复式折线统计图,实线的最高点表示这个月啤酒卖得最好;虚线的最高点表示这个月白酒卖得最好。
(3)从复式折线统计图中获取信息,提出建议,合理即可。
【详解】(1)填表如下:
月份 7 8 9 10 11 12
啤酒销售量/吨 9 10 8 2 1 1
白酒销售量/吨 2 1 3 8 7 6
(2)啤酒8月卖得最好,白酒10月卖得最好。
(3)我的建议:7、8、9月份啤酒的销售量高,所以这三个月多进啤酒;10、11、12月份白酒的销售量高,所以这三个月多进白酒。(答案不唯一)21cnjy.com
10.(1) 四 550
(2) 1750 437.5
(3) 三 四
【分析】(1)折线统计图最高的部分是第几季度,第几季度的产量最高,写上相应的吨数即可;
(2)把四个季度的产量加起来就是四个季度的总产量,根据求平均数的方法,用四个季度的总产量除以4即可解答;
(3)第几季度到第几季度折线统计图的部分越陡,就是第几季度到第几季度的增长幅度最大。
【详解】(1)由折线统计图可知,第四季度的产量最高,是550吨;
(2)350+400+450+550
=750+450+550
=1200+550
=1750(吨)
1750÷4=437.5(吨)
所以四个季度的总产量是1750吨,平均每个季度的产量是437.5吨。
(3)由折线统计图可知,第三季度到第四季度的增长幅度最大。
11.(1)15;5
(2)
(3)2;3
(4)欢欢;欢欢的成绩稳步提升(答案不唯一)
【分析】(1)观察折线统计图,实线表示欢欢数据,虚线表示乐乐数据,找到第二次两人跳远成绩,求差;两数据点相距越远表示相差越多,据此分析;2-1-c-n-j-y
(2)将第三次欢欢的跳远成绩看作单位“1”,第三次乐乐的跳远成绩÷第三次欢欢的跳远成绩=第三次乐乐的跳远成绩是欢欢的几分之几;
(3)观察折线统计图,实线表示欢欢数据,折线往上坡度越陡表示上升幅度越大,据此分析;
(4)根据折线统计图的变化,折线往上表示上升趋势,折线往下表示下降趋势,派跳远成绩稳定且呈上升趋势的去参加跳远比赛。
【详解】(1)110-95=15(厘米)
两人第二次跳远成绩相差15厘米,第5次相差最多。
(2)95÷105==
第三次乐乐的跳远成绩是欢欢的。
(3)欢欢训练中第2次到第3次上升的幅度最大。
(4)学校要派一名同学参加区里的跳远比赛,欢欢更加合适。因为欢欢的成绩在稳步提升。(答案不唯一)
12.(1)35
(2)2006;7
(3)见详解
【分析】(1)在这五届冬季奥运会上,中国在冰上项目中获得的奖牌数量分别是9枚、8枚、7枚、5枚、6枚,把它们相加即可解答。
(2)观察折线统计图可知,2006年冰上项目获得奖牌9枚,雪上项目获得奖牌2枚,数量相差最多;9-2=7(枚),即相差7枚。
(3)从统计图中可以看出,在这五届冬季奥运会上,中国在冰上项目中获得的奖牌数量几乎逐届减少,而雪上项目获得的奖牌数量整体趋势是不断增加,据此可以预测:下一届冬季奥运会中国冰上项目获得的奖牌数量可能是5到7枚,雪上项目获得奖牌的数量还会增加。
【详解】(1)9+8+7+5+6=35(枚),则在这五届冬季奥运会上,中国在冰上项目中共获得35枚奖牌。
(2)9-2=7(枚),冰上项目和雪上项目获得奖牌数量相差最多的是2006年冬季奥运会,相差7枚。
(3)可以预测:下一届冬季奥运会中国冰上项目获得的奖牌数量可能是5到7枚,雪上项目获得奖牌的数量还会增加。因为在这五届冬季奥运会上,中国在冰上项目中获得的奖牌数量几乎逐届减少,而雪上项目获得的奖牌数量整体趋势是不断增加。(答案不唯一)
13.(1)4;4
(2)
(3)18;20
(4)第10天时芽的长度是根的几分之几?
【分析】(1)观察复式折线统计图,实线表示根的生长情况,虚线表示芽的生产情况,折线开始上升出表示开始生根和发芽,据此确定生根和发芽需要的天数,发芽需要的天数-生根需要的天数=生根后需要几天发芽;www-2-1-cnjy-com
(2)将第12天时根的长度看作单位“1”,第12天时芽的长度÷根的长度=第12天时芽的长度是根的几分之几;
(3)观察复式折线统计图,折线往上坡度越陡表示长得越快,据此分析;
(4)答案不唯一,合理即可,可以模仿第(2)小题提一个类似的问题。如第10天时芽的长度是根的几分之几?将第10天时根的长度看作单位“1”,第10天时芽的长度÷根的长度=第10天时芽的长度是根的几分之几。
【详解】(1)8-4=4(天)
水仙花球第4天开始生根,再过4天开始发芽。
(2)20÷52==
第12天时芽的长度是根的。
(3)第18天到第20天时根和芽长得最快。
(4)第10天时芽的长度是根的几分之几?
10÷40==
答:第10天时芽的长度是根的。
14.(1)图见详解;
(2)2022;2023;
(3)450;
(4)见详解
【详解】(1)将题目中的数据对应年份描点,然后将点和点依次连接起来。
(2)用减法求出相邻两年的数据差,再比较。
(3)根据折线统计图一直上升的局势,得出合理的数据即可。
(4)根据分析写出合理的原因。
【解答】(1)
(2)220-200=20(万人)
280-220=60(万人)
350-280=70(万人)
70>60>20
从图中看出,从2022到2023年,游客人数增加最多。
(3)结合该城市旅游人数的变化情况,预估2024年该市游客人数将达450万人(答案不唯一)。
(4)疫情过后旅游的人数由少逐渐变多;
人们更向往外面的世界。(答案不唯一)
15.(1)14;8
(2)8
(3)五(1)班
【分析】(1)观察复式折线统计图,实线表示五(1)班成绩,虚线表示五(2)班成绩,分别将两个班成绩高于8分的人数相加即可。21教育名师原创作品
(2)观察复式折线统计图,实线表示五(1)班成绩,10分有1人,是第1名,9分有13人,是前1+13=14(名),8分有10人,14+10=24(名),是第15名到第24名,据此分析。
(3)根据平均数=总数÷份数,分别计算出两个班的平均分,比较即可。
【详解】(1)13+1=14(人)、6+2=8(人)
若成绩高于8分的为优秀,五(1)班比赛成绩优秀的人数有14人,五(2)班比赛成绩优秀的人数有8人。
(2)1+13=14(名)、14+10=24(名)
第15名到第24名都是8分,琪琪的成绩是五(1)班的第20名,她的成绩是8分。
(3)五(1)班的平均分:(9×6+7×7+10×8+13×9+1×10)÷(9+7+10+13+1)
=(54+49+80+117+10)÷40
=310÷40
=7.75(分)
五(2)班的平均分:(11×6+12×7+9×8+6×9+2×10)÷(11+12+9+6+2)
=(66+84+72+54+20)÷40
=296÷40
=7.4(分)
7.75>7.4
答:从平均分来看,五(1)班对茶文化掌握得更好。
16.(1)见详解
(2)①下降
②2018;39亿
③同意;理由见详解
【分析】(1)实线表示公共汽车数据,虚线表示地铁数据;根据各数量的多少,在方格图的纵、横的交点上描出表示数量多少的点;把各点用线段顺次连接起来。
(2)①实线表示公共汽车数据,折线往上表示上升趋势,折线往下表示下降趋势,据此填空;
②同一年份,两数据点相距越远表示客运量相差越多,据此确定客运量相差最多的年份,再求出这一年公共汽车和地铁客运量的差即可。【版权所有:21教育】
③根据折线统计图折线上升和下降的变化趋势进行分析,折线往上表示上升趋势,说明人数越来越多,据此解答。
【详解】(1)某市2018~2023年公共汽车和地铁的客运量情况统计图
(2)①2018~2023年,公共汽车客运量整体呈下降趋势。
②55-16=39(亿人)
2018~2023年,公共汽车和地铁的客运量相差最多的是2018年,相差了39亿人次。
③同意他的说法,因为选择地铁出行的人数呈上升趋势,选择公共汽车出行的人数呈下降趋势,从2021年开始已经超过选择公共汽车出行的人数。(理由答案不唯一)
17.(1)见详解
(2)1
(3)
(4)5月份货车的销售量是轿车的几分之几?(答案不唯一)
【分析】(1)先确定图例,用实线表示轿车的销售情况,用虚线表示货车的销售情况;再结合统计表中数据的大小,分别描出两组数据的各点,并根据图例把各点用线段顺次连接起来,完成复式折线统计图的绘制。
(2)观察复式折线统计图,两条折线的叉口最大时,表示这个月两种车销售量相差最大。
(3)从图中可知,2月份轿车销售250辆,货车销售150辆,用货车的销售量除以轿车的销售量,即是2月份货车的销售量是轿车的几分之几。
(4)结合复式折线统计图提供的信息,提出问题,并解答,合理即可。
如提问:5月份货车的销售量是轿车的几分之几?
用5月份货车的销售量除以轿车的销售量即可。
【详解】(1)如图:
(2)两种车销售量相差最大的是1月。
(3)150÷250=
2月份货车的销售量是轿车的。
(4)提问:5月份货车的销售量是轿车的几分之几?(答案不唯一)
100÷200=
答:5月份货车的销售量是轿车的。
18.(1)5;3
(2)(3)见详解
【分析】(1)通过观察统计图可知,奇思和妙想第5天的成绩相差最大,根据求一个数比另一个数多或少几,用减法解答;
(2)观察折线统计图的走向,所用时间越少,说明进步越大;据此判断两人成绩呈现上升或下降的变化趋势,再进一步观察谁的进步幅度大些。
(3)比赛的时候,奇思的成绩可能比妙想的好,可以预测奇思的比赛成绩和妙想的比赛成绩。
【详解】(1)24-21=3(秒)
奇思和妙想第5天的成绩相差最大,相差3秒。
(2)两人成绩呈现上升的变化趋势,奇思的进步幅度大些。
(3)可以预测奇思的比赛成绩可能是17秒,妙想的比赛成绩可能是18秒。(答案不唯一)
19.(1)不仅可以表示数量的多少,而且可以反映数据的增减变化情况.
(2)4km,小时,8千米/时
(3)
【详解】(1)不仅可以表示数量的多少,而且可以反映数据的增减变化情况.
(2)小明家距离图书馆4千米
由统计图的水平线的起止时间相减即可得到在图书馆看书的时间
100﹣30=70(分钟)=(小时)
运用路程4千米除以时间(30分钟=0.5小时)等于速度即可进行计算.
4÷(30÷60)=8(千米/时)
(3)
20.(1)8000立方米
(2)能在当天10:30之前加完气;详解见解析
【分析】整个过程相当于储气罐里的天然气先增加,后减少,起始时刻,储气罐里的天然气是原来就要的,最高的是燃气公司给储气罐注入天然气结束时的数量;根据天然气的减少的速度,可以求出给每辆车加气需要的时间,然后求出给所有车加完气需要的时间,进行比较。
【详解】(1)(立方米)
答:燃气公司向储气罐注入了8000立方米的天然气。
(2)8点半开始加气,从10000立方米下降到8000立方米,下降了2000立方米,使用时间是10小时,可以求出加气的速度;
(立方米)
每小时加气200立方米,8点半距离10点半有2小时;
(立方米)
(辆)
10点半之前可供20辆车加气完成,所以第18辆车可以在当天10:30之前加完气。
【点睛】本题是将折线统计图与实际问题相结合,首先要充分理解统计图所表示的含义,然后再求解问题。
21.(1)16
(2)12
(3)
【分析】在表示路程和时间的行程问题的折线统计图中,折线上升,表示向目的地运动;折线呈水平方向,表示在某地停留,折线下降,表示向出发地运动。据此可解答。
(1)运动4秒,运动的长是2×4=8(厘米),宽是2厘米,重叠部分的面积是长方形8×2=16(平方厘米),据此可解答。
(2)根据题意看图,第6秒以后,重叠部分开始不变,即正方形的边长是6×2=12(厘米),据此解答即可。
(3)当长方形的左端,刚好穿过正方形时,还需要8+2=10(秒)。所以第一个括号填10。
长方形的左端完全离开正方形,相当于火车行程问题,(20+12) +2=16(秒)
所以第二个括号填16,没有重叠部分,面积为0。
【详解】(1)8×2=16(平方厘米)
(2)6×2=12(厘米)
(3)
【点睛】这里有行程问题,折线统计图问题,通过折线统计图分析长方形纸条和正方形重叠部分的面积与运动时间是解题的关键。
22.(1)10;24
(2)3.6升
(3)10分钟;作图见详解
【分析】(1)观察统计图,折线往上坡度变陡,说明同时打开了两根进水管;根据长方体体积=底面积×高,求出水的体积即可。
(2)求出10至20分钟的注水量,除以分钟数即可。
(3)先求出容器剩余容积,除以A管每分钟注水量就是继续注水将容器注满的时间,补充统计图即可。
【详解】(1)800×30=24000(立方厘米)=24(升)
10分钟后同时打开A、B两管,当时容器里的有24升水。
(2)800×(75-30)÷(20-10)
=800×45÷10
=3600(立方厘米)=3.6(升)
答:每分钟注入3.6升水。
(3)800×(105-75)
=800×30
=24000(立方厘米)=24(升)
24÷(24÷10)
=24÷2.4
=10(分钟)
答:10分钟后可将容器注满。
【点睛】关键是掌握长方体体积公式,折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
23.(1)2015;2016;131;
(2)2016;809;2021;48;
(3)(4)见详解
【分析】(1)结合统计图可知,出生人口呈增长趋势的是从2011年到2016年,其中,折线坡度最陡的一段,就表示相邻的这两年中,出生人口增长最快;这两年是从2015年到2016年;再用靠后年份对应的出生人口数减去靠前年份对应的出生人口数,得到具体增长了几万人;
(2)折线统计图中,表示同一年度出生人数和死亡人数的两个点距离越长,两数相差越大,从图上看出出生和死亡人数相差较大的是2016年和2017年;分别求得这两年出生人口数和死亡人口数的差,比较大小,较大的就是所求;【来源:21cnj*y.co*m】
同理:表示同一年度出生人数和死亡人数的两个点距离越短,两数相差越小,从图上看出是2021年,把这两年的人口数作差,就是所求;
(3)可结合统计图中,实线虚线的具体走势所代表的出生人口与死亡人口的变化,来解释国家为什么会在2015年提出“二胎”政策、2021年提出“三孩”政策;
(4)可结合“三孩”政策提出可能产生的效果,以及统计图中虚线较缓的走势来分析预测。
【详解】(1)1786-1655=131(万人)
相邻的两年中,出生人口数增长最快的是从(2015)年到(2016)年,增长了(131)万人。
(2)2016年相差:1786-977=809(万人)
2017年相差:1723-986=737(万人)
809>737,所以2016年出生人口数与死亡人口数相差最多。
2021年相差:1062-1014=48(万人)
出生人口数和死亡人口数相差最多的是(2016)年,相差(809)万人;出生人口数和死亡人口数相差最少的是(2021)年,相差(48)万人。【来源:21·世纪·教育·网】
(3)从统计图可看出2015年之前人口增长过慢,而死亡人口数在不断增长,说明人口老龄化严重,子女赡养压力增大,所以提出“二胎”政策;
而2015年提出“二胎”政策后,2016年出生人口数有所增长,但之后就持续减少,所以2021年又提出了“三孩”政策。
(4)预测未来五年我国出生人口数将有所增长,因为2021年提出了“三孩”政策。按照统计图中的变化趋势,未来五年我国死亡人口数也将成缓慢增长趋势。
【点睛】本题较为复杂,结合统计图分析现状,需要仔细读图和大量计算;结合实际来预测需要学生充分理解题意并展开想象。
24.(1)12;
(2)5秒或13秒
【分析】(1)由重叠面积与时间的关系图知,长方形每秒移12÷2÷3=2(厘米),当从第6秒开始,重叠面积没发生变化,说明长方形的右边宽的部分已经移到正方形的右边,此时移动:2×6=12(厘米),所以正方形边长为12厘米;
(2)当长方形从正方形左边移到右边时,会有两个时刻与正方形的重叠面积是30平方厘米,第一个时刻是长方形刚移到正方形内时,此时长方形的右半部分与正方形重叠,此时移动(30÷3=10)厘米,用(10÷ 2=5秒);第二个时刻是长方形从正方形内移出时,此时长方形只剩左半部分与正方形重叠,还有(30÷3=10)厘米在正方形内,共移[24+(12-10)=26]厘米,用(26÷2=13)秒。
【详解】(1)12 ÷2÷3
=6÷3
=2(厘米)
长方形每秒移动2厘米,正方形的边长是运行6秒后的长度:
2×6=12(厘米)
所以,正方形的边长为12厘米。
(2)正方形的重叠面积是30平方厘米,
30÷3=10(厘米)
10÷2=5(秒)
第一个时刻是长方形刚移到正方形内时,此时长方形的右半部分与正方形重叠,此时移动了10厘米,用了5秒;21教育网
30÷3=10(厘米)
24+2=26(厘米)
26÷2=13(秒)
第二个时刻是长方形从正方形内移出时,此时长方形只剩左半部分与正方形重叠,还有10厘米在正方形内,共移动了26厘米,用了13秒。
答:当平移时间为5秒或13秒时,长方形和正方形的重叠部分面积是30平方厘米。
【点睛】此题考查了匀速运动这一知识,以及分析折线统计图的能力。
25.6.4小时或6.8小时
【分析】从图中可知,甲、乙两地的距离是120千米;王叔叔骑车从甲地到乙地中间休息了1小时,到达目的地用时(9-1)小时;刘叔叔开车从乙地到甲地用时(8-6)小时;根据“速度=路程÷时间”,分别求王叔叔骑车的速度和刘叔叔开车的速度。
当刘叔叔出发时,王叔叔骑车已行了(6-1)小时,根据“路程=速度×时间”求出王叔叔先行的路程;再用全程减去王叔叔先行的路程,即是当刘叔叔出发时两人相距的距离。
求王叔叔出发多少小时后与刘叔叔相距15千米,分两种情况:
情况一:两人相遇前相距15千米时,用刘叔叔出发时两人相距的距离减去15,即是两人相遇前行的路程之和,再除以两人的速度和,求出两人相距15千米时行的时间,最后加上王叔叔早出发的6小时即可;
情况二:两人相遇后相距15千米时,用刘叔叔出发时两人相距的距离加上15,即是两人相遇前行的路程之和,再除以两人的速度和,求出两人相距15千米时行的时间,最后加上王叔叔早出发的6小时即可。
【详解】刘叔叔开车的速度:
120÷(8-6)
=120÷2
=60(千米/时)
王叔叔骑车的速度:
120÷(9-1)
=120÷8
=15(千米/时)
当刘叔叔出发时,两人相距:
120-15×(6-1)
=120-15×5
=120-75
=45(千米)
情况一:两人相遇前相距15千米
(45-15)÷(60+15)
=30÷75
=0.4(小时)
6+0.4=6.4(小时)
情况二:两人相遇后相距15千米
(45+15)÷(60+15)
=60÷75
=0.8(小时)
6+0.8=6.8(小时)
答:王叔叔出发6.4小时或6.8小时后与刘叔叔相距15千米。
【点睛】先从时间与距离的关系图中获取信息,根据速度、时间、路程之间的关系分别求出两人的速度以及刘叔叔出发时两人相距的距离;然后分两种情况讨论两人何时相距15千米是解题的关键。【出处:21教育名师】
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
