(核心素养应用意识)第七单元图形的运动(二)(解决问题)(含解析)-四年级数学下册人教版
文档属性
| 名称 | (核心素养应用意识)第七单元图形的运动(二)(解决问题)(含解析)-四年级数学下册人教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览

文档简介
/ 让教学更有效 精品试卷 | 数学学科
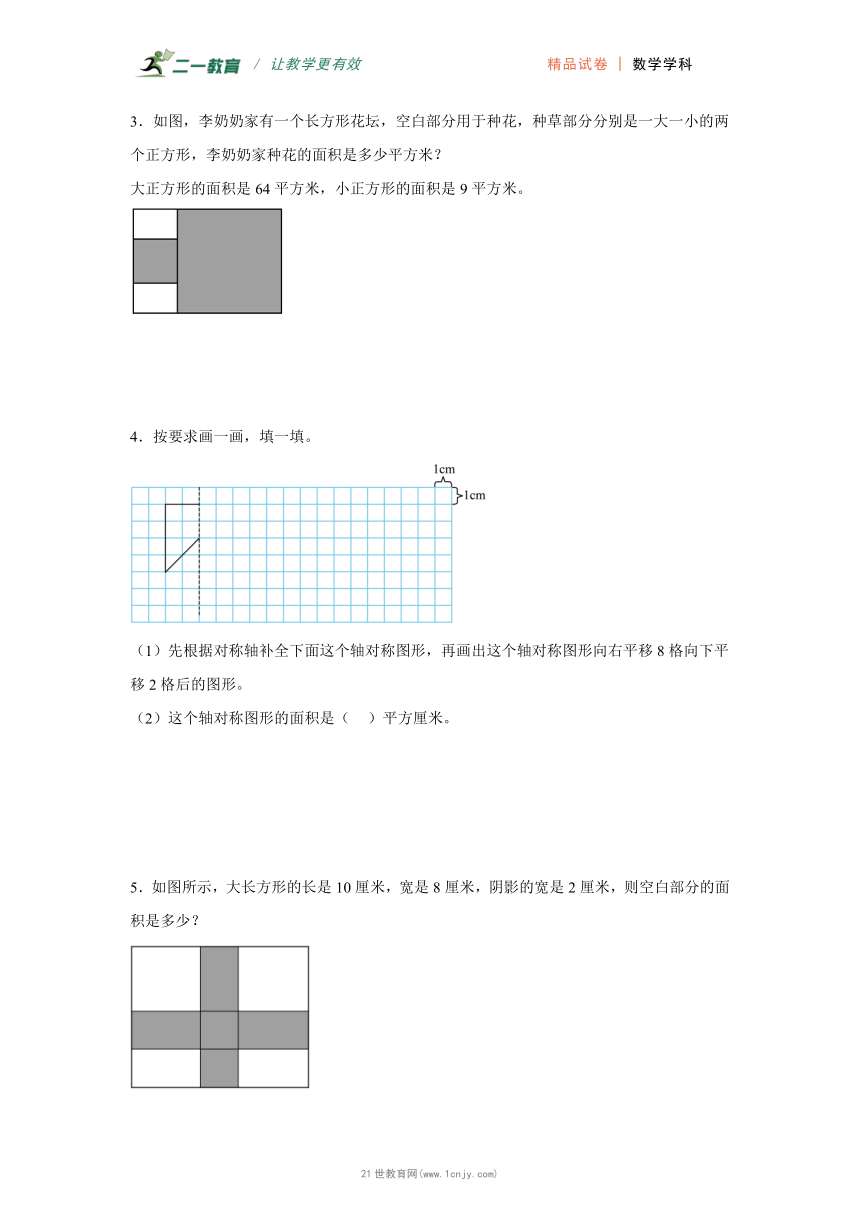
第七单元图形的运动(二)
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.想一想,画一画。
(1)在下面格子图中画出下边立体图形从上面看到的图形。
(2)如果添上1个小正方形,使刚才画的图形成为一个轴对称图形,共有( )种不同的添加方法。请在下面方格图中画出其中一种添法。
2.小东出门前和回来时从镜子里看到的钟表指针分别如右图所示,你知道他最少出去了多长时间吗?
3.如图,李奶奶家有一个长方形花坛,空白部分用于种花,种草部分分别是一大一小的两个正方形,李奶奶家种花的面积是多少平方米?
大正方形的面积是64平方米,小正方形的面积是9平方米。
4.按要求画一画,填一填。
(1)先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移8格向下平移2格后的图形。
(2)这个轴对称图形的面积是( )平方厘米。
5.如图所示,大长方形的长是10厘米,宽是8厘米,阴影的宽是2厘米,则空白部分的面积是多少?
6.如图,一个边长为20厘米的正方形,上面横竖各有两张长方形纸条,形成一个“井”字,纸条宽都是2厘米。求“井”字部分的面积。21教育名师原创作品
7.小动物们分别向哪个方向平移?平移多少格才能吃到它们喜欢的食物?
8.求小路的占地面积。
如图所示:一块长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路。
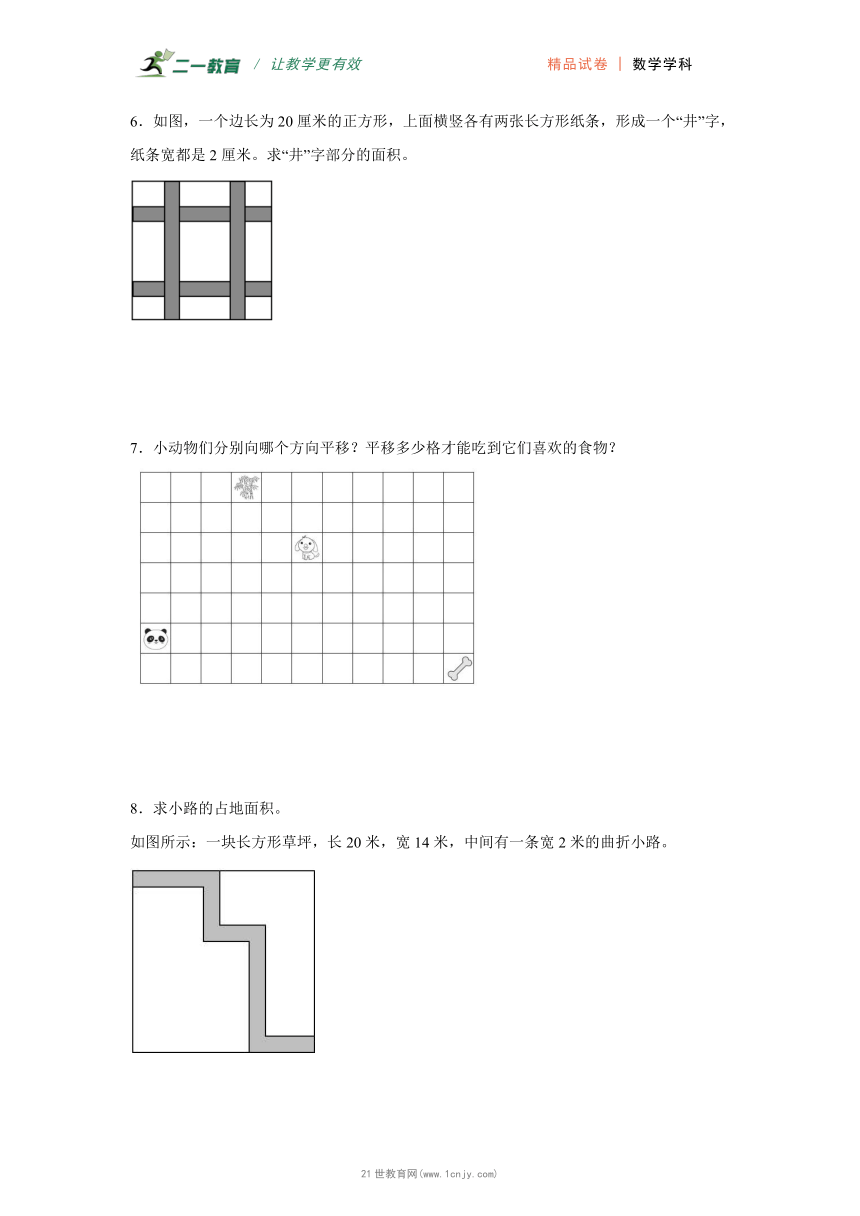
9.认真读题画一画,填一填。
(1)画出①号三角形AB边上的高。
(2)以虚线为对称轴画出①号三角形轴对称图形的另一半。
(3)②号图形的面积是( )平方厘米。(每个小方格的边长为1厘米)
(4)画出②号图形向下平移4格再向右平移3格后的图形。
10.下图中正方形的周长是48厘米,中间有一个长方形,长方形的四个顶点恰好把正方形每边分为两段,其中长的那段是短的长度的2倍,则长方形的面积是多少平方厘米?
11.校园劳动基地的①号地和②号地种小白菜(如图)。小白菜地的面积是多少平方米?写出求面积的具体方法,再计算出结果。【来源:21·世纪·教育·网】
12.一块正方形的花园,它的边长是20米。在花园里横竖各有二条走道,如图,走道宽都是2米。问这块花园种花的面积是多少平方米?
13.如图,一块长方形花圃中间有两条宽度相等的小路(每条小路间距均匀)。这块花圃种花的面积是多少平方米?
14.下图是小娅家和图书馆所在位置的平面图。小娅沿着图中的实线道路,准备从家步行到图书馆。她先走了3分钟,每分钟走84米。21*cnjy*com
(1)小娅家到图书馆的路程共多少米?
(2)小娅还要走多少米才能到达图书馆?
15.将三角形ABC向右平移后得到三角形,如果∠1=45°,∠2=104°,请求出∠3的度数。
16.剪纸是中国古老的民间艺术之一。下面是小明同学剪出的一个花边图形,你能计算出阴影部分的面积吗?
17.学校艺术楼门前要建一个如图所示长12米,宽2米的花坛,如果在花坛边铺一条小路,求小路长多少米?2·1·c·n·j·y
18.按要求完成题目。
(1)算一算:图1的面积是多少?图2的周长是多少?
(2)选词填空:我们是运用( )的方法,通过图形的运动,把不规则的平面图形( )为长方形,使得问题顺利解决。(“平移”“转化”)2-1-c-n-j-y
19.方格图每个小方格边长是1cm。小伍说:“直线l是平行四边形ABCD的对称轴。”小伍说得对吗?请你用轴对称图形的特征说明理由。
20.正六边形作为中国传统形状,象征六合、六顺之意,常被家居配饰所用,如首饰盒、古建的窗户、古井的口、佛塔等等。如图,在古建筑中经常会看到这样的正六边形窗户。
(1)用数学的眼光观察,这个窗户的正六边形外框有( )条对称轴。
(2)请根据已有的经验,探究下面六边形的内角和,并把思考过程用自己喜欢的方式表示出来。(提示:可以画一画、算一算、写一写……)
21.剪纸是中国古老的民间艺术之一。下面是小玲剪的一个花边图形,你能计算出阴影部分的面积吗?
22.求下面图形中阴影部分的面积。
23.按要求完成下面各题。(每个小方格的边长表示1厘米)
(1)根据对称轴补全上面这个轴对称图形。
(2)这个轴对称图形的周长是( )厘米。
(3)画出这个轴对称图形向左平移4格后的图形。
24.按要求完成下面题目。
(1)先从ABCD四个点中任选3个点画一个三角形。这是一个( )三角形。
(2)然后画出三角形向下平移6格后的图形。
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。
(4)画出轴对称图形的另一半。
《(核心素养应用意识)第七单元图形的运动(二)(解决问题)-四年级数学下册人教版》参考答案
1.(1)见详解
(2)4;见详解
【分析】(1)根据题意,从上面看到三竖列,第一竖列有2个小正方形,第二竖列有2个小正方形,第三竖列有1个小正方形,这三竖列上面对齐。【来源:21cnj*y.co*m】
(2)下图中4个位置添上1个小正方形,都能使其成为一个轴对称图形。
【详解】根据分析可知:
(1)先观察,再根据观察的结果作图如下:
(2)如果添上1个小正方形,使刚才画的图形成为一个轴对称图形,共有4种不同的添加方法,其中的一种添法如下:
2.4小时
【分析】根据题意,在镜子中看到的时刻与真实时刻因为对称的,出门前从镜子里看到的钟表时间时针对着9,分钟对着12,是9时,那么实际时间是3时;回来时从镜子里看到的钟表时间时针对着5,分钟对着12,是5时,那么实际时间是7时。经过时间=结束时间-开始时间,12时-从镜子里看到的时间=实际的时间,据此解答。
【详解】根据分析可知:
出门前的时间12-9=3(时)
回来的时间12-5=7(时)
7-3=4(小时)
答:他最少出去了4小时。
3.15平方米
【分析】正方形的面积=边长×边长。由题意得,大正方形的面积是64平方米,因为64=8×8,所以大正方形的边长是8米。小正方形的面积是9平方米,9=3×3,则小正方形的边长是3米。然后再把小正方形平移到上面,则种花的两部分合并成一个长方形(如下图)。
由图可知,长方形的长是8-3=5(米),宽是3米。长方形的面积=长×宽,直接将数据代入即可算出种花的面积。
【详解】64=8×8,则大正方形的边长是8米。
9=3×3,则小正方形的边长是3米。
(8-3)×3
=5×3
=15(平方米)
答:李奶奶家种花的面积是15平方米。
4.(1)见详解;(2)12
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)图中每格是边长1厘米的正方形面积是1平方厘米,数出有几个整格,再数出有几个半格,2个半格合成1个整格,再相加即为轴对称图形的面积。www-2-1-cnjy-com
【详解】(1)如图:
(2)10个整格,4个半格是4÷2=2(个)整格,合起来是10+2=12(个)
即这个轴对称图形的面积是12平方厘米。
5.48平方厘米
【分析】把横条向下平移到下边,把竖条向左平移到左边,这时空白部分是一整块长方形,长是(10-2)厘米,宽是(8-2)厘米,根据长方形面积=长×宽,带入数值即可解答。
【详解】(10-2)×(8-2)
=8×6
=48(平方厘米)
答:空白部分的面积是48平方厘米。
6.144平方厘米
【分析】如果求一道纸条的面积,比较好求,20×2=40(平方厘米),但是其中有多个交叉重叠部分,直接求解有一定难度,这时可以通过平移,将横向纸条向上或向下平移,将纵向纸条向左或右平移,形成如图形。www.21-cn-jy.com
中间白色部分是一个边长为20-2×2=20-4=16厘米的正方形,用大正方形的面积减去白色部分的面积,就是“井”字部分的面积。
【详解】20×20-(20-2×2)×(20-2×2)
=20×20-(20-4)×(20-4)
=20×20-16×16
=400-256
=144(平方厘米)。
答:“井”字部分的面积是144平方厘米。
7.见详解
【分析】先要观察图中的两种食物,一种是熊猫喜欢吃的竹子,另一种是小狗喜欢吃的骨头。然后把相对应的动物和食物的位置作比较,判断出平移的方向和距离。
【详解】熊猫先向右平移3格,再向上平移5格(或先向上平移5格,再向右平移3格)就可以吃到竹子;小狗先向下平移4格,再向右平移5格(或先向右平移5格,再向下平移4格)就可以吃到骨头。
8.64平方米
【分析】通过平移,将图形变为如下图:
据此可知,小路的面积相当于长方形草坪的面积减去长为(20-2)米、宽为(14-2)米的长方形面积;根据长方形的面积=长×宽,代入数据解答。
【详解】20×14-(20-2)×(14-2)
=20×14-18×12
=280-216
=64(平方米)
答:小路的占地面积是64平方米。
9.(1)(2)(4)图见详解
(3)6
【分析】(1)根据三角形高的意义,延长三角形ABC的边AB到D,再根据过直线外一点画已知直线的垂线的方法,从点C向AB的延长线画垂线段,与其交于点E,CE就是AB边上的高,由此作图即可;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可;
(3)通过平移可知,②号图形的面积等于长3厘米、宽2厘米的长方形的面积,长方形的面积=长×宽,依此计算;
(4)根据平移的特征,把②号图形的各顶点分别向下平移4格,再向右平移3格,依次连接即可得到平移后的图形。
【详解】(1)(2)(4)作图如下:
(3)3×2=6(平方厘米)
②号图形的面积是6平方厘米。
10.64平方厘米
【分析】根据正方形的周长÷4=边长,代入数据即可求出正方形的边长,因为长的那段是短的长度的2倍。所以正方形的边长是短的长度的(2+1)倍,据此用除法求出短的长度,再用减法求出长的部分的长度;长方形的面积相当于正方形的面积减去4个三角形的面积和,4个三角形通过拼接可以拼成2个正方形,其中1个边长等于短的长度,另一个边长等于长的部分的长度,根据正方形的面积=边长×边长,分别求出2个正方形的面积,再求出它们的和;进而求出大正方形的面积,然后用减法即可求出长方形的面积。
【详解】边长:48÷4=12(厘米)
短:12÷(2+1)
=12÷3
=4(厘米)
长:12-4=8(厘米)
三角形:4×4+8×8
=16+64
=80(平方厘米)
大正方形:12×12=144(平方厘米)
长方形:144-80=64(平方厘米)
答:长方形的面积是64平方厘米。
【点睛】本题考查了平面图形的知识的应用,掌握相关的公式以及转化、平移等解题技巧是解答本题的关键。
11.24平方米;把①号地向右平移1个格后,①号地与②号地拼成一个长6米,宽4米的长方形
【分析】如图:
根据题意,两个点之间的距离是1米,把①号地向右平移1个格后,①号地与②号地拼成一个长6米,宽4米的长方形,根据长方形的面积=长×宽,解答即可。
【详解】把①号地向右平移1个格后,①号地与②号地拼成一个长6米,宽4米的长方形。
6×4=24(平方米)
答:小白菜地的面积是24平方米。
12.256平方米
【分析】这个正方形的花园里横竖各有二条宽都是2米走道,把4条走道平移到花园的边上,中间部分就为种花的部分。由图可知中间种花的部分为一个正方形,正方形的边长为花园的边长减去2个走道的宽,根据正方形的面积公式:正方形面积=边长×边长,求出种花的面积。21·世纪*教育网
【详解】20-2×2
=20-4
=16(米)
16×16=256(平方米)
答:这块花园种花的面积是256平方米。
13.1620平方米
【分析】由题意得,长方形花圃的长是56米,宽是30米。它的中间有两条宽度相等的小路且每条小路的间距为1米,两条小路将长方形分成了三部分。如果将两边的部分向中间平移,那么这个花圃就组成了一个新的长方形。这个长方形的长是(56-1-1)米,宽是30米。长方形的面积=长×宽,直接将数据代入即可算出这块花圃种花的面积。
【详解】(56-1-1)×30
=(55-1)×30
=54×30
=1620(平方米)
答:这块花圃种花的面积是1620平方米。
14.(1)656米
(2)404米
【分析】(1)从图中可以看出,从小娅家到图书馆的路线通过平移,可转变为一条宽和一条长,所以求出图中长加宽的和就是小娅家到图书馆的路程。21*cnjy*com
(2)已知小娅先走了3分钟,每分钟走84米,根据速度×时间=路程,可以求出先走了的路程,即(84×3)米,再用总路程减走了的路程,即得到还要走的路程。据此解答。
【详解】(1)206+450=656(米)
答:小娅家到图书馆的路程共656米。
(2)656-3×84
=656-252
=404(米)
答:小娅还要走404米才能到达图书馆。
15.31°
【分析】由题意得,将三角形ABC向右平移后得到三角形,∠1=45°,所以=45°。∠2、∠3和组成了一个平角,求∠3的度数,直接用180°减去∠2再减去的度数即可解答。【版权所有:21教育】
【详解】∠3=180°-104°-45°
=76°-45°
=31°
答:∠3的度数是31°。
16.12平方厘米
【分析】由图可知,每两个正方形中的阴影部分合起来可以组成一个完整的正方形,整个图中的阴影部分可以组成三个完整的正方形。正方形的面积=边长×边长,可以先用2乘2算出一个正方形的面积,再乘3即可算出三个正方形的面积是多少平方厘米。
【详解】2×2×3=4×3=12(平方厘米)
答:阴影部分的面积是12平方厘米。
17.28米
【分析】把各不规则部分的横线段和竖线段进行平移,可得到所求周长恰好是长为12米,宽为2米的长方形的周长,用(长+宽)×2,即可求出小路长。21cnjy.com
【详解】(12+2)×2
=14×2
=28(米)
答:小路长28米。
【点睛】此题主要考查学生对矩形两组对边对应相等的性质的掌握情况,做这类题时还需注意利用平移的思想。
18.(1)图1的面积是20平方厘米,图2的周长是18厘米。
(2)平移;转化
【分析】(1)图1是不规则图形,但通过观察发现这是一个上下对称的轴对称图形,可以利用平移的方法将其变成规则图形后求面积。图2的周长也可以用平移的方法将其转化成长方形后再求其周长。21世纪教育网版权所有
(2)根据(1)中的思路来选词进行填空即可。
【详解】(1)如图,将图形用虚线进行分割,将虚线右边图形向左进行平移5格后,便组成了一个长为5厘米,宽为4厘米的长方形。根据长方形面积=长×宽,可知该图形面积=5×4=20(平方厘米)
如图,将该图形的横向线段分别向上进行平移,纵向线段分别向右平移后,该图形就变成了一个长是5厘米,宽是4厘米的长方形,根据长方形的周长=(长+宽)×2可知,该图形周长=(5+4)×2=9×2=18(厘米)
答:图1的面积是20平方厘米,图2的周长是18厘米。
(2)根据(1)的方法可知,我们是运用平移的方法,通过图形的运动,把不规则的平面图形转化为长方形,使得问题顺利解决。
19.小伍说得不对;因为点和点到直线的距离不相等。
【分析】轴对称图形的特点是:如果一个图形沿某条直线对折后,能够与自身完全重合,那么这个图形就是轴对称图形,这条直线就是对称轴。对于平行四边形来说,只有当它是特殊的平行四边形(如矩形或菱形)时,才可能有对称轴。一般的平行四边形没有对称轴,因此直线l不可能是平行四边形ABCD的对称轴。
【详解】根据分析得:小伍说得不对;因为点D和点C到直线l的距离不相等。
20.(1)6
(2)720°
【分析】(1)这个六边形窗户的外框是轴对称图形,找出它的对称轴,要使对称轴左右两边的图形完全相同。可分别过这个六边形窗户的外框的两个相对的顶点,或过这个六边形窗户的外框的两个相对的边的中点,画出它的对称轴;
(2)一个三角形的内角和为180°,正六边形可被分成4个三角形,用180°×4,即可得到这个正六边形的内角和是多少度。
【详解】(1)过这个六边形窗户的外框的两个相对的顶点,可画出它的对称轴,这样的对称轴有3条;过这个六边形窗户的外框的两个相对的边的中点,可画出它的对称轴,这样的对称轴有3条。因此这个六边形窗户的外框共有6条对称轴。
(2)180×4=720°
因此这个正六边形的内角和是720°。
21.16平方厘米
【分析】通过观察图形可知,阴影部分的面积可以通过平移“转化”为边长是2厘米的4个正方形的面积。根据正方形的面积=边长×边长,把数据代入公式,即可解题。
【详解】由分析可知:
2×2×4
=4×4
=16(平方厘米)
答:阴影部分的面积是16平方厘米。
22.12平方分米
【分析】观察图片可以发现相邻两个图形,阴影部分通过平移可以组成一个完整的正方形,相邻图形的两两组合,可以组成三个正方形,正方形的面积=边长×边长,求出一个正方形面积再乘3即为所求。21教育网
【详解】2×2×3
=4×3
=12(平方分米)
答:图形中阴影部分的面积是12平方分米。
23.(1)(3)见详解
(2)12
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴虚线的下边画出上半图的关键对称点,依次连接即可。
(2)由图可知,这个图形的一周有12个小方格的边长,所以它的周长是12厘米。
(3)根据平移的特征,把这个轴对称图形的各顶点分别向左平移4格,依次连接即可得到平移后的图形。
【详解】(1)(3)如图
;
(2)这个轴对称图形的周长是12厘米。
24.(1)图见详解;等腰;
(2)(3)(4)见详解
【分析】(1)先从ABCD四个点中任选3个点画一个三角形(画法不唯一),等腰三角形的两腰相等,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底,依此画图。21·cn·jy·com
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
(3)根据三角形高的意义,在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高,再根据过直线外一点画已知条直线的垂线的方法,由此作图即可。【出处:21教育名师】
(4)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)先从ABCD四个点中任选3个点画一个三角形。如图:
这是一个等腰三角形。
(2)然后画出三角形向下平移6格后的图形。如图:
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。如图:
(4)画出轴对称图形的另一半。如图:
(三角形画法不唯一)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
第七单元图形的运动(二)
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.想一想,画一画。
(1)在下面格子图中画出下边立体图形从上面看到的图形。
(2)如果添上1个小正方形,使刚才画的图形成为一个轴对称图形,共有( )种不同的添加方法。请在下面方格图中画出其中一种添法。
2.小东出门前和回来时从镜子里看到的钟表指针分别如右图所示,你知道他最少出去了多长时间吗?
3.如图,李奶奶家有一个长方形花坛,空白部分用于种花,种草部分分别是一大一小的两个正方形,李奶奶家种花的面积是多少平方米?
大正方形的面积是64平方米,小正方形的面积是9平方米。
4.按要求画一画,填一填。
(1)先根据对称轴补全下面这个轴对称图形,再画出这个轴对称图形向右平移8格向下平移2格后的图形。
(2)这个轴对称图形的面积是( )平方厘米。
5.如图所示,大长方形的长是10厘米,宽是8厘米,阴影的宽是2厘米,则空白部分的面积是多少?
6.如图,一个边长为20厘米的正方形,上面横竖各有两张长方形纸条,形成一个“井”字,纸条宽都是2厘米。求“井”字部分的面积。21教育名师原创作品
7.小动物们分别向哪个方向平移?平移多少格才能吃到它们喜欢的食物?
8.求小路的占地面积。
如图所示:一块长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路。
9.认真读题画一画,填一填。
(1)画出①号三角形AB边上的高。
(2)以虚线为对称轴画出①号三角形轴对称图形的另一半。
(3)②号图形的面积是( )平方厘米。(每个小方格的边长为1厘米)
(4)画出②号图形向下平移4格再向右平移3格后的图形。
10.下图中正方形的周长是48厘米,中间有一个长方形,长方形的四个顶点恰好把正方形每边分为两段,其中长的那段是短的长度的2倍,则长方形的面积是多少平方厘米?
11.校园劳动基地的①号地和②号地种小白菜(如图)。小白菜地的面积是多少平方米?写出求面积的具体方法,再计算出结果。【来源:21·世纪·教育·网】
12.一块正方形的花园,它的边长是20米。在花园里横竖各有二条走道,如图,走道宽都是2米。问这块花园种花的面积是多少平方米?
13.如图,一块长方形花圃中间有两条宽度相等的小路(每条小路间距均匀)。这块花圃种花的面积是多少平方米?
14.下图是小娅家和图书馆所在位置的平面图。小娅沿着图中的实线道路,准备从家步行到图书馆。她先走了3分钟,每分钟走84米。21*cnjy*com
(1)小娅家到图书馆的路程共多少米?
(2)小娅还要走多少米才能到达图书馆?
15.将三角形ABC向右平移后得到三角形,如果∠1=45°,∠2=104°,请求出∠3的度数。
16.剪纸是中国古老的民间艺术之一。下面是小明同学剪出的一个花边图形,你能计算出阴影部分的面积吗?
17.学校艺术楼门前要建一个如图所示长12米,宽2米的花坛,如果在花坛边铺一条小路,求小路长多少米?2·1·c·n·j·y
18.按要求完成题目。
(1)算一算:图1的面积是多少?图2的周长是多少?
(2)选词填空:我们是运用( )的方法,通过图形的运动,把不规则的平面图形( )为长方形,使得问题顺利解决。(“平移”“转化”)2-1-c-n-j-y
19.方格图每个小方格边长是1cm。小伍说:“直线l是平行四边形ABCD的对称轴。”小伍说得对吗?请你用轴对称图形的特征说明理由。
20.正六边形作为中国传统形状,象征六合、六顺之意,常被家居配饰所用,如首饰盒、古建的窗户、古井的口、佛塔等等。如图,在古建筑中经常会看到这样的正六边形窗户。
(1)用数学的眼光观察,这个窗户的正六边形外框有( )条对称轴。
(2)请根据已有的经验,探究下面六边形的内角和,并把思考过程用自己喜欢的方式表示出来。(提示:可以画一画、算一算、写一写……)
21.剪纸是中国古老的民间艺术之一。下面是小玲剪的一个花边图形,你能计算出阴影部分的面积吗?
22.求下面图形中阴影部分的面积。
23.按要求完成下面各题。(每个小方格的边长表示1厘米)
(1)根据对称轴补全上面这个轴对称图形。
(2)这个轴对称图形的周长是( )厘米。
(3)画出这个轴对称图形向左平移4格后的图形。
24.按要求完成下面题目。
(1)先从ABCD四个点中任选3个点画一个三角形。这是一个( )三角形。
(2)然后画出三角形向下平移6格后的图形。
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。
(4)画出轴对称图形的另一半。
《(核心素养应用意识)第七单元图形的运动(二)(解决问题)-四年级数学下册人教版》参考答案
1.(1)见详解
(2)4;见详解
【分析】(1)根据题意,从上面看到三竖列,第一竖列有2个小正方形,第二竖列有2个小正方形,第三竖列有1个小正方形,这三竖列上面对齐。【来源:21cnj*y.co*m】
(2)下图中4个位置添上1个小正方形,都能使其成为一个轴对称图形。
【详解】根据分析可知:
(1)先观察,再根据观察的结果作图如下:
(2)如果添上1个小正方形,使刚才画的图形成为一个轴对称图形,共有4种不同的添加方法,其中的一种添法如下:
2.4小时
【分析】根据题意,在镜子中看到的时刻与真实时刻因为对称的,出门前从镜子里看到的钟表时间时针对着9,分钟对着12,是9时,那么实际时间是3时;回来时从镜子里看到的钟表时间时针对着5,分钟对着12,是5时,那么实际时间是7时。经过时间=结束时间-开始时间,12时-从镜子里看到的时间=实际的时间,据此解答。
【详解】根据分析可知:
出门前的时间12-9=3(时)
回来的时间12-5=7(时)
7-3=4(小时)
答:他最少出去了4小时。
3.15平方米
【分析】正方形的面积=边长×边长。由题意得,大正方形的面积是64平方米,因为64=8×8,所以大正方形的边长是8米。小正方形的面积是9平方米,9=3×3,则小正方形的边长是3米。然后再把小正方形平移到上面,则种花的两部分合并成一个长方形(如下图)。
由图可知,长方形的长是8-3=5(米),宽是3米。长方形的面积=长×宽,直接将数据代入即可算出种花的面积。
【详解】64=8×8,则大正方形的边长是8米。
9=3×3,则小正方形的边长是3米。
(8-3)×3
=5×3
=15(平方米)
答:李奶奶家种花的面积是15平方米。
4.(1)见详解;(2)12
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)图中每格是边长1厘米的正方形面积是1平方厘米,数出有几个整格,再数出有几个半格,2个半格合成1个整格,再相加即为轴对称图形的面积。www-2-1-cnjy-com
【详解】(1)如图:
(2)10个整格,4个半格是4÷2=2(个)整格,合起来是10+2=12(个)
即这个轴对称图形的面积是12平方厘米。
5.48平方厘米
【分析】把横条向下平移到下边,把竖条向左平移到左边,这时空白部分是一整块长方形,长是(10-2)厘米,宽是(8-2)厘米,根据长方形面积=长×宽,带入数值即可解答。
【详解】(10-2)×(8-2)
=8×6
=48(平方厘米)
答:空白部分的面积是48平方厘米。
6.144平方厘米
【分析】如果求一道纸条的面积,比较好求,20×2=40(平方厘米),但是其中有多个交叉重叠部分,直接求解有一定难度,这时可以通过平移,将横向纸条向上或向下平移,将纵向纸条向左或右平移,形成如图形。www.21-cn-jy.com
中间白色部分是一个边长为20-2×2=20-4=16厘米的正方形,用大正方形的面积减去白色部分的面积,就是“井”字部分的面积。
【详解】20×20-(20-2×2)×(20-2×2)
=20×20-(20-4)×(20-4)
=20×20-16×16
=400-256
=144(平方厘米)。
答:“井”字部分的面积是144平方厘米。
7.见详解
【分析】先要观察图中的两种食物,一种是熊猫喜欢吃的竹子,另一种是小狗喜欢吃的骨头。然后把相对应的动物和食物的位置作比较,判断出平移的方向和距离。
【详解】熊猫先向右平移3格,再向上平移5格(或先向上平移5格,再向右平移3格)就可以吃到竹子;小狗先向下平移4格,再向右平移5格(或先向右平移5格,再向下平移4格)就可以吃到骨头。
8.64平方米
【分析】通过平移,将图形变为如下图:
据此可知,小路的面积相当于长方形草坪的面积减去长为(20-2)米、宽为(14-2)米的长方形面积;根据长方形的面积=长×宽,代入数据解答。
【详解】20×14-(20-2)×(14-2)
=20×14-18×12
=280-216
=64(平方米)
答:小路的占地面积是64平方米。
9.(1)(2)(4)图见详解
(3)6
【分析】(1)根据三角形高的意义,延长三角形ABC的边AB到D,再根据过直线外一点画已知直线的垂线的方法,从点C向AB的延长线画垂线段,与其交于点E,CE就是AB边上的高,由此作图即可;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可;
(3)通过平移可知,②号图形的面积等于长3厘米、宽2厘米的长方形的面积,长方形的面积=长×宽,依此计算;
(4)根据平移的特征,把②号图形的各顶点分别向下平移4格,再向右平移3格,依次连接即可得到平移后的图形。
【详解】(1)(2)(4)作图如下:
(3)3×2=6(平方厘米)
②号图形的面积是6平方厘米。
10.64平方厘米
【分析】根据正方形的周长÷4=边长,代入数据即可求出正方形的边长,因为长的那段是短的长度的2倍。所以正方形的边长是短的长度的(2+1)倍,据此用除法求出短的长度,再用减法求出长的部分的长度;长方形的面积相当于正方形的面积减去4个三角形的面积和,4个三角形通过拼接可以拼成2个正方形,其中1个边长等于短的长度,另一个边长等于长的部分的长度,根据正方形的面积=边长×边长,分别求出2个正方形的面积,再求出它们的和;进而求出大正方形的面积,然后用减法即可求出长方形的面积。
【详解】边长:48÷4=12(厘米)
短:12÷(2+1)
=12÷3
=4(厘米)
长:12-4=8(厘米)
三角形:4×4+8×8
=16+64
=80(平方厘米)
大正方形:12×12=144(平方厘米)
长方形:144-80=64(平方厘米)
答:长方形的面积是64平方厘米。
【点睛】本题考查了平面图形的知识的应用,掌握相关的公式以及转化、平移等解题技巧是解答本题的关键。
11.24平方米;把①号地向右平移1个格后,①号地与②号地拼成一个长6米,宽4米的长方形
【分析】如图:
根据题意,两个点之间的距离是1米,把①号地向右平移1个格后,①号地与②号地拼成一个长6米,宽4米的长方形,根据长方形的面积=长×宽,解答即可。
【详解】把①号地向右平移1个格后,①号地与②号地拼成一个长6米,宽4米的长方形。
6×4=24(平方米)
答:小白菜地的面积是24平方米。
12.256平方米
【分析】这个正方形的花园里横竖各有二条宽都是2米走道,把4条走道平移到花园的边上,中间部分就为种花的部分。由图可知中间种花的部分为一个正方形,正方形的边长为花园的边长减去2个走道的宽,根据正方形的面积公式:正方形面积=边长×边长,求出种花的面积。21·世纪*教育网
【详解】20-2×2
=20-4
=16(米)
16×16=256(平方米)
答:这块花园种花的面积是256平方米。
13.1620平方米
【分析】由题意得,长方形花圃的长是56米,宽是30米。它的中间有两条宽度相等的小路且每条小路的间距为1米,两条小路将长方形分成了三部分。如果将两边的部分向中间平移,那么这个花圃就组成了一个新的长方形。这个长方形的长是(56-1-1)米,宽是30米。长方形的面积=长×宽,直接将数据代入即可算出这块花圃种花的面积。
【详解】(56-1-1)×30
=(55-1)×30
=54×30
=1620(平方米)
答:这块花圃种花的面积是1620平方米。
14.(1)656米
(2)404米
【分析】(1)从图中可以看出,从小娅家到图书馆的路线通过平移,可转变为一条宽和一条长,所以求出图中长加宽的和就是小娅家到图书馆的路程。21*cnjy*com
(2)已知小娅先走了3分钟,每分钟走84米,根据速度×时间=路程,可以求出先走了的路程,即(84×3)米,再用总路程减走了的路程,即得到还要走的路程。据此解答。
【详解】(1)206+450=656(米)
答:小娅家到图书馆的路程共656米。
(2)656-3×84
=656-252
=404(米)
答:小娅还要走404米才能到达图书馆。
15.31°
【分析】由题意得,将三角形ABC向右平移后得到三角形,∠1=45°,所以=45°。∠2、∠3和组成了一个平角,求∠3的度数,直接用180°减去∠2再减去的度数即可解答。【版权所有:21教育】
【详解】∠3=180°-104°-45°
=76°-45°
=31°
答:∠3的度数是31°。
16.12平方厘米
【分析】由图可知,每两个正方形中的阴影部分合起来可以组成一个完整的正方形,整个图中的阴影部分可以组成三个完整的正方形。正方形的面积=边长×边长,可以先用2乘2算出一个正方形的面积,再乘3即可算出三个正方形的面积是多少平方厘米。
【详解】2×2×3=4×3=12(平方厘米)
答:阴影部分的面积是12平方厘米。
17.28米
【分析】把各不规则部分的横线段和竖线段进行平移,可得到所求周长恰好是长为12米,宽为2米的长方形的周长,用(长+宽)×2,即可求出小路长。21cnjy.com
【详解】(12+2)×2
=14×2
=28(米)
答:小路长28米。
【点睛】此题主要考查学生对矩形两组对边对应相等的性质的掌握情况,做这类题时还需注意利用平移的思想。
18.(1)图1的面积是20平方厘米,图2的周长是18厘米。
(2)平移;转化
【分析】(1)图1是不规则图形,但通过观察发现这是一个上下对称的轴对称图形,可以利用平移的方法将其变成规则图形后求面积。图2的周长也可以用平移的方法将其转化成长方形后再求其周长。21世纪教育网版权所有
(2)根据(1)中的思路来选词进行填空即可。
【详解】(1)如图,将图形用虚线进行分割,将虚线右边图形向左进行平移5格后,便组成了一个长为5厘米,宽为4厘米的长方形。根据长方形面积=长×宽,可知该图形面积=5×4=20(平方厘米)
如图,将该图形的横向线段分别向上进行平移,纵向线段分别向右平移后,该图形就变成了一个长是5厘米,宽是4厘米的长方形,根据长方形的周长=(长+宽)×2可知,该图形周长=(5+4)×2=9×2=18(厘米)
答:图1的面积是20平方厘米,图2的周长是18厘米。
(2)根据(1)的方法可知,我们是运用平移的方法,通过图形的运动,把不规则的平面图形转化为长方形,使得问题顺利解决。
19.小伍说得不对;因为点和点到直线的距离不相等。
【分析】轴对称图形的特点是:如果一个图形沿某条直线对折后,能够与自身完全重合,那么这个图形就是轴对称图形,这条直线就是对称轴。对于平行四边形来说,只有当它是特殊的平行四边形(如矩形或菱形)时,才可能有对称轴。一般的平行四边形没有对称轴,因此直线l不可能是平行四边形ABCD的对称轴。
【详解】根据分析得:小伍说得不对;因为点D和点C到直线l的距离不相等。
20.(1)6
(2)720°
【分析】(1)这个六边形窗户的外框是轴对称图形,找出它的对称轴,要使对称轴左右两边的图形完全相同。可分别过这个六边形窗户的外框的两个相对的顶点,或过这个六边形窗户的外框的两个相对的边的中点,画出它的对称轴;
(2)一个三角形的内角和为180°,正六边形可被分成4个三角形,用180°×4,即可得到这个正六边形的内角和是多少度。
【详解】(1)过这个六边形窗户的外框的两个相对的顶点,可画出它的对称轴,这样的对称轴有3条;过这个六边形窗户的外框的两个相对的边的中点,可画出它的对称轴,这样的对称轴有3条。因此这个六边形窗户的外框共有6条对称轴。
(2)180×4=720°
因此这个正六边形的内角和是720°。
21.16平方厘米
【分析】通过观察图形可知,阴影部分的面积可以通过平移“转化”为边长是2厘米的4个正方形的面积。根据正方形的面积=边长×边长,把数据代入公式,即可解题。
【详解】由分析可知:
2×2×4
=4×4
=16(平方厘米)
答:阴影部分的面积是16平方厘米。
22.12平方分米
【分析】观察图片可以发现相邻两个图形,阴影部分通过平移可以组成一个完整的正方形,相邻图形的两两组合,可以组成三个正方形,正方形的面积=边长×边长,求出一个正方形面积再乘3即为所求。21教育网
【详解】2×2×3
=4×3
=12(平方分米)
答:图形中阴影部分的面积是12平方分米。
23.(1)(3)见详解
(2)12
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴虚线的下边画出上半图的关键对称点,依次连接即可。
(2)由图可知,这个图形的一周有12个小方格的边长,所以它的周长是12厘米。
(3)根据平移的特征,把这个轴对称图形的各顶点分别向左平移4格,依次连接即可得到平移后的图形。
【详解】(1)(3)如图
;
(2)这个轴对称图形的周长是12厘米。
24.(1)图见详解;等腰;
(2)(3)(4)见详解
【分析】(1)先从ABCD四个点中任选3个点画一个三角形(画法不唯一),等腰三角形的两腰相等,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底,依此画图。21·cn·jy·com
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
(3)根据三角形高的意义,在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高,再根据过直线外一点画已知条直线的垂线的方法,由此作图即可。【出处:21教育名师】
(4)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)先从ABCD四个点中任选3个点画一个三角形。如图:
这是一个等腰三角形。
(2)然后画出三角形向下平移6格后的图形。如图:
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。如图:
(4)画出轴对称图形的另一半。如图:
(三角形画法不唯一)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
