2024-2025年人教版五年级下册数学期末提升训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学期末提升训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 300.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 05:03:13 | ||
图片预览



文档简介
2024-2025年人教版五年级下册数学期末提升训练
一、选择题
1.的分子加上12,要使分数的大小不变,分母应该( )。
A.加上12 B.乘3 C.乘4 D.乘12
2.三瓶同样的饮料,小星喝了一瓶的,小月喝了一瓶的,小林喝了一瓶的。他们三个人( )剩下的饮料最多。
A.小星 B.小月 C.小林 D.无法判断
3.有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称( )次才能保证找到次品。
A.3 B.4 C.5 D.6
4.如图的长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的( )。
A. B. C. D.
5.把一张长72cm,宽60cm的长方形纸,裁成同样大小、面积尽可能大的正方形纸,且纸无剩余,至少能裁( )张。
A.2 B.4 C.30 D.6
二、填空题
6.( )÷15=0.6==15÷( )。
7.的分数单位是( ),再加上( )个这样的分数单位就是最小的质数。
8.在2,5,0,8四个数字中任选三个组成的有因数3的最大数是( );同时是2,5的倍数的最小的数是( );2,3的公倍数有( )。
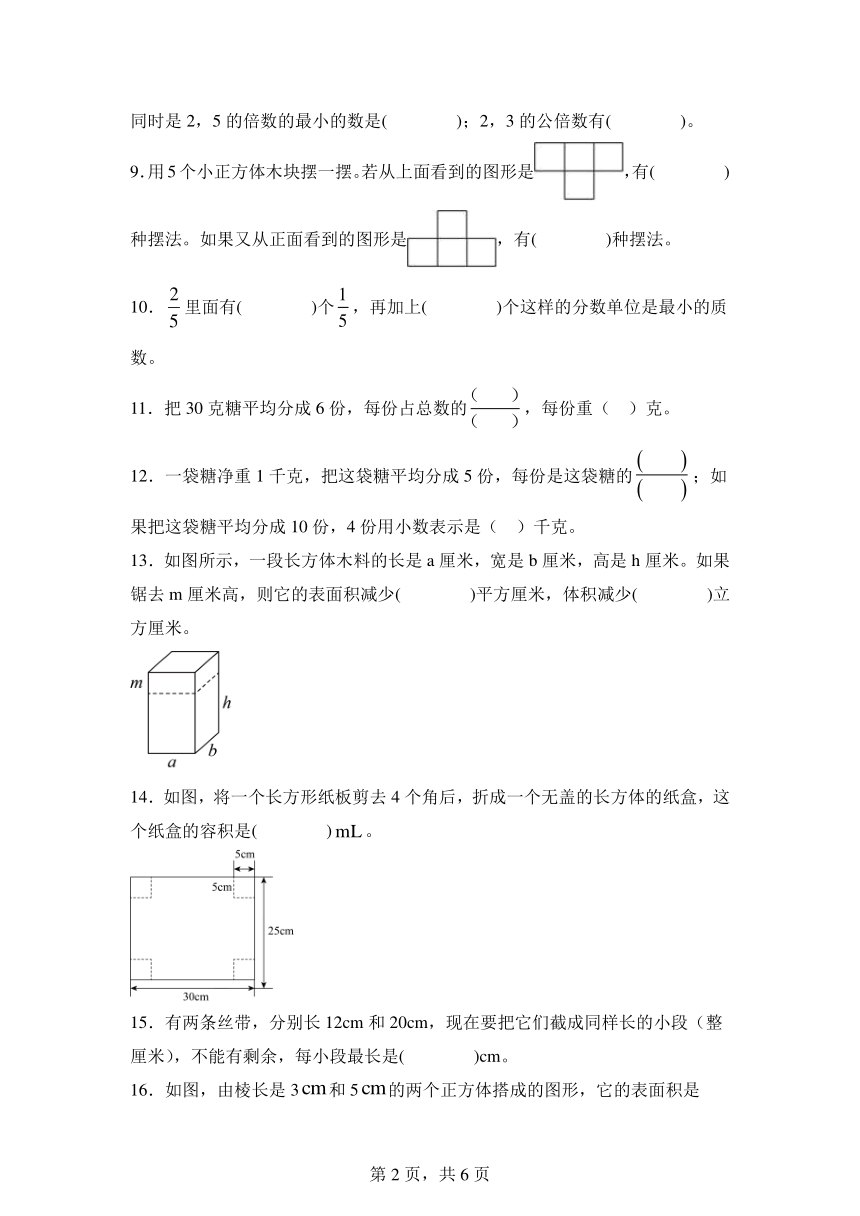
9.用5个小正方体木块摆一摆。若从上面看到的图形是,有( )种摆法。如果又从正面看到的图形是,有( )种摆法。
10.里面有( )个,再加上( )个这样的分数单位是最小的质数。
11.把30克糖平均分成6份,每份占总数的,每份重( )克。
12.一袋糖净重1千克,把这袋糖平均分成5份,每份是这袋糖的;如果把这袋糖平均分成10份,4份用小数表示是( )千克。
13.如图所示,一段长方体木料的长是a厘米,宽是b厘米,高是h厘米。如果锯去m厘米高,则它的表面积减少( )平方厘米,体积减少( )立方厘米。
14.如图,将一个长方形纸板剪去4个角后,折成一个无盖的长方体的纸盒,这个纸盒的容积是( )。
15.有两条丝带,分别长12cm和20cm,现在要把它们截成同样长的小段(整厘米),不能有剩余,每小段最长是( )cm。
16.如图,由棱长是3和5的两个正方体搭成的图形,它的表面积是( ),体积是( )。
17.如果a÷b=20(a、b均为非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
三、判断题
18.任何两个质数的和都是偶数。( )
19.2+3=5,2+5=7,所以两个质数的和一定是奇数。( )
20.淘气和笑笑各自拿出自己压岁钱的捐给灾区,他们所捐的钱数是相等的。( )
21.三个连续偶数的和一定是6的倍数。( )
22.一根3米长的铁丝,切下米后,还剩下2米。( )
四、计算题
23.直接写出得数。
3.6+0.7= 4-0.4= 2.4×0.3= 0.48÷0.6=
24.计算下列各题,能简算的要简算。
+- +-+ 7×1.25×8
25.解方程。
+x= -x= 2x-97=34.2
26.求下面图形的表面积和体积。
五、解答题
27.某学校暑假期间安排王老师每4天值一次班,李老师每6天值一次班,张老师每8天值一次班,如果7月1日他们三人同一天值班,下一次他们三人同一天值班是几月几日?
28.一个长方体的底面是一个周长为30厘米的长方形,高为10厘米。如果长和宽的厘米数都是合数,那么这个长方体的棱长和、表面积和体积分别是多少?
29.五(3)班同学上体育课时,每行站3人,最后一行少2人;每行站6人,最后一行少5人;每行站5人,结果最后一行只有1人。五(3)班最少有多少人?
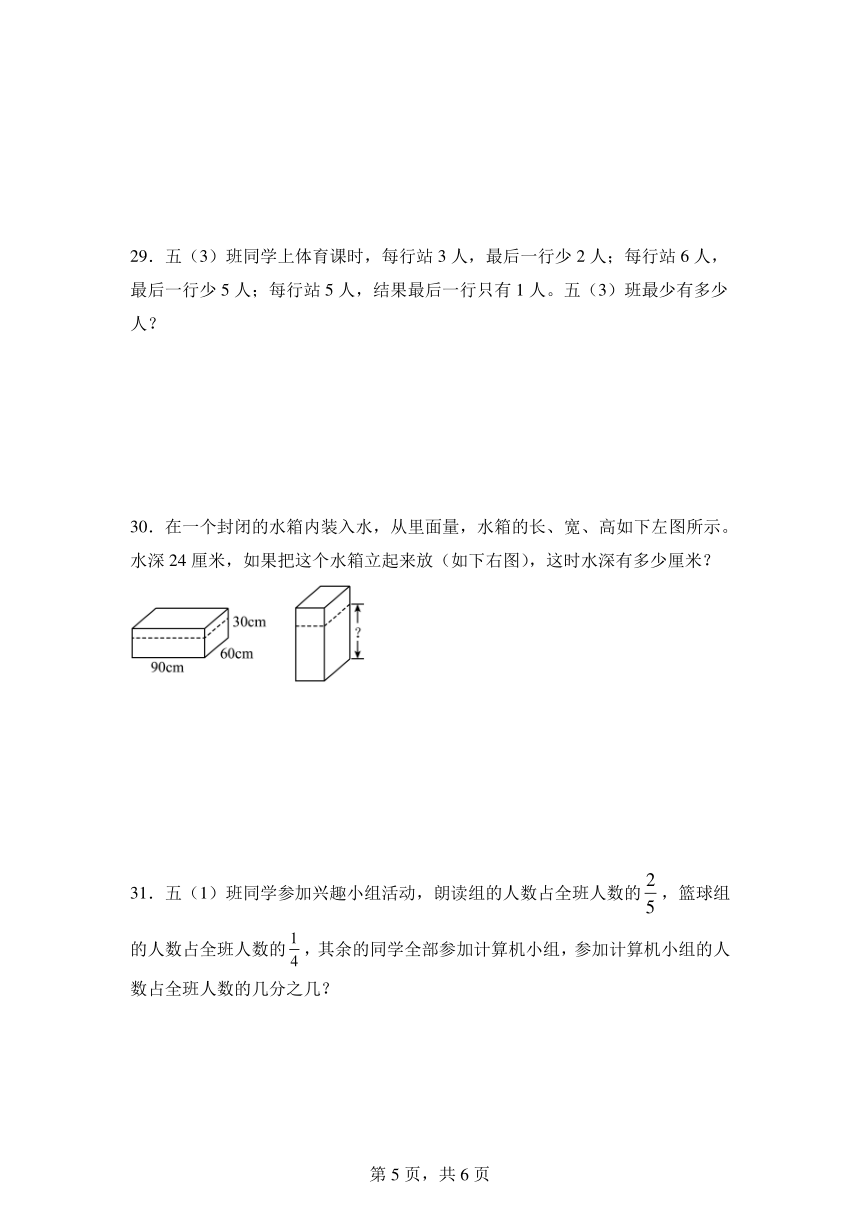
30.在一个封闭的水箱内装入水,从里面量,水箱的长、宽、高如下左图所示。水深24厘米,如果把这个水箱立起来放(如下右图),这时水深有多少厘米?
31.五(1)班同学参加兴趣小组活动,朗读组的人数占全班人数的,篮球组的人数占全班人数的,其余的同学全部参加计算机小组,参加计算机小组的人数占全班人数的几分之几?
32.学校放学时,小夏直接走路回家,行程情况统计如下图所示。到家后,小夏倒了一杯纯牛奶,先喝了整杯的,再开始做语文作业,用了小时完成;休息了一会儿,他发现牛奶凉了,就兑满了热水,又喝了半杯后,开始写数学作业,结果比完成语文作业少用了小时。然后,他就愉快地出去玩了。
(1)小夏回家途中的休息时间占路上总时间的几分之几?
(2)小夏回家做作业一共用了多少小时?
(3)在这整个过程中,小夏一共喝了多少杯纯牛奶?
第6页,共6页
第5页,共6页
《2024-2025年人教版五年级下册数学期末提升训练》参考答案
1.C
【分析】分数的基本性质:分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此先算出分子加上12相当于给分子乘几,则分母也要乘相同的数,据此解答。
【详解】4+12=16
16÷4=4
7×4=28
=
的分子加上12,要使分数的大小不变,分母应该乘4。
故答案为:C
2.A
【分析】分数的大小比较:分母相同的分数,分子大的分数大;分子相同的分数,分母小的分数大;分母不同的分数,先通分再比较。根据题意,三瓶同样的饮料,先比较谁喝的最少,那么他剩下的饮料最多。
【详解】
小星喝的最少,所以他剩下的饮料最多。
故答案为:A
3.A
【分析】将16个零件分成三组(5,5,6),先把两组5个放在天平两侧,若平衡,次品在剩余6个零件中;若不平衡,次品在较轻的5个中。
若次品在剩余6个零件中,将6个零件分成三组(2,2,2),先把两组2个放在天平两侧,若平衡,则次品在剩余2个中,若不平衡,次品在较轻的一组中;再把次品的一组放在天平两次,较轻的一边为次品;
若次品在第一次称的5个零件中,把5个零件分成(2,2,1)三组,把两组2个放在天平两侧,若平衡,剩下的为次品,若不平衡,次品在较轻的一侧;再把较轻的一侧的2个零件放在天平两侧,即可测出次品零件;至少需要3次才能保证找出次品。
【详解】根据分析可知,有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称3次才能保证找到次品。
故答案为:A
4.C
【分析】设小正方形边长为1,求出长方形面积;阴影部分面积为两个三角形面积;根据三角形面积公式:面积=底×高÷2,据此求出阴影部分面积,再用阴影部分面积÷长方形面积,即可解答。
【详解】假设小正方形边长为1。
长方形面积:
1×1×5
=1×5
=5
阴影部分面积:
1×1÷2+1×1÷2
=1÷2+1÷2
=0.5+0.5
=1
1÷5=
长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的。
故答案为:C
5.C
【分析】把一块长方形纸裁成同样大小、面积尽可能大的正方形,且没有剩余,说明正方形的边长是长、宽的最大公因数,把72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数,即是正方形的最大边长。再看长、宽里面分别有几个这样的最大公因数,最后相乘,即可求出至少能裁的张数。
【详解】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即正方形的边长最大是12cm。
72÷12=6(张)
60÷12=5(张)
一共:6×5=30(张)
至少能裁30张。
故答案为:C
6. 9;;25
【分析】小数化分数:一位小数、两位小数、三位小数 化为分数后,分数的分母为10、100、1000 把原来的小数去掉小数点作分子;化成分数后,能约分的要约分;分数的分子相当于被除数,分母相当于除数,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此先将小数化成分数,再根据分数与除法的关系,以及它们通用的基本性质进行填空。
【详解】0.6==;15÷5×3=9;15÷3×5=25
9÷15=0.6==15÷25
7. 10
【分析】判定一个分数的单位看分母,分母是几,分数单位就是几分之一;最小的质数是2,用2减去原分数求出差,再看有几个这样的分数单位即可。
【详解】的分数单位是,最小的质数是2。
,里有10个。
因此的分数单位是,再加上10个这样的分数单位就是最小的质数。
8. 852 250 852,582,528,258
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
从题意可知:在2,5,0,8四个数字中选取3个数字,且数字和是3的倍数的只有2,5,8。即2+5+8=18,将2,5,8三个数字从大到小排列,即可组成的有因数3的最大数。将2,5,8三个数字组成的3的倍数中,个位上是2或8,这个就是2,3的公倍数。
同时是2,5的倍数的个位上的数字一定是0,与较小的2和5组成最小的数即可。
【详解】在2,5,0,8四个数字中任选三个组成的有因数3的最大数是852;同时是2,5的倍数的最小的数是250;2,3的公倍数有852,582,528,258。
9. 4 2
【分析】根据从上面看到的图形可以判断,下层4个小正方体是固定的,第5个小正方体可以在任意一个小正方体上面,所以共4种;根据又从正面看到的图形可以判断,第5个小正方体只能在中间两个小正方体上面,所以共2种。
【详解】
用5个小正方体木块摆,若从上面看到的图形是,有,有4种摆法。如果又从正面看到的图形是,有,有2种摆法。
10. 2 8
【分析】把单位“1”平均分成若干份,取一份的数,叫做分数单位,分数的分子是几,里面就有几个这样的分数单位;在自然数中,除了1和它本身外,没有别的因数的数为质数,据此解题即可。
【详解】2=
10-2=8
所以里面有2个,再加上8个这样的分数单位是最小的质数。
11.;5
【分析】分析题目,把30克糖看作单位“1”,用1除以分成的份数即可得到每份占总数的几分之几;再用30除以分成的份数即可得到每份重多少克。
【详解】1÷6=
30÷6=5(克)
把30克糖平均分成6份,每份占总数的,每份重5克。
12.;0.4
【分析】把这袋糖的总质量看作单位“1”,平均分成5份,用1除以5,求出每份是这袋糖的几分之几;
如果把1千克的糖平均分成10份,用这袋糖的总质量除以10,求出一份是多少千克,再乘4,即是4份是多少千克,结果用小数表示。
【详解】1÷5=
1÷10×4
=0.1×4
=0.4(千克)
一袋糖净重1千克,把这袋糖平均分成5份,每份是这袋糖的();如果把这袋糖平均分成10份,4份用小数表示是(0.4)千克。
13. 2am+2bm abm
【分析】根据题意,一段长方体木料锯去m厘米高,则减少的表面积是4个侧面的面积,即2个长为a厘米、宽为m厘米的长方形的面积与2个长为b厘米、宽为m厘米的长方形的面积之和;根据“长方形的面积=长×宽”求出减少的表面积;
减少的体积是长为a厘米、宽为b厘米、高为m厘米的长方体的体积;根据“长方体的体积=长×宽×高”求出减少的体积。
【详解】a×m×2+b×m×2=(2am+2bm)(平方厘米)
a×b×m=abm(立方厘米)
填空如下:
则它的表面积减少(2am+2bm)平方厘米,体积减少(abm)立方厘米。
14.1500
【分析】根据题意可知,折成长方体后,长方体的长是(30-5×2)cm,宽是(25-5×2)cm,高是5cm;根据长方体容积=长×宽×高,代入数据,即可解答。
【详解】(30-5×2)×(25-5×2)×5
=(30-10)×(25-10)×5
=20×15×5
=300×5
=1500(cm3)
1500cm3=1500mL
这个纸盒的容积是1500。
15.4
【分析】求每小段丝带最长是多少厘米,即求12和20的最大公因数,先把12和20进行分解质因数,这两个数的公有质因数的乘积就是这两个数的最大公因数,据此解答。
【详解】12=2×2×3,20=2×2×5,12和20的最大公因数是2×2=4。
有两条丝带,分别长12cm和20cm,现在要把它们截成同样长的小段(整厘米),不能有剩余,每小段最长是4cm。
16. 186 152
【分析】通过平移,将小正方体上面的面平移到下面,它的表面积=大正方体的表面积+小正方体1个面的面积×4,正方体表面积=棱长×棱长×6;它的体积=大正方体的体积+小正方体的体积,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】5×5×6+3×3×4
=150+36
=186()
5×5×5+3×3×3
=125+27
=152()
它的表面积是186,体积是152。
17.b a
【分析】如果两个数是倍数关系,那么它们的最大公因数是两个数中的较小数,最小公倍数是两个数中的较大数,据此解答。
【详解】如果a÷b=20(a、b均为非0自然数),那么a是b的倍数,a>b,所以a和b的最大公因数是b,最小公倍数是a
18.×
【分析】只有1和它本身两个因数的数是质数;能被2整除的数是偶数;据此举例判断即可。
【详解】2和3都是质数,2+3=5,5是奇数不是偶数;原题说法错误。
故答案为:×
19.×
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数;整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;举例说明。
【详解】例如:3和5是质数
3+5=8,8是偶数
5和7是质数
5+7=12,12是偶数
所以两个质数的和不一定是奇数,原题说法错误。
故答案为:×
20.×
【分析】分数的意义:将一个整体平均分成若干份,其中的一份或几份可以用分数表示。表示将整体平均分成5份,取其中的2份。据此解题。
【详解】淘气和笑笑各有多少压岁钱不明确,那么淘气压岁钱的和笑笑压岁钱的不一定相等,那么他们所捐的钱数是不一定相等的。
故答案为:×
21.√
【分析】可以用字母表示中间数为2a,根据偶数的特征分别表示出3个偶数,比它小的偶数是2a-2,比它大的偶数是2a+2,再相加计算即可。
【详解】2a-2+2a+2a+2=6a
6a是6的倍数,所以原题说法正确。
故答案为:√
22.×
【分析】切下米,分数后面加单位表示具体的长度,用总长度减去切下去的长度即可求出还剩下的长度。
【详解】3-=(米)
还剩下米,原题说法错误。
故答案为:×
23.4.3;3.6;0.72;0.8
;;;2
【详解】略
24.;;70
【分析】(1)按照从左往右的顺序依次计算;
(2)根据加法交换律和结合律把原式写成(-)+(+),再进一步计算即可;
(3)根据乘法结合律先算1.25×8,再和7相乘即可。
【详解】+-
=+-
=-
=
+-+
=(-)+(+)
=+1
=
7×1.25×8
=7×(1.25×8)
=7×10
=70
25.x=;x=;x=65.6
【分析】(1)根据等式的基本性质,方程两边同时减去即可;
(2)根据减数=被减数-差可知x=-,进一步解方程即可;
(3)根据等式的基本性质,方程两边先同时加上97,再同时除以2即可。
【详解】+x=
解:x=-
x=-
x=
-x=
解:x=-
x=-
x=
2x-97=34.2
解:2x=34.2+97
2x=131.2
x=131.2÷2
x=65.6
26.表面积是912dm2,体积是1472dm3
【分析】通过观察可知,这个立体图形的表面积相当于一个长为20dm、宽为8dm、高为6dm的长方体表面积加上一个棱长为8dm的正方体4个面的面积;这个立体图形的体积相当于一个长为20dm、宽为8dm、高为6dm的长方体体积加上一个棱长为8dm的正方体体积;根据长方体的表面积=(长×宽+长×高+宽×高)×2、正方体的表面积=棱长×棱长×6、正方体的体积=棱长×棱长×棱长、长方体的体积=长×宽×高 代入数据即可解答。
【详解】表面积:(20×8+20×6+8×6)×2+8×8×4
=(160+120+48)×2+8×8×4
=328×2+8×8×4
=656+256
=912(dm2)
体积:20×8×6+8×8×8
=960+512
=1472(dm3)
这个立体图形的表面积是912dm2,体积是1472dm3。
27.7月25日
【分析】根据题意,王老师每4天值一次班,李老师每6天值一次班,张老师每8天值一次班,那么他们三人同一天值班的间隔天数就是4、6和8的公倍数;先求出4、6和8的最小公倍数,再加上第一次三人同时值班的日期,即是下一次他们三人同一天值班的日期。
【详解】4=2×2
6=2×3
8=2×2×2
4、6和8的最小公倍数:2×2×2×3=24
即每24天三人同一天值班。
7月1日+24天=7月25日
答:下一次他们三人同一天值班是7月25日。
28.棱长和是100厘米,表面积是408平方厘米,体积是540立方厘米
【分析】根据长方体的底面周长=(长+宽)×2,可知长、宽的和是(30÷2)厘米,即15厘米,因为长和宽的厘米数都是合数,一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数,据此将15拆分为2个合数相加,即6+9;再根据长方体棱长和=(长+宽+高)×4、长方体的表面积=(长×宽+长×高+宽×高)×2、长方体的体积=长×宽×高,代入数据即可求出这个长方体的棱长和、表面积和体积。
【详解】30÷2=15(厘米)
15=6+9
长为9厘米,宽为6厘米,
棱长和:(9+6+10)×4
=25×4
=100(厘米)
表面积:(9×6+9×10+6×10)×2
=(54+90+60)×2
=204×2
=408(平方厘米)
体积:9×6×10=540(立方厘米)
答:这个长方体的棱长和是100厘米,表面积是408平方厘米,体积是540立方厘米。
29.31人
【分析】每行站3人,最后一行少2人,说明这种情况下最后一行只有1人。每行站6人,最后一行少5人,说明这种情况下最后一行也只有1人。又由于每行站5人,结果最后一行只有1人。那么将多的这1人先不考虑,其他的人数就是3、5、6的最小公倍数。5和6互质,这两个数的乘积就是它们的最小公倍数,由于6是3的倍数,所以5和6的最小公倍数也会是3、5、6的最小公倍数。将最小公倍数加1,求出五(3)班最少有多少人。
【详解】5×6+1
=30+1
=31(人)
答:五(3)班最少有31人。
30.72厘米
【分析】根据长方体体积公式:体积=长×宽×高,代入数据,求出左图形里水深24厘米的水的体积,由于体积不变,再用水的体积÷(右图的长×宽),即可求出这时水深,据此解答。
【详解】90×60×24÷(60×30)
=90×60×24÷1800
=5400×24÷1800
=129600÷1800
=72(厘米)
答:这时水深72厘米。
31.
【分析】将全班总人数看作单位“1”。 朗读组的人数占全班人数的,篮球组的人数占全班人数的,两组一共占全班人数的(+),用1减去(+)即可求出参加计算机小组的人数占全班人数的几分之几。
【详解】1-(+)
=1-(+)
=1-
=
答:参加计算机小组的人数占全班人数的。
32.(1);
(2)小时;
(3)杯
【分析】(1)根据统计图可知,小夏休息时间用了(15-5)分钟,总时间是25分钟;用小夏休息时间除以总时间,即可求出小夏回家途中的休息时间占路上总时间的分率;
(2)用小夏完成语文作业的时间-小时,求出小夏完成数学作业的时间,再加上完成语文作业时间,即可求出小夏回家做作业一共用时间;
(3)把这杯牛奶的总量看作单位“1”,先喝了整杯的,即喝了杯;用1-=杯,求出剩下牛奶的量,他发现牛奶凉了,就兑满了热水,又喝了半杯,实际上喝了杯的一半,杯的一半是杯,用先喝的杯再加上杯,即可求出小夏一共喝了多少杯纯牛奶。
【详解】(1)(15-5)÷25
=10÷25
=
答:小夏回家途中的休息时间占路上总时间的。
(2)-+
=-+
=+
=(小时)
答:小夏回家做作业一共用了小时。
(3)1-=(杯)
杯的一半是杯。
+=(杯)
答:小夏一共喝了杯。
答案第14页,共15页
答案第15页,共15页
一、选择题
1.的分子加上12,要使分数的大小不变,分母应该( )。
A.加上12 B.乘3 C.乘4 D.乘12
2.三瓶同样的饮料,小星喝了一瓶的,小月喝了一瓶的,小林喝了一瓶的。他们三个人( )剩下的饮料最多。
A.小星 B.小月 C.小林 D.无法判断
3.有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称( )次才能保证找到次品。
A.3 B.4 C.5 D.6
4.如图的长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的( )。
A. B. C. D.
5.把一张长72cm,宽60cm的长方形纸,裁成同样大小、面积尽可能大的正方形纸,且纸无剩余,至少能裁( )张。
A.2 B.4 C.30 D.6
二、填空题
6.( )÷15=0.6==15÷( )。
7.的分数单位是( ),再加上( )个这样的分数单位就是最小的质数。
8.在2,5,0,8四个数字中任选三个组成的有因数3的最大数是( );同时是2,5的倍数的最小的数是( );2,3的公倍数有( )。
9.用5个小正方体木块摆一摆。若从上面看到的图形是,有( )种摆法。如果又从正面看到的图形是,有( )种摆法。
10.里面有( )个,再加上( )个这样的分数单位是最小的质数。
11.把30克糖平均分成6份,每份占总数的,每份重( )克。
12.一袋糖净重1千克,把这袋糖平均分成5份,每份是这袋糖的;如果把这袋糖平均分成10份,4份用小数表示是( )千克。
13.如图所示,一段长方体木料的长是a厘米,宽是b厘米,高是h厘米。如果锯去m厘米高,则它的表面积减少( )平方厘米,体积减少( )立方厘米。
14.如图,将一个长方形纸板剪去4个角后,折成一个无盖的长方体的纸盒,这个纸盒的容积是( )。
15.有两条丝带,分别长12cm和20cm,现在要把它们截成同样长的小段(整厘米),不能有剩余,每小段最长是( )cm。
16.如图,由棱长是3和5的两个正方体搭成的图形,它的表面积是( ),体积是( )。
17.如果a÷b=20(a、b均为非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
三、判断题
18.任何两个质数的和都是偶数。( )
19.2+3=5,2+5=7,所以两个质数的和一定是奇数。( )
20.淘气和笑笑各自拿出自己压岁钱的捐给灾区,他们所捐的钱数是相等的。( )
21.三个连续偶数的和一定是6的倍数。( )
22.一根3米长的铁丝,切下米后,还剩下2米。( )
四、计算题
23.直接写出得数。
3.6+0.7= 4-0.4= 2.4×0.3= 0.48÷0.6=
24.计算下列各题,能简算的要简算。
+- +-+ 7×1.25×8
25.解方程。
+x= -x= 2x-97=34.2
26.求下面图形的表面积和体积。
五、解答题
27.某学校暑假期间安排王老师每4天值一次班,李老师每6天值一次班,张老师每8天值一次班,如果7月1日他们三人同一天值班,下一次他们三人同一天值班是几月几日?
28.一个长方体的底面是一个周长为30厘米的长方形,高为10厘米。如果长和宽的厘米数都是合数,那么这个长方体的棱长和、表面积和体积分别是多少?
29.五(3)班同学上体育课时,每行站3人,最后一行少2人;每行站6人,最后一行少5人;每行站5人,结果最后一行只有1人。五(3)班最少有多少人?
30.在一个封闭的水箱内装入水,从里面量,水箱的长、宽、高如下左图所示。水深24厘米,如果把这个水箱立起来放(如下右图),这时水深有多少厘米?
31.五(1)班同学参加兴趣小组活动,朗读组的人数占全班人数的,篮球组的人数占全班人数的,其余的同学全部参加计算机小组,参加计算机小组的人数占全班人数的几分之几?
32.学校放学时,小夏直接走路回家,行程情况统计如下图所示。到家后,小夏倒了一杯纯牛奶,先喝了整杯的,再开始做语文作业,用了小时完成;休息了一会儿,他发现牛奶凉了,就兑满了热水,又喝了半杯后,开始写数学作业,结果比完成语文作业少用了小时。然后,他就愉快地出去玩了。
(1)小夏回家途中的休息时间占路上总时间的几分之几?
(2)小夏回家做作业一共用了多少小时?
(3)在这整个过程中,小夏一共喝了多少杯纯牛奶?
第6页,共6页
第5页,共6页
《2024-2025年人教版五年级下册数学期末提升训练》参考答案
1.C
【分析】分数的基本性质:分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此先算出分子加上12相当于给分子乘几,则分母也要乘相同的数,据此解答。
【详解】4+12=16
16÷4=4
7×4=28
=
的分子加上12,要使分数的大小不变,分母应该乘4。
故答案为:C
2.A
【分析】分数的大小比较:分母相同的分数,分子大的分数大;分子相同的分数,分母小的分数大;分母不同的分数,先通分再比较。根据题意,三瓶同样的饮料,先比较谁喝的最少,那么他剩下的饮料最多。
【详解】
小星喝的最少,所以他剩下的饮料最多。
故答案为:A
3.A
【分析】将16个零件分成三组(5,5,6),先把两组5个放在天平两侧,若平衡,次品在剩余6个零件中;若不平衡,次品在较轻的5个中。
若次品在剩余6个零件中,将6个零件分成三组(2,2,2),先把两组2个放在天平两侧,若平衡,则次品在剩余2个中,若不平衡,次品在较轻的一组中;再把次品的一组放在天平两次,较轻的一边为次品;
若次品在第一次称的5个零件中,把5个零件分成(2,2,1)三组,把两组2个放在天平两侧,若平衡,剩下的为次品,若不平衡,次品在较轻的一侧;再把较轻的一侧的2个零件放在天平两侧,即可测出次品零件;至少需要3次才能保证找出次品。
【详解】根据分析可知,有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称3次才能保证找到次品。
故答案为:A
4.C
【分析】设小正方形边长为1,求出长方形面积;阴影部分面积为两个三角形面积;根据三角形面积公式:面积=底×高÷2,据此求出阴影部分面积,再用阴影部分面积÷长方形面积,即可解答。
【详解】假设小正方形边长为1。
长方形面积:
1×1×5
=1×5
=5
阴影部分面积:
1×1÷2+1×1÷2
=1÷2+1÷2
=0.5+0.5
=1
1÷5=
长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的。
故答案为:C
5.C
【分析】把一块长方形纸裁成同样大小、面积尽可能大的正方形,且没有剩余,说明正方形的边长是长、宽的最大公因数,把72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数,即是正方形的最大边长。再看长、宽里面分别有几个这样的最大公因数,最后相乘,即可求出至少能裁的张数。
【详解】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即正方形的边长最大是12cm。
72÷12=6(张)
60÷12=5(张)
一共:6×5=30(张)
至少能裁30张。
故答案为:C
6. 9;;25
【分析】小数化分数:一位小数、两位小数、三位小数 化为分数后,分数的分母为10、100、1000 把原来的小数去掉小数点作分子;化成分数后,能约分的要约分;分数的分子相当于被除数,分母相当于除数,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此先将小数化成分数,再根据分数与除法的关系,以及它们通用的基本性质进行填空。
【详解】0.6==;15÷5×3=9;15÷3×5=25
9÷15=0.6==15÷25
7. 10
【分析】判定一个分数的单位看分母,分母是几,分数单位就是几分之一;最小的质数是2,用2减去原分数求出差,再看有几个这样的分数单位即可。
【详解】的分数单位是,最小的质数是2。
,里有10个。
因此的分数单位是,再加上10个这样的分数单位就是最小的质数。
8. 852 250 852,582,528,258
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
从题意可知:在2,5,0,8四个数字中选取3个数字,且数字和是3的倍数的只有2,5,8。即2+5+8=18,将2,5,8三个数字从大到小排列,即可组成的有因数3的最大数。将2,5,8三个数字组成的3的倍数中,个位上是2或8,这个就是2,3的公倍数。
同时是2,5的倍数的个位上的数字一定是0,与较小的2和5组成最小的数即可。
【详解】在2,5,0,8四个数字中任选三个组成的有因数3的最大数是852;同时是2,5的倍数的最小的数是250;2,3的公倍数有852,582,528,258。
9. 4 2
【分析】根据从上面看到的图形可以判断,下层4个小正方体是固定的,第5个小正方体可以在任意一个小正方体上面,所以共4种;根据又从正面看到的图形可以判断,第5个小正方体只能在中间两个小正方体上面,所以共2种。
【详解】
用5个小正方体木块摆,若从上面看到的图形是,有,有4种摆法。如果又从正面看到的图形是,有,有2种摆法。
10. 2 8
【分析】把单位“1”平均分成若干份,取一份的数,叫做分数单位,分数的分子是几,里面就有几个这样的分数单位;在自然数中,除了1和它本身外,没有别的因数的数为质数,据此解题即可。
【详解】2=
10-2=8
所以里面有2个,再加上8个这样的分数单位是最小的质数。
11.;5
【分析】分析题目,把30克糖看作单位“1”,用1除以分成的份数即可得到每份占总数的几分之几;再用30除以分成的份数即可得到每份重多少克。
【详解】1÷6=
30÷6=5(克)
把30克糖平均分成6份,每份占总数的,每份重5克。
12.;0.4
【分析】把这袋糖的总质量看作单位“1”,平均分成5份,用1除以5,求出每份是这袋糖的几分之几;
如果把1千克的糖平均分成10份,用这袋糖的总质量除以10,求出一份是多少千克,再乘4,即是4份是多少千克,结果用小数表示。
【详解】1÷5=
1÷10×4
=0.1×4
=0.4(千克)
一袋糖净重1千克,把这袋糖平均分成5份,每份是这袋糖的();如果把这袋糖平均分成10份,4份用小数表示是(0.4)千克。
13. 2am+2bm abm
【分析】根据题意,一段长方体木料锯去m厘米高,则减少的表面积是4个侧面的面积,即2个长为a厘米、宽为m厘米的长方形的面积与2个长为b厘米、宽为m厘米的长方形的面积之和;根据“长方形的面积=长×宽”求出减少的表面积;
减少的体积是长为a厘米、宽为b厘米、高为m厘米的长方体的体积;根据“长方体的体积=长×宽×高”求出减少的体积。
【详解】a×m×2+b×m×2=(2am+2bm)(平方厘米)
a×b×m=abm(立方厘米)
填空如下:
则它的表面积减少(2am+2bm)平方厘米,体积减少(abm)立方厘米。
14.1500
【分析】根据题意可知,折成长方体后,长方体的长是(30-5×2)cm,宽是(25-5×2)cm,高是5cm;根据长方体容积=长×宽×高,代入数据,即可解答。
【详解】(30-5×2)×(25-5×2)×5
=(30-10)×(25-10)×5
=20×15×5
=300×5
=1500(cm3)
1500cm3=1500mL
这个纸盒的容积是1500。
15.4
【分析】求每小段丝带最长是多少厘米,即求12和20的最大公因数,先把12和20进行分解质因数,这两个数的公有质因数的乘积就是这两个数的最大公因数,据此解答。
【详解】12=2×2×3,20=2×2×5,12和20的最大公因数是2×2=4。
有两条丝带,分别长12cm和20cm,现在要把它们截成同样长的小段(整厘米),不能有剩余,每小段最长是4cm。
16. 186 152
【分析】通过平移,将小正方体上面的面平移到下面,它的表面积=大正方体的表面积+小正方体1个面的面积×4,正方体表面积=棱长×棱长×6;它的体积=大正方体的体积+小正方体的体积,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】5×5×6+3×3×4
=150+36
=186()
5×5×5+3×3×3
=125+27
=152()
它的表面积是186,体积是152。
17.b a
【分析】如果两个数是倍数关系,那么它们的最大公因数是两个数中的较小数,最小公倍数是两个数中的较大数,据此解答。
【详解】如果a÷b=20(a、b均为非0自然数),那么a是b的倍数,a>b,所以a和b的最大公因数是b,最小公倍数是a
18.×
【分析】只有1和它本身两个因数的数是质数;能被2整除的数是偶数;据此举例判断即可。
【详解】2和3都是质数,2+3=5,5是奇数不是偶数;原题说法错误。
故答案为:×
19.×
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数;整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;举例说明。
【详解】例如:3和5是质数
3+5=8,8是偶数
5和7是质数
5+7=12,12是偶数
所以两个质数的和不一定是奇数,原题说法错误。
故答案为:×
20.×
【分析】分数的意义:将一个整体平均分成若干份,其中的一份或几份可以用分数表示。表示将整体平均分成5份,取其中的2份。据此解题。
【详解】淘气和笑笑各有多少压岁钱不明确,那么淘气压岁钱的和笑笑压岁钱的不一定相等,那么他们所捐的钱数是不一定相等的。
故答案为:×
21.√
【分析】可以用字母表示中间数为2a,根据偶数的特征分别表示出3个偶数,比它小的偶数是2a-2,比它大的偶数是2a+2,再相加计算即可。
【详解】2a-2+2a+2a+2=6a
6a是6的倍数,所以原题说法正确。
故答案为:√
22.×
【分析】切下米,分数后面加单位表示具体的长度,用总长度减去切下去的长度即可求出还剩下的长度。
【详解】3-=(米)
还剩下米,原题说法错误。
故答案为:×
23.4.3;3.6;0.72;0.8
;;;2
【详解】略
24.;;70
【分析】(1)按照从左往右的顺序依次计算;
(2)根据加法交换律和结合律把原式写成(-)+(+),再进一步计算即可;
(3)根据乘法结合律先算1.25×8,再和7相乘即可。
【详解】+-
=+-
=-
=
+-+
=(-)+(+)
=+1
=
7×1.25×8
=7×(1.25×8)
=7×10
=70
25.x=;x=;x=65.6
【分析】(1)根据等式的基本性质,方程两边同时减去即可;
(2)根据减数=被减数-差可知x=-,进一步解方程即可;
(3)根据等式的基本性质,方程两边先同时加上97,再同时除以2即可。
【详解】+x=
解:x=-
x=-
x=
-x=
解:x=-
x=-
x=
2x-97=34.2
解:2x=34.2+97
2x=131.2
x=131.2÷2
x=65.6
26.表面积是912dm2,体积是1472dm3
【分析】通过观察可知,这个立体图形的表面积相当于一个长为20dm、宽为8dm、高为6dm的长方体表面积加上一个棱长为8dm的正方体4个面的面积;这个立体图形的体积相当于一个长为20dm、宽为8dm、高为6dm的长方体体积加上一个棱长为8dm的正方体体积;根据长方体的表面积=(长×宽+长×高+宽×高)×2、正方体的表面积=棱长×棱长×6、正方体的体积=棱长×棱长×棱长、长方体的体积=长×宽×高 代入数据即可解答。
【详解】表面积:(20×8+20×6+8×6)×2+8×8×4
=(160+120+48)×2+8×8×4
=328×2+8×8×4
=656+256
=912(dm2)
体积:20×8×6+8×8×8
=960+512
=1472(dm3)
这个立体图形的表面积是912dm2,体积是1472dm3。
27.7月25日
【分析】根据题意,王老师每4天值一次班,李老师每6天值一次班,张老师每8天值一次班,那么他们三人同一天值班的间隔天数就是4、6和8的公倍数;先求出4、6和8的最小公倍数,再加上第一次三人同时值班的日期,即是下一次他们三人同一天值班的日期。
【详解】4=2×2
6=2×3
8=2×2×2
4、6和8的最小公倍数:2×2×2×3=24
即每24天三人同一天值班。
7月1日+24天=7月25日
答:下一次他们三人同一天值班是7月25日。
28.棱长和是100厘米,表面积是408平方厘米,体积是540立方厘米
【分析】根据长方体的底面周长=(长+宽)×2,可知长、宽的和是(30÷2)厘米,即15厘米,因为长和宽的厘米数都是合数,一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数,据此将15拆分为2个合数相加,即6+9;再根据长方体棱长和=(长+宽+高)×4、长方体的表面积=(长×宽+长×高+宽×高)×2、长方体的体积=长×宽×高,代入数据即可求出这个长方体的棱长和、表面积和体积。
【详解】30÷2=15(厘米)
15=6+9
长为9厘米,宽为6厘米,
棱长和:(9+6+10)×4
=25×4
=100(厘米)
表面积:(9×6+9×10+6×10)×2
=(54+90+60)×2
=204×2
=408(平方厘米)
体积:9×6×10=540(立方厘米)
答:这个长方体的棱长和是100厘米,表面积是408平方厘米,体积是540立方厘米。
29.31人
【分析】每行站3人,最后一行少2人,说明这种情况下最后一行只有1人。每行站6人,最后一行少5人,说明这种情况下最后一行也只有1人。又由于每行站5人,结果最后一行只有1人。那么将多的这1人先不考虑,其他的人数就是3、5、6的最小公倍数。5和6互质,这两个数的乘积就是它们的最小公倍数,由于6是3的倍数,所以5和6的最小公倍数也会是3、5、6的最小公倍数。将最小公倍数加1,求出五(3)班最少有多少人。
【详解】5×6+1
=30+1
=31(人)
答:五(3)班最少有31人。
30.72厘米
【分析】根据长方体体积公式:体积=长×宽×高,代入数据,求出左图形里水深24厘米的水的体积,由于体积不变,再用水的体积÷(右图的长×宽),即可求出这时水深,据此解答。
【详解】90×60×24÷(60×30)
=90×60×24÷1800
=5400×24÷1800
=129600÷1800
=72(厘米)
答:这时水深72厘米。
31.
【分析】将全班总人数看作单位“1”。 朗读组的人数占全班人数的,篮球组的人数占全班人数的,两组一共占全班人数的(+),用1减去(+)即可求出参加计算机小组的人数占全班人数的几分之几。
【详解】1-(+)
=1-(+)
=1-
=
答:参加计算机小组的人数占全班人数的。
32.(1);
(2)小时;
(3)杯
【分析】(1)根据统计图可知,小夏休息时间用了(15-5)分钟,总时间是25分钟;用小夏休息时间除以总时间,即可求出小夏回家途中的休息时间占路上总时间的分率;
(2)用小夏完成语文作业的时间-小时,求出小夏完成数学作业的时间,再加上完成语文作业时间,即可求出小夏回家做作业一共用时间;
(3)把这杯牛奶的总量看作单位“1”,先喝了整杯的,即喝了杯;用1-=杯,求出剩下牛奶的量,他发现牛奶凉了,就兑满了热水,又喝了半杯,实际上喝了杯的一半,杯的一半是杯,用先喝的杯再加上杯,即可求出小夏一共喝了多少杯纯牛奶。
【详解】(1)(15-5)÷25
=10÷25
=
答:小夏回家途中的休息时间占路上总时间的。
(2)-+
=-+
=+
=(小时)
答:小夏回家做作业一共用了小时。
(3)1-=(杯)
杯的一半是杯。
+=(杯)
答:小夏一共喝了杯。
答案第14页,共15页
答案第15页,共15页
同课章节目录
