2024-2025年人教版五年级下册数学期末综合训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学期末综合训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 306.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 05:04:26 | ||
图片预览



文档简介
2024-2025年人教版五年级下册数学期末综合训练
一、填空题
1.在0.87、、0.875和0.807中,最小的数是( ),最大的数是( )。
2.一个分数分子和分母的和49,化简后是0.4,这个分数原来是( )。
3.小兵家的电脑密码是一个四位数abcd,a是最小的质数,b是最小的奇数,c是最小的偶数,d是最小的合数。这个密码是( )。
4.小欣经常使用智慧中小学学习平台学习。在智慧中小学平台上的积分达到了1855分,至少增加( )分就是3的倍数,至少增加( )分就同时是2和5的倍数。
5.一个四位数,千位上是最小的奇数,百位上是最小的合数,十位上是最小的质数,个位上是合数又是奇数,这个数写作( )。
6.把一块长8分米、宽6分米、高4分米的长方体木料削成一个最大的正方体,这个正方体的棱长是( )分米,体积是( )立方分米。
7.一个长方体长6cm、宽5cm、高3cm,这个长方体的棱长总和是( )cm,表面积是( )cm2。
8.在括号里填上“>”“<”或“=”。
( ) ( ) ( )
9.若a、b、c是三个互不相等的且大于0的自然数,a+b+c=1155,则它们的最大公因数的最大值为( ),最小公倍数的最小值为( ),最小公倍数的最大值为( )。
10.一个棱长为的正方体水箱中装有半箱水,现在把一块石头完全浸没在水中,水面上升了,这块石块的体积是( )。
11.下面正方体容器的体积是( )cm3,将这个容器装满水,然后把这些水倒入一个从里面量长60cm、宽25cm、高30cm的空的长方体容器里,长方体容器里的水深( )cm。
12.尊敬老人是中华民族的传统美德,爸爸给爷爷买了一箱苹果,这箱苹果有4□个。这个数是50以内最大的质数,这箱苹果有( )个。
二、选择题
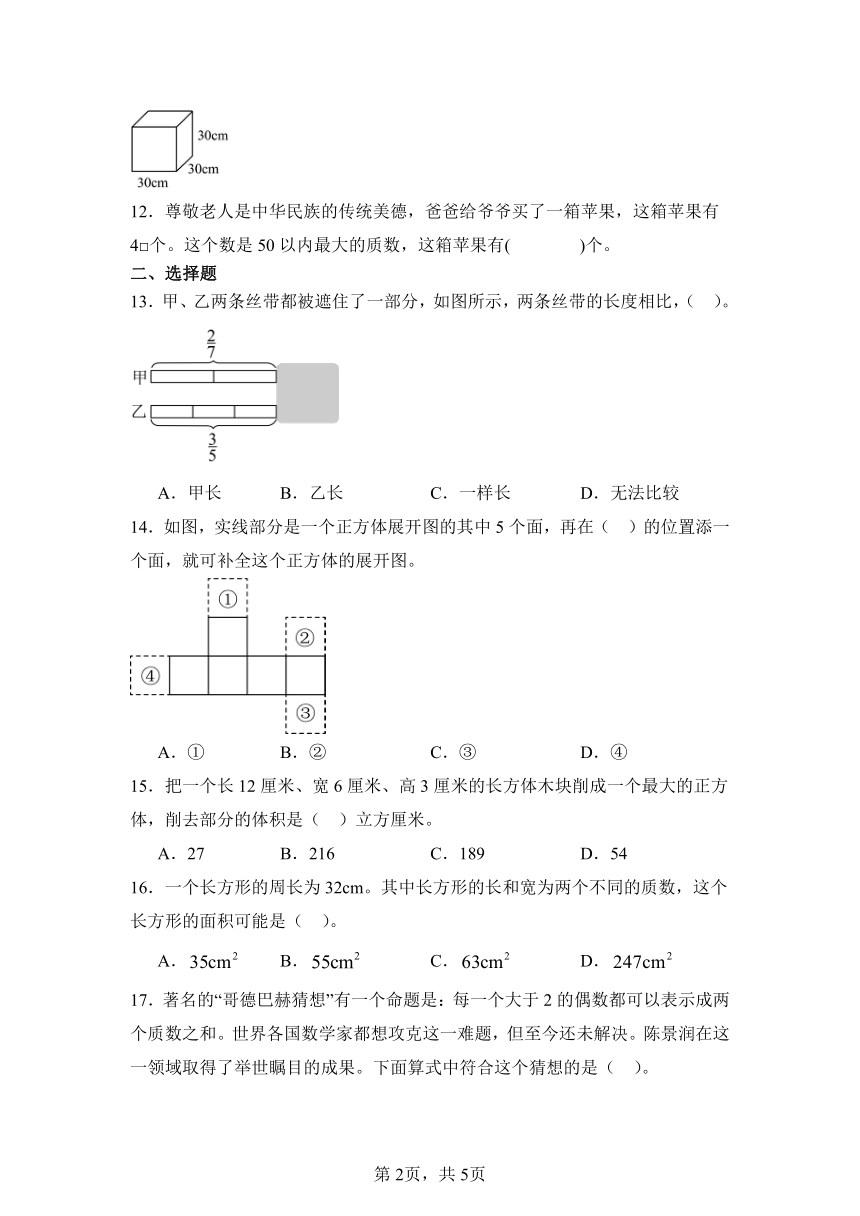
13.甲、乙两条丝带都被遮住了一部分,如图所示,两条丝带的长度相比,( )。
A.甲长 B.乙长 C.一样长 D.无法比较
14.如图,实线部分是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
15.把一个长12厘米、宽6厘米、高3厘米的长方体木块削成一个最大的正方体,削去部分的体积是( )立方厘米。
A.27 B.216 C.189 D.54
16.一个长方形的周长为32cm。其中长方形的长和宽为两个不同的质数,这个长方形的面积可能是( )。
A. B. C. D.
17.著名的“哥德巴赫猜想”有一个命题是:每一个大于2的偶数都可以表示成两个质数之和。世界各国数学家都想攻克这一难题,但至今还未解决。陈景润在这一领域取得了举世瞩目的成果。下面算式中符合这个猜想的是( )。
A.18=1+17 B.5=2+3 C.9=3+3 D.20=7+13
三、判断题
18.时针从2时走到5时,扫过了钟面的。( )
19.正方体的棱长扩大到原来的2倍,表面积扩大到原来的4倍。( )
20.三个连续偶数的和是48,其中最小的偶数是16。( )
21.一个正方体的棱长之和是12cm,它的体积是1cm3。( )
22.爷爷把一块菜地的种了西红柿,种了茄子,种了辣椒。( )
四、计算题
23.直接写得数。
1÷20= 8.65×10= 7.2+12.8= 10÷0.25= 43=
30×0.03= 5÷0.5= 3-0.13= 8.2×0.5= 82=
24.注意观察,用心计算。(能简便运算的要简便运算)
3.75-0.125+6.25- 19.68-3.77-6.23+6.32
25.解方程。
26.求下面几何体的表面积和体积。(单位:cm)
五、解答题
27.用4个长5厘米、宽4厘米、高3厘米的长方体,拼成一个表面积最小的长方体,这个长方体的表面积是多少平方厘米?
28.小明和爸爸骑车去奶奶家,全程18千米。他们先用半小时行了全程的,又用20分钟行了6千米。已经行了多少小时?还剩全程的几分之几?
29.五(1)班共有19幅书法作品参加学校的书法比赛,其中4幅从全校257幅参赛作品中脱颖而出获奖。
(1)五(1)班获奖作品占全班参赛作品的几分之几?
(2)五(1)班参赛作品占全校参赛作品的几分之几?
30.在一块长方形铁皮的两个角上各剪掉一个边长为10厘米的小正方形,并把剪下的两个小正方形焊接到长方形的另一边的中间(如图),然后制成一个无盖的长方体盒子。这个盒子的体积是多少立方分米?(软皮的损耗不计)
31.某城市规定:住宅小区的绿地面积不能少于总占地面积的。某小区,居民楼的占地面积是平方千米,占该小区总占地面积的;道路面积是平方千米,占该小区总占地面积的;其余区域是绿地。该小区的绿地面积符合规定吗?请计算说明理由。
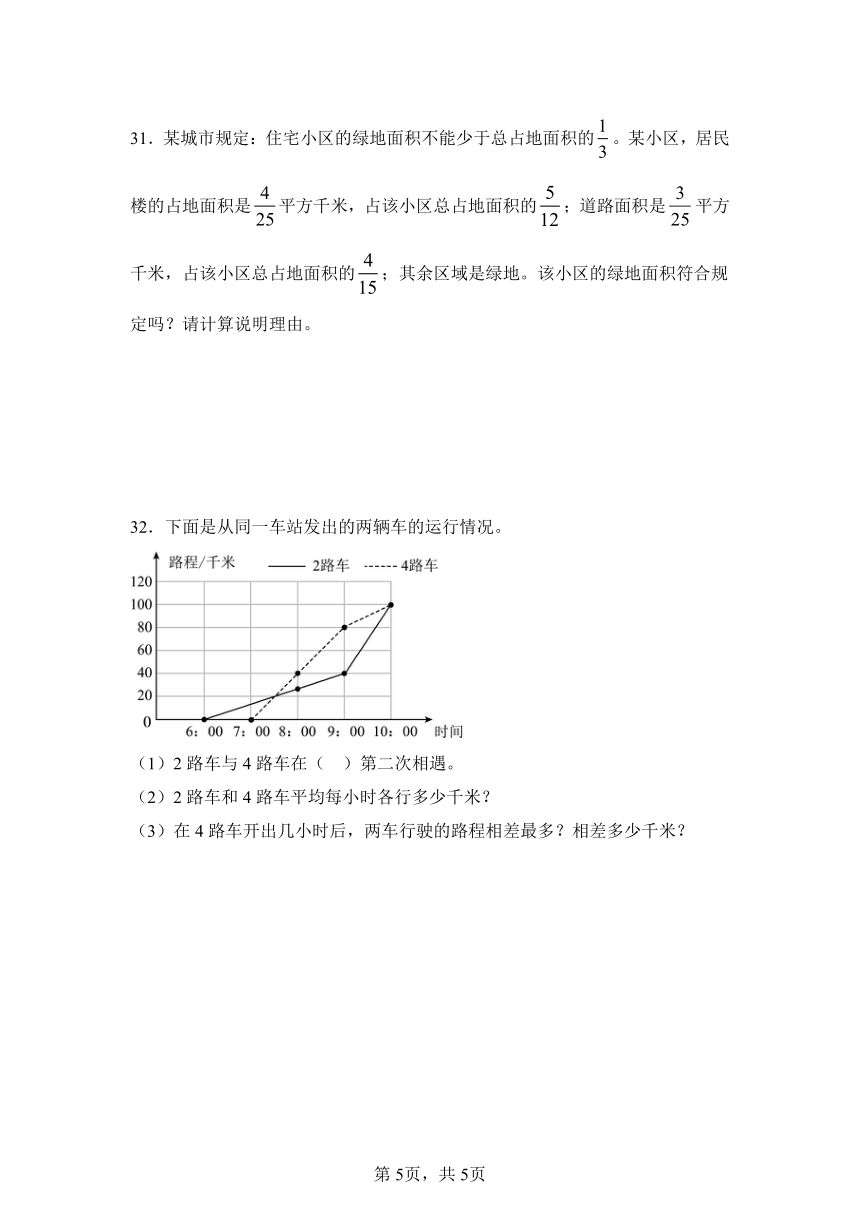
32.下面是从同一车站发出的两辆车的运行情况。
(1)2路车与4路车在( )第二次相遇。
(2)2路车和4路车平均每小时各行多少千米?
(3)在4路车开出几小时后,两车行驶的路程相差最多?相差多少千米?
第2页,共5页
第1页,共5页
《2024-2025年人教版五年级下册数学期末综合训练》参考答案
1. 0.875
【分析】分数化小数:用分数的分子除以分母,据此把分数化成小数,再根据小数比较大小的方法比较大小并找出最大和最小的数即可。
小数比较大小时,先看它们的整数部分,整数部分大的那个数就大;如果整数部分相同,十分位上的数大的那个数就大;如果十分位上的数相同,百分位上的数大的那个数就大……
【详解】=5÷8=0.625
因为0.875>0.87>0.807>0.625,所以0.875>0.87>0.807>。
在0.87、、0.875和0.807中,最小的数是,最大的数是0.875。
2.
【分析】一个分数化简后是0.4,先把0.4化成最简分数;化简后分子与分母的和是2+5=7;
原来分数的分子和分母的和49是化简后分子与分母的和7的7倍,说明原来分数的分子、分母同时除以7,即是最简分数;据此利用倒推法把的分子、分母同时乘7,求出原来的分数。
【详解】0.4==
49÷(5+2)
=49÷7
=7
=
这个分数原来是。
3.2104
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。据此按顺序依次写出abcd这个四位数即可。
【详解】最小的质数是2,最小的奇数是1,最小的偶数是0,最小的合数是4。
所以a是2,b是1,c是0,d是4。
小兵家的电脑密码是一个四位数abcd,a是最小的质数,b是最小的奇数,c是最小的偶数,d是最小的合数。这个密码是2104。
4. 2 5
【分析】一个数各个数位的数字之和是3的倍数,这个数就是3的倍数;根据2的倍数的特征,一个数的个位如果是偶数,这个数就是2的倍数;根据5的倍数的特征,一个数的个位是0或5,这个数就是5的倍数;所以个位上是0的数是2和5的倍数,据此解答即可。
【详解】
21是3的倍数,至少增加2分
至少增加5分这个数的个位上是0
所以,小欣经常使用智慧中小学学习平台学习。在智慧中小学平台上的积分达到了1855分,至少增加2分就是3的倍数,至少增加5分就同时是2和5的倍数。
5.1429
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数。一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数。最小的奇数是1,最小的合数是4,最小的质数是2,一位数中既是合数又是奇数是9。据此解答
【详解】由分析可得:一个四位数,千位上是最小的奇数,百位上是最小的合数,十位上是最小的质数,个位上是合数又是奇数,这个数写作1429。
6. 4 64
【分析】根据题意,把一个长方体木料削成一个最大的正方体,那么正方体的棱长等于长方体最短的棱;根据正方体的体积公式V=a3,代入数据计算,求出这个正方体的体积。
【详解】4<6<8
所以,这个正方体的棱长是4分米。
4×4×4
=16×4
=64(立方分米)
这个正方体的棱长是(4)分米,体积是(64)立方分米。
7. 56 126
【分析】根据长方体的棱长总和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算,求出这个长方体的棱长总和与表面积。
【详解】(6+5+3)×4
=14×4
=56(cm)
(6×5+6×3+5×3)×2
=(30+18+15)×2
=63×2
=126(cm2)
这个长方体的棱长总和是(56)cm,表面积是(126)cm2。
8. = > <
【分析】假分数化整数或带分数:用分子除以分母。当分子是分母的整数倍时,能化成整数,商就是这个整数。当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。据此将前两个空中的假分数化成整数或带分数,再比较。
第三个空,根据真分数<带分数,进行比较。
【详解】=27÷3=9、=;
32÷9=3…5、 、>。
<
9. 165 660 57065085
【分析】首先把1155分解质因数,得到1155=3×5×7×11,再把a、b、c分别写成公因数与某个数的乘积形式,最后根据给定的条件,利用质因数分解和互质性质,进行合理的分析和计算,据此解答。
【详解】由于 a+b+c=1155,而1155=3×5×7×11
令a=mp,b=mq,c=ms,
则1155=mp+mq+ms=m(p+q+s),m为a、b、c的最大公因数,所以p+q+s最小取7,由于a、b、c是三个互不相等,则p、q、s可以是1、2、4。
1155=3×5×7×11=3×5×(1+2+4)×11
则最大公因数m就是3、5、11的乘积。
3×5×11
=15×11
=165
故它们的最大公因数的最大值为165。
为了使最小公倍数尽量小,应使三个数的最大公因数m尽量大,并且使p、q、s的最小公倍数尽量小,所以应使m=165,p=1,q=2、s=4,此时三个数分别为165、330、660,它们的最小公倍数为660。
故最小公倍数的最小值为660。
为了使最小公倍数尽量大,应使三个数两两互质且乘积尽量大。
当三个数的和一定时,为了使它们的乘积尽量大,应使它们尽量接近。相邻的自然数是互质的,1155÷3=385,所以可以令1155=384+385+386,但是在这种情况下384和386有公因数2,而当1155=383+385+387时,三个数两两互质。
它们的最小公倍数为:
383×385×387
=147455×387
=57065085
故最小公倍数的最大值为57065085。
【点睛】本题考查知识点是最大公因数和最小公倍数。公倍数的特殊情况:当两个数成倍数关系时最小公倍数是较大的数;当两个数是互质数时最小公倍数是两个数的乘积。应用分解质因数法分解1155是解题的关键。
10.5.4
【分析】水面上升的体积就是石块的体积,根据长方体体积公式,水箱棱长×棱长×水面上升的高度=石块的体积,据此列式计算。注意统一单位。
【详解】6cm=0.6dm
3×3×0.6=5.4()
这块石块的体积是5.4。
11. 27000 18
【分析】根据正方体体积=棱长×棱长×棱长,即可求出正方体容器的体积;水深相当于长方体的高,根据长方体的高=体积÷底面积,求出水深。
【详解】30×30×30=27000(cm3)
27000÷(60×25)
=27000÷1500
=18(cm)
正方体容器的体积是27000cm3,长方体容器里的水深18cm。
12.47
【分析】一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数, 即除了1和它本身以外不再有其他因数,这样的数叫质数。
【详解】50以内最大的质数是47,这箱苹果有47个。
13.A
【分析】由题意可知,把甲丝带平均分成7份,其中的2份与把乙丝带平均分成5份,取其中的3份,它们是相等的。根据分数的基本性质,把和化为同分母分数,然后比较大小,谁小反而代表整条丝带越长。
【详解】
甲、乙两条丝带都被遮住了一部分,如图所示,两条丝带的长度相比,甲长。
故答案为:A
14.C
【分析】正方体展开图有四大类型,分别是1-4-1型、1-3-2型、2-2-2型、3-3型。据此解题。
【详解】观察目前的正方体展开图,发现再在③的位置添一个面,就可成为正方体展开图的1-4-1型,就可补全这个正方体的展开图。
故答案为:C
15.C
【分析】根据题意,把一个长方体木块削成一个最大的正方体,那么正方体的棱长等于长方体最短的棱;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算,分别求出长方体、正方体的体积,再相减,即可求出削去部分的体积。
【详解】长方体的体积:
12×6×3
=72×3
=216(立方厘米)
正方体的体积:
3×3×3
=9×3
=27(立方厘米)
削去部分的体积:
216-27=189(立方厘米)
所以,削去部分的体积是189立方厘米。
故答案为:C
16.B
【分析】质数:大于1的自然数中,只有1和它本身两个因数的数;长方形的周长=(长+宽)×2,据此先用长方形的周长除以2求出长和宽的和,进而推出长和宽可能的取值;最后根据长方形的面积=长×宽求出面积即可。
【详解】32÷2=16(cm)
16=3+13=5+11
13×3=39(cm2)
11×5=55(cm2)
一个长方形的周长为32cm。其中长方形的长和宽为两个不同的质数,这个长方形的面积可能是39cm2或55cm2。
故答案为:B
17.D
【分析】由题可知:每一个大于2的偶数都能表示成两个质数之和,偶数是能被2整除的整数,质数是指在大于1的自然数中,除了1和它本身以外不再有其它因数的自然数,通过对各选项中数进行判断,来确定是否符合条件。
【详解】A.1不是质数,不满足题干条件,所以该选项错误;
B.5不是大于2的偶数,不符合题干条件,所以该选项错误;
C.9不是大于2的偶数,不满足题干条件,所以该选项错误;
D.20是大于2的偶数,7和13都是质数,20=7 + 13符合“每一个大于2的偶数都可以表示成两个质数之和”,所以该选项正确。
故答案为:D
18.√
【分析】把钟面平均分成12格,根据分数的意义,时针走1格扫过钟面的,时针从2时到5时经过了3格,根据分数与除法的关系,用3除以12,所得结果保留分数形式,再进行约分即可。
【详解】
时针从2时走到5时,扫过了钟面的。原题意法正确。
故答案为:√
19.√
【分析】正方体表面积=棱长×棱长×6,若棱长扩大到原来的2倍,假设原来棱长为1厘米,扩大到原来的2倍为(厘米),分别代入公式计算表面积,再用除法计算,据此解答。
【详解】假设原来棱长为1厘米
1×1=1(厘米)
正方体的棱长扩大到原来的2倍,表面积扩大到原来的4倍。原题说法正确。
故答案为:√
20.×
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。连续偶数的特点,两个相邻的偶数相差2。
用三个连续偶数的和除以3,求出平均数,也是中间的偶数,再用中间的偶数减2,求出这三个连续偶数中最小的偶数。
【详解】48÷3=16
16-2=14
三个连续偶数的和是48,其中最小的偶数是14。
原题说法错误。
故答案为:×
21.√
【分析】正方体的棱长之和=棱长×12,棱长=棱长之和÷12,据此求出棱长,再根据正方体的体积公式:V=a3,把数据代入公式解答。
【详解】12÷12=1(cm)
1×1×1
=1×1
=1(cm3)
它的体积是1 cm3。原题说法正确。
故答案为:√
22.×
【分析】将这块菜地看作单位“1”,种植面积不可能超过单位“1”,将西红柿、茄子和辣椒的对应分率相加,与单位“1”比较即可。
【详解】++
=+
=
>1
故答案为:×
23.0.05;86.5;20;40;64
0.9;10;2.87;4.1;64
【详解】略
24.9;16;10
【分析】(1)先把转化为0.875,根据加法交换律、加法结合律、减法的性质:从一个数中依次减去两个数,等于这个数减去这两个数的和。据此进行简便计算。
(2)(3)根据加法交换律、加法结合律、减法的性质:从一个数中依次减去两个数,等于这个数减去这两个数的和。据此进行简便计算。
【详解】
25.x=2;;
【分析】“”将等式两边同时减去,解出;
“”将等式两边同时减去,解出;
“”将等式两边同时加上,解出。
【详解】
解:
解:
解:
26.(1)308cm2;317cm3;(2)52cm2;23cm3
【分析】(1)通过平移,将正方体上边的面平移到下边,这个组合体的表面积=完整的长方体表面积+正方体4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长。
(2)长方体的顶点位置挖掉一个小正方体,表面积减少了3个正方形的面,里面又出现了同样的3个正方形,组合体的表面积=完整的长方体表面积;组合体的体积=长方体体积-正方体体积。
【详解】(1)(8×6+8×4+6×4)×2+5×5×4
=(48+32+24)×2+100
=104×2+100
=208+100
=308(cm2)
8×6×4+5×5×5
=192+125
=317(cm3)
组合体的表面积是308cm2,体积是317cm3。
(2)(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(cm2)
4×3×2-1×1×1
=24-1
=23(cm3)
组合体的表面积是52cm2,体积是23cm3。
27.236平方厘米
【分析】4个小长方体排列成大长方体,体积不变,要求拼成的长方体表面积最小,应尽量使大长方体的长、宽、高接近。已知每个小长方体长5厘米,宽4厘米,高3厘米,所以将小长方体排成2层,每层5×3的面相接触,长5厘米不变,宽就变成4×2=8厘米,高变成3×2=6厘米。最终拼成的长方体长8厘米,宽5厘米,高6厘米,根据“长方体的表面积=(长×宽+长×高+宽×高)×2”来计算长方体的表面积。
【详解】4×2=8(厘米)
3×2=6(厘米)
(8×5+8×6+5×6)×2
=(40+48+30)×2
=(88+30)×2
=118×2
=236(平方厘米)
答:这个长方体的表面积是236平方厘米。
28.
小时;
【分析】半小时就是小时,根据1小时=60分钟,低级单位转化为高级单位除以进率,把20分钟转化为以时为单位,再已经行了的两个时间相加可得第一问;由题意可知,把全程看作单位“1”,根据求一个数是另一个数的几分之几,用除法计算,用6除以18可得第二次行的是全各程的分率,再用1减两次已走的分率,可得第二问。
【详解】(小时)
(小时)
答:已经行了小时,还剩全程的。
29.(1)
(2)
【分析】A是B的几分之几的计算方法:A÷B=;
(1)五(1)班获奖作品占全班参赛作品的分率=五(1)班获奖作品的数量÷五(1)班参赛作品的数量;
(2)五(1)班参赛作品占全校参赛作品的分率=五(1)班参赛作品的数量÷全校参赛作品的数量;
据此解答即可。
【详解】(1)4÷19=
答:五(1)班获奖作品占全班参赛作品的。
(2)19÷257=
答:五(1)班参赛作品占全校参赛作品的。
30.10立方分米
【分析】看图可知,制成的长方体盒子的长=(60-10)厘米,宽=(40-10×2)厘米,高=10厘米,根据长方体体积=长×宽×高,列式解答即可。根据1立方分米=1000立方厘米,统一单位。
【详解】60-10=50(厘米)
40-10×2
=40-20
=20(厘米)
50×20×10=10000(立方厘米)=10(立方分米)
答:这个盒子的体积是10立方分米。
31.不符合;原因见详解
【分析】把某小区的总面积看作单位“1”,用1减去居民楼占小区面积的分率,减去道路占小区面积的分率,求出绿化面积占小区的分率,再和比较,大于或等于,小区的绿地面积符合规定,否则,就不符合。
【详解】1--
=-
=-
=
=;
>,即>,小区绿化面积不符合规定。
答:小区绿化面积不符合规定。
32.(1)10:00
(2)25千米;33千米
(3)2小时;40千米
【分析】(1)两条线相交于一点,就说明两车相遇了,据此解答;
(2)观察统计图可知:2路车从6:00到10:00,4小时行驶了100千米;4路车从7:00到10:00,3小时行驶了100千米。根据行驶的路程÷行驶的时间=行驶的速度,分别用100除以4、100除以3,即可求出它们各自的速度;
(3)从统计图中可以看出,4路车7:00发车,9:00时两车行驶的路程相差最多,这时4路车开出了(9-7)小时;2路车行驶了40千米,4路车行驶了80千米,把它们相减即可求出差。
【详解】(1)通过分析可得:2路车与4路车在10:00第二次相遇。
(2)2路车:10:00-6:00=4(小时)
100÷4=25(千米/时)
4路车:10:00-7:00=3(小时)
(千米/时)
答:2路车平均每小时行25千米;4路车平均每小时行33千米。
(3)9:00-7:00=2(小时)
80-40=40(千米)
答:在4路车开出2小时后,两车行驶的路程相差最多,相差40千米。
答案第2页,共16页
答案第1页,共16页
一、填空题
1.在0.87、、0.875和0.807中,最小的数是( ),最大的数是( )。
2.一个分数分子和分母的和49,化简后是0.4,这个分数原来是( )。
3.小兵家的电脑密码是一个四位数abcd,a是最小的质数,b是最小的奇数,c是最小的偶数,d是最小的合数。这个密码是( )。
4.小欣经常使用智慧中小学学习平台学习。在智慧中小学平台上的积分达到了1855分,至少增加( )分就是3的倍数,至少增加( )分就同时是2和5的倍数。
5.一个四位数,千位上是最小的奇数,百位上是最小的合数,十位上是最小的质数,个位上是合数又是奇数,这个数写作( )。
6.把一块长8分米、宽6分米、高4分米的长方体木料削成一个最大的正方体,这个正方体的棱长是( )分米,体积是( )立方分米。
7.一个长方体长6cm、宽5cm、高3cm,这个长方体的棱长总和是( )cm,表面积是( )cm2。
8.在括号里填上“>”“<”或“=”。
( ) ( ) ( )
9.若a、b、c是三个互不相等的且大于0的自然数,a+b+c=1155,则它们的最大公因数的最大值为( ),最小公倍数的最小值为( ),最小公倍数的最大值为( )。
10.一个棱长为的正方体水箱中装有半箱水,现在把一块石头完全浸没在水中,水面上升了,这块石块的体积是( )。
11.下面正方体容器的体积是( )cm3,将这个容器装满水,然后把这些水倒入一个从里面量长60cm、宽25cm、高30cm的空的长方体容器里,长方体容器里的水深( )cm。
12.尊敬老人是中华民族的传统美德,爸爸给爷爷买了一箱苹果,这箱苹果有4□个。这个数是50以内最大的质数,这箱苹果有( )个。
二、选择题
13.甲、乙两条丝带都被遮住了一部分,如图所示,两条丝带的长度相比,( )。
A.甲长 B.乙长 C.一样长 D.无法比较
14.如图,实线部分是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
15.把一个长12厘米、宽6厘米、高3厘米的长方体木块削成一个最大的正方体,削去部分的体积是( )立方厘米。
A.27 B.216 C.189 D.54
16.一个长方形的周长为32cm。其中长方形的长和宽为两个不同的质数,这个长方形的面积可能是( )。
A. B. C. D.
17.著名的“哥德巴赫猜想”有一个命题是:每一个大于2的偶数都可以表示成两个质数之和。世界各国数学家都想攻克这一难题,但至今还未解决。陈景润在这一领域取得了举世瞩目的成果。下面算式中符合这个猜想的是( )。
A.18=1+17 B.5=2+3 C.9=3+3 D.20=7+13
三、判断题
18.时针从2时走到5时,扫过了钟面的。( )
19.正方体的棱长扩大到原来的2倍,表面积扩大到原来的4倍。( )
20.三个连续偶数的和是48,其中最小的偶数是16。( )
21.一个正方体的棱长之和是12cm,它的体积是1cm3。( )
22.爷爷把一块菜地的种了西红柿,种了茄子,种了辣椒。( )
四、计算题
23.直接写得数。
1÷20= 8.65×10= 7.2+12.8= 10÷0.25= 43=
30×0.03= 5÷0.5= 3-0.13= 8.2×0.5= 82=
24.注意观察,用心计算。(能简便运算的要简便运算)
3.75-0.125+6.25- 19.68-3.77-6.23+6.32
25.解方程。
26.求下面几何体的表面积和体积。(单位:cm)
五、解答题
27.用4个长5厘米、宽4厘米、高3厘米的长方体,拼成一个表面积最小的长方体,这个长方体的表面积是多少平方厘米?
28.小明和爸爸骑车去奶奶家,全程18千米。他们先用半小时行了全程的,又用20分钟行了6千米。已经行了多少小时?还剩全程的几分之几?
29.五(1)班共有19幅书法作品参加学校的书法比赛,其中4幅从全校257幅参赛作品中脱颖而出获奖。
(1)五(1)班获奖作品占全班参赛作品的几分之几?
(2)五(1)班参赛作品占全校参赛作品的几分之几?
30.在一块长方形铁皮的两个角上各剪掉一个边长为10厘米的小正方形,并把剪下的两个小正方形焊接到长方形的另一边的中间(如图),然后制成一个无盖的长方体盒子。这个盒子的体积是多少立方分米?(软皮的损耗不计)
31.某城市规定:住宅小区的绿地面积不能少于总占地面积的。某小区,居民楼的占地面积是平方千米,占该小区总占地面积的;道路面积是平方千米,占该小区总占地面积的;其余区域是绿地。该小区的绿地面积符合规定吗?请计算说明理由。
32.下面是从同一车站发出的两辆车的运行情况。
(1)2路车与4路车在( )第二次相遇。
(2)2路车和4路车平均每小时各行多少千米?
(3)在4路车开出几小时后,两车行驶的路程相差最多?相差多少千米?
第2页,共5页
第1页,共5页
《2024-2025年人教版五年级下册数学期末综合训练》参考答案
1. 0.875
【分析】分数化小数:用分数的分子除以分母,据此把分数化成小数,再根据小数比较大小的方法比较大小并找出最大和最小的数即可。
小数比较大小时,先看它们的整数部分,整数部分大的那个数就大;如果整数部分相同,十分位上的数大的那个数就大;如果十分位上的数相同,百分位上的数大的那个数就大……
【详解】=5÷8=0.625
因为0.875>0.87>0.807>0.625,所以0.875>0.87>0.807>。
在0.87、、0.875和0.807中,最小的数是,最大的数是0.875。
2.
【分析】一个分数化简后是0.4,先把0.4化成最简分数;化简后分子与分母的和是2+5=7;
原来分数的分子和分母的和49是化简后分子与分母的和7的7倍,说明原来分数的分子、分母同时除以7,即是最简分数;据此利用倒推法把的分子、分母同时乘7,求出原来的分数。
【详解】0.4==
49÷(5+2)
=49÷7
=7
=
这个分数原来是。
3.2104
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。据此按顺序依次写出abcd这个四位数即可。
【详解】最小的质数是2,最小的奇数是1,最小的偶数是0,最小的合数是4。
所以a是2,b是1,c是0,d是4。
小兵家的电脑密码是一个四位数abcd,a是最小的质数,b是最小的奇数,c是最小的偶数,d是最小的合数。这个密码是2104。
4. 2 5
【分析】一个数各个数位的数字之和是3的倍数,这个数就是3的倍数;根据2的倍数的特征,一个数的个位如果是偶数,这个数就是2的倍数;根据5的倍数的特征,一个数的个位是0或5,这个数就是5的倍数;所以个位上是0的数是2和5的倍数,据此解答即可。
【详解】
21是3的倍数,至少增加2分
至少增加5分这个数的个位上是0
所以,小欣经常使用智慧中小学学习平台学习。在智慧中小学平台上的积分达到了1855分,至少增加2分就是3的倍数,至少增加5分就同时是2和5的倍数。
5.1429
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数。一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数。最小的奇数是1,最小的合数是4,最小的质数是2,一位数中既是合数又是奇数是9。据此解答
【详解】由分析可得:一个四位数,千位上是最小的奇数,百位上是最小的合数,十位上是最小的质数,个位上是合数又是奇数,这个数写作1429。
6. 4 64
【分析】根据题意,把一个长方体木料削成一个最大的正方体,那么正方体的棱长等于长方体最短的棱;根据正方体的体积公式V=a3,代入数据计算,求出这个正方体的体积。
【详解】4<6<8
所以,这个正方体的棱长是4分米。
4×4×4
=16×4
=64(立方分米)
这个正方体的棱长是(4)分米,体积是(64)立方分米。
7. 56 126
【分析】根据长方体的棱长总和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算,求出这个长方体的棱长总和与表面积。
【详解】(6+5+3)×4
=14×4
=56(cm)
(6×5+6×3+5×3)×2
=(30+18+15)×2
=63×2
=126(cm2)
这个长方体的棱长总和是(56)cm,表面积是(126)cm2。
8. = > <
【分析】假分数化整数或带分数:用分子除以分母。当分子是分母的整数倍时,能化成整数,商就是这个整数。当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。据此将前两个空中的假分数化成整数或带分数,再比较。
第三个空,根据真分数<带分数,进行比较。
【详解】=27÷3=9、=;
32÷9=3…5、 、>。
<
9. 165 660 57065085
【分析】首先把1155分解质因数,得到1155=3×5×7×11,再把a、b、c分别写成公因数与某个数的乘积形式,最后根据给定的条件,利用质因数分解和互质性质,进行合理的分析和计算,据此解答。
【详解】由于 a+b+c=1155,而1155=3×5×7×11
令a=mp,b=mq,c=ms,
则1155=mp+mq+ms=m(p+q+s),m为a、b、c的最大公因数,所以p+q+s最小取7,由于a、b、c是三个互不相等,则p、q、s可以是1、2、4。
1155=3×5×7×11=3×5×(1+2+4)×11
则最大公因数m就是3、5、11的乘积。
3×5×11
=15×11
=165
故它们的最大公因数的最大值为165。
为了使最小公倍数尽量小,应使三个数的最大公因数m尽量大,并且使p、q、s的最小公倍数尽量小,所以应使m=165,p=1,q=2、s=4,此时三个数分别为165、330、660,它们的最小公倍数为660。
故最小公倍数的最小值为660。
为了使最小公倍数尽量大,应使三个数两两互质且乘积尽量大。
当三个数的和一定时,为了使它们的乘积尽量大,应使它们尽量接近。相邻的自然数是互质的,1155÷3=385,所以可以令1155=384+385+386,但是在这种情况下384和386有公因数2,而当1155=383+385+387时,三个数两两互质。
它们的最小公倍数为:
383×385×387
=147455×387
=57065085
故最小公倍数的最大值为57065085。
【点睛】本题考查知识点是最大公因数和最小公倍数。公倍数的特殊情况:当两个数成倍数关系时最小公倍数是较大的数;当两个数是互质数时最小公倍数是两个数的乘积。应用分解质因数法分解1155是解题的关键。
10.5.4
【分析】水面上升的体积就是石块的体积,根据长方体体积公式,水箱棱长×棱长×水面上升的高度=石块的体积,据此列式计算。注意统一单位。
【详解】6cm=0.6dm
3×3×0.6=5.4()
这块石块的体积是5.4。
11. 27000 18
【分析】根据正方体体积=棱长×棱长×棱长,即可求出正方体容器的体积;水深相当于长方体的高,根据长方体的高=体积÷底面积,求出水深。
【详解】30×30×30=27000(cm3)
27000÷(60×25)
=27000÷1500
=18(cm)
正方体容器的体积是27000cm3,长方体容器里的水深18cm。
12.47
【分析】一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数, 即除了1和它本身以外不再有其他因数,这样的数叫质数。
【详解】50以内最大的质数是47,这箱苹果有47个。
13.A
【分析】由题意可知,把甲丝带平均分成7份,其中的2份与把乙丝带平均分成5份,取其中的3份,它们是相等的。根据分数的基本性质,把和化为同分母分数,然后比较大小,谁小反而代表整条丝带越长。
【详解】
甲、乙两条丝带都被遮住了一部分,如图所示,两条丝带的长度相比,甲长。
故答案为:A
14.C
【分析】正方体展开图有四大类型,分别是1-4-1型、1-3-2型、2-2-2型、3-3型。据此解题。
【详解】观察目前的正方体展开图,发现再在③的位置添一个面,就可成为正方体展开图的1-4-1型,就可补全这个正方体的展开图。
故答案为:C
15.C
【分析】根据题意,把一个长方体木块削成一个最大的正方体,那么正方体的棱长等于长方体最短的棱;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算,分别求出长方体、正方体的体积,再相减,即可求出削去部分的体积。
【详解】长方体的体积:
12×6×3
=72×3
=216(立方厘米)
正方体的体积:
3×3×3
=9×3
=27(立方厘米)
削去部分的体积:
216-27=189(立方厘米)
所以,削去部分的体积是189立方厘米。
故答案为:C
16.B
【分析】质数:大于1的自然数中,只有1和它本身两个因数的数;长方形的周长=(长+宽)×2,据此先用长方形的周长除以2求出长和宽的和,进而推出长和宽可能的取值;最后根据长方形的面积=长×宽求出面积即可。
【详解】32÷2=16(cm)
16=3+13=5+11
13×3=39(cm2)
11×5=55(cm2)
一个长方形的周长为32cm。其中长方形的长和宽为两个不同的质数,这个长方形的面积可能是39cm2或55cm2。
故答案为:B
17.D
【分析】由题可知:每一个大于2的偶数都能表示成两个质数之和,偶数是能被2整除的整数,质数是指在大于1的自然数中,除了1和它本身以外不再有其它因数的自然数,通过对各选项中数进行判断,来确定是否符合条件。
【详解】A.1不是质数,不满足题干条件,所以该选项错误;
B.5不是大于2的偶数,不符合题干条件,所以该选项错误;
C.9不是大于2的偶数,不满足题干条件,所以该选项错误;
D.20是大于2的偶数,7和13都是质数,20=7 + 13符合“每一个大于2的偶数都可以表示成两个质数之和”,所以该选项正确。
故答案为:D
18.√
【分析】把钟面平均分成12格,根据分数的意义,时针走1格扫过钟面的,时针从2时到5时经过了3格,根据分数与除法的关系,用3除以12,所得结果保留分数形式,再进行约分即可。
【详解】
时针从2时走到5时,扫过了钟面的。原题意法正确。
故答案为:√
19.√
【分析】正方体表面积=棱长×棱长×6,若棱长扩大到原来的2倍,假设原来棱长为1厘米,扩大到原来的2倍为(厘米),分别代入公式计算表面积,再用除法计算,据此解答。
【详解】假设原来棱长为1厘米
1×1=1(厘米)
正方体的棱长扩大到原来的2倍,表面积扩大到原来的4倍。原题说法正确。
故答案为:√
20.×
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。连续偶数的特点,两个相邻的偶数相差2。
用三个连续偶数的和除以3,求出平均数,也是中间的偶数,再用中间的偶数减2,求出这三个连续偶数中最小的偶数。
【详解】48÷3=16
16-2=14
三个连续偶数的和是48,其中最小的偶数是14。
原题说法错误。
故答案为:×
21.√
【分析】正方体的棱长之和=棱长×12,棱长=棱长之和÷12,据此求出棱长,再根据正方体的体积公式:V=a3,把数据代入公式解答。
【详解】12÷12=1(cm)
1×1×1
=1×1
=1(cm3)
它的体积是1 cm3。原题说法正确。
故答案为:√
22.×
【分析】将这块菜地看作单位“1”,种植面积不可能超过单位“1”,将西红柿、茄子和辣椒的对应分率相加,与单位“1”比较即可。
【详解】++
=+
=
>1
故答案为:×
23.0.05;86.5;20;40;64
0.9;10;2.87;4.1;64
【详解】略
24.9;16;10
【分析】(1)先把转化为0.875,根据加法交换律、加法结合律、减法的性质:从一个数中依次减去两个数,等于这个数减去这两个数的和。据此进行简便计算。
(2)(3)根据加法交换律、加法结合律、减法的性质:从一个数中依次减去两个数,等于这个数减去这两个数的和。据此进行简便计算。
【详解】
25.x=2;;
【分析】“”将等式两边同时减去,解出;
“”将等式两边同时减去,解出;
“”将等式两边同时加上,解出。
【详解】
解:
解:
解:
26.(1)308cm2;317cm3;(2)52cm2;23cm3
【分析】(1)通过平移,将正方体上边的面平移到下边,这个组合体的表面积=完整的长方体表面积+正方体4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长。
(2)长方体的顶点位置挖掉一个小正方体,表面积减少了3个正方形的面,里面又出现了同样的3个正方形,组合体的表面积=完整的长方体表面积;组合体的体积=长方体体积-正方体体积。
【详解】(1)(8×6+8×4+6×4)×2+5×5×4
=(48+32+24)×2+100
=104×2+100
=208+100
=308(cm2)
8×6×4+5×5×5
=192+125
=317(cm3)
组合体的表面积是308cm2,体积是317cm3。
(2)(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(cm2)
4×3×2-1×1×1
=24-1
=23(cm3)
组合体的表面积是52cm2,体积是23cm3。
27.236平方厘米
【分析】4个小长方体排列成大长方体,体积不变,要求拼成的长方体表面积最小,应尽量使大长方体的长、宽、高接近。已知每个小长方体长5厘米,宽4厘米,高3厘米,所以将小长方体排成2层,每层5×3的面相接触,长5厘米不变,宽就变成4×2=8厘米,高变成3×2=6厘米。最终拼成的长方体长8厘米,宽5厘米,高6厘米,根据“长方体的表面积=(长×宽+长×高+宽×高)×2”来计算长方体的表面积。
【详解】4×2=8(厘米)
3×2=6(厘米)
(8×5+8×6+5×6)×2
=(40+48+30)×2
=(88+30)×2
=118×2
=236(平方厘米)
答:这个长方体的表面积是236平方厘米。
28.
小时;
【分析】半小时就是小时,根据1小时=60分钟,低级单位转化为高级单位除以进率,把20分钟转化为以时为单位,再已经行了的两个时间相加可得第一问;由题意可知,把全程看作单位“1”,根据求一个数是另一个数的几分之几,用除法计算,用6除以18可得第二次行的是全各程的分率,再用1减两次已走的分率,可得第二问。
【详解】(小时)
(小时)
答:已经行了小时,还剩全程的。
29.(1)
(2)
【分析】A是B的几分之几的计算方法:A÷B=;
(1)五(1)班获奖作品占全班参赛作品的分率=五(1)班获奖作品的数量÷五(1)班参赛作品的数量;
(2)五(1)班参赛作品占全校参赛作品的分率=五(1)班参赛作品的数量÷全校参赛作品的数量;
据此解答即可。
【详解】(1)4÷19=
答:五(1)班获奖作品占全班参赛作品的。
(2)19÷257=
答:五(1)班参赛作品占全校参赛作品的。
30.10立方分米
【分析】看图可知,制成的长方体盒子的长=(60-10)厘米,宽=(40-10×2)厘米,高=10厘米,根据长方体体积=长×宽×高,列式解答即可。根据1立方分米=1000立方厘米,统一单位。
【详解】60-10=50(厘米)
40-10×2
=40-20
=20(厘米)
50×20×10=10000(立方厘米)=10(立方分米)
答:这个盒子的体积是10立方分米。
31.不符合;原因见详解
【分析】把某小区的总面积看作单位“1”,用1减去居民楼占小区面积的分率,减去道路占小区面积的分率,求出绿化面积占小区的分率,再和比较,大于或等于,小区的绿地面积符合规定,否则,就不符合。
【详解】1--
=-
=-
=
=;
>,即>,小区绿化面积不符合规定。
答:小区绿化面积不符合规定。
32.(1)10:00
(2)25千米;33千米
(3)2小时;40千米
【分析】(1)两条线相交于一点,就说明两车相遇了,据此解答;
(2)观察统计图可知:2路车从6:00到10:00,4小时行驶了100千米;4路车从7:00到10:00,3小时行驶了100千米。根据行驶的路程÷行驶的时间=行驶的速度,分别用100除以4、100除以3,即可求出它们各自的速度;
(3)从统计图中可以看出,4路车7:00发车,9:00时两车行驶的路程相差最多,这时4路车开出了(9-7)小时;2路车行驶了40千米,4路车行驶了80千米,把它们相减即可求出差。
【详解】(1)通过分析可得:2路车与4路车在10:00第二次相遇。
(2)2路车:10:00-6:00=4(小时)
100÷4=25(千米/时)
4路车:10:00-7:00=3(小时)
(千米/时)
答:2路车平均每小时行25千米;4路车平均每小时行33千米。
(3)9:00-7:00=2(小时)
80-40=40(千米)
答:在4路车开出2小时后,两车行驶的路程相差最多,相差40千米。
答案第2页,共16页
答案第1页,共16页
同课章节目录
