湘教版2024—2025学年七年级下学期数学第三次月考考试模拟试卷(含答案)
文档属性
| 名称 | 湘教版2024—2025学年七年级下学期数学第三次月考考试模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 511.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版2024—2025学年七年级下学期数学第三次月考考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.《国语 楚语》记载:“夫美也者,上下、内外、大小、远近皆无害焉,故曰美.”这一记载充分表明传统美的本质特征在于对称和谐.下列四个图案中,是轴对称图形的是( )
A. B. C. D.
2.下列各数中,是无理数的是( )
A.3.1415926 B. C. D.2
3.南昌市春季某日的最高气温是22℃,最低气温是12℃,则南昌当日气温t(℃)的变化范围是( )
A.t≤22 B.t≥12 C.12<t<22 D.12≤t≤22
4.有一个数值转换器,流程如图:当输入的x值为64时,输出的y值是( )
A.2 B. C.±2 D.
5.利用计算器计算出的下表中各数的算术平方根如下:
… …
… 0.25 0.7906 2.5 7.906 25 79.06 250 …
根据以上规律,若≈1.30,≈4.11,则≈( )
A.13.0 B.130 C.41.1 D.411
6.若关于x的不等式5x+m≥7x的正整数解是1、2、3、4.则m的取值范围为( )
A.m<10 B.m≥8 C.8≤m≤10 D.8≤m<10
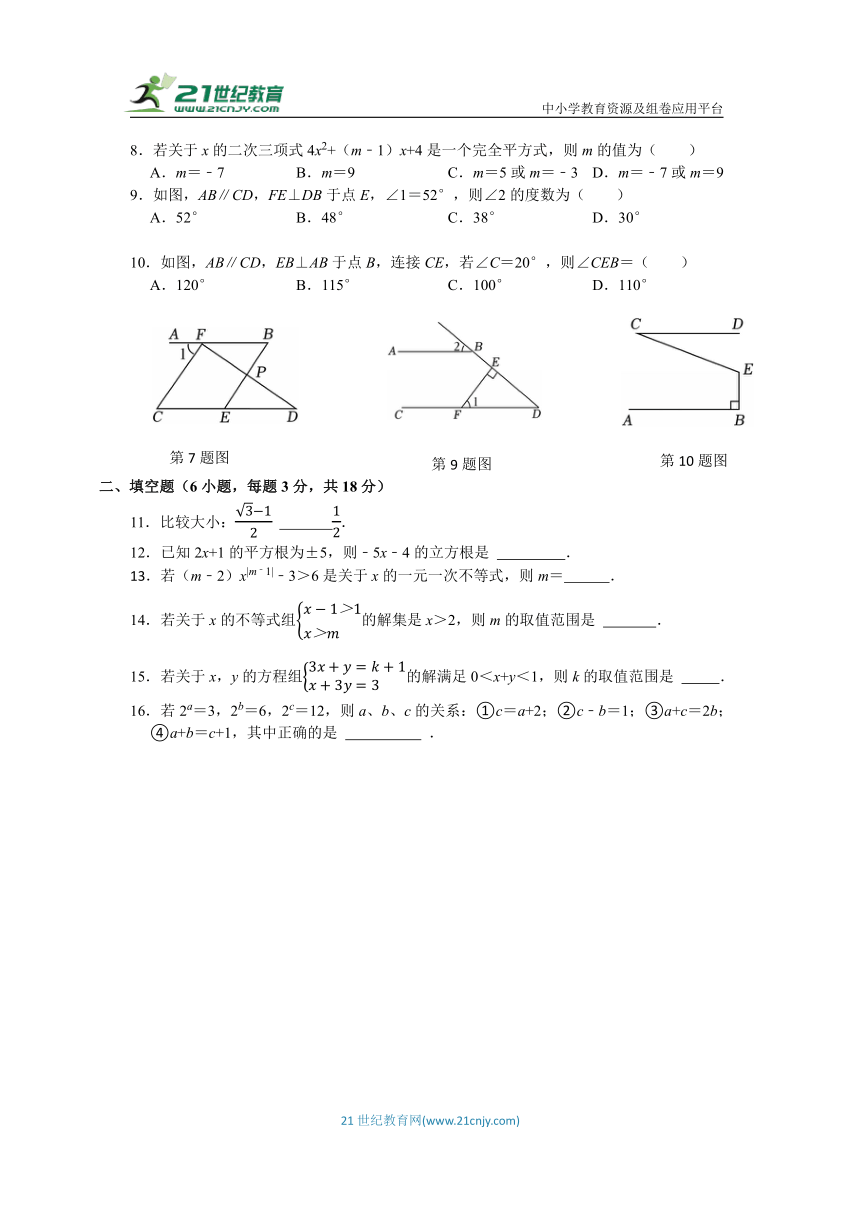
7.如图,下列条件不能判定CF∥BE的是( )
A.∠1=∠B B.∠1=∠C
C.∠CFB+∠B=180° D.∠CFP=∠FPB
8.若关于x的二次三项式4x2+(m﹣1)x+4是一个完全平方式,则m的值为( )
A.m=﹣7 B.m=9 C.m=5或m=﹣3 D.m=﹣7或m=9
9.如图,AB∥CD,FE⊥DB于点E,∠1=52°,则∠2的度数为( )
A.52° B.48° C.38° D.30°
10.如图,AB∥CD,EB⊥AB于点B,连接CE,若∠C=20°,则∠CEB=( )
A.120° B.115° C.100° D.110°
二、填空题(6小题,每题3分,共18分)
11.比较大小: .
12.已知2x+1的平方根为±5,则﹣5x﹣4的立方根是 .
13.若(m﹣2)x|m﹣1|﹣3>6是关于x的一元一次不等式,则m= .
14.若关于x的不等式组的解集是x>2,则m的取值范围是 .
15.若关于x,y的方程组的解满足0<x+y<1,则k的取值范围是 .
16.若2a=3,2b=6,2c=12,则a、b、c的关系:①c=a+2;②c﹣b=1;③a+c=2b;④a+b=c+1,其中正确的是 .
第II卷
湘教版2024—2025学年七年级下学期数学第三次月考考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
18.如果一个正数a的两个平方根是2x﹣2和6﹣3x.
求(1)x和这个正数a的值;
(2)17+3a的立方根.
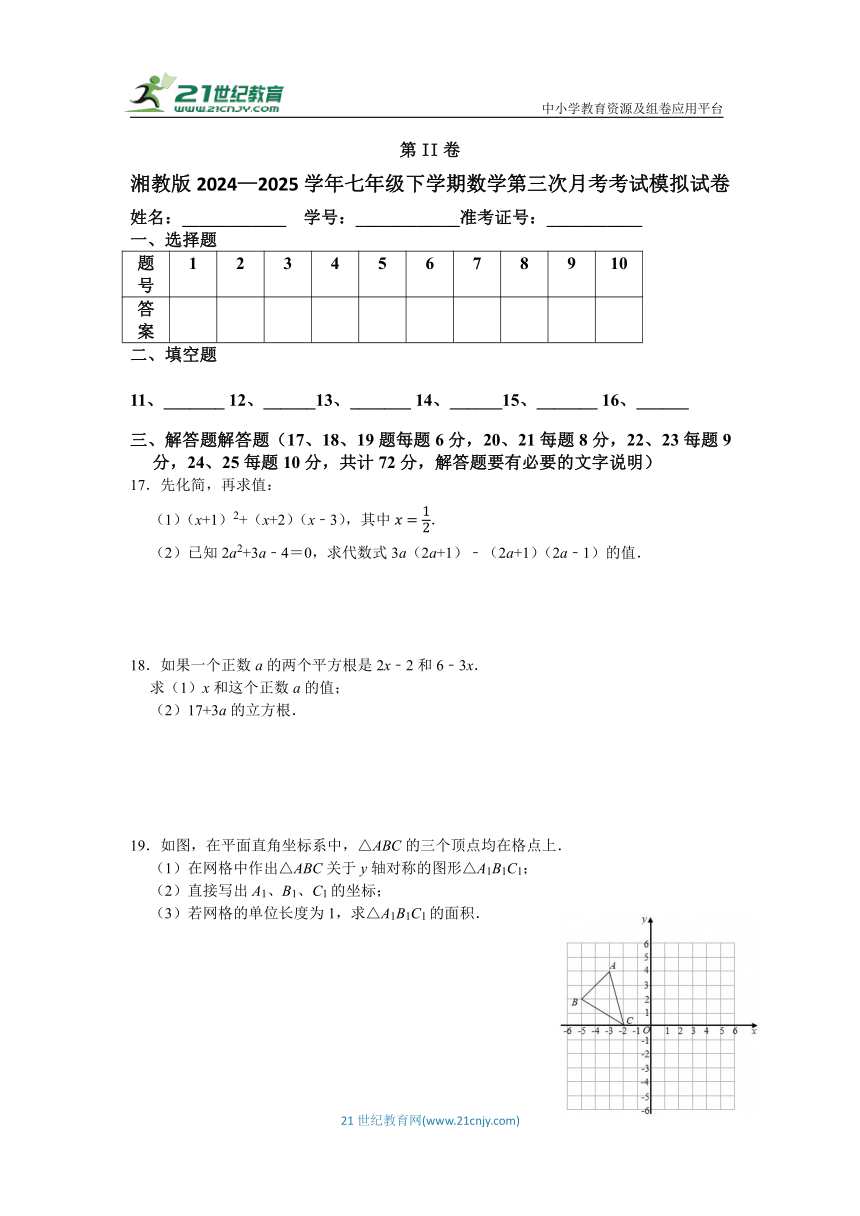
19.如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)在网格中作出△ABC关于y轴对称的图形△A1B1C1;
(2)直接写出A1、B1、C1的坐标;
(3)若网格的单位长度为1,求△A1B1C1的面积.
20.如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN点PA、PB分别相交于点E、F,已知MN=8cm.
(1)求△OEF的周长;
(2)连接PM、PN,若∠APB=α,求∠MPN.(用含a的代数式表示)
21.有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t,5辆大货车与6辆小货车一次可以运货35t.
(1)3辆大货车与5辆小货车一次可以运货多少吨?
(2)计划用两种货车共12辆运输一批货物,大货车每次需运费3000元,小货车每次需运费1800元,若运输的总货物不少于38t,且总费用不超过32000元,请列出所有运输方案,并计算说明哪种方案所需费用最少,最少费用是多少?
22.已知方程组的解满足x为非正数,y为负数.
(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解集为x>1.
23.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
24.我们约定:若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“美美与共方程”,例如:方程x﹣2=2的解为x=4,而不等式组的解集为3<x<5,不难发现x=4在3<x<5的范围内,所以方程x﹣2=2是不等式组的“美美与共方程”.
(1)在一元一次方程①6x﹣7=4x﹣5;②2x+5=3(x﹣1);③中,不等式组的“美美与共方程”是 ;(填序号)
(2)若关于x的方程是不等式组的“美美与共方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“美美与共方程”,且此时该不等式组有7个整数解,若M=2m+3n﹣p,3m﹣n+p=4,m+n+p=6,求M的取值范围.
25.已知直线AB∥CD,直线EF与AB,CD分别交于点E,F,∠EFC=α(0°<α<90°).将一个直角三角板OPQ按如图1所示放置,使点Q,O分别在直线AB,CD上,∠P=90°,∠POQ=60°,∠PQO=30°,OP∥EF.
(1)若α=80°,分别求∠QOF与∠AQP的度数;
(2)求∠POC+∠AQP的度数;
(3)将直角三角板OPQ沿AB向右平移.
①如图2,当点Q与点E重合时,若EO恰好平分∠AEF,求α的值;
②作∠FOQ的平分线OG,交直线AB于点G,在整个平移过程中,直接写出∠AGO的度数(用含α 的式子表示).
参考答案
一、选择题
1—10:BCDBC BDDCD
二、填空题
11.【解答】解:∵
1,
∵1<3<4,
∴12,
∴1,
∴1<0,
∴.
故答案为:<.
12.【解答】解:由题意得:2x+1=25,
解得:x=12,
﹣5x﹣4=﹣5×12﹣4=﹣64,
﹣64的立方根是﹣4,
故答案为:﹣4.
13.【解答】解:根据题意,得
|m﹣1|=1且m﹣2≠0,
解得,m=0.
故答案为:0.
14.【解答】解:解x﹣1>1,得:x>2,
∵不等式组的解集是x>2,
∴m≤2,
故答案为:m≤2.
15.【解答】解:两方程相加得4x+4y=k+4,
∵0<x+y<1,
∴0<4x+4y<4,
则0<k+4<4,
解得﹣4<k<0,
故答案为:﹣4<k<0.
16.【解答】解:①②③.
三、解答题
17.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
18.【解答】解:(1)∵一个正数a的两个平方根是2x﹣2和6﹣3x,
∴2x﹣2+6﹣3x=0,
∴x=4.
∴2x﹣2=2×4﹣2=6,
∴a=36.
(2)∵a=36,
∴17+3a=17+3×36=125,
∵125的立方根为5,
∴17+3a的立方根为5.
19.【解答】解:(1)如图,△A1B1C1即为所求.
(2)A1(3,4),B1(5,2),C1(2,0);
(3)△A1B1C1的面积=3×41×42×22×3=5,
20.解:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF
=ME+EF+FN=MN
=8(cm);
(2)如图,连接PM,PN,PO,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2a.
21.解:(1)∵l1是AB边的垂直平分线,
14.【解答】解:(1)设1辆大货车一次运货xt,1辆小货车一次运货yt,
由题意得:,
解得:,
∴3x+5y=12+12.5=24.5t,
答:3辆大货车与5辆小货车一次可以运货24.5t;
(2)设用大货车a辆,则小货车(12﹣a)辆,总运费为z元,
由题意得:,
解得:5≤a≤8,
∴a的整数解有:6,7,8三个,
∴有3种运输方案,分别为:
方案一:大货车6辆,小货车6辆,
方案二:大货车7辆,小货车5辆,
方案三:大货车8辆,小货车4辆;
由题意得:z=3000a+1800(12﹣a)=1200a+21600,
当选方案一时:z=1200×6+21600=28800(元),
当选方案二时:z=1200×7+21600=30000(元),
当选方案三时:z=1200×8+21600=31200(元),
∵28800<30000<31200,
即选方案一费用最少,为28800元.
22.【解答】解:(1)解原方程组得:,
∵x≤0,y<0,
∴,
解得﹣2<m≤3;
(2)|m﹣3|﹣|m+2|=3﹣m﹣m﹣2=1﹣2m;
(3)解不等式2mx+x<2m+1得(2m+1)x<2m+1,
∵x>1,∴2m+1<0,
∴m,
∴﹣2<m,
∴m=﹣1.
23.【解答】解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
24.【解答】解:(1)①6x﹣7=4x﹣5,
解得x=1,
②2x+5=3(x﹣1),
解得x=8,
③,
解得x,
解不等式组,得x≤4,
由题:①③是不等式组的“美美与共方程”.
故答案为:①③;
(2)解关于x的方程,得x=2k+1,
解不等式组,得x,
由题意得:2k+1,
解得:k.
故k的取值范围是k;
(3)解方程,得x=2m﹣1,
解不等式组,得,
由题意得: ①,
且 ②,
解不等式①得:,
解不等式②得:3≤m<5,
∴3≤m≤4;
,
解得,
∴,
解得:19≤M≤26.
故M的取值范围是19≤M≤26
25.【解答】解:(1)如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∴∠OPQ=∠OPM+∠QOM=90°,
∵OP∥EF,
∴∠EFC=∠POC=α=80°,
∴∠AQP=90°﹣80°=10°,
∵AB∥CD,
∴∠QOF=∠AQO=∠AQP+∠PQO=10°+30°=40°,
即∠QOF=40°,∠AQP=10°;
(2)∠POC+∠AQP=90°,
如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∵∠OPQ=∠OPM+∠QOM=90°,
∴∠POC+∠AQP=90°;
(3)①如图2,∵EO恰好平分∠AEF,
∴∠AEO=∠OEF,
∵AB∥CD,
∴∠AEO=∠EOF=∠OEF,
∵OP∥EF,
∴∠POC=∠EFC=α,
∴∠EOF=180°﹣60°﹣α,
在△EOF中,由内角和定理可得,
∠EOF+∠OEF+∠OFE=180°,
即2×(180°﹣60°﹣α)+α=180°,
解得α=60°;
②如图1,∠AGO=∠GOF∠FOQ,
∵∠FOQ=180°﹣60°﹣α=120°﹣α,
∴∠AGO(120°﹣α)=60°α;
如图3,∵PO∥EF,
∴∠POF=∠EFC=α,
∴∠QOF=60°+α,
∵OG平分∠QOF,
∴∠GOF∠QOF=30°α,
∵AB∥CD,
∴∠AGO=180°﹣∠GOF=150°α,
综上所述∠AGO=150°α或∠AGO=60°α.
21世纪教育网(www.21cnjy.com)
湘教版2024—2025学年七年级下学期数学第三次月考考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.《国语 楚语》记载:“夫美也者,上下、内外、大小、远近皆无害焉,故曰美.”这一记载充分表明传统美的本质特征在于对称和谐.下列四个图案中,是轴对称图形的是( )
A. B. C. D.
2.下列各数中,是无理数的是( )
A.3.1415926 B. C. D.2
3.南昌市春季某日的最高气温是22℃,最低气温是12℃,则南昌当日气温t(℃)的变化范围是( )
A.t≤22 B.t≥12 C.12<t<22 D.12≤t≤22
4.有一个数值转换器,流程如图:当输入的x值为64时,输出的y值是( )
A.2 B. C.±2 D.
5.利用计算器计算出的下表中各数的算术平方根如下:
… …
… 0.25 0.7906 2.5 7.906 25 79.06 250 …
根据以上规律,若≈1.30,≈4.11,则≈( )
A.13.0 B.130 C.41.1 D.411
6.若关于x的不等式5x+m≥7x的正整数解是1、2、3、4.则m的取值范围为( )
A.m<10 B.m≥8 C.8≤m≤10 D.8≤m<10
7.如图,下列条件不能判定CF∥BE的是( )
A.∠1=∠B B.∠1=∠C
C.∠CFB+∠B=180° D.∠CFP=∠FPB
8.若关于x的二次三项式4x2+(m﹣1)x+4是一个完全平方式,则m的值为( )
A.m=﹣7 B.m=9 C.m=5或m=﹣3 D.m=﹣7或m=9
9.如图,AB∥CD,FE⊥DB于点E,∠1=52°,则∠2的度数为( )
A.52° B.48° C.38° D.30°
10.如图,AB∥CD,EB⊥AB于点B,连接CE,若∠C=20°,则∠CEB=( )
A.120° B.115° C.100° D.110°
二、填空题(6小题,每题3分,共18分)
11.比较大小: .
12.已知2x+1的平方根为±5,则﹣5x﹣4的立方根是 .
13.若(m﹣2)x|m﹣1|﹣3>6是关于x的一元一次不等式,则m= .
14.若关于x的不等式组的解集是x>2,则m的取值范围是 .
15.若关于x,y的方程组的解满足0<x+y<1,则k的取值范围是 .
16.若2a=3,2b=6,2c=12,则a、b、c的关系:①c=a+2;②c﹣b=1;③a+c=2b;④a+b=c+1,其中正确的是 .
第II卷
湘教版2024—2025学年七年级下学期数学第三次月考考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
18.如果一个正数a的两个平方根是2x﹣2和6﹣3x.
求(1)x和这个正数a的值;
(2)17+3a的立方根.
19.如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)在网格中作出△ABC关于y轴对称的图形△A1B1C1;
(2)直接写出A1、B1、C1的坐标;
(3)若网格的单位长度为1,求△A1B1C1的面积.
20.如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN点PA、PB分别相交于点E、F,已知MN=8cm.
(1)求△OEF的周长;
(2)连接PM、PN,若∠APB=α,求∠MPN.(用含a的代数式表示)
21.有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t,5辆大货车与6辆小货车一次可以运货35t.
(1)3辆大货车与5辆小货车一次可以运货多少吨?
(2)计划用两种货车共12辆运输一批货物,大货车每次需运费3000元,小货车每次需运费1800元,若运输的总货物不少于38t,且总费用不超过32000元,请列出所有运输方案,并计算说明哪种方案所需费用最少,最少费用是多少?
22.已知方程组的解满足x为非正数,y为负数.
(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解集为x>1.
23.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
24.我们约定:若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“美美与共方程”,例如:方程x﹣2=2的解为x=4,而不等式组的解集为3<x<5,不难发现x=4在3<x<5的范围内,所以方程x﹣2=2是不等式组的“美美与共方程”.
(1)在一元一次方程①6x﹣7=4x﹣5;②2x+5=3(x﹣1);③中,不等式组的“美美与共方程”是 ;(填序号)
(2)若关于x的方程是不等式组的“美美与共方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“美美与共方程”,且此时该不等式组有7个整数解,若M=2m+3n﹣p,3m﹣n+p=4,m+n+p=6,求M的取值范围.
25.已知直线AB∥CD,直线EF与AB,CD分别交于点E,F,∠EFC=α(0°<α<90°).将一个直角三角板OPQ按如图1所示放置,使点Q,O分别在直线AB,CD上,∠P=90°,∠POQ=60°,∠PQO=30°,OP∥EF.
(1)若α=80°,分别求∠QOF与∠AQP的度数;
(2)求∠POC+∠AQP的度数;
(3)将直角三角板OPQ沿AB向右平移.
①如图2,当点Q与点E重合时,若EO恰好平分∠AEF,求α的值;
②作∠FOQ的平分线OG,交直线AB于点G,在整个平移过程中,直接写出∠AGO的度数(用含α 的式子表示).
参考答案
一、选择题
1—10:BCDBC BDDCD
二、填空题
11.【解答】解:∵
1,
∵1<3<4,
∴12,
∴1,
∴1<0,
∴.
故答案为:<.
12.【解答】解:由题意得:2x+1=25,
解得:x=12,
﹣5x﹣4=﹣5×12﹣4=﹣64,
﹣64的立方根是﹣4,
故答案为:﹣4.
13.【解答】解:根据题意,得
|m﹣1|=1且m﹣2≠0,
解得,m=0.
故答案为:0.
14.【解答】解:解x﹣1>1,得:x>2,
∵不等式组的解集是x>2,
∴m≤2,
故答案为:m≤2.
15.【解答】解:两方程相加得4x+4y=k+4,
∵0<x+y<1,
∴0<4x+4y<4,
则0<k+4<4,
解得﹣4<k<0,
故答案为:﹣4<k<0.
16.【解答】解:①②③.
三、解答题
17.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
18.【解答】解:(1)∵一个正数a的两个平方根是2x﹣2和6﹣3x,
∴2x﹣2+6﹣3x=0,
∴x=4.
∴2x﹣2=2×4﹣2=6,
∴a=36.
(2)∵a=36,
∴17+3a=17+3×36=125,
∵125的立方根为5,
∴17+3a的立方根为5.
19.【解答】解:(1)如图,△A1B1C1即为所求.
(2)A1(3,4),B1(5,2),C1(2,0);
(3)△A1B1C1的面积=3×41×42×22×3=5,
20.解:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF
=ME+EF+FN=MN
=8(cm);
(2)如图,连接PM,PN,PO,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2a.
21.解:(1)∵l1是AB边的垂直平分线,
14.【解答】解:(1)设1辆大货车一次运货xt,1辆小货车一次运货yt,
由题意得:,
解得:,
∴3x+5y=12+12.5=24.5t,
答:3辆大货车与5辆小货车一次可以运货24.5t;
(2)设用大货车a辆,则小货车(12﹣a)辆,总运费为z元,
由题意得:,
解得:5≤a≤8,
∴a的整数解有:6,7,8三个,
∴有3种运输方案,分别为:
方案一:大货车6辆,小货车6辆,
方案二:大货车7辆,小货车5辆,
方案三:大货车8辆,小货车4辆;
由题意得:z=3000a+1800(12﹣a)=1200a+21600,
当选方案一时:z=1200×6+21600=28800(元),
当选方案二时:z=1200×7+21600=30000(元),
当选方案三时:z=1200×8+21600=31200(元),
∵28800<30000<31200,
即选方案一费用最少,为28800元.
22.【解答】解:(1)解原方程组得:,
∵x≤0,y<0,
∴,
解得﹣2<m≤3;
(2)|m﹣3|﹣|m+2|=3﹣m﹣m﹣2=1﹣2m;
(3)解不等式2mx+x<2m+1得(2m+1)x<2m+1,
∵x>1,∴2m+1<0,
∴m,
∴﹣2<m,
∴m=﹣1.
23.【解答】解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
24.【解答】解:(1)①6x﹣7=4x﹣5,
解得x=1,
②2x+5=3(x﹣1),
解得x=8,
③,
解得x,
解不等式组,得x≤4,
由题:①③是不等式组的“美美与共方程”.
故答案为:①③;
(2)解关于x的方程,得x=2k+1,
解不等式组,得x,
由题意得:2k+1,
解得:k.
故k的取值范围是k;
(3)解方程,得x=2m﹣1,
解不等式组,得,
由题意得: ①,
且 ②,
解不等式①得:,
解不等式②得:3≤m<5,
∴3≤m≤4;
,
解得,
∴,
解得:19≤M≤26.
故M的取值范围是19≤M≤26
25.【解答】解:(1)如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∴∠OPQ=∠OPM+∠QOM=90°,
∵OP∥EF,
∴∠EFC=∠POC=α=80°,
∴∠AQP=90°﹣80°=10°,
∵AB∥CD,
∴∠QOF=∠AQO=∠AQP+∠PQO=10°+30°=40°,
即∠QOF=40°,∠AQP=10°;
(2)∠POC+∠AQP=90°,
如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∵∠OPQ=∠OPM+∠QOM=90°,
∴∠POC+∠AQP=90°;
(3)①如图2,∵EO恰好平分∠AEF,
∴∠AEO=∠OEF,
∵AB∥CD,
∴∠AEO=∠EOF=∠OEF,
∵OP∥EF,
∴∠POC=∠EFC=α,
∴∠EOF=180°﹣60°﹣α,
在△EOF中,由内角和定理可得,
∠EOF+∠OEF+∠OFE=180°,
即2×(180°﹣60°﹣α)+α=180°,
解得α=60°;
②如图1,∠AGO=∠GOF∠FOQ,
∵∠FOQ=180°﹣60°﹣α=120°﹣α,
∴∠AGO(120°﹣α)=60°α;
如图3,∵PO∥EF,
∴∠POF=∠EFC=α,
∴∠QOF=60°+α,
∵OG平分∠QOF,
∴∠GOF∠QOF=30°α,
∵AB∥CD,
∴∠AGO=180°﹣∠GOF=150°α,
综上所述∠AGO=150°α或∠AGO=60°α.
21世纪教育网(www.21cnjy.com)
同课章节目录
