湘教版2024—2025学年七年级下学期数学期末考试全真模拟试卷(含答案)
文档属性
| 名称 | 湘教版2024—2025学年七年级下学期数学期末考试全真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 558.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 10:02:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在﹣0.101001,,,,,0中,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
2.如图所示的图标中,不是轴对称图形的是( )
A. B. C. D.
3.在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交
C.平行或相交 D.平行、相交或垂直
4.若m>n,则下列结论正确的是( )
A.m+2<n+2 B.m﹣2<n﹣2 C.2m>2n D.﹣2m>﹣2n
5.若a2﹣b2=9,a+b=9,则a﹣b的值为( )
A.0 B.1 C.3 D.5
6.如图,四个图形中的∠1和∠2,不是同位角的是( )
A. B. C. D.
7.若实数a,b满足a2+b2=8,ab=4,则a+b的值为( )
A. B.4 C. D.±4
8.若a是大于1的正整数,且满足,则n的值是( )
A.5 B.6 C.7 D.8
9.若关于x的不等式组的解集只有3个整数解,则a的取值范围是( )
A.10<a≤12 B.10≤a<12 C.9≤a<10 D.9<a≤10
10.如图,将△ABC绕B点顺时针方向旋转到△DBE,点A的对应点D恰好落在AC上,且BE∥AC.若∠A=70°,则∠C的度数为( )
A.30° B.40° C.45° D.36°
二、填空题(6小题,每题3分,共18分)
11.八年(1)班学习委员调查本班学生一周内课外阅读情况,按照课外阅读时间进行统计,结果如表:
阅读时间 2小时以下 2﹣4小时 4小时以上
人数/名 25 15 a
百分比 b 30% 20%
则表中a的值是 .
12.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值为 .
13.如图,将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=34°,则∠DGH= .
14.若2m=3,2n=5,则22m+n= .
15.比较大小: .
16.若(m+1)x|m|﹣5>0是关于x的一元一次不等式,则m的值为 .
第II卷
湘教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组:.
18.先化简,再求值:[(x﹣2y)2﹣(x﹣2y)(x+2y)﹣2y(2x+4y)]÷2x,
其中|y+2|=0.
19.某正数的两个平方根分别是a+3和2a﹣15,b的立方根是﹣2.
(1)求a,b的值;
(2)求2a﹣b的算术平方根.
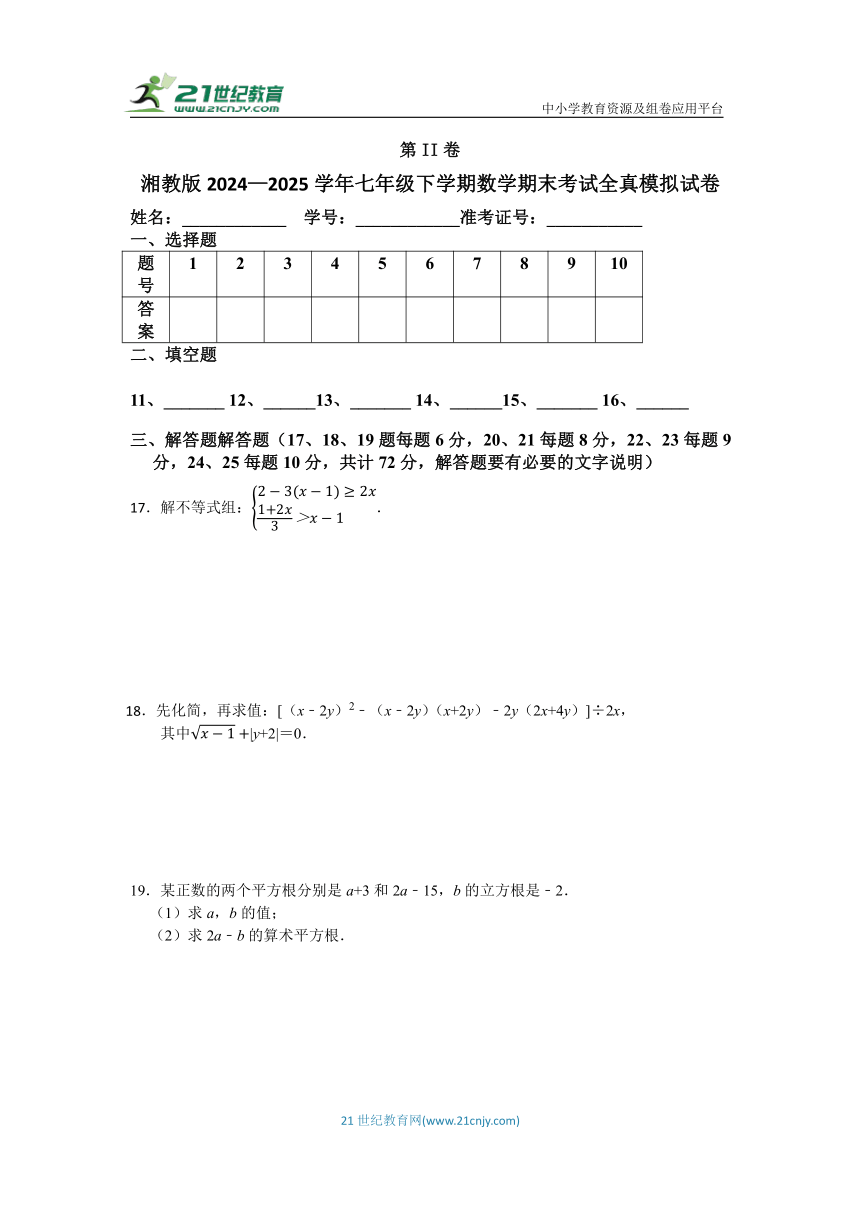
20.如图,已知∠1=48°,∠2=132°,∠C=∠D.
(1)求证:BD∥CE;
(2)若∠F=35°,求∠A的度数.
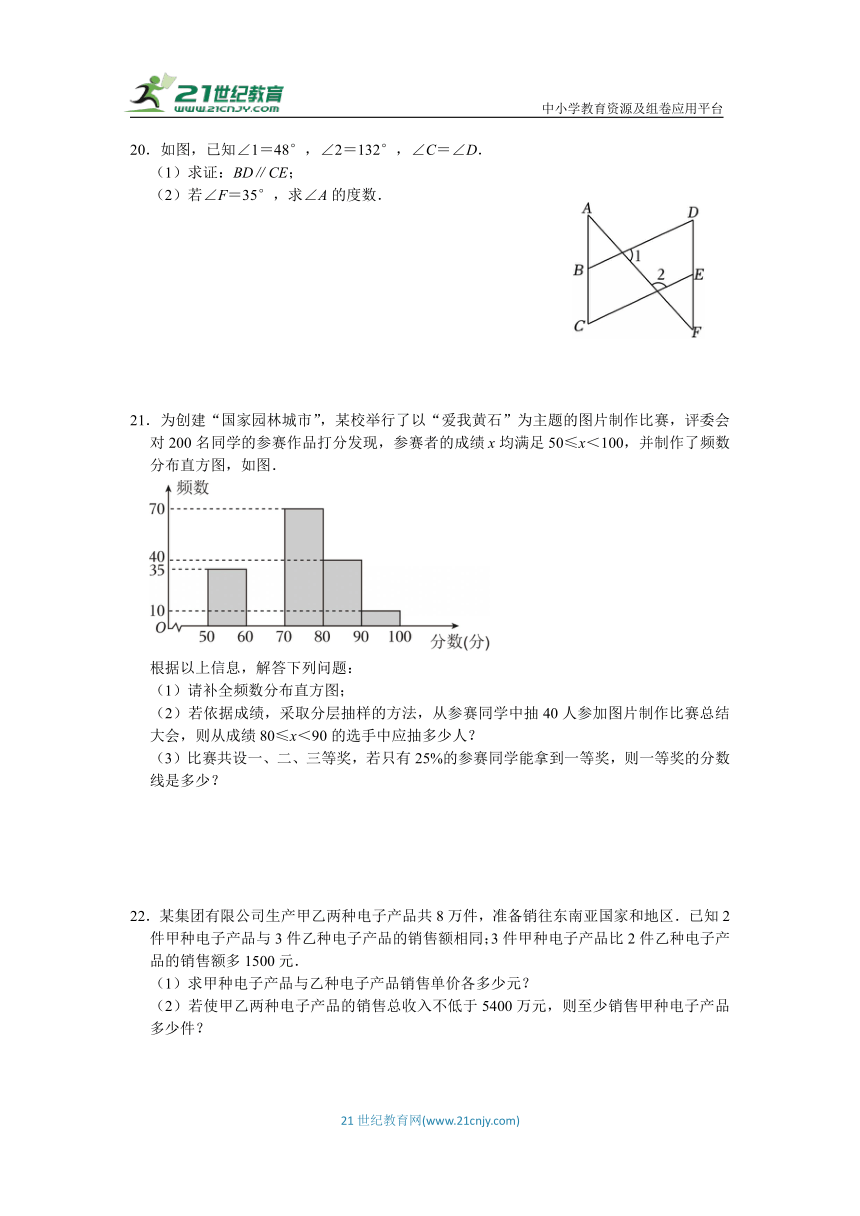
21.为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
22.某集团有限公司生产甲乙两种电子产品共8万件,准备销往东南亚国家和地区.已知2件甲种电子产品与3件乙种电子产品的销售额相同;3件甲种电子产品比2件乙种电子产品的销售额多1500元.
(1)求甲种电子产品与乙种电子产品销售单价各多少元?
(2)若使甲乙两种电子产品的销售总收入不低于5400万元,则至少销售甲种电子产品多少件?
23.已知:如图,AR∥CD,点B为CD上一点,∠A=∠C.
(1)如图1,求证:AB∥CR;
(2)如图2,点E为线段CR上一点,∠DBE的角平分线与∠ARC的角平分线相交于点H,请直接写出∠BHR与∠BER的数量关系,不必写出证明过程;
(3)如图3,在(2)的条件下,连接BR,且BR平分∠ABE,延长BE交AR的延长线于点F,过点F作FG⊥AF交线段BC于点G,FP平分∠BFG交线段HB的延长线于点P,若∠HRC=5∠HBR,∠BHR﹣2∠HPF=47°,求∠HRB的度数.
24.甲、乙两个长方形,它们的边长如图1所示,面积分别S1,S2(m为正整数).
(1)写出S1与S2的大小关系:S1 S2.(填“>”“<”或“=”);
(2)若|S1﹣S2|≤2025,求满足这个不等式的m的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为S3,S4的矩形恰好拼成一个矩形图案,如图2所示.问:是否存在m,使得2S3=S4,若存在,请求出m的值;若不存在,请说明理由.
25.【定义】若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“子方程”.例如:2x+4=2的解为的解集为﹣3≤x<4,不难发现x=﹣1在﹣3≤x<4的范围内,所以2x+4=2是的“子方程”.
【问题解决】(1)在方程①4x﹣5=x+7,②,③2x+3(x+2)=21中,不等式组的“子方程”是 (填序号);
(2)者关于x的方程2x﹣k=4是不等式组的“子方程”,求k的取值范围;
(3)若方程4x+4=0是关于x的不等式组的“子方程”,直接写出m的取值范围.
参考答案
一、选择题
1—10:BCCCB CDCAB
二、填空题
11.【解答】解:总人数为15÷30%=50(人),
∴a=50×20%=10.
故答案为:10.
12.【解答】解:如图,作点Q关于AD的对称点Q′,连接PQ′,CQ′,过点C作CH⊥AB于点H.
∵AD是△ABC的角平分线,Q与Q'关于AD对称,
∴点Q′在AB上,PC+PQ=PC+PQ′≥CH,
∵AC=3,BC=4,AB=5, AC BC AB CH,
∴CH=2.4,
∴CP+PQ≥2.4,
∴PC+PQ的最小值为2.4.
故答案为:2.4.
13.【解答】解:∵将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,
∴∠DGH=∠EGH,
∵∠AGE+∠EGH+∠DGH=180°,
∴2∠DGH=180°﹣∠AGE=180°﹣34°=146°,
∴∠DGH=73°,
故答案为:73°.
14.【解答】解:22m+n=(2m)2 2n=32×5=45.
故答案为:45.
15.【解答】解:∵,,18<12,
∴.
故答案为:>.
16.【解答】解:由条件可知|m|=1且m+1≠0,
∴m=1.
故答案为:1.
三、解答题
17.【解答】解:由不等式2﹣3(x﹣1)≥2x得:x≤1,
由不等式x﹣1得:x<4,
∴原不等式组的解集为x≤1.
18.【解答】解:[(x﹣2y)2﹣(x﹣2y)(x+2y)﹣2y(2x+4y)]÷2x
=(x2﹣4xy+4y2﹣x2+4y2﹣4xy﹣8y2)÷2x
=﹣8xy÷2x
=﹣4y,
∵|y+2|=0,
∴x﹣1=0,y+2=0,
∴x=1,y=﹣2,
当x=1 y=﹣2时,原式=﹣4×(﹣2)=8.
19.【解答】解:(1)∵某正数的两个平方根分别是a+3和2a﹣15,b的立方根是﹣2,
∴a+3+2a﹣15=0,b=(﹣2)3=﹣8,
解得,a=4,b=﹣8;
(2)∵a=4,b=﹣8,
∴2a﹣b=2×4﹣(﹣8)=16,
∵16的算术平方根是4,
∴2a﹣b的算术平方根是4.
20.【解答】(1)证明:∵∠1=48°,∠2=132°,
∴∠1+∠2=180°,
∴BD∥CE(同旁内角互补,两直线平行);
(2)解:∵BD∥CE(已证),
∴∠C=∠ABD(两直线平行,同位角相等).
又∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F=35°.
21.【解答】解:(1)200﹣(35+40+70+10)=45,如图:
(2)设抽了x人,则,解得x=8;
(3)依题意知获一等奖的人数为200×25%=50(人).
则一等奖的分数线是80分.
22.【解答】解:(1)设甲种电子产品的销售单价是x元,乙种电子产品的销售单价是y元,
根据题意得:,
解得:.
答:甲种电子产品的销售单价是900元,乙种电子产品的销售单价是600元;
(2)设销售甲种电子产品m万件,则销售乙种电子产品(8﹣m)万件,
根据题意得:900m+600(8﹣m)≥5400,
解得:m≥2,
∴m的最小值为2.
答:至少销售甲种电子产品2万件.
23.【解答】(1)证明:∵AR∥CD,
∴∠A=∠ABD,
∵∠A=∠C,
∴∠C=∠ABD,
∴AB∥CR;
(2)解:2∠BHR+∠BER=360°,理由如下:
如图:分别过点E,H作AR的平行线PQ,MN,
∵AR∥CD,AR∥PQ,AR∥MN,
∴AR∥MN∥PQ∥CD,
设∠ABD=x,∠ABH=y,则∠HBD=x+y,
∴∠C=x,∠BHN=x+y,
∴∠ARC=180°﹣x,∠PER=x,
∵BH平分∠DBE,RH平分∠ARC,
∴,
∴,
∴∠BEP=∠CBE=180°﹣2x﹣2y,
∴∠BEP=∠CBE=180°﹣2x﹣2y
∴,
∵2∠BHR=180°+x+2y,
∴2∠BHR+∠BER=180°+x+2y+180°﹣x﹣2y=360°;
(3)解:设∠HBR=α,∠ABH=β,则∠ABR=α+β,
∵BR平分∠ABE,
∴∠EBR=∠ABR=α+β,
∴∠HBE=∠HBR+∠EBR=2α+β,
∵BH平分∠DBE,
∴∠DBH=∠HBE=2α+β,
∴∠ABD=∠DBH﹣∠ABH=2α,
∴∠C=∠ABD=2α,
∵∠HRC=5∠HBR,
∴∠HRC=5α,
∵RH平分∠ARC,
∴∠ARH=∠HRC=5α,
∴∠CRF=180°﹣10α,
∵AR∥CD,
∴∠C=∠CRF,即2α=180°﹣10α,
∴α=15°,
∴∠C=∠CRF=30°,∠ARH=∠HRC=5α=75°,∠CBE=180°﹣2∠DBH=180°﹣4α﹣2β=120°﹣2β,
∴∠C=∠CRF=30°,
如图,过点P作PK∥CD,过点H作ST∥CD,
∴∠DBH=∠THB=2α+β=30°+β,∠THR=∠ARH=75°,
∴∠BHR=∠DBH+∠ARH=7α+β=105°+β,
∵∠CBH=180°﹣∠DBH=180°﹣2α﹣β=150°﹣β,
∴∠KPB=∠CBH=150°﹣β,
∵FG⊥AF,
∴∠AFG=90°,
∵AR∥CD,
∴∠CBE=∠AFB=120°﹣2β,
∴∠BFG=∠AFG﹣∠AFB=90°﹣(120°﹣2β)=2β﹣30°,
∵FP平分∠BFG,
∴,
∵AR∥CD,PK∥CD,
∴AR∥PK,
∴∠KPF=∠AFP=∠AFB+∠PFB=105°﹣β,
∴∠HPF=∠KPB﹣∠KPF=45°,
∵∠BHR﹣2∠HPF=47°,
∴105°+β﹣2×45°=47°,
∴β=32°,
∴∠DBR=∠DBH+∠HBR=2α+β+α=77°,
∴∠ARB=180°﹣∠DBR=180°﹣77°=103°,
∵∠ARH=75°,
∴∠HRB=∠ARB﹣∠ARH=103°﹣75°=28°,
所以∠HRB的度数为28°.
24.【解答】解:(1)S1=(m+7)(m+1)
=m2+m+7m+7
=m2+8m+7;
S2=(m+4)(m+2)
=m2+2m+4m+8
=m2+6m+8;
,
因为m为正整数,
所以2m﹣1>0,
所以S1>S2.
故答案为:>.
(2)因为S1﹣S2=2m﹣1,|S1﹣S2|≤2025,
即|2m﹣1|≤2025,
2m﹣1≤2025,
2m≤2026,
m≤1013.
所以m得最大值是1013.
(3)S3=[(m+4)×3+2m﹣9﹣(m+1)×4]×(m+7)
=(3m+12+2m﹣9﹣4m﹣4)×(m+7)
=(m﹣1)(m+7)
=m2+7m﹣m﹣7
=m2+6m﹣7;
S4=(2m﹣9)(m+2)
=2m2+4m﹣9m﹣18
=2m2﹣5m﹣18;
因为2S3=S4,
所以2×(m2+6m﹣7)=2m2﹣5m﹣18,
即2m2+12m﹣14=2m2﹣5m﹣18,
17m=﹣4,
,
因为m为正整数,
所以m 不存在.
25.【解答】解:(1)解方程4x﹣5=x+7得:x=4,
解方程得:,
解方程2x+3(x+2)=21得:x=3,
解不等式组得:3<x≤5,
所以不等式组 的“子方程”是①②.
故答案为:①②;
(2)解不等式5x﹣7>11﹣x,得:x>3,
解不等式2x≥3x﹣6,得:x≤6,
则不等式组的解集为3<x≤6,
解方程2x﹣k=4,得,
由题意,得,
∴6<k+4≤12,
解得:2<k≤8;
(3)解方程4x+4=0,得:x=﹣1,
解不等式组得:,
∴不等式组得解集为,
∴x=﹣1在范围内,
∴,
解得:m≤6.
21世纪教育网(www.21cnjy.com)
湘教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在﹣0.101001,,,,,0中,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
2.如图所示的图标中,不是轴对称图形的是( )
A. B. C. D.
3.在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交
C.平行或相交 D.平行、相交或垂直
4.若m>n,则下列结论正确的是( )
A.m+2<n+2 B.m﹣2<n﹣2 C.2m>2n D.﹣2m>﹣2n
5.若a2﹣b2=9,a+b=9,则a﹣b的值为( )
A.0 B.1 C.3 D.5
6.如图,四个图形中的∠1和∠2,不是同位角的是( )
A. B. C. D.
7.若实数a,b满足a2+b2=8,ab=4,则a+b的值为( )
A. B.4 C. D.±4
8.若a是大于1的正整数,且满足,则n的值是( )
A.5 B.6 C.7 D.8
9.若关于x的不等式组的解集只有3个整数解,则a的取值范围是( )
A.10<a≤12 B.10≤a<12 C.9≤a<10 D.9<a≤10
10.如图,将△ABC绕B点顺时针方向旋转到△DBE,点A的对应点D恰好落在AC上,且BE∥AC.若∠A=70°,则∠C的度数为( )
A.30° B.40° C.45° D.36°
二、填空题(6小题,每题3分,共18分)
11.八年(1)班学习委员调查本班学生一周内课外阅读情况,按照课外阅读时间进行统计,结果如表:
阅读时间 2小时以下 2﹣4小时 4小时以上
人数/名 25 15 a
百分比 b 30% 20%
则表中a的值是 .
12.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值为 .
13.如图,将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=34°,则∠DGH= .
14.若2m=3,2n=5,则22m+n= .
15.比较大小: .
16.若(m+1)x|m|﹣5>0是关于x的一元一次不等式,则m的值为 .
第II卷
湘教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组:.
18.先化简,再求值:[(x﹣2y)2﹣(x﹣2y)(x+2y)﹣2y(2x+4y)]÷2x,
其中|y+2|=0.
19.某正数的两个平方根分别是a+3和2a﹣15,b的立方根是﹣2.
(1)求a,b的值;
(2)求2a﹣b的算术平方根.
20.如图,已知∠1=48°,∠2=132°,∠C=∠D.
(1)求证:BD∥CE;
(2)若∠F=35°,求∠A的度数.
21.为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
22.某集团有限公司生产甲乙两种电子产品共8万件,准备销往东南亚国家和地区.已知2件甲种电子产品与3件乙种电子产品的销售额相同;3件甲种电子产品比2件乙种电子产品的销售额多1500元.
(1)求甲种电子产品与乙种电子产品销售单价各多少元?
(2)若使甲乙两种电子产品的销售总收入不低于5400万元,则至少销售甲种电子产品多少件?
23.已知:如图,AR∥CD,点B为CD上一点,∠A=∠C.
(1)如图1,求证:AB∥CR;
(2)如图2,点E为线段CR上一点,∠DBE的角平分线与∠ARC的角平分线相交于点H,请直接写出∠BHR与∠BER的数量关系,不必写出证明过程;
(3)如图3,在(2)的条件下,连接BR,且BR平分∠ABE,延长BE交AR的延长线于点F,过点F作FG⊥AF交线段BC于点G,FP平分∠BFG交线段HB的延长线于点P,若∠HRC=5∠HBR,∠BHR﹣2∠HPF=47°,求∠HRB的度数.
24.甲、乙两个长方形,它们的边长如图1所示,面积分别S1,S2(m为正整数).
(1)写出S1与S2的大小关系:S1 S2.(填“>”“<”或“=”);
(2)若|S1﹣S2|≤2025,求满足这个不等式的m的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为S3,S4的矩形恰好拼成一个矩形图案,如图2所示.问:是否存在m,使得2S3=S4,若存在,请求出m的值;若不存在,请说明理由.
25.【定义】若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“子方程”.例如:2x+4=2的解为的解集为﹣3≤x<4,不难发现x=﹣1在﹣3≤x<4的范围内,所以2x+4=2是的“子方程”.
【问题解决】(1)在方程①4x﹣5=x+7,②,③2x+3(x+2)=21中,不等式组的“子方程”是 (填序号);
(2)者关于x的方程2x﹣k=4是不等式组的“子方程”,求k的取值范围;
(3)若方程4x+4=0是关于x的不等式组的“子方程”,直接写出m的取值范围.
参考答案
一、选择题
1—10:BCCCB CDCAB
二、填空题
11.【解答】解:总人数为15÷30%=50(人),
∴a=50×20%=10.
故答案为:10.
12.【解答】解:如图,作点Q关于AD的对称点Q′,连接PQ′,CQ′,过点C作CH⊥AB于点H.
∵AD是△ABC的角平分线,Q与Q'关于AD对称,
∴点Q′在AB上,PC+PQ=PC+PQ′≥CH,
∵AC=3,BC=4,AB=5, AC BC AB CH,
∴CH=2.4,
∴CP+PQ≥2.4,
∴PC+PQ的最小值为2.4.
故答案为:2.4.
13.【解答】解:∵将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,
∴∠DGH=∠EGH,
∵∠AGE+∠EGH+∠DGH=180°,
∴2∠DGH=180°﹣∠AGE=180°﹣34°=146°,
∴∠DGH=73°,
故答案为:73°.
14.【解答】解:22m+n=(2m)2 2n=32×5=45.
故答案为:45.
15.【解答】解:∵,,18<12,
∴.
故答案为:>.
16.【解答】解:由条件可知|m|=1且m+1≠0,
∴m=1.
故答案为:1.
三、解答题
17.【解答】解:由不等式2﹣3(x﹣1)≥2x得:x≤1,
由不等式x﹣1得:x<4,
∴原不等式组的解集为x≤1.
18.【解答】解:[(x﹣2y)2﹣(x﹣2y)(x+2y)﹣2y(2x+4y)]÷2x
=(x2﹣4xy+4y2﹣x2+4y2﹣4xy﹣8y2)÷2x
=﹣8xy÷2x
=﹣4y,
∵|y+2|=0,
∴x﹣1=0,y+2=0,
∴x=1,y=﹣2,
当x=1 y=﹣2时,原式=﹣4×(﹣2)=8.
19.【解答】解:(1)∵某正数的两个平方根分别是a+3和2a﹣15,b的立方根是﹣2,
∴a+3+2a﹣15=0,b=(﹣2)3=﹣8,
解得,a=4,b=﹣8;
(2)∵a=4,b=﹣8,
∴2a﹣b=2×4﹣(﹣8)=16,
∵16的算术平方根是4,
∴2a﹣b的算术平方根是4.
20.【解答】(1)证明:∵∠1=48°,∠2=132°,
∴∠1+∠2=180°,
∴BD∥CE(同旁内角互补,两直线平行);
(2)解:∵BD∥CE(已证),
∴∠C=∠ABD(两直线平行,同位角相等).
又∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F=35°.
21.【解答】解:(1)200﹣(35+40+70+10)=45,如图:
(2)设抽了x人,则,解得x=8;
(3)依题意知获一等奖的人数为200×25%=50(人).
则一等奖的分数线是80分.
22.【解答】解:(1)设甲种电子产品的销售单价是x元,乙种电子产品的销售单价是y元,
根据题意得:,
解得:.
答:甲种电子产品的销售单价是900元,乙种电子产品的销售单价是600元;
(2)设销售甲种电子产品m万件,则销售乙种电子产品(8﹣m)万件,
根据题意得:900m+600(8﹣m)≥5400,
解得:m≥2,
∴m的最小值为2.
答:至少销售甲种电子产品2万件.
23.【解答】(1)证明:∵AR∥CD,
∴∠A=∠ABD,
∵∠A=∠C,
∴∠C=∠ABD,
∴AB∥CR;
(2)解:2∠BHR+∠BER=360°,理由如下:
如图:分别过点E,H作AR的平行线PQ,MN,
∵AR∥CD,AR∥PQ,AR∥MN,
∴AR∥MN∥PQ∥CD,
设∠ABD=x,∠ABH=y,则∠HBD=x+y,
∴∠C=x,∠BHN=x+y,
∴∠ARC=180°﹣x,∠PER=x,
∵BH平分∠DBE,RH平分∠ARC,
∴,
∴,
∴∠BEP=∠CBE=180°﹣2x﹣2y,
∴∠BEP=∠CBE=180°﹣2x﹣2y
∴,
∵2∠BHR=180°+x+2y,
∴2∠BHR+∠BER=180°+x+2y+180°﹣x﹣2y=360°;
(3)解:设∠HBR=α,∠ABH=β,则∠ABR=α+β,
∵BR平分∠ABE,
∴∠EBR=∠ABR=α+β,
∴∠HBE=∠HBR+∠EBR=2α+β,
∵BH平分∠DBE,
∴∠DBH=∠HBE=2α+β,
∴∠ABD=∠DBH﹣∠ABH=2α,
∴∠C=∠ABD=2α,
∵∠HRC=5∠HBR,
∴∠HRC=5α,
∵RH平分∠ARC,
∴∠ARH=∠HRC=5α,
∴∠CRF=180°﹣10α,
∵AR∥CD,
∴∠C=∠CRF,即2α=180°﹣10α,
∴α=15°,
∴∠C=∠CRF=30°,∠ARH=∠HRC=5α=75°,∠CBE=180°﹣2∠DBH=180°﹣4α﹣2β=120°﹣2β,
∴∠C=∠CRF=30°,
如图,过点P作PK∥CD,过点H作ST∥CD,
∴∠DBH=∠THB=2α+β=30°+β,∠THR=∠ARH=75°,
∴∠BHR=∠DBH+∠ARH=7α+β=105°+β,
∵∠CBH=180°﹣∠DBH=180°﹣2α﹣β=150°﹣β,
∴∠KPB=∠CBH=150°﹣β,
∵FG⊥AF,
∴∠AFG=90°,
∵AR∥CD,
∴∠CBE=∠AFB=120°﹣2β,
∴∠BFG=∠AFG﹣∠AFB=90°﹣(120°﹣2β)=2β﹣30°,
∵FP平分∠BFG,
∴,
∵AR∥CD,PK∥CD,
∴AR∥PK,
∴∠KPF=∠AFP=∠AFB+∠PFB=105°﹣β,
∴∠HPF=∠KPB﹣∠KPF=45°,
∵∠BHR﹣2∠HPF=47°,
∴105°+β﹣2×45°=47°,
∴β=32°,
∴∠DBR=∠DBH+∠HBR=2α+β+α=77°,
∴∠ARB=180°﹣∠DBR=180°﹣77°=103°,
∵∠ARH=75°,
∴∠HRB=∠ARB﹣∠ARH=103°﹣75°=28°,
所以∠HRB的度数为28°.
24.【解答】解:(1)S1=(m+7)(m+1)
=m2+m+7m+7
=m2+8m+7;
S2=(m+4)(m+2)
=m2+2m+4m+8
=m2+6m+8;
,
因为m为正整数,
所以2m﹣1>0,
所以S1>S2.
故答案为:>.
(2)因为S1﹣S2=2m﹣1,|S1﹣S2|≤2025,
即|2m﹣1|≤2025,
2m﹣1≤2025,
2m≤2026,
m≤1013.
所以m得最大值是1013.
(3)S3=[(m+4)×3+2m﹣9﹣(m+1)×4]×(m+7)
=(3m+12+2m﹣9﹣4m﹣4)×(m+7)
=(m﹣1)(m+7)
=m2+7m﹣m﹣7
=m2+6m﹣7;
S4=(2m﹣9)(m+2)
=2m2+4m﹣9m﹣18
=2m2﹣5m﹣18;
因为2S3=S4,
所以2×(m2+6m﹣7)=2m2﹣5m﹣18,
即2m2+12m﹣14=2m2﹣5m﹣18,
17m=﹣4,
,
因为m为正整数,
所以m 不存在.
25.【解答】解:(1)解方程4x﹣5=x+7得:x=4,
解方程得:,
解方程2x+3(x+2)=21得:x=3,
解不等式组得:3<x≤5,
所以不等式组 的“子方程”是①②.
故答案为:①②;
(2)解不等式5x﹣7>11﹣x,得:x>3,
解不等式2x≥3x﹣6,得:x≤6,
则不等式组的解集为3<x≤6,
解方程2x﹣k=4,得,
由题意,得,
∴6<k+4≤12,
解得:2<k≤8;
(3)解方程4x+4=0,得:x=﹣1,
解不等式组得:,
∴不等式组得解集为,
∴x=﹣1在范围内,
∴,
解得:m≤6.
21世纪教育网(www.21cnjy.com)
同课章节目录
