青岛版2024—2025学年八年级下学期数学期末考试模拟试卷(含答案)
文档属性
| 名称 | 青岛版2024—2025学年八年级下学期数学期末考试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 391.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 10:01:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
青岛版2024—2025学年八年级下学期数学期末考试模拟试卷
满分:120分 时间:120分钟 范围:第一章平行四边形到第五章一次函数
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50° B.80° C.100° D.130°
2.若m与m﹣2是同一个正数的两个平方根,则m的值为( )
A.﹣2 B.﹣1 C.1 D.2
3.估计的值在( )
A.4到5之间 B.3到4之间 C.2到3之间 D.1到2之间
4.下列说法正确的是( )
A.菱形的四个内角都是直角
B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角
D.平行四边形是轴对称图形
5.已知关于x的不等式(1+2a)x>1的解集为,则a的取值范围是( )
A. B. C. D.
6.已知a,b2,则a,b的关系是( )
A.a=b B.a=﹣b C.a D.ab=﹣1
7.已知实数a满足条件|2023﹣a|a,那么a﹣20232的值为( )
A.2021 B.2022 C.2023 D.2024
8.若关于y的不等式组有解,则满足条件的整数m的最大值为( )
A.6 B.7 C.8 D.9
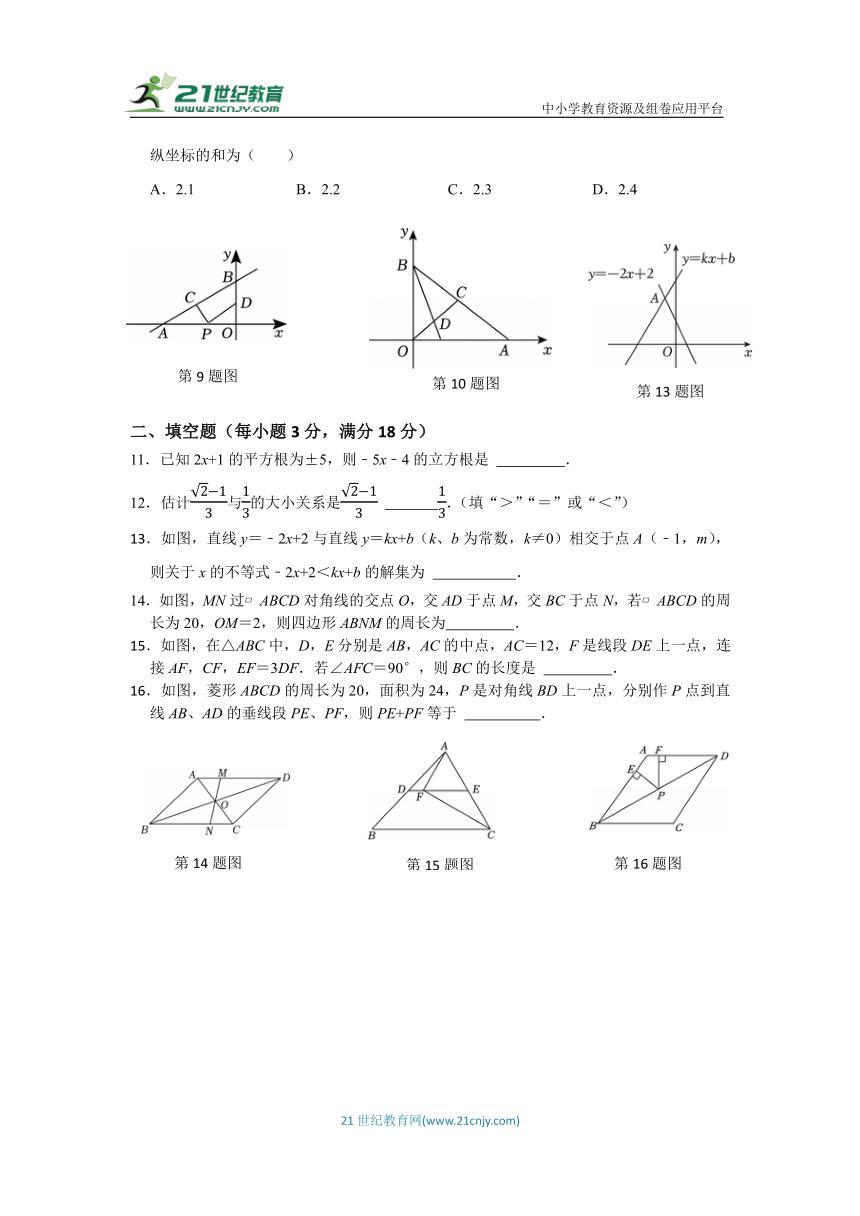
9.如图,直线与x轴,y轴分别交于点A和点B,点C在线段AB上,且点C坐标为(m,2),点D为线段OB的中点,点P为OA上一动点,当△PCD的周长最小时,点P的坐标为( )
A.(﹣3,0) B. C. D.
10.如图,已知一次函数的图象与x轴交于点A,与y轴交于点B,点C在线段AB上,且OC=2.4,直线OC与∠OBA的平分线交于D点,则点D的横坐标与它的纵坐标的和为( )
A.2.1 B.2.2 C.2.3 D.2.4
二、填空题(每小题3分,满分18分)
11.已知2x+1的平方根为±5,则﹣5x﹣4的立方根是 .
12.估计与的大小关系是 .(填“>”“=”或“<”)
13.如图,直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),则关于x的不等式﹣2x+2<kx+b的解集为 .
14.如图,MN过 ABCD对角线的交点O,交AD于点M,交BC于点N,若 ABCD的周长为20,OM=2,则四边形ABNM的周长为 .
15.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是线段DE上一点,连接AF,CF,EF=3DF.若∠AFC=90°,则BC的长度是 .
16.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
青岛版2024—2025学年八年级下学期数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.已知实数a,b的对应点在数轴上的位置如图所示.
(1)判断正负,用“>”“<”填空:b+a 0,﹣a+b 0.
(2)化简:.
19.解不等式组:.
20.某初中购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
21.如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,连接CD,过点C作CE∥AB,过点A作AE∥CD,CE,AE交于点E,连接DE交AC于点O.
(1)求证:四边形AECD是菱形;
(2)连接BE交AC于点F,交CD于点G,若DE=CE,CD=2,求OF的长.
22.已知关于a、b的方程组中,a为负数,b为非正数.
(1)求m的取值范围;
(2)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解集为x>1.
23.某市自来水公司为了鼓励市民节约用水,水费按分段收费标准收取.居民每月应交水费y(元)与用水量x(吨)之间的函数关系如图所示.请你观察函数图象,回答下列相关问题.
(1)若用水不超过10吨,水费为 元/吨.
(2)求出居民每月应交水费y(元)与用水量x(吨)之间的函数关系式.
(3)若某户居民8月共交水费65元,求该户居民8月共用水多少吨?
24.如图(1),在平面直角坐标系中,直线y=kx+6k(k是常数,k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,8).
(1)求点A的坐标;
(2)P是x轴上一点,已知∠ABP=45°,求点P的坐标;
(3)如图(2),已知AC平分∠BAO,D为AB的中点.
①请直接写出直线CD的解析式;
②点M在直线CD上,在x轴上取点N,使以M、A、N、B为顶点的四边形是平行四边形,请直接写出点N的坐标.
25.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过(﹣3,12),(6,0)两点,与x轴和y轴分别交于点A和点B.
(1)求一次函数y=kx+b的解析式;
(2)若点P在线段AB上,过P点作PC⊥OA于点C,作PD⊥OB于点D,若四边形PCOD为正方形,求点P的坐标;
(3)点M在x轴上,点N在第一象限,若以A,B,M,N为顶点的四边形是菱形,直接写出点N的坐标.
参考答案
一、选择题
1—10:DCCCB BDBBA
二、填空题
11.【解答】解:由题意得:2x+1=25,
解得:x=12,
﹣5x﹣4=﹣5×12﹣4=﹣64,
﹣64的立方根是﹣4,
故答案为:﹣4.
12.【解答】解:∵,
,
∴,
∴.
故答案为:<.
13.【解答】解:∵直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),
∴x>﹣1时,﹣2x+2<kx+b.
∴关于x的不等式﹣2x+2<kx+b的解集为x>﹣1.
故答案为:x>﹣1.
14.【解答】解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAM=∠OCN,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴OM=ON=2,AM=CN,
则四边形ABNM的周长=BN+AB+AM+MN=(BN+AM)+AB+MN=BC+AB+MN=10+4=14.
故答案为:14.
15.【解答】解:∵∠AFC=90°,
∴△AFC是直角三角形,
∵点E为AC的中点,AC=12,
∴,
∵F是线段DE上一点,连接AF,CF,EF=3DF,
∴,
∴DE=DF+EF=8,
∵D,E分别是AB,AC的中点,
∴DE是△ABC中位线,
∴BC=2DE=16,
故答案为:16.
16.【解答】解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
17.【解答】解:(1)
;
(2)
=41
=41+1
.
18.【解答】解:(1)由数轴得:﹣1<a<0,0<b<1,|b|>|a|,
∴b+a>0,﹣a+b>0;
故答案为:>,>;
(2)由数轴得:﹣1<a<0,0<b<1,|b|>|a|,
∴a+1>0,b﹣1<0,a﹣b<0,
∴
=a+1+2(1﹣b)+(b﹣a)
=a+1+2﹣2b+b﹣a
=3﹣b.
19.【解答】解:由不等式2﹣3(x﹣1)≥2x得:x≤1,
由不等式x﹣1得:x<4,
∴原不等式组的解集为x≤1.
20.【解答】解:(1)设每个A种徽章的价格为x元,每个B种徽章的价格为y元,
由题意得:,
解得:,
答:每个A种价格为36元,每个B种价格分别为28元;
(2)设购进m个A种徽章,则:
,
∴,
∴m=40,
答:购进A种徽章的个数是40.
21.【解答】(1)证明:∵∠ACB=90°,点D是AB中点,
∴,
∵AE∥CD,CE∥AB,
∴四边形AECD是平行四边形,
∵CD=AD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AC⊥DE,CD=CE,OD=OE,
∵DE=CE,CD=2,
∴DE=CE=CD=2,△CDE为等边三角形,
∴∠AOD=∠ACB=90°,OD=OE=1,∠DEC=60°,
∴BC∥DE,
∵CE∥BD,
∴四边形BCED是平行四边形,
∵DE=CE,
∴四边形BCED是菱形,
∴,
∴EF=2OF,
由勾股定理得OF2=EF2﹣OE2,即OF2=(2OF)2﹣12,
解得.
22.【解答】解:(1),
(①+②)÷2得:a=m﹣3③,
将③代入②得:﹣3+m+b=﹣7﹣m,
解得:b=﹣2m﹣4,
∴方程组的解为.
∵a为负数,b为非正数,
∴,
解得:﹣2≤m<3,
∴m的取值范围为﹣2≤m<3;
(2)∵2mx+x<2m+1,
∴(2m+1)x<2m+1.
∵不等式2mx+x<2m+1的解集为x>1,
∴2m+1<0,
∴m,
∵﹣2≤m<3,
∴﹣2≤m,
∴m=﹣1或m=﹣2,
∴当m为﹣2或﹣1时,不等式2mx+x<2m+1的解集为x>1.
23.【解答】解:(1)由图象可得,
若用水不超过10吨,水费为25÷10=2.5(元/吨),
故答案为:2.5;
(2)当0≤x≤10时,设y与x的函数解析式为y=kx,
∵点(10,25)在该函数图象上,
∴25=10k,
解得k=2.5,
即当0≤x≤10时,y与x的函数解析式为y=2.5x;
当x>10时,设y与x的函数解析式为y=ax+b,
则,
解得,
即当x>10时,y与x的函数解析式为y=4x﹣15;
由上可得,y与x的函数解析式为y;
(3)将y=65代入y=4x﹣15,得:65=4x﹣15,
解得x=20,
答:该户居民8月共用水20吨.
24.【解答】解:(1)∵直线 y=kx+6k过点B(0,8),
∴6k=8,
解得k,
∴直线AB解析式为yx+8,
令y=0,则 ,
解得x=﹣6,
∴A(﹣6,0);
(2)①当P在点A右侧时,过点A作AD⊥AB,AD=AB,连接BD,则BD与x轴的交点即为点P.过点D作DE⊥x轴于点E,则∠BOA=∠AED=∠BAD=90°,如图:
∴∠ABO+∠BAO=∠DAE+∠BAO=90°,
∴∠ABO=∠DAE,
∴△ABO≌△DAE(AAS),
∴AE=OB=8,DE=OA=6,
∴D(2,﹣6),
由B(0,8),D(2,﹣6)得直线BD解析式为y=﹣7x+8,
令y=0,则﹣7x+8=0,
∴解得x,
∴P(,0);
②当P在点A左侧时,过点A作AC⊥AB,AC=AB,连接BC,则BC与x轴的交点即为点P,
同理可得C(﹣14,6),
由B(0,8),C(﹣14,6)可得直线BC的解析式为yx+8;
令y=0,则,
∴x=﹣56,
∴P(﹣56,0),
综上所述,P的坐标为(,0)或(﹣56,0);
(3)①过C作CH⊥AB于H,如图:
∵A(﹣6,0),B(0,8),D为AB中点,
∴AB10,D(﹣3,4),
∵AC平分∠BAO,
∴∠HAC=∠OAC,
∵∠AHC=90°=∠AOC,AC=AC,
∴△ACH≌△ACO(AAS),
∴CH=CO,AH=OA=6,
∴BH=AB﹣AH=10﹣6=4,
设OC=t,则BC=8﹣t,
∵BH2+CH2=BC2,
∴42+t2=(8﹣t)2,
解得t=3,
∴C(0,3),
设直线CD解析式为y=kx+b,把C(0,3),D(﹣3,4)代入得:
,
解得,
∴直线CD解析式为yx+3;
②设M(m,m+3),N(n,0),
又A(﹣6,0),B(0,8),
当MN,AB为对角线时,MN,AB的中点重合,
∴,
解得,
∴N(9,0);
当MA,NB为对角线时,MA,NB的中点重合,
,
解得,
∴N(﹣21,0);
当MB,NA为对角线时,MB,NA的中点重合,
∴,
解得,
∴N(39,0);
综上所述,N的坐标为(﹣21,0)或(9,0)或(39,0).
25.【解答】解:(1)把(﹣3,12),(6,0)代入y=kx+b得,,
解得,
∴一次函数y=kx+b的解析式为yx+8;
(2)∵四边形PCOD为正方形,
∴PD=PC,
设P(m,n),
∴m=n,
把P(m,n)代入yx+8得,,
解得m=n,
∴点P的坐标为(,);
(3)在yx+8中,令x=0,则y=8,令y=0,则x=6,
∴A(6,0),B(0,8),
∴AB10,
由题意得点M在x轴上,点N在第一象限内,以A,B,M,N为顶点的四边形是菱形,
所以可分两种情况讨论:
①当AB为菱形的边长,
此时BN=BA=10,
∴N(10,8);
②当AB为菱形对角线时,
此时设BM=AM=a,
∴OM=AM﹣OA=a﹣6,
在Rt△BOM中,OB2+OM2=BM2,
即64+(a﹣6)2=a2,
解得a,
∴BN=BM,
∴N(,8);
综上所述,N(10,8)或(,8).
21世纪教育网(www.21cnjy.com)
青岛版2024—2025学年八年级下学期数学期末考试模拟试卷
满分:120分 时间:120分钟 范围:第一章平行四边形到第五章一次函数
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50° B.80° C.100° D.130°
2.若m与m﹣2是同一个正数的两个平方根,则m的值为( )
A.﹣2 B.﹣1 C.1 D.2
3.估计的值在( )
A.4到5之间 B.3到4之间 C.2到3之间 D.1到2之间
4.下列说法正确的是( )
A.菱形的四个内角都是直角
B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角
D.平行四边形是轴对称图形
5.已知关于x的不等式(1+2a)x>1的解集为,则a的取值范围是( )
A. B. C. D.
6.已知a,b2,则a,b的关系是( )
A.a=b B.a=﹣b C.a D.ab=﹣1
7.已知实数a满足条件|2023﹣a|a,那么a﹣20232的值为( )
A.2021 B.2022 C.2023 D.2024
8.若关于y的不等式组有解,则满足条件的整数m的最大值为( )
A.6 B.7 C.8 D.9
9.如图,直线与x轴,y轴分别交于点A和点B,点C在线段AB上,且点C坐标为(m,2),点D为线段OB的中点,点P为OA上一动点,当△PCD的周长最小时,点P的坐标为( )
A.(﹣3,0) B. C. D.
10.如图,已知一次函数的图象与x轴交于点A,与y轴交于点B,点C在线段AB上,且OC=2.4,直线OC与∠OBA的平分线交于D点,则点D的横坐标与它的纵坐标的和为( )
A.2.1 B.2.2 C.2.3 D.2.4
二、填空题(每小题3分,满分18分)
11.已知2x+1的平方根为±5,则﹣5x﹣4的立方根是 .
12.估计与的大小关系是 .(填“>”“=”或“<”)
13.如图,直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),则关于x的不等式﹣2x+2<kx+b的解集为 .
14.如图,MN过 ABCD对角线的交点O,交AD于点M,交BC于点N,若 ABCD的周长为20,OM=2,则四边形ABNM的周长为 .
15.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是线段DE上一点,连接AF,CF,EF=3DF.若∠AFC=90°,则BC的长度是 .
16.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
青岛版2024—2025学年八年级下学期数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.已知实数a,b的对应点在数轴上的位置如图所示.
(1)判断正负,用“>”“<”填空:b+a 0,﹣a+b 0.
(2)化简:.
19.解不等式组:.
20.某初中购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
21.如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,连接CD,过点C作CE∥AB,过点A作AE∥CD,CE,AE交于点E,连接DE交AC于点O.
(1)求证:四边形AECD是菱形;
(2)连接BE交AC于点F,交CD于点G,若DE=CE,CD=2,求OF的长.
22.已知关于a、b的方程组中,a为负数,b为非正数.
(1)求m的取值范围;
(2)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解集为x>1.
23.某市自来水公司为了鼓励市民节约用水,水费按分段收费标准收取.居民每月应交水费y(元)与用水量x(吨)之间的函数关系如图所示.请你观察函数图象,回答下列相关问题.
(1)若用水不超过10吨,水费为 元/吨.
(2)求出居民每月应交水费y(元)与用水量x(吨)之间的函数关系式.
(3)若某户居民8月共交水费65元,求该户居民8月共用水多少吨?
24.如图(1),在平面直角坐标系中,直线y=kx+6k(k是常数,k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,8).
(1)求点A的坐标;
(2)P是x轴上一点,已知∠ABP=45°,求点P的坐标;
(3)如图(2),已知AC平分∠BAO,D为AB的中点.
①请直接写出直线CD的解析式;
②点M在直线CD上,在x轴上取点N,使以M、A、N、B为顶点的四边形是平行四边形,请直接写出点N的坐标.
25.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过(﹣3,12),(6,0)两点,与x轴和y轴分别交于点A和点B.
(1)求一次函数y=kx+b的解析式;
(2)若点P在线段AB上,过P点作PC⊥OA于点C,作PD⊥OB于点D,若四边形PCOD为正方形,求点P的坐标;
(3)点M在x轴上,点N在第一象限,若以A,B,M,N为顶点的四边形是菱形,直接写出点N的坐标.
参考答案
一、选择题
1—10:DCCCB BDBBA
二、填空题
11.【解答】解:由题意得:2x+1=25,
解得:x=12,
﹣5x﹣4=﹣5×12﹣4=﹣64,
﹣64的立方根是﹣4,
故答案为:﹣4.
12.【解答】解:∵,
,
∴,
∴.
故答案为:<.
13.【解答】解:∵直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),
∴x>﹣1时,﹣2x+2<kx+b.
∴关于x的不等式﹣2x+2<kx+b的解集为x>﹣1.
故答案为:x>﹣1.
14.【解答】解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAM=∠OCN,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴OM=ON=2,AM=CN,
则四边形ABNM的周长=BN+AB+AM+MN=(BN+AM)+AB+MN=BC+AB+MN=10+4=14.
故答案为:14.
15.【解答】解:∵∠AFC=90°,
∴△AFC是直角三角形,
∵点E为AC的中点,AC=12,
∴,
∵F是线段DE上一点,连接AF,CF,EF=3DF,
∴,
∴DE=DF+EF=8,
∵D,E分别是AB,AC的中点,
∴DE是△ABC中位线,
∴BC=2DE=16,
故答案为:16.
16.【解答】解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
17.【解答】解:(1)
;
(2)
=41
=41+1
.
18.【解答】解:(1)由数轴得:﹣1<a<0,0<b<1,|b|>|a|,
∴b+a>0,﹣a+b>0;
故答案为:>,>;
(2)由数轴得:﹣1<a<0,0<b<1,|b|>|a|,
∴a+1>0,b﹣1<0,a﹣b<0,
∴
=a+1+2(1﹣b)+(b﹣a)
=a+1+2﹣2b+b﹣a
=3﹣b.
19.【解答】解:由不等式2﹣3(x﹣1)≥2x得:x≤1,
由不等式x﹣1得:x<4,
∴原不等式组的解集为x≤1.
20.【解答】解:(1)设每个A种徽章的价格为x元,每个B种徽章的价格为y元,
由题意得:,
解得:,
答:每个A种价格为36元,每个B种价格分别为28元;
(2)设购进m个A种徽章,则:
,
∴,
∴m=40,
答:购进A种徽章的个数是40.
21.【解答】(1)证明:∵∠ACB=90°,点D是AB中点,
∴,
∵AE∥CD,CE∥AB,
∴四边形AECD是平行四边形,
∵CD=AD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AC⊥DE,CD=CE,OD=OE,
∵DE=CE,CD=2,
∴DE=CE=CD=2,△CDE为等边三角形,
∴∠AOD=∠ACB=90°,OD=OE=1,∠DEC=60°,
∴BC∥DE,
∵CE∥BD,
∴四边形BCED是平行四边形,
∵DE=CE,
∴四边形BCED是菱形,
∴,
∴EF=2OF,
由勾股定理得OF2=EF2﹣OE2,即OF2=(2OF)2﹣12,
解得.
22.【解答】解:(1),
(①+②)÷2得:a=m﹣3③,
将③代入②得:﹣3+m+b=﹣7﹣m,
解得:b=﹣2m﹣4,
∴方程组的解为.
∵a为负数,b为非正数,
∴,
解得:﹣2≤m<3,
∴m的取值范围为﹣2≤m<3;
(2)∵2mx+x<2m+1,
∴(2m+1)x<2m+1.
∵不等式2mx+x<2m+1的解集为x>1,
∴2m+1<0,
∴m,
∵﹣2≤m<3,
∴﹣2≤m,
∴m=﹣1或m=﹣2,
∴当m为﹣2或﹣1时,不等式2mx+x<2m+1的解集为x>1.
23.【解答】解:(1)由图象可得,
若用水不超过10吨,水费为25÷10=2.5(元/吨),
故答案为:2.5;
(2)当0≤x≤10时,设y与x的函数解析式为y=kx,
∵点(10,25)在该函数图象上,
∴25=10k,
解得k=2.5,
即当0≤x≤10时,y与x的函数解析式为y=2.5x;
当x>10时,设y与x的函数解析式为y=ax+b,
则,
解得,
即当x>10时,y与x的函数解析式为y=4x﹣15;
由上可得,y与x的函数解析式为y;
(3)将y=65代入y=4x﹣15,得:65=4x﹣15,
解得x=20,
答:该户居民8月共用水20吨.
24.【解答】解:(1)∵直线 y=kx+6k过点B(0,8),
∴6k=8,
解得k,
∴直线AB解析式为yx+8,
令y=0,则 ,
解得x=﹣6,
∴A(﹣6,0);
(2)①当P在点A右侧时,过点A作AD⊥AB,AD=AB,连接BD,则BD与x轴的交点即为点P.过点D作DE⊥x轴于点E,则∠BOA=∠AED=∠BAD=90°,如图:
∴∠ABO+∠BAO=∠DAE+∠BAO=90°,
∴∠ABO=∠DAE,
∴△ABO≌△DAE(AAS),
∴AE=OB=8,DE=OA=6,
∴D(2,﹣6),
由B(0,8),D(2,﹣6)得直线BD解析式为y=﹣7x+8,
令y=0,则﹣7x+8=0,
∴解得x,
∴P(,0);
②当P在点A左侧时,过点A作AC⊥AB,AC=AB,连接BC,则BC与x轴的交点即为点P,
同理可得C(﹣14,6),
由B(0,8),C(﹣14,6)可得直线BC的解析式为yx+8;
令y=0,则,
∴x=﹣56,
∴P(﹣56,0),
综上所述,P的坐标为(,0)或(﹣56,0);
(3)①过C作CH⊥AB于H,如图:
∵A(﹣6,0),B(0,8),D为AB中点,
∴AB10,D(﹣3,4),
∵AC平分∠BAO,
∴∠HAC=∠OAC,
∵∠AHC=90°=∠AOC,AC=AC,
∴△ACH≌△ACO(AAS),
∴CH=CO,AH=OA=6,
∴BH=AB﹣AH=10﹣6=4,
设OC=t,则BC=8﹣t,
∵BH2+CH2=BC2,
∴42+t2=(8﹣t)2,
解得t=3,
∴C(0,3),
设直线CD解析式为y=kx+b,把C(0,3),D(﹣3,4)代入得:
,
解得,
∴直线CD解析式为yx+3;
②设M(m,m+3),N(n,0),
又A(﹣6,0),B(0,8),
当MN,AB为对角线时,MN,AB的中点重合,
∴,
解得,
∴N(9,0);
当MA,NB为对角线时,MA,NB的中点重合,
,
解得,
∴N(﹣21,0);
当MB,NA为对角线时,MB,NA的中点重合,
∴,
解得,
∴N(39,0);
综上所述,N的坐标为(﹣21,0)或(9,0)或(39,0).
25.【解答】解:(1)把(﹣3,12),(6,0)代入y=kx+b得,,
解得,
∴一次函数y=kx+b的解析式为yx+8;
(2)∵四边形PCOD为正方形,
∴PD=PC,
设P(m,n),
∴m=n,
把P(m,n)代入yx+8得,,
解得m=n,
∴点P的坐标为(,);
(3)在yx+8中,令x=0,则y=8,令y=0,则x=6,
∴A(6,0),B(0,8),
∴AB10,
由题意得点M在x轴上,点N在第一象限内,以A,B,M,N为顶点的四边形是菱形,
所以可分两种情况讨论:
①当AB为菱形的边长,
此时BN=BA=10,
∴N(10,8);
②当AB为菱形对角线时,
此时设BM=AM=a,
∴OM=AM﹣OA=a﹣6,
在Rt△BOM中,OB2+OM2=BM2,
即64+(a﹣6)2=a2,
解得a,
∴BN=BM,
∴N(,8);
综上所述,N(10,8)或(,8).
21世纪教育网(www.21cnjy.com)
同课章节目录
