第二十二章 二次函数 练习(含答案)人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 练习(含答案)人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 445.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览




文档简介
第二十二章 二次函数 练习
一、选择题
1.下列函数属于二次函数的是( ).
A. B.
C. D.
2.二次函数的图象的顶点坐标是( )
A. B. C. D.
3.抛物线先向左平移2个单位长度,再向下平移5个单位长度得到的抛物线的表达式是( )
A. B. C. D.
4.若抛物线经过点,则下列各点,必在抛物线上的是( )
A. B. C. D.
5.二次函数的图象如图所示,反比例函数与正比例函数在同一坐标系内的大致图象是( )
A. B.
C. D.
6.已知二次函数的图象如图所示,该抛物线的对称轴为直线,则下列结论不正确的是( )
A.
B.关于x的方程的两根是
C.当时,y随x的增大而减小
D.
7.已知二次函数y=x2-4x+2,在-1≤x≤3的取值范围内,下列关于该函数的说法中正确的是( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
8.已知点、的坐标分别为、,抛物线的顶点在线段上,抛物线与轴交于、两点(在的左侧),若四边形为平行四边形,则的值为( )
A. B. C. D.
9.如图,正的边长为4,点P为边上的任意一点(不与点B、C重合),且,交于点D.设,,则y关于x的函数图象大致是( )
A. B.
C. D.
10.如图,和都是等腰直角三角形,,,,点A,C,E共线,点F和点G分别是和的中点,,连接,下列结论错误的是( )
A.的最小值是2 B.的最大值为1
C.的最小值为 D.的最小值为
二、填空题
11.当 时,函数是二次函数.
12.把二次函数,化成的形式是 .
13.已知,在二次函数的图象上,比较 .(填、或)
14.如图,将抛物线沿y轴向下平移一段距离后,得到一条新的抛物线;若曲线段平移至曲线段,曲线段所扫过的为阴影部分,则阴影部分的面积是 .
15.已知二次函数(为常数)的图象与轴有交点,且当时,随的增大而增大,则的取值范围是 .
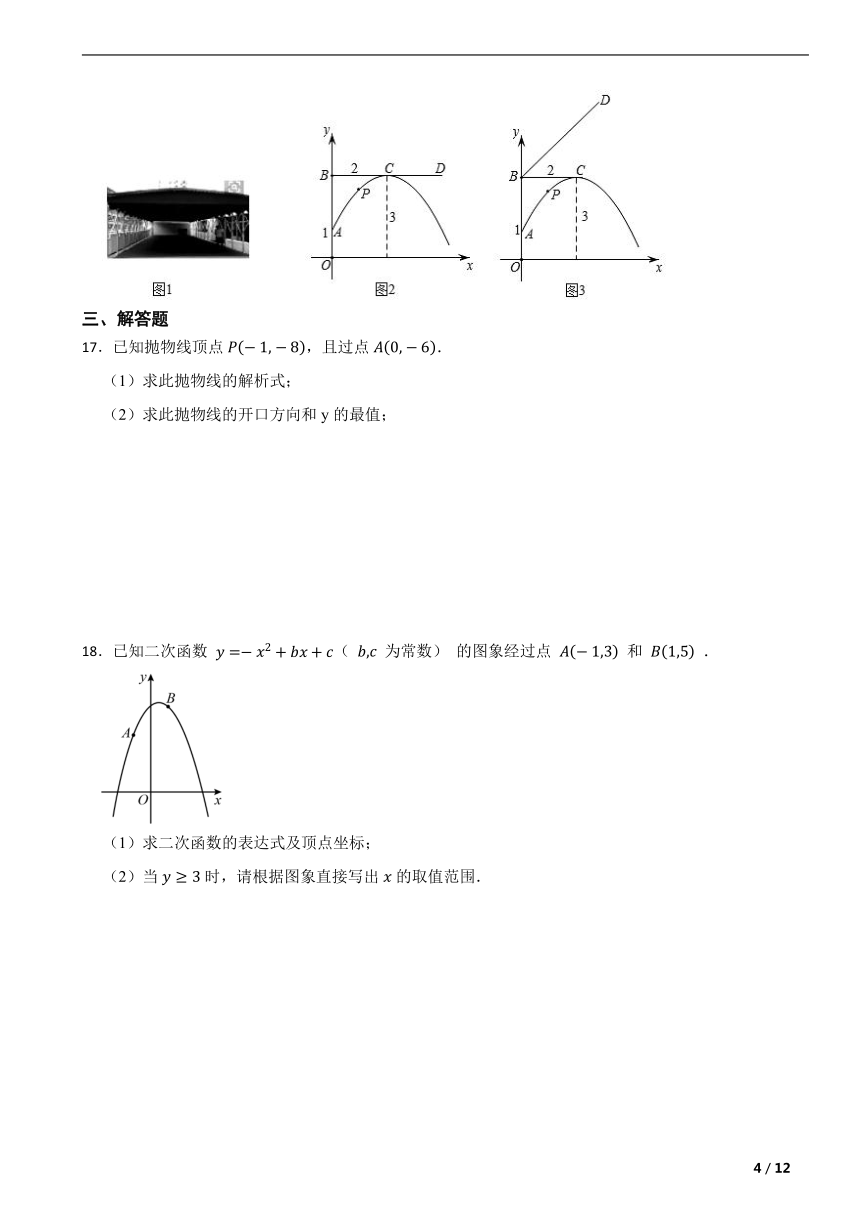
16.准备在一个“7”字型遮阳棚下安装一个喷水装置(如图1),已知遮阳棚DB与竖杆OB垂直,遮阳棚的高度OB=3米,喷水点A与地面的距离OA=1米(喷水点A喷出来的水柱呈抛物线型),水柱喷水的最高点恰好是遮阳棚的C处,C到竖杆的水平距离BC=2米(如图2),此时水柱的函数表达式为 ,现将遮阳棚BD绕点B向上旋转45°(如图3),则此时水柱与遮阳棚的最小距离为 米.(保留根号)
三、解答题
17.已知抛物线顶点,且过点.
(1)求此抛物线的解析式;
(2)求此抛物线的开口方向和y的最值;
18.已知二次函数 ( 为常数) 的图象经过点 和 .
(1)求二次函数的表达式及顶点坐标;
(2)当时,请根据图象直接写出的取值范围.
19.定义:在平面直角坐标系中,横、纵坐标相等的点为“完美点”,顶点是“完美点”的二次函数为“完美函数”.
(1)若点是“完美点”,求的值;
(2)已知某“完美函数”的顶点在直线上,且与轴的交点到原点的距离为,求该“完美函数”的解析式.
20.已知二次函数(其中,为常数).
(1)若函数图象的对称轴为直线,且经过点,求二次函数表达式;
(2)若该二次函数图象经过点,求的值;
(3)在(1)的条件下,若二次函数的图象上有两点,,对于,,总有,求的取值范围.
21.在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数).
(1)求函数图象的对称轴;
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点;
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
22.根据以下素材,探索完成任务.
如何确定防守方案?
素材1 鹰眼系统能够追踪、记录和预测球的轨迹,如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),足球的飞行轨迹可看成抛物线.攻球员位于,守门员位于点,的延长线与球门线交于点,且点,均在足球轨迹正下方,已知,.
素材2 通过鹰眼系统监测,足球飞行的水平速度为水平距离(水平距离=水平速度×时间)与离地高度的鹰眼数据如右表. 守门员的最大防守高度为.守门员在攻球员射门瞬间就作出防守反应,当守门员位于足球正下方时,足球离地高度不大于守门员的最大防守高度视为防守成功. …912151821……5…
问题解决
任务1 确定运动轨迹 求关于的函数表达式.
任务2 探究防守方案 若守门员选择原地接球,能否防守成功?若成功,请求出守门员接住球时,球的高度;若不成功,请通过计算说明理由.
任务3 拟定执行计划 求守门员选择面对足球后退,计算成功防守的最小速度.
23.抛物线与x轴分别交于,两点(点在点的左侧),与轴交于点,抛物线对称轴为,点是第一象限抛物线上动点,连接,.
(1)求抛物线和直线的解析式;
(2)如图1,连接,交于点,设的面积为,的面积为,求的最小值及此时点的坐标;
(3)如图2,设,在直线上方的抛物线上是否存在点,使得恰好等于,若存在,求出点的横坐标;若不存在,请说明理由.
参考答案
1.C
2.B
3.A
4.D
5.B
6.C
7.D
8.C
9.C
10.C
11.
12.
13.
14.16
15.
解:∵二次函数(m为常数)的图象与轴有交点,
∴.
解得:;
∵抛物线的对称轴为直线,抛物线开口向上,且当时,随的增大而增大,
∴,
∴m的取值范围是.
16.;
解:将线段BD沿y轴向下平移,使平移后的线段MN恰好与抛物线只有一个交点,
过点B作BG⊥MN于G,如图:
∵抛物线的顶点C的坐标为,
∴设抛物线的解析式为,
把点的坐标代入得:,
解得:,
∴,
∵,BC⊥y轴,
∴BD与直线平行,且BD与y轴的夹角是45°,
∵,
∴MN与直线平行,,
∴设MN的解析式为,
∵MN与抛物线只有一个交点,
∴方程组只有一组解,
∴方程有两个相等的实数根,
将方程整理得:,
∴,
解得:,
∴MN的解析式为,
令,得,
∴,
∵,
∴(米),
在中,,,
∵,
∴(米),
∴此时水住与遮阳棚的最小距离为米.
17.(1)
(2)开口向上,
18.(1),顶点坐标 为
(2)
19.(1)
(2)或
20.(1)解:∵函数图象的对称轴为直线,且经过点,
∴,解得:,
∴;
(2)解:把代入,得:,
∴,
∴,
∴或;
(3)解:∵,对称轴为直线,
∴抛物线上的点离对称轴越远,函数值越大,
∵对于,,总有,
∴,
∴.
21.(1)解:∵函数y=m(x+1)2+4n(m≠0,且m,n为实数),
∴函数图象的对称轴为x=-1;
(2)证明:令y=0,则0=m(x+1)2+4n,
即,
∵m,n异号,
∴,
∴一元二次方程有两个不相等的实数根,即函数y的图象与x轴有两个不同的交点;
(3)证明:由题可知p=m+4n,q=16m+4n,r=25m+4n,
∵2q-(p+r)=2(16m+4n)-(m+4n+25m+4n)=6m<0,
∴m<0.
22.任务一:
解:任务1:由表格中的数据可知当和当时,h的值相同,
∴该抛物线的对称轴为直线,
∴该抛物线的顶点坐标为,
设该抛物线解析式为,
把代入中得:,
解得,
∴h关于s的函数表达式为;
任务二:
任务2:若守门员选择原地接球,不能防守成功,理由如下:
在中,当时,,
∵,
∴若守门员选择原地接球,不能防守成功;
任务三
:当守门员刚好接到球时,则,
把代入中得:,
解得,
∴此时球的飞行时间为,
∴守门员选择面对足球后退,能够防守成功,那么运动员在内肯定要到达能够刚好接球的位置,即守门员在内的路程要大于等于,
∴守门员的速度要大于等于,
∴守门员的最小速度为.
23.(1)抛物线解析式为,直线的解析式为;
(2)的最小值为,此时
(3)存在,点的横坐标为
1 / 1
一、选择题
1.下列函数属于二次函数的是( ).
A. B.
C. D.
2.二次函数的图象的顶点坐标是( )
A. B. C. D.
3.抛物线先向左平移2个单位长度,再向下平移5个单位长度得到的抛物线的表达式是( )
A. B. C. D.
4.若抛物线经过点,则下列各点,必在抛物线上的是( )
A. B. C. D.
5.二次函数的图象如图所示,反比例函数与正比例函数在同一坐标系内的大致图象是( )
A. B.
C. D.
6.已知二次函数的图象如图所示,该抛物线的对称轴为直线,则下列结论不正确的是( )
A.
B.关于x的方程的两根是
C.当时,y随x的增大而减小
D.
7.已知二次函数y=x2-4x+2,在-1≤x≤3的取值范围内,下列关于该函数的说法中正确的是( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
8.已知点、的坐标分别为、,抛物线的顶点在线段上,抛物线与轴交于、两点(在的左侧),若四边形为平行四边形,则的值为( )
A. B. C. D.
9.如图,正的边长为4,点P为边上的任意一点(不与点B、C重合),且,交于点D.设,,则y关于x的函数图象大致是( )
A. B.
C. D.
10.如图,和都是等腰直角三角形,,,,点A,C,E共线,点F和点G分别是和的中点,,连接,下列结论错误的是( )
A.的最小值是2 B.的最大值为1
C.的最小值为 D.的最小值为
二、填空题
11.当 时,函数是二次函数.
12.把二次函数,化成的形式是 .
13.已知,在二次函数的图象上,比较 .(填、或)
14.如图,将抛物线沿y轴向下平移一段距离后,得到一条新的抛物线;若曲线段平移至曲线段,曲线段所扫过的为阴影部分,则阴影部分的面积是 .
15.已知二次函数(为常数)的图象与轴有交点,且当时,随的增大而增大,则的取值范围是 .
16.准备在一个“7”字型遮阳棚下安装一个喷水装置(如图1),已知遮阳棚DB与竖杆OB垂直,遮阳棚的高度OB=3米,喷水点A与地面的距离OA=1米(喷水点A喷出来的水柱呈抛物线型),水柱喷水的最高点恰好是遮阳棚的C处,C到竖杆的水平距离BC=2米(如图2),此时水柱的函数表达式为 ,现将遮阳棚BD绕点B向上旋转45°(如图3),则此时水柱与遮阳棚的最小距离为 米.(保留根号)
三、解答题
17.已知抛物线顶点,且过点.
(1)求此抛物线的解析式;
(2)求此抛物线的开口方向和y的最值;
18.已知二次函数 ( 为常数) 的图象经过点 和 .
(1)求二次函数的表达式及顶点坐标;
(2)当时,请根据图象直接写出的取值范围.
19.定义:在平面直角坐标系中,横、纵坐标相等的点为“完美点”,顶点是“完美点”的二次函数为“完美函数”.
(1)若点是“完美点”,求的值;
(2)已知某“完美函数”的顶点在直线上,且与轴的交点到原点的距离为,求该“完美函数”的解析式.
20.已知二次函数(其中,为常数).
(1)若函数图象的对称轴为直线,且经过点,求二次函数表达式;
(2)若该二次函数图象经过点,求的值;
(3)在(1)的条件下,若二次函数的图象上有两点,,对于,,总有,求的取值范围.
21.在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数).
(1)求函数图象的对称轴;
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点;
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
22.根据以下素材,探索完成任务.
如何确定防守方案?
素材1 鹰眼系统能够追踪、记录和预测球的轨迹,如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),足球的飞行轨迹可看成抛物线.攻球员位于,守门员位于点,的延长线与球门线交于点,且点,均在足球轨迹正下方,已知,.
素材2 通过鹰眼系统监测,足球飞行的水平速度为水平距离(水平距离=水平速度×时间)与离地高度的鹰眼数据如右表. 守门员的最大防守高度为.守门员在攻球员射门瞬间就作出防守反应,当守门员位于足球正下方时,足球离地高度不大于守门员的最大防守高度视为防守成功. …912151821……5…
问题解决
任务1 确定运动轨迹 求关于的函数表达式.
任务2 探究防守方案 若守门员选择原地接球,能否防守成功?若成功,请求出守门员接住球时,球的高度;若不成功,请通过计算说明理由.
任务3 拟定执行计划 求守门员选择面对足球后退,计算成功防守的最小速度.
23.抛物线与x轴分别交于,两点(点在点的左侧),与轴交于点,抛物线对称轴为,点是第一象限抛物线上动点,连接,.
(1)求抛物线和直线的解析式;
(2)如图1,连接,交于点,设的面积为,的面积为,求的最小值及此时点的坐标;
(3)如图2,设,在直线上方的抛物线上是否存在点,使得恰好等于,若存在,求出点的横坐标;若不存在,请说明理由.
参考答案
1.C
2.B
3.A
4.D
5.B
6.C
7.D
8.C
9.C
10.C
11.
12.
13.
14.16
15.
解:∵二次函数(m为常数)的图象与轴有交点,
∴.
解得:;
∵抛物线的对称轴为直线,抛物线开口向上,且当时,随的增大而增大,
∴,
∴m的取值范围是.
16.;
解:将线段BD沿y轴向下平移,使平移后的线段MN恰好与抛物线只有一个交点,
过点B作BG⊥MN于G,如图:
∵抛物线的顶点C的坐标为,
∴设抛物线的解析式为,
把点的坐标代入得:,
解得:,
∴,
∵,BC⊥y轴,
∴BD与直线平行,且BD与y轴的夹角是45°,
∵,
∴MN与直线平行,,
∴设MN的解析式为,
∵MN与抛物线只有一个交点,
∴方程组只有一组解,
∴方程有两个相等的实数根,
将方程整理得:,
∴,
解得:,
∴MN的解析式为,
令,得,
∴,
∵,
∴(米),
在中,,,
∵,
∴(米),
∴此时水住与遮阳棚的最小距离为米.
17.(1)
(2)开口向上,
18.(1),顶点坐标 为
(2)
19.(1)
(2)或
20.(1)解:∵函数图象的对称轴为直线,且经过点,
∴,解得:,
∴;
(2)解:把代入,得:,
∴,
∴,
∴或;
(3)解:∵,对称轴为直线,
∴抛物线上的点离对称轴越远,函数值越大,
∵对于,,总有,
∴,
∴.
21.(1)解:∵函数y=m(x+1)2+4n(m≠0,且m,n为实数),
∴函数图象的对称轴为x=-1;
(2)证明:令y=0,则0=m(x+1)2+4n,
即,
∵m,n异号,
∴,
∴一元二次方程有两个不相等的实数根,即函数y的图象与x轴有两个不同的交点;
(3)证明:由题可知p=m+4n,q=16m+4n,r=25m+4n,
∵2q-(p+r)=2(16m+4n)-(m+4n+25m+4n)=6m<0,
∴m<0.
22.任务一:
解:任务1:由表格中的数据可知当和当时,h的值相同,
∴该抛物线的对称轴为直线,
∴该抛物线的顶点坐标为,
设该抛物线解析式为,
把代入中得:,
解得,
∴h关于s的函数表达式为;
任务二:
任务2:若守门员选择原地接球,不能防守成功,理由如下:
在中,当时,,
∵,
∴若守门员选择原地接球,不能防守成功;
任务三
:当守门员刚好接到球时,则,
把代入中得:,
解得,
∴此时球的飞行时间为,
∴守门员选择面对足球后退,能够防守成功,那么运动员在内肯定要到达能够刚好接球的位置,即守门员在内的路程要大于等于,
∴守门员的速度要大于等于,
∴守门员的最小速度为.
23.(1)抛物线解析式为,直线的解析式为;
(2)的最小值为,此时
(3)存在,点的横坐标为
1 / 1
同课章节目录
