浙江省2025年中考数学三轮冲刺【最新中考模拟题】专项练习 09 填空题 (含答案+解析)
文档属性
| 名称 | 浙江省2025年中考数学三轮冲刺【最新中考模拟题】专项练习 09 填空题 (含答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 704.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 09:18:07 | ||
图片预览



文档简介
浙江省2025年中考数学三轮冲刺【最新中考模拟题】
专项练习 09 填空题
一、填空题
1.(2025·杭州模拟) 已知二次函数与一次函数(a是常数)的图象交于两个不同的点A,B,若点A的横坐标是-1,则点B的横坐标是 .
2.(2025·浙江模拟)因式分解:x2-4=
3.(2025·宁海模拟)因式分解: = .
4.(2025·西湖模拟)已知二次函数与一次函数(是常数)的图象交于两个不同的点,若点的横坐标是,则点的横坐标是 .
5.(2025·普陀二模)已知点(m,n)在直线y=x+b(b为常数)上,若mn的最小值为-1,则b= 。
6.(2025·浙江模拟)因式分解:x2+2x=
7.(2025·普陀二模)若二次根式 有意义,则x的取值范围是 .
8.(2025·乐清二模)不等式组的解集为 。
9.(2025·玉环二模)因式分解: .
10.(2025·文成二模)如图,在中,是BC边上的中线,将沿AD翻折至,点落在点处,连结CE,BE.记四边形ADEC面积为的面积为,则的值是 .
11.(2025·文成二模)有3张卡片,上面分别写着0,1,2,从中随机抽取2张,数字之积为0的概率是 .
12.(2025·婺城模拟)如图,在矩形ABCD中,,将矩形ABCD绕点顺时针旋转,旋转得矩形,继续旋转使得点的对应点落在上,连结,则 .
13.(2025·椒江二模) 已知直角坐标系内有四个点O(0,0),A(1,1),B(3,1),C(x,0),若以O,A,B,C为顶点的四边形是平行四边形,则x= .
14.(2025·长兴模拟)如图,在平面直角坐标系中,已知点,以原点为位似中心,作的位似图形,并把的边长缩小到原来的,则点的对应点的坐标是 .
15.(2025·龙港模拟)如图,是的直径,,D是的中点,.若,则的长为 .
16.(2025·玉环二模)若分式有意义,则的取值范围是 .
17.(2025·玉环二模)分解因式: .
18.(2025·温岭二模)在矩形ABCD中,为BC的中点,将沿着AE翻折,得到,连接DG并延长与AE相交于点,与AB相交于点.若点恰好为AE的中点,则的值为 .
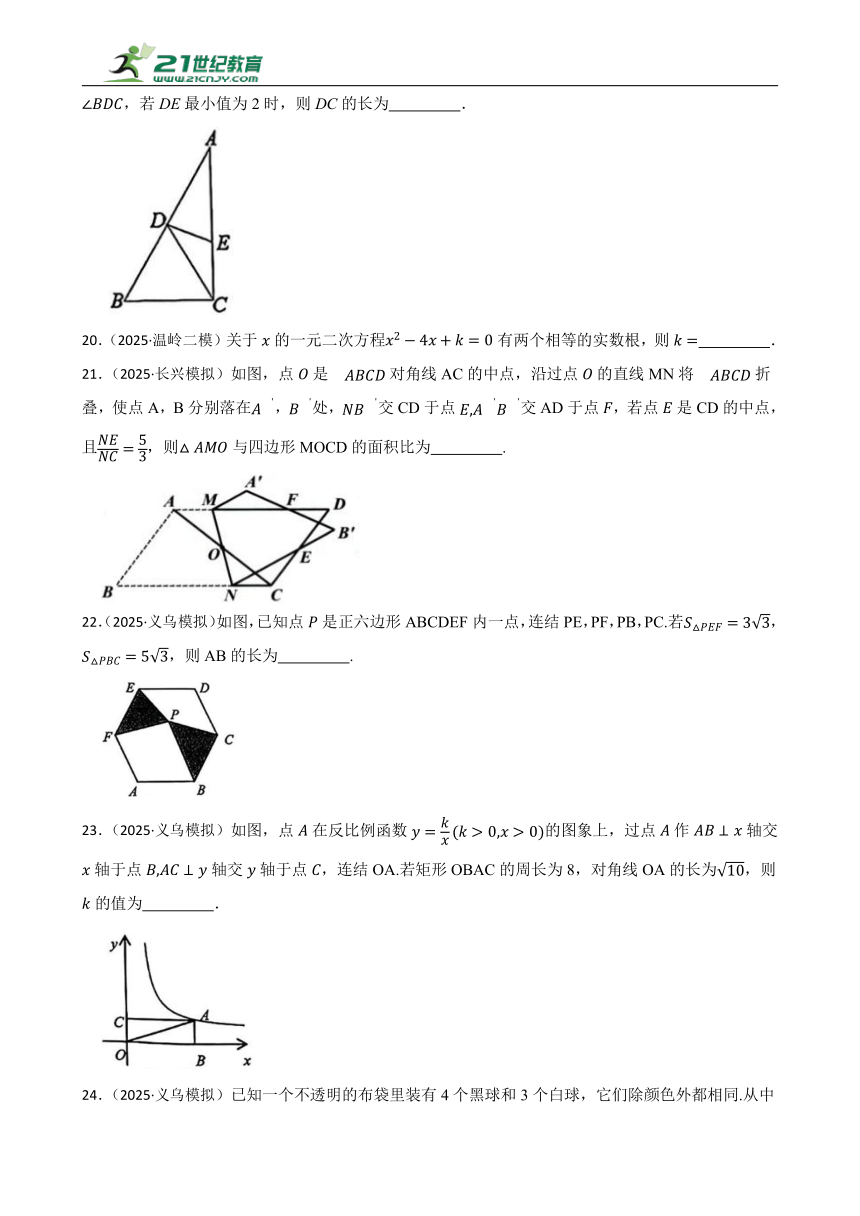
19.(2025·温岭二模)如图,在中,CD为AB边上的中线,为AC上任意一点,,若DE最小值为2时,则DC的长为 .
20.(2025·温岭二模)关于的一元二次方程有两个相等的实数根,则 .
21.(2025·长兴模拟)如图,点是对角线AC的中点,沿过点的直线MN将折叠,使点A,B分别落在,处,交CD于点交AD于点,若点是CD的中点,且,则与四边形MOCD的面积比为 .
22.(2025·义乌模拟)如图,已知点是正六边形ABCDEF内一点,连结PE,PF,PB,PC.若,,则AB的长为 .
23.(2025·义乌模拟)如图,点在反比例函数的图象上,过点作轴交轴于点轴交轴于点,连结OA.若矩形OBAC的周长为8,对角线OA的长为,则的值为 .
24.(2025·义乌模拟)已知一个不透明的布袋里装有4个黑球和3个白球,它们除颜色外都相同.从中任意摸出一个球,恰好摸到黑球的概率是 .
25.(2025·婺城模拟)如图,在半径为4的扇形AOB中,,点为OB中点,作交OA于点,则围成的图形(阴影部分)的周长为 .
26.(2025·椒江二模)一个不透明的布袋中有2个红球和1个白球,它们除颜色外其他都相同,若从布袋里随机摸出1个球,则摸到白球的概率为 .
27.(2025·龙港模拟)新定义:我们把抛物线,(其中)与抛物线称为“孪生抛物线”,例如:抛物线的“孪生抛物线”为.已知抛物线(a为常数,且)的“孪生抛物线”为.抛物线的顶点为A,与x轴交于B,C两点,若为直角三角形,则抛物线的表达式为 .
28.(2025·萧山模拟)已知点A是正比例函数图象上一点,把点A向上平移4个单位,向右平移个单位后的点仍在这个正比例函数的图象上,则 .
29.(2025·萧山模拟)如图,等腰内接于,,将折叠至,使点D落在上.若过点O,则 .
30.(2025·萧山模拟)如图,,平分,若,则 .
31.(2025·萧山模拟)计算: .
32.(2025·南山模拟)因式分解: .
33.(2025·龙港模拟)因式分解: = .
34.(2025·钱塘模拟)如图,内接于,,交于点,连结.若,则的大小为 .
35.(2025·鹿城模拟)如图,在菱形ABCD中,是对角线AC上一点,连接BE,将绕着点旋转,点的对应点落在边AD上,点的对应点落在边AB上,BF与AC交于点.若是AD的中点,则HE的长为 .
36.(2025·鹿城模拟)若扇形的圆心角为,半径为2,则它的面积为 .
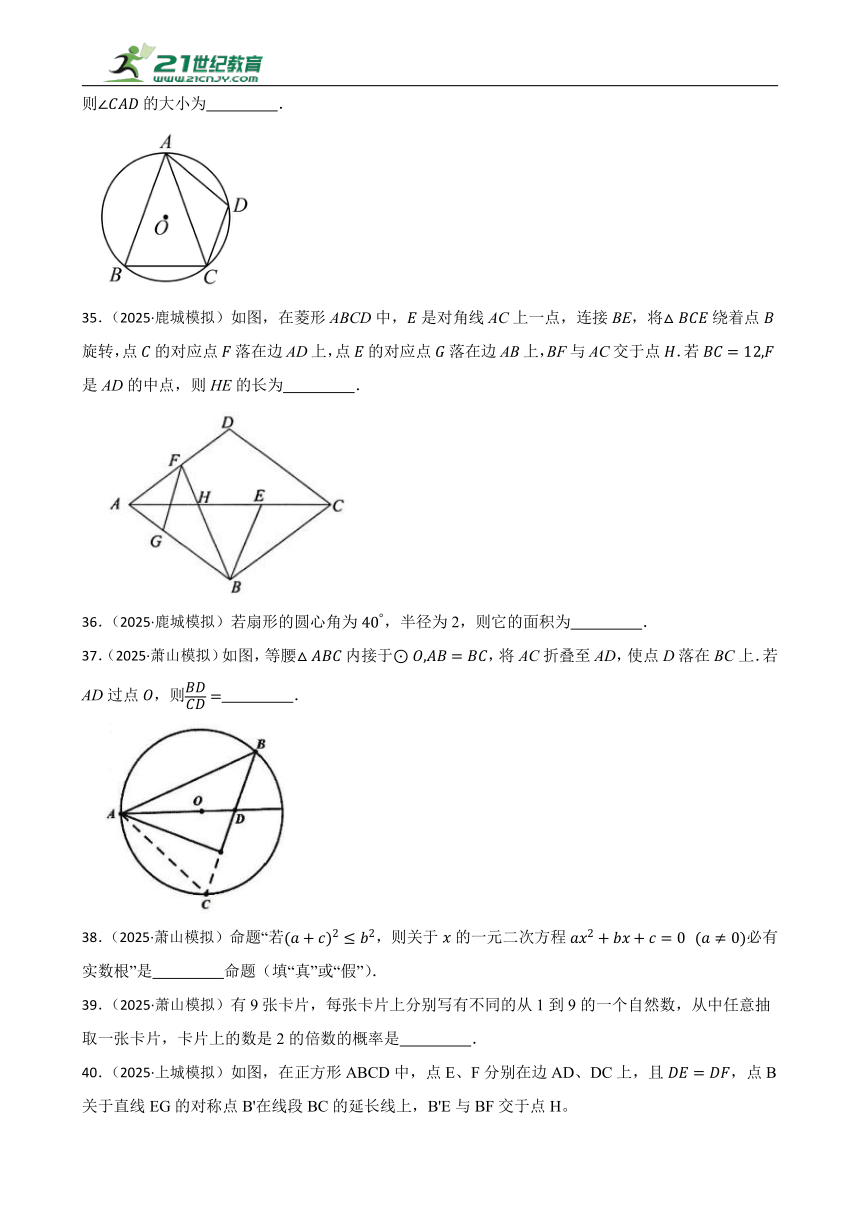
37.(2025·萧山模拟)如图,等腰内接于,将AC折叠至AD,使点D落在BC上.若AD过点,则 .
38.(2025·萧山模拟)命题“若,则关于的一元二次方程必有实数根”是 命题(填“真”或“假”).
39.(2025·萧山模拟)有9张卡片,每张卡片上分别写有不同的从1到9的一个自然数,从中任意抽取一张卡片,卡片上的数是2的倍数的概率是 .
40.(2025·上城模拟)如图,在正方形ABCD中,点E、F分别在边AD、DC上,且,点B关于直线EG的对称点B'在线段BC的延长线上,B'E与BF交于点H。
(1)若点A与点H关于直线BE对称,则 ;
(2)若,则 。
41.(2025·上城模拟)把电阻值分别为,的两电阻并联后接入某电路中,其并联总电阻值R(单位:Ω)满足。当时, 。
42.(2025·定海模拟)若圆锥的底面半径是1,它的侧面展开图的圆心角是直角,则该圆锥的高为 .
43.(2025·定海模拟)哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是 .
44.(2025·杭州模拟) 如图是一张菱形纸片ABCD,点E在AD边上,,把沿直线CE折叠得到,点D'落在DA的延长线上. 若CD'恰好平分,则 °, .
45.(2025·杭州模拟) 如图,的切线PA与直径CB的延长线交于点A,点P为切点,连接PC若 , 则的度数为 °.
46.(2025·西湖模拟)如图是一张菱形纸片,点在边上,,把沿直线折叠得到,点落在的延长线上.若恰好平分,则 °, .
47.(2025·拱墅模拟) 在图中,中,, BD是的角平分线,点在BD上,过点E作,交AB于点.若,,,则 .
48.(2025·拱墅模拟) 若一次函数 的图象过点 ,,其中 ,则 .
49.(2025·临安模拟)如图,是边长为6的等边三角形,点为延长线上一点,,过作所在直线的垂线,垂足为,连结,为中点,则线段的长是 .
50.(2025·温州模拟)某挂饰由圆盘和挂绳组成(如图),AB,AC分别切⊙O于点B,C.若∠A=64°,则的度数为 度.
答案解析部分
1.3
解:∵二次函数 与一次函数 (a是常数)的图象交于两个不同的点A,B,点A的横坐标是
∴二次函数为 一次函数为 令
解得 或
∴点B的横坐标是3.
故答案为:3.
由题意得到 求得 则二次函数为 一次函数为 令 解方程即可求得点B的横坐标.
2.(x+2)(x-2)
解:x2-4=(x+2)(x-2).
故答案为:(x+2)(x-2).
直接利用平方差公式法分解即可。
3.(a-2)(a+2)
原式=(a-2)(a+2).
故答案为(a-2)(a+2).
直接利用平方差公式分解即可.
4.
5.±2
6.x(x+2)
解:原式=x(x+2),
故答案为:x(x+2).
直接利用提公因式法分解即可。
7.x≥2
解:根据题意,使二次根式 有意义,即x﹣2≥0,
解得x≥2;
故答案为:x≥2.
根据二次根式有意义的条件,可得x﹣2≥0,解不等式求范围.
8.
解:
解第一个不等式得:x>-1,
解第二个不等式得:x≤6.
则不等式组的解集是:-1<x≤6,
故答案为:-1<x≤6.
两个不等式的解集的公共部分就是不等式组的解集.
9.
解:m2+m=m(m+1),
故答案为:m(m+1).
由于第一项和第二项相同字母m的最低次方为1,提取公因式m即可。
10.
解:如图,延长AD交BE于点F,
∵AC∶BC=3∶4,
∴设AC=3x,BC=4x,
在Rt△ABC中,AB=,
∵点D是BC的中点,
∴BD=CD=2x,
在Rt△ACD中,AD=;
由翻折得AE=AB=5x,DE=BD=CD=2x,
∴AD是BE的垂直平分线,∠DBE=∠DEB,∠DEC=∠DCE,
∵∠DBE+∠DEB+∠DEC+∠DCE=2(∠BED+∠DEC)=180°,
∴∠BEC=∠BED+∠CED=90°,
∴△BCE是直角三角形,
设DF=y,则AF=AD+DF=,
由勾股定理得AF2=AE2-EF2,EF2=DE2-DF2,
∴AF2=AE2-DE2+DF2,即,
解得,即DF=,
∵∠AFB=∠CEB=90°,
∴DF∥CE,
∴△BDF∽△BCE,
∴,即,
∴
∴,
∵S△ABC=,S△BCE=,
∵点D是BC的中点,
∴S△ACD=S△ABD=,S△CED=,
∴S1=S△ACD+S△CDE=,S2=S△ABD=3x2,
∴.
故答案为:.
延长AD交BE于F,设AC=3x,BC=4x,由勾股定理得AB=5x,AD=;由翻折得AE=AB=5x,DE=BD=CD=2x,根据“到线段两端点的距离相等的点在这条线段的垂直平分线上及两点确定一条直线”得AD是BE的垂直平分线,由等边对等角及三角形的内角定理可推出△BCE是直角三角形,设DF=y,则AF=AD+DF=,由勾股定理可得AF2=AE2-DE2+DF2,据此建立方程求出,即DF=,由同位角相等两直线平行,得DF∥CE,由平行于三角形一边得直线截其它两边,所截三角形与原三角形相似得△BDF∽△BCE,由相似三角形对应边成比例建立方程可得,根据勾股定理表示出BE,然后根据三角形面积计算公式分别计算出△ABC、△BCE的面积,由等底同高三角形面积相等得出△ACD、△ABD、△CED的面积,进而根据S1=S△ACD+S△CDE算出S1,最后再求出两个面积之比即可.
11.
解:从3张分别写着 0,1,2,的卡片中随机的抽取两张,共有0、1,0、2,1、2,三种,其中乘积为0的有0、1与0、2两种,∴ 从中随机抽取2张,数字之积为0的概率是.
故答案为:.
利用列举法列举出从3张分别写着 0,1,2,的卡片中随机的抽取两张的所有情况,再根据有理数乘法法则“任何数与0相乘都等于0”找出其中乘积为0的情况数,从而根据概率公式计算可得答案.
12.
解:由题意可得:BC=AD,∠BAD=90°,
∵将矩形ABCD绕点A顺时针旋转,旋转90°得矩形A1B1C1D1,继续旋转使得点B的对应点B2落在B1D1上,
∴AB=AB1=AB2,∠B1AD1=90°,AD1=AD,
∴点B、B1、B2在以点A为圆心,AB为半径的圆上,
∴,
∵AB=AB1=AB2,
∴,
∠ABB2=∠AB2A,
∵∠B1AD1+∠BAD=180°,
∴B、A、D1在同一直线上,
∵∠B2BD1+∠B2D1B=∠B1B2B=45°,
∠B1BB2+∠B2BA=∠B2BA=45°,
∴∠B1BB2=∠B2D1B,
∵AB:BC=3:4,
∴设AB1=AB=3x,则AD=AD1=BC=4x,
∴,
∴,
故答案为:.
根据矩形的性质得出BC=AD,∠BAD=90°,根据旋转的性质得出AB=AB1=AB2,∠B1AD1= 90°,AD1=AD,证明点B、B1、B2在以点A为圆心,AB为半径的圆上,根据圆周角定理得出,证明,设AB1=AB=3x,则AD=AD1=BC=4x,根据勾股定理得出,根据三角函数定义即可求出答案.
13.2或-2
14.
15.
16.
解:要使分式有意义,则x+1≠0,因此x≠-1
故答案为:x≠-1.
本题考查的是分式有意义的条件:分母不为0即可.
17.
解:
=
故答案为:.
先提取公因式-1,把二次项系数化为正,再利用完全平方公式因式分解即可.
18.
19.4
20.4
21.
22.4
解:∵多边形ABCDEF是正六边形,设AB的长为a,
∴正六边形的面积为,
∵,,
∴,
∴a=4,
则AB的长为4.
故答案为:4.
先求出正六边形的面积,再根据、的占比即可求解.
23.3
解:设点A的坐标为,根据题意:
∵矩形OBAC的周长为8,得:,
∴
对角线OA的长度为,得:
将平方得:
结合,代入得:
10+2k=16
∴k=3
故答案为:3.
利用反比例函数解析式,设点A坐标为,根据矩形周长公式和勾股定理,建立关于a和k的方程组,通过代数变形(如平方展开)消元,最终求出k的值.
24.
解:∵一个口袋里装有4个黑球,3个白球
∴从中任意摸出一个球,摸到黑球的概率为:
故答案为:.
用黑球的个数除以球的总个数即可求得摸到黑球的概率.
25.
解:由条件可知OA=OB=4,
∵∠AOB=45°
∴
∵点P为OB中点,
∴,
由条件可得△OPQ为等腰直角三角形,
∴QP=OP=2,
∴,
∴,
∴阴影部分的周长
故答案为:.
利用弧长公式可得,又由△OPQ为等腰直角三角形可得,即得,进而求出周长即可.
26.
27.
28.2
29.
30.
31.
32.(x-4)2
解:x2-8x+16=(x-4)2.
故答案为:(x-4)2.
直接利用完全平方公式进行分解即可.
33.
解: .
直接应用平方差公式即可求解. .
34.
35.
解:∵△BCE旋转得到△BFG,
∴△BCE △BFG,
∴BC=BF,∠ABH=∠CBE
∵ABCD是菱形,BC=12,
∴AD=BC=AB=CD=12,AD//BC
∴∠DAC=∠BCH,∠AFH=∠CBH,
∴△AFH∽△CBH
∵F是AD的中点,
∴
∴,
∵AB=BC,
∴∠BAC=∠BCA,
在△ABH和△CBE中,
∴△ABH≌△CBE(ASA),
∴BH=BE=8,AH=EC,
∵
∴AH=HE=EC,
过B作BK⊥HE交于点K,
∵BH=BE=8,HE=EC
由等腰三角形三线合一可得HK=KE,
设HK=KE=x,EC=HE=2x,
在Rt△BKE和Rt△BKC中,由勾股定理可得:
BK2=BE2-KE2=BC2-KC2
∴82-x2=122-(x+2x)2,
解得(舍去)或,
∴,
故答案为:.
证明△AFH∽△CBH和△ABH≌△CBE(ASA),并根据等腰三角形三线合一得出HK=KE,进一步在Rt△BKE和Rt△BKC中,由勾股定理可得:BK2=BE2-KE2=BC2-KC2建立方程求解即可得出HE的长.
36.
解:由题意可得,
故答案为:.
利用扇形的面积公式进行计算即可.
37.
解:
如图,过D作DP⊥AB于P
设∠MAC=x,∠C=y
由折叠知,∠MAC=∠DAM=x,∠AMC=90°,DM=MC
∴x+y=90°
∵AN为直径
∴∠ABN=90°
在圆中,∠C=∠N=y
∴∠ABN=90°-y=x
∴∠BAC=3x
∵AB=BC
∴∠BAC=∠BCA
∴3x=y
∴x+y=4x=90°
故x=22.5°
∴∠BAM=45°,
∴△AMB为等腰直角三角形,△DPB也为等腰直角三角形
∵∠BAD=∠MAD,DP⊥AB,DM⊥AM
∴PD=DM
∴
∴
故答案为:.
通过设∠MAC=x,∠C=y,根据折叠知∠AMC=90°,得x+y=90°,利用圆的性质和同角余角相等,进一步求得3x=y,从而求得x=22.5°,因此△BPD为等腰直角三角形,最后利用边的比例关系求解.
38.真
解:
∵(a+c)2b2,
∴a2+2ac+c2≤b2,
∴a2-2ac+c2≤b2-4ac,
∵(a-c)2≤b2-4ac,(a-c)2≥0
∴b2-4ac≥0,
∴关于x的一元二次方程ax2+bx+c=0(a≠0)必有实数根,
∴命题“若(a+c)2≤b2,则关于x的一元二次方程ax2+bx+c=0(a≠0)必有实数根”是真命题,
故答案为:真.
题目通过条件 ( a+c )2 ≤b2推导出判别式△ ≥ (a c)2≥0,从而得出方程必有实根的结论.
39.
解:
∵1~9中2的倍数有2、4、6、8四个数,
∴抽到的卡片上的数是2的倍数的概率是
故答案为:.
先得出2的倍数,再根据概率公式即可得出结论.
40.(1)
(2)
解:(1)∵ 点B关于直线EG的对称点B'在线段BC的延长线上,
∴EB=EB',
∴∠EBB'=∠EB'B,
又∵ABCD是正方形,
∴AD∥BC,∠ABC=90°,
∴∠AEB=∠EBC,
由折叠可得∠AEB=∠B'EB,
∴∠EBB'=∠EB'B=∠BEB'=60°,
∴∠ABE=30°,
∴;
(2)如图,过点B'作B'N∥CD,过点F作FM∥BC交B'E、B'N于点M、N两点,设FM=a,DE=DF=x,则四边形CB'NF为矩形,
∴FN=CB',B'N=CF,
∵B'N∥CD,
∴△HFM∽△HBB',
∴,即,
∵点B关于直线EG的对称点B'在线段BC的延长线上,
∴BG=B'G=6a,EG⊥BC,
∴CD=BC=EG=AB=AD=AE+ED=BG+DE=6a+x,
又∵DF=DE=x,
∴B'N=CF=6a,
又又问我FN=CB'=GB'-CB'=6a-x,
∴MN=FM+FN=a+6a-x=7a-x,
又∵FM∥BC,
∴∠NMB'=∠MB'G,
又∵∠N=∠EGB'=90°,
∴△B'NM∽△EGB',
∴,即,
解得x=3a或x=-2a,
∴;
故答案为:;.
(1)根据正方形的性质和轴对称可得∠EBB'=∠EB'B=∠BEB'=60°,即可求出∠ABE=30°,进而计算正切即可;
(2)过点B'作B'N∥CD,过点F作FM∥BC交B'E、B'N于点M、N两点,设FM=a,DE=DF=x,则四边形CB'NF为矩形,先根据△HFM∽△HBB',求出BB'的长,然后证明△B'NM∽△EGB',利用对应边成比例求出x=3a,然后代入计算比值即可.
41.
解:∵ ,
∴,
∴,
故答案为:.
把 代入计算可得,然后求出比值即可解题.
42.
解:设圆锥的母线长为l,
∵圆锥的底面圆半径为1,
∴圆锥侧面展开图扇形的弧长为,
∵圆锥的侧面展开图的圆心角是直角,
∴,
解得:l=4,
∴圆锥的高为:,
故答案为:.
设圆锥的母线长为l,根据圆锥的侧面展开图扇形的弧长等于圆锥底面圆周长,结合弧长公式得,从而求出l=4,进而利用勾股定理即可求解.
43.
解:列表如下:
2 3 5
2 5 7
3 5 8
5 7 8
∴共有6种等可能结果,其中和是偶数的有2种,
∴随机选取两个不同的数,其和是偶数的概率是,
故答案为:.
利用列表法得出所有的等可能结果数,从而得其中和是偶数的结果数,进而利用概率公式进行计算即可.
44.36;
解:设AB, 交于点J.设∠B=x.
∵四边形ABCD是菱形,
∴∠B=∠D =x,AD∥CB,
∴∠BCD'=∠D',
∵CD'平分∠ACB,
∴∠ACD'=∠BCD',
由翻折变换的性质可知,∠D =∠D',
∴∠BCD'=∠ACD'=x,
∵BA=BC,
∴∠BCA=∠BAC=2x,
∵∠B+∠ACB+∠BAC=180°,
∴5x=180°,
设 , 则.
故答案为:36,
设AB, 交于点J.设. .利用三角形内角和定理构建方程求出x即可,证明设,则 利用相似三角形的性质构建一元二次方程求解.
45.35
解:如图, 连接OP,
∵ PA是⊙O的切线,
由圆周角定理得:
故答案为: 35.
连接OP,根据切线的性质得到 根据直角三角形的性质求出. 再根据圆周角定理解答即可.
46.;
47.
解:作DH⊥AB于点H, 则∠BHD =∠C =90°,
∵BD是∠ABC的角平分线,
∴∠HBD=∠CBD,
∵BD=BD,
∴△HBD≌△CBD(AAS)
∵EF⊥BD于点E,
∴∠BEF = 90°,
∵BE=4, BF=5,
∴BD=BE+DE=4+3=7,
故答案为:
作DH⊥AB于点H, 则∠BHD=∠C=90°, 而∠HBD=∠CBD, BD=BD, 可根据“AAS”证明△HBD≌△CBD,根据勾股定理求得DE =EF=3, 则BD=7, 由余弦的定义求出BH长,即可求出BC长解题.
48.-1
解:∵一次函数 的图象过点(1,m), (m,1),
解得:
故答案为:
利用一次函数图象上点的坐标特征,可得出关于k的方程组,解之即可得出结论.
49.
50.116
解:连接圆心O与切点B、C,
根据切线性质,OB⊥AB,OC⊥AC,
∵四边形ABOC内角和为360°,∠A=64°,∠ABO=∠ACO=90°,
∴∠BOC=360°-64°-90-90°=116°,
∴弧BC的度数为116°,
故答案为:116.
根据切线性质可知∠ABO=∠ACO=90°,再根据四边形内角和即可求解.
专项练习 09 填空题
一、填空题
1.(2025·杭州模拟) 已知二次函数与一次函数(a是常数)的图象交于两个不同的点A,B,若点A的横坐标是-1,则点B的横坐标是 .
2.(2025·浙江模拟)因式分解:x2-4=
3.(2025·宁海模拟)因式分解: = .
4.(2025·西湖模拟)已知二次函数与一次函数(是常数)的图象交于两个不同的点,若点的横坐标是,则点的横坐标是 .
5.(2025·普陀二模)已知点(m,n)在直线y=x+b(b为常数)上,若mn的最小值为-1,则b= 。
6.(2025·浙江模拟)因式分解:x2+2x=
7.(2025·普陀二模)若二次根式 有意义,则x的取值范围是 .
8.(2025·乐清二模)不等式组的解集为 。
9.(2025·玉环二模)因式分解: .
10.(2025·文成二模)如图,在中,是BC边上的中线,将沿AD翻折至,点落在点处,连结CE,BE.记四边形ADEC面积为的面积为,则的值是 .
11.(2025·文成二模)有3张卡片,上面分别写着0,1,2,从中随机抽取2张,数字之积为0的概率是 .
12.(2025·婺城模拟)如图,在矩形ABCD中,,将矩形ABCD绕点顺时针旋转,旋转得矩形,继续旋转使得点的对应点落在上,连结,则 .
13.(2025·椒江二模) 已知直角坐标系内有四个点O(0,0),A(1,1),B(3,1),C(x,0),若以O,A,B,C为顶点的四边形是平行四边形,则x= .
14.(2025·长兴模拟)如图,在平面直角坐标系中,已知点,以原点为位似中心,作的位似图形,并把的边长缩小到原来的,则点的对应点的坐标是 .
15.(2025·龙港模拟)如图,是的直径,,D是的中点,.若,则的长为 .
16.(2025·玉环二模)若分式有意义,则的取值范围是 .
17.(2025·玉环二模)分解因式: .
18.(2025·温岭二模)在矩形ABCD中,为BC的中点,将沿着AE翻折,得到,连接DG并延长与AE相交于点,与AB相交于点.若点恰好为AE的中点,则的值为 .
19.(2025·温岭二模)如图,在中,CD为AB边上的中线,为AC上任意一点,,若DE最小值为2时,则DC的长为 .
20.(2025·温岭二模)关于的一元二次方程有两个相等的实数根,则 .
21.(2025·长兴模拟)如图,点是对角线AC的中点,沿过点的直线MN将折叠,使点A,B分别落在,处,交CD于点交AD于点,若点是CD的中点,且,则与四边形MOCD的面积比为 .
22.(2025·义乌模拟)如图,已知点是正六边形ABCDEF内一点,连结PE,PF,PB,PC.若,,则AB的长为 .
23.(2025·义乌模拟)如图,点在反比例函数的图象上,过点作轴交轴于点轴交轴于点,连结OA.若矩形OBAC的周长为8,对角线OA的长为,则的值为 .
24.(2025·义乌模拟)已知一个不透明的布袋里装有4个黑球和3个白球,它们除颜色外都相同.从中任意摸出一个球,恰好摸到黑球的概率是 .
25.(2025·婺城模拟)如图,在半径为4的扇形AOB中,,点为OB中点,作交OA于点,则围成的图形(阴影部分)的周长为 .
26.(2025·椒江二模)一个不透明的布袋中有2个红球和1个白球,它们除颜色外其他都相同,若从布袋里随机摸出1个球,则摸到白球的概率为 .
27.(2025·龙港模拟)新定义:我们把抛物线,(其中)与抛物线称为“孪生抛物线”,例如:抛物线的“孪生抛物线”为.已知抛物线(a为常数,且)的“孪生抛物线”为.抛物线的顶点为A,与x轴交于B,C两点,若为直角三角形,则抛物线的表达式为 .
28.(2025·萧山模拟)已知点A是正比例函数图象上一点,把点A向上平移4个单位,向右平移个单位后的点仍在这个正比例函数的图象上,则 .
29.(2025·萧山模拟)如图,等腰内接于,,将折叠至,使点D落在上.若过点O,则 .
30.(2025·萧山模拟)如图,,平分,若,则 .
31.(2025·萧山模拟)计算: .
32.(2025·南山模拟)因式分解: .
33.(2025·龙港模拟)因式分解: = .
34.(2025·钱塘模拟)如图,内接于,,交于点,连结.若,则的大小为 .
35.(2025·鹿城模拟)如图,在菱形ABCD中,是对角线AC上一点,连接BE,将绕着点旋转,点的对应点落在边AD上,点的对应点落在边AB上,BF与AC交于点.若是AD的中点,则HE的长为 .
36.(2025·鹿城模拟)若扇形的圆心角为,半径为2,则它的面积为 .
37.(2025·萧山模拟)如图,等腰内接于,将AC折叠至AD,使点D落在BC上.若AD过点,则 .
38.(2025·萧山模拟)命题“若,则关于的一元二次方程必有实数根”是 命题(填“真”或“假”).
39.(2025·萧山模拟)有9张卡片,每张卡片上分别写有不同的从1到9的一个自然数,从中任意抽取一张卡片,卡片上的数是2的倍数的概率是 .
40.(2025·上城模拟)如图,在正方形ABCD中,点E、F分别在边AD、DC上,且,点B关于直线EG的对称点B'在线段BC的延长线上,B'E与BF交于点H。
(1)若点A与点H关于直线BE对称,则 ;
(2)若,则 。
41.(2025·上城模拟)把电阻值分别为,的两电阻并联后接入某电路中,其并联总电阻值R(单位:Ω)满足。当时, 。
42.(2025·定海模拟)若圆锥的底面半径是1,它的侧面展开图的圆心角是直角,则该圆锥的高为 .
43.(2025·定海模拟)哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是 .
44.(2025·杭州模拟) 如图是一张菱形纸片ABCD,点E在AD边上,,把沿直线CE折叠得到,点D'落在DA的延长线上. 若CD'恰好平分,则 °, .
45.(2025·杭州模拟) 如图,的切线PA与直径CB的延长线交于点A,点P为切点,连接PC若 , 则的度数为 °.
46.(2025·西湖模拟)如图是一张菱形纸片,点在边上,,把沿直线折叠得到,点落在的延长线上.若恰好平分,则 °, .
47.(2025·拱墅模拟) 在图中,中,, BD是的角平分线,点在BD上,过点E作,交AB于点.若,,,则 .
48.(2025·拱墅模拟) 若一次函数 的图象过点 ,,其中 ,则 .
49.(2025·临安模拟)如图,是边长为6的等边三角形,点为延长线上一点,,过作所在直线的垂线,垂足为,连结,为中点,则线段的长是 .
50.(2025·温州模拟)某挂饰由圆盘和挂绳组成(如图),AB,AC分别切⊙O于点B,C.若∠A=64°,则的度数为 度.
答案解析部分
1.3
解:∵二次函数 与一次函数 (a是常数)的图象交于两个不同的点A,B,点A的横坐标是
∴二次函数为 一次函数为 令
解得 或
∴点B的横坐标是3.
故答案为:3.
由题意得到 求得 则二次函数为 一次函数为 令 解方程即可求得点B的横坐标.
2.(x+2)(x-2)
解:x2-4=(x+2)(x-2).
故答案为:(x+2)(x-2).
直接利用平方差公式法分解即可。
3.(a-2)(a+2)
原式=(a-2)(a+2).
故答案为(a-2)(a+2).
直接利用平方差公式分解即可.
4.
5.±2
6.x(x+2)
解:原式=x(x+2),
故答案为:x(x+2).
直接利用提公因式法分解即可。
7.x≥2
解:根据题意,使二次根式 有意义,即x﹣2≥0,
解得x≥2;
故答案为:x≥2.
根据二次根式有意义的条件,可得x﹣2≥0,解不等式求范围.
8.
解:
解第一个不等式得:x>-1,
解第二个不等式得:x≤6.
则不等式组的解集是:-1<x≤6,
故答案为:-1<x≤6.
两个不等式的解集的公共部分就是不等式组的解集.
9.
解:m2+m=m(m+1),
故答案为:m(m+1).
由于第一项和第二项相同字母m的最低次方为1,提取公因式m即可。
10.
解:如图,延长AD交BE于点F,
∵AC∶BC=3∶4,
∴设AC=3x,BC=4x,
在Rt△ABC中,AB=,
∵点D是BC的中点,
∴BD=CD=2x,
在Rt△ACD中,AD=;
由翻折得AE=AB=5x,DE=BD=CD=2x,
∴AD是BE的垂直平分线,∠DBE=∠DEB,∠DEC=∠DCE,
∵∠DBE+∠DEB+∠DEC+∠DCE=2(∠BED+∠DEC)=180°,
∴∠BEC=∠BED+∠CED=90°,
∴△BCE是直角三角形,
设DF=y,则AF=AD+DF=,
由勾股定理得AF2=AE2-EF2,EF2=DE2-DF2,
∴AF2=AE2-DE2+DF2,即,
解得,即DF=,
∵∠AFB=∠CEB=90°,
∴DF∥CE,
∴△BDF∽△BCE,
∴,即,
∴
∴,
∵S△ABC=,S△BCE=,
∵点D是BC的中点,
∴S△ACD=S△ABD=,S△CED=,
∴S1=S△ACD+S△CDE=,S2=S△ABD=3x2,
∴.
故答案为:.
延长AD交BE于F,设AC=3x,BC=4x,由勾股定理得AB=5x,AD=;由翻折得AE=AB=5x,DE=BD=CD=2x,根据“到线段两端点的距离相等的点在这条线段的垂直平分线上及两点确定一条直线”得AD是BE的垂直平分线,由等边对等角及三角形的内角定理可推出△BCE是直角三角形,设DF=y,则AF=AD+DF=,由勾股定理可得AF2=AE2-DE2+DF2,据此建立方程求出,即DF=,由同位角相等两直线平行,得DF∥CE,由平行于三角形一边得直线截其它两边,所截三角形与原三角形相似得△BDF∽△BCE,由相似三角形对应边成比例建立方程可得,根据勾股定理表示出BE,然后根据三角形面积计算公式分别计算出△ABC、△BCE的面积,由等底同高三角形面积相等得出△ACD、△ABD、△CED的面积,进而根据S1=S△ACD+S△CDE算出S1,最后再求出两个面积之比即可.
11.
解:从3张分别写着 0,1,2,的卡片中随机的抽取两张,共有0、1,0、2,1、2,三种,其中乘积为0的有0、1与0、2两种,∴ 从中随机抽取2张,数字之积为0的概率是.
故答案为:.
利用列举法列举出从3张分别写着 0,1,2,的卡片中随机的抽取两张的所有情况,再根据有理数乘法法则“任何数与0相乘都等于0”找出其中乘积为0的情况数,从而根据概率公式计算可得答案.
12.
解:由题意可得:BC=AD,∠BAD=90°,
∵将矩形ABCD绕点A顺时针旋转,旋转90°得矩形A1B1C1D1,继续旋转使得点B的对应点B2落在B1D1上,
∴AB=AB1=AB2,∠B1AD1=90°,AD1=AD,
∴点B、B1、B2在以点A为圆心,AB为半径的圆上,
∴,
∵AB=AB1=AB2,
∴,
∠ABB2=∠AB2A,
∵∠B1AD1+∠BAD=180°,
∴B、A、D1在同一直线上,
∵∠B2BD1+∠B2D1B=∠B1B2B=45°,
∠B1BB2+∠B2BA=∠B2BA=45°,
∴∠B1BB2=∠B2D1B,
∵AB:BC=3:4,
∴设AB1=AB=3x,则AD=AD1=BC=4x,
∴,
∴,
故答案为:.
根据矩形的性质得出BC=AD,∠BAD=90°,根据旋转的性质得出AB=AB1=AB2,∠B1AD1= 90°,AD1=AD,证明点B、B1、B2在以点A为圆心,AB为半径的圆上,根据圆周角定理得出,证明,设AB1=AB=3x,则AD=AD1=BC=4x,根据勾股定理得出,根据三角函数定义即可求出答案.
13.2或-2
14.
15.
16.
解:要使分式有意义,则x+1≠0,因此x≠-1
故答案为:x≠-1.
本题考查的是分式有意义的条件:分母不为0即可.
17.
解:
=
故答案为:.
先提取公因式-1,把二次项系数化为正,再利用完全平方公式因式分解即可.
18.
19.4
20.4
21.
22.4
解:∵多边形ABCDEF是正六边形,设AB的长为a,
∴正六边形的面积为,
∵,,
∴,
∴a=4,
则AB的长为4.
故答案为:4.
先求出正六边形的面积,再根据、的占比即可求解.
23.3
解:设点A的坐标为,根据题意:
∵矩形OBAC的周长为8,得:,
∴
对角线OA的长度为,得:
将平方得:
结合,代入得:
10+2k=16
∴k=3
故答案为:3.
利用反比例函数解析式,设点A坐标为,根据矩形周长公式和勾股定理,建立关于a和k的方程组,通过代数变形(如平方展开)消元,最终求出k的值.
24.
解:∵一个口袋里装有4个黑球,3个白球
∴从中任意摸出一个球,摸到黑球的概率为:
故答案为:.
用黑球的个数除以球的总个数即可求得摸到黑球的概率.
25.
解:由条件可知OA=OB=4,
∵∠AOB=45°
∴
∵点P为OB中点,
∴,
由条件可得△OPQ为等腰直角三角形,
∴QP=OP=2,
∴,
∴,
∴阴影部分的周长
故答案为:.
利用弧长公式可得,又由△OPQ为等腰直角三角形可得,即得,进而求出周长即可.
26.
27.
28.2
29.
30.
31.
32.(x-4)2
解:x2-8x+16=(x-4)2.
故答案为:(x-4)2.
直接利用完全平方公式进行分解即可.
33.
解: .
直接应用平方差公式即可求解. .
34.
35.
解:∵△BCE旋转得到△BFG,
∴△BCE △BFG,
∴BC=BF,∠ABH=∠CBE
∵ABCD是菱形,BC=12,
∴AD=BC=AB=CD=12,AD//BC
∴∠DAC=∠BCH,∠AFH=∠CBH,
∴△AFH∽△CBH
∵F是AD的中点,
∴
∴,
∵AB=BC,
∴∠BAC=∠BCA,
在△ABH和△CBE中,
∴△ABH≌△CBE(ASA),
∴BH=BE=8,AH=EC,
∵
∴AH=HE=EC,
过B作BK⊥HE交于点K,
∵BH=BE=8,HE=EC
由等腰三角形三线合一可得HK=KE,
设HK=KE=x,EC=HE=2x,
在Rt△BKE和Rt△BKC中,由勾股定理可得:
BK2=BE2-KE2=BC2-KC2
∴82-x2=122-(x+2x)2,
解得(舍去)或,
∴,
故答案为:.
证明△AFH∽△CBH和△ABH≌△CBE(ASA),并根据等腰三角形三线合一得出HK=KE,进一步在Rt△BKE和Rt△BKC中,由勾股定理可得:BK2=BE2-KE2=BC2-KC2建立方程求解即可得出HE的长.
36.
解:由题意可得,
故答案为:.
利用扇形的面积公式进行计算即可.
37.
解:
如图,过D作DP⊥AB于P
设∠MAC=x,∠C=y
由折叠知,∠MAC=∠DAM=x,∠AMC=90°,DM=MC
∴x+y=90°
∵AN为直径
∴∠ABN=90°
在圆中,∠C=∠N=y
∴∠ABN=90°-y=x
∴∠BAC=3x
∵AB=BC
∴∠BAC=∠BCA
∴3x=y
∴x+y=4x=90°
故x=22.5°
∴∠BAM=45°,
∴△AMB为等腰直角三角形,△DPB也为等腰直角三角形
∵∠BAD=∠MAD,DP⊥AB,DM⊥AM
∴PD=DM
∴
∴
故答案为:.
通过设∠MAC=x,∠C=y,根据折叠知∠AMC=90°,得x+y=90°,利用圆的性质和同角余角相等,进一步求得3x=y,从而求得x=22.5°,因此△BPD为等腰直角三角形,最后利用边的比例关系求解.
38.真
解:
∵(a+c)2b2,
∴a2+2ac+c2≤b2,
∴a2-2ac+c2≤b2-4ac,
∵(a-c)2≤b2-4ac,(a-c)2≥0
∴b2-4ac≥0,
∴关于x的一元二次方程ax2+bx+c=0(a≠0)必有实数根,
∴命题“若(a+c)2≤b2,则关于x的一元二次方程ax2+bx+c=0(a≠0)必有实数根”是真命题,
故答案为:真.
题目通过条件 ( a+c )2 ≤b2推导出判别式△ ≥ (a c)2≥0,从而得出方程必有实根的结论.
39.
解:
∵1~9中2的倍数有2、4、6、8四个数,
∴抽到的卡片上的数是2的倍数的概率是
故答案为:.
先得出2的倍数,再根据概率公式即可得出结论.
40.(1)
(2)
解:(1)∵ 点B关于直线EG的对称点B'在线段BC的延长线上,
∴EB=EB',
∴∠EBB'=∠EB'B,
又∵ABCD是正方形,
∴AD∥BC,∠ABC=90°,
∴∠AEB=∠EBC,
由折叠可得∠AEB=∠B'EB,
∴∠EBB'=∠EB'B=∠BEB'=60°,
∴∠ABE=30°,
∴;
(2)如图,过点B'作B'N∥CD,过点F作FM∥BC交B'E、B'N于点M、N两点,设FM=a,DE=DF=x,则四边形CB'NF为矩形,
∴FN=CB',B'N=CF,
∵B'N∥CD,
∴△HFM∽△HBB',
∴,即,
∵点B关于直线EG的对称点B'在线段BC的延长线上,
∴BG=B'G=6a,EG⊥BC,
∴CD=BC=EG=AB=AD=AE+ED=BG+DE=6a+x,
又∵DF=DE=x,
∴B'N=CF=6a,
又又问我FN=CB'=GB'-CB'=6a-x,
∴MN=FM+FN=a+6a-x=7a-x,
又∵FM∥BC,
∴∠NMB'=∠MB'G,
又∵∠N=∠EGB'=90°,
∴△B'NM∽△EGB',
∴,即,
解得x=3a或x=-2a,
∴;
故答案为:;.
(1)根据正方形的性质和轴对称可得∠EBB'=∠EB'B=∠BEB'=60°,即可求出∠ABE=30°,进而计算正切即可;
(2)过点B'作B'N∥CD,过点F作FM∥BC交B'E、B'N于点M、N两点,设FM=a,DE=DF=x,则四边形CB'NF为矩形,先根据△HFM∽△HBB',求出BB'的长,然后证明△B'NM∽△EGB',利用对应边成比例求出x=3a,然后代入计算比值即可.
41.
解:∵ ,
∴,
∴,
故答案为:.
把 代入计算可得,然后求出比值即可解题.
42.
解:设圆锥的母线长为l,
∵圆锥的底面圆半径为1,
∴圆锥侧面展开图扇形的弧长为,
∵圆锥的侧面展开图的圆心角是直角,
∴,
解得:l=4,
∴圆锥的高为:,
故答案为:.
设圆锥的母线长为l,根据圆锥的侧面展开图扇形的弧长等于圆锥底面圆周长,结合弧长公式得,从而求出l=4,进而利用勾股定理即可求解.
43.
解:列表如下:
2 3 5
2 5 7
3 5 8
5 7 8
∴共有6种等可能结果,其中和是偶数的有2种,
∴随机选取两个不同的数,其和是偶数的概率是,
故答案为:.
利用列表法得出所有的等可能结果数,从而得其中和是偶数的结果数,进而利用概率公式进行计算即可.
44.36;
解:设AB, 交于点J.设∠B=x.
∵四边形ABCD是菱形,
∴∠B=∠D =x,AD∥CB,
∴∠BCD'=∠D',
∵CD'平分∠ACB,
∴∠ACD'=∠BCD',
由翻折变换的性质可知,∠D =∠D',
∴∠BCD'=∠ACD'=x,
∵BA=BC,
∴∠BCA=∠BAC=2x,
∵∠B+∠ACB+∠BAC=180°,
∴5x=180°,
设 , 则.
故答案为:36,
设AB, 交于点J.设. .利用三角形内角和定理构建方程求出x即可,证明设,则 利用相似三角形的性质构建一元二次方程求解.
45.35
解:如图, 连接OP,
∵ PA是⊙O的切线,
由圆周角定理得:
故答案为: 35.
连接OP,根据切线的性质得到 根据直角三角形的性质求出. 再根据圆周角定理解答即可.
46.;
47.
解:作DH⊥AB于点H, 则∠BHD =∠C =90°,
∵BD是∠ABC的角平分线,
∴∠HBD=∠CBD,
∵BD=BD,
∴△HBD≌△CBD(AAS)
∵EF⊥BD于点E,
∴∠BEF = 90°,
∵BE=4, BF=5,
∴BD=BE+DE=4+3=7,
故答案为:
作DH⊥AB于点H, 则∠BHD=∠C=90°, 而∠HBD=∠CBD, BD=BD, 可根据“AAS”证明△HBD≌△CBD,根据勾股定理求得DE =EF=3, 则BD=7, 由余弦的定义求出BH长,即可求出BC长解题.
48.-1
解:∵一次函数 的图象过点(1,m), (m,1),
解得:
故答案为:
利用一次函数图象上点的坐标特征,可得出关于k的方程组,解之即可得出结论.
49.
50.116
解:连接圆心O与切点B、C,
根据切线性质,OB⊥AB,OC⊥AC,
∵四边形ABOC内角和为360°,∠A=64°,∠ABO=∠ACO=90°,
∴∠BOC=360°-64°-90-90°=116°,
∴弧BC的度数为116°,
故答案为:116.
根据切线性质可知∠ABO=∠ACO=90°,再根据四边形内角和即可求解.
同课章节目录
