青岛版六年级下册数学4.1比例尺(课件)(共17张PPT)
文档属性
| 名称 | 青岛版六年级下册数学4.1比例尺(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
4.1比例尺
青岛版小学6年级下册
第四章《快乐足球—比例尺》
一、学习目标
理解比例尺的意义,学会求比例尺,图上距离和实际距离;
经历比例尺产生过程和探究比例尺应用的过程,提高学生解决实际问题的能力。
结合具体情境,使学生体验到数学与生活的密切联系,进一步激发学生学习数学的兴趣。
2
二、问题导入
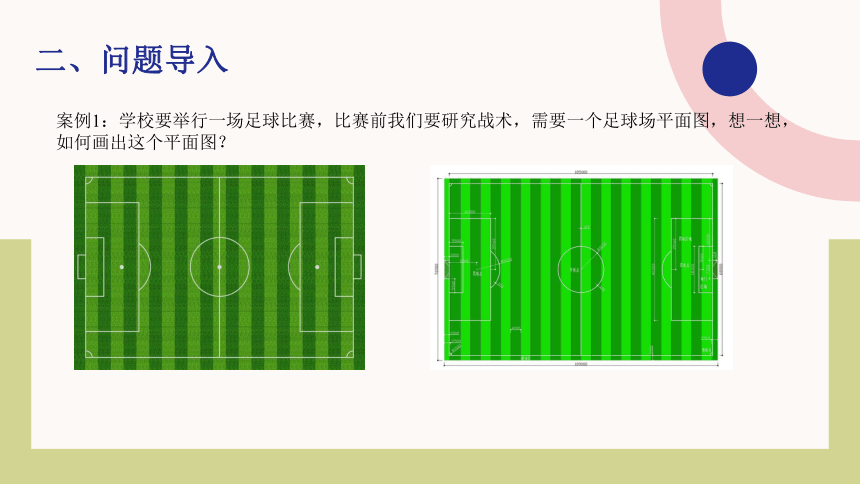
案例1:学校要举行一场足球比赛,比赛前我们要研究战术,需要一个足球场平面图,想一想,如何画出这个平面图?
二、问题导入
案例1:测得足球场地实际距离是:长95米,宽60米;尝试画一画,看看怎样画最像。
不同的长宽我们能画出不同的长方形,如上图所示,在这三个长方形里,长9.5厘米,宽6厘米的长方形是最像足球场的,是将足球场地实际距离的长和宽按照一定比例缩小,用9.5厘米表示95米,用6厘米表示60米。
三、比例尺概念
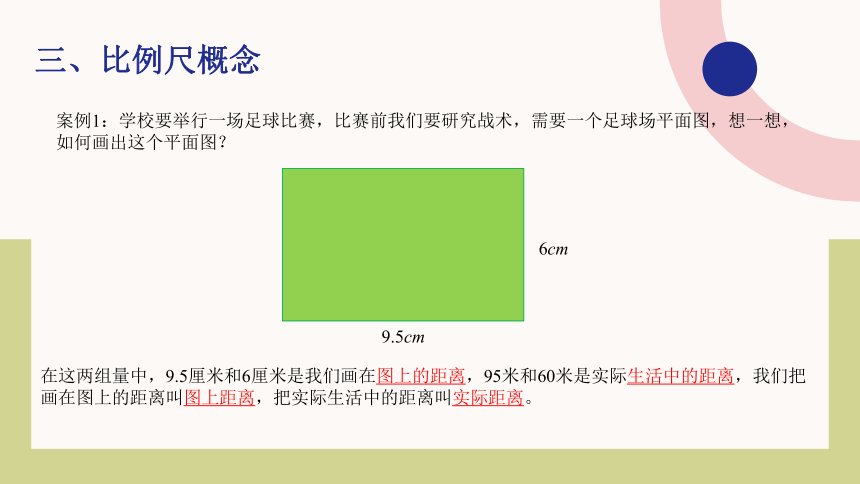
案例1:学校要举行一场足球比赛,比赛前我们要研究战术,需要一个足球场平面图,想一想,如何画出这个平面图?
9.5cm
6cm
在这两组量中,9.5厘米和6厘米是我们画在图上的距离,95米和60米是实际生活中的距离,我们把画在图上的距离叫图上距离,把实际生活中的距离叫实际距离。
三、比例尺概念
案例1:学校要举行一场足球比赛,比赛前我们要研究战术,需要一个足球场平面图,想一想,如何画出这个平面图?
9.5cm
6cm
当我们用9.5厘米表示95米时,实际上把95米缩小了1000倍。这里我们可以看到图上距离与实际距离的比是一定的,1:1000说明我们用图上距离1cm表示了实际距离1000厘米。
像这种图上距离与实际距离的比,就叫比例尺。
图上距离 :实际距离 = 比例尺
图上距离 =实际距离 比例尺
实际距离= 比例尺
三、比例尺概念理解
问题:比例尺1:5000表示图上距离1厘米代表实际距离多少厘米?多少米?
比例尺1:5000意味着图上的1厘米代表着实际的5000厘米,根据100厘米=1米,所以5000厘米
=50米。因此,图上距离1厘米代表实际距离50米。
三、比例尺概念理解
某地图上量得甲、乙两地的图上距离为5厘米,而这两地的实际距离为25千米。求这幅地图的比例尺?
答案:首先,将实际距离从千米转换为厘米,即25千米 = 2500000厘米;
然后,根据比例尺的定义,比例尺 = 图上距离 / 实际距离 = 5厘米 / 2500000厘米 = 1:500000。
比例尺还可以如下图这样表示:这样的比例尺叫线段比例尺。
四、线段比例尺
图中线段比例尺表示图上1厘米表示实际10千米。
有两张地图,比例尺分别为1:25000和1:50000。量得某条河流的长度相同,问哪张地图上的河流表示得更详细?
四、线段比例尺作用
答案:比例尺1:50000的地图表示得更详细,因为它表示的实际范围更小。
问题1:比例尺1:2000表示什么意义?
四、线段比例尺—应用
答案:表示图上1厘米代表实际2000厘米,即20米。
问题2:在比例尺为1:5000的地图上,量得某公园的图上面积为2平方厘米。求该公园的实际面积
四、线段比例尺—应用
答案:实际面积 = 2平方厘米 × (5000厘米/1厘米)^2 = 50,000,000平方厘米 = 50公顷。
问题2:若一幅地图的比例尺为1:10000,图上距离3厘米代表的实际距离是多少米?
四、线段比例尺—应用
答案:实际距离 = 3厘米 × 10000 = 30000厘米 = 300米。
问题3:已知a、b两地的实际距离为8千米,若要在比例尺为1:40000的地图上表示,则a、b两地的图上距离应为多少厘米?
四、线段比例尺—应用
答案:图上距离 = 8千米 × 100000厘米/千米 × 1/40000 = 2厘米。。
问题4:在比例尺为1:200的地图上,一个矩形的长为5厘米,宽为3厘米。求该矩形在实际中的面积。
四、线段比例尺—应用
答案:实际长 = 5厘米 × 200 = 1000厘米 = 10米;实际宽 = 3厘米 × 200 = 600厘米 = 6米;实际面积 = 10米 × 6米 = 60平方米。
问题5:某地图的比例尺为1:30000,图上一条公路的长度为7.5厘米,若另一张地图的比例尺为1:50000,则这条公路在这张地图上的长度是多少厘米?
四、线段比例尺—应用
答案:首先计算实际长度 = 7.5厘米 × 30000 = 225000厘米;再计算在新地图上的长度 = 225000厘米 × 1/50000 = 4.5厘米。
谢谢
4.1比例尺
青岛版小学6年级下册
第四章《快乐足球—比例尺》
一、学习目标
理解比例尺的意义,学会求比例尺,图上距离和实际距离;
经历比例尺产生过程和探究比例尺应用的过程,提高学生解决实际问题的能力。
结合具体情境,使学生体验到数学与生活的密切联系,进一步激发学生学习数学的兴趣。
2
二、问题导入
案例1:学校要举行一场足球比赛,比赛前我们要研究战术,需要一个足球场平面图,想一想,如何画出这个平面图?
二、问题导入
案例1:测得足球场地实际距离是:长95米,宽60米;尝试画一画,看看怎样画最像。
不同的长宽我们能画出不同的长方形,如上图所示,在这三个长方形里,长9.5厘米,宽6厘米的长方形是最像足球场的,是将足球场地实际距离的长和宽按照一定比例缩小,用9.5厘米表示95米,用6厘米表示60米。
三、比例尺概念
案例1:学校要举行一场足球比赛,比赛前我们要研究战术,需要一个足球场平面图,想一想,如何画出这个平面图?
9.5cm
6cm
在这两组量中,9.5厘米和6厘米是我们画在图上的距离,95米和60米是实际生活中的距离,我们把画在图上的距离叫图上距离,把实际生活中的距离叫实际距离。
三、比例尺概念
案例1:学校要举行一场足球比赛,比赛前我们要研究战术,需要一个足球场平面图,想一想,如何画出这个平面图?
9.5cm
6cm
当我们用9.5厘米表示95米时,实际上把95米缩小了1000倍。这里我们可以看到图上距离与实际距离的比是一定的,1:1000说明我们用图上距离1cm表示了实际距离1000厘米。
像这种图上距离与实际距离的比,就叫比例尺。
图上距离 :实际距离 = 比例尺
图上距离 =实际距离 比例尺
实际距离= 比例尺
三、比例尺概念理解
问题:比例尺1:5000表示图上距离1厘米代表实际距离多少厘米?多少米?
比例尺1:5000意味着图上的1厘米代表着实际的5000厘米,根据100厘米=1米,所以5000厘米
=50米。因此,图上距离1厘米代表实际距离50米。
三、比例尺概念理解
某地图上量得甲、乙两地的图上距离为5厘米,而这两地的实际距离为25千米。求这幅地图的比例尺?
答案:首先,将实际距离从千米转换为厘米,即25千米 = 2500000厘米;
然后,根据比例尺的定义,比例尺 = 图上距离 / 实际距离 = 5厘米 / 2500000厘米 = 1:500000。
比例尺还可以如下图这样表示:这样的比例尺叫线段比例尺。
四、线段比例尺
图中线段比例尺表示图上1厘米表示实际10千米。
有两张地图,比例尺分别为1:25000和1:50000。量得某条河流的长度相同,问哪张地图上的河流表示得更详细?
四、线段比例尺作用
答案:比例尺1:50000的地图表示得更详细,因为它表示的实际范围更小。
问题1:比例尺1:2000表示什么意义?
四、线段比例尺—应用
答案:表示图上1厘米代表实际2000厘米,即20米。
问题2:在比例尺为1:5000的地图上,量得某公园的图上面积为2平方厘米。求该公园的实际面积
四、线段比例尺—应用
答案:实际面积 = 2平方厘米 × (5000厘米/1厘米)^2 = 50,000,000平方厘米 = 50公顷。
问题2:若一幅地图的比例尺为1:10000,图上距离3厘米代表的实际距离是多少米?
四、线段比例尺—应用
答案:实际距离 = 3厘米 × 10000 = 30000厘米 = 300米。
问题3:已知a、b两地的实际距离为8千米,若要在比例尺为1:40000的地图上表示,则a、b两地的图上距离应为多少厘米?
四、线段比例尺—应用
答案:图上距离 = 8千米 × 100000厘米/千米 × 1/40000 = 2厘米。。
问题4:在比例尺为1:200的地图上,一个矩形的长为5厘米,宽为3厘米。求该矩形在实际中的面积。
四、线段比例尺—应用
答案:实际长 = 5厘米 × 200 = 1000厘米 = 10米;实际宽 = 3厘米 × 200 = 600厘米 = 6米;实际面积 = 10米 × 6米 = 60平方米。
问题5:某地图的比例尺为1:30000,图上一条公路的长度为7.5厘米,若另一张地图的比例尺为1:50000,则这条公路在这张地图上的长度是多少厘米?
四、线段比例尺—应用
答案:首先计算实际长度 = 7.5厘米 × 30000 = 225000厘米;再计算在新地图上的长度 = 225000厘米 × 1/50000 = 4.5厘米。
谢谢
