7.2 离散型随机变量及其分布列--2025人教A版数学选择性必修第三册同步练习题(含解析)
文档属性
| 名称 | 7.2 离散型随机变量及其分布列--2025人教A版数学选择性必修第三册同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 10:13:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教A版数学选择性必修第三册
7.2 离散型随机变量及其分布列
A级 必备知识基础练
1.[探究点一]一个袋子中有除颜色外其他都相同的红、黄、绿、白四种小球各若干个,一次倒出3个小球,下列变量是离散型随机变量的是( )
A.小球滚出的最大距离
B.倒出小球所需的时间
C.倒出的3个小球的质量之和
D.倒出的3个小球的颜色的种数
2.[探究点三]设某项试验成功的概率是失败概率的2倍,记Y=则P(Y=0)=( )
A.0 B.
C. D.
3.[探究点二·2024安徽滁州高二期中]若随机变量X的分布列为
X -2 -1 0 1 2 3
P 0.1 0.2 0.1 0.3 0.1 0.2
则当P(XA.(-∞,2] B.[1,2] C.(1,2] D.(1,2)
4.[探究点二]设离散型随机变量X的分布列为
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
若随机变量Y=X-2,则P(Y=2)=( )
A.0.3 B.0.4 C.0.6 D.0.7
5.[探究点二]一盒中有10个羽毛球,其中8个新的,2个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球的个数X是一个随机变量,其分布列为P(X),则P(X=4)=( )
A. B.
C. D.
6.[探究点一]甲进行3次射击,甲每次射击击中目标的概率为,记甲击中目标的次数为X,则X的可能取值为 .
7.[探究点二]一批产品分为一、二、三级,其中一级品数量是二级品的两倍,三级品数量为二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量X,则P≤X≤= .
8.[探究点二]某学生参加一次考试,已知在备选的10道试题中,能答对其中的6道题.规定每次考试都从备选题中随机抽出3道题进行测试,求该生答对试题数X的分布列.
B级 必备知识基础练
9.(多选题)已知随机变量X的分布列为P(X=n)=(n=0,1,2),其中a是常数,则 ( )
A.P(X=0)+P(X=1)+P(X=2)=1
B.a=
C.P(0≤X<2)=
D.P(X=2)=
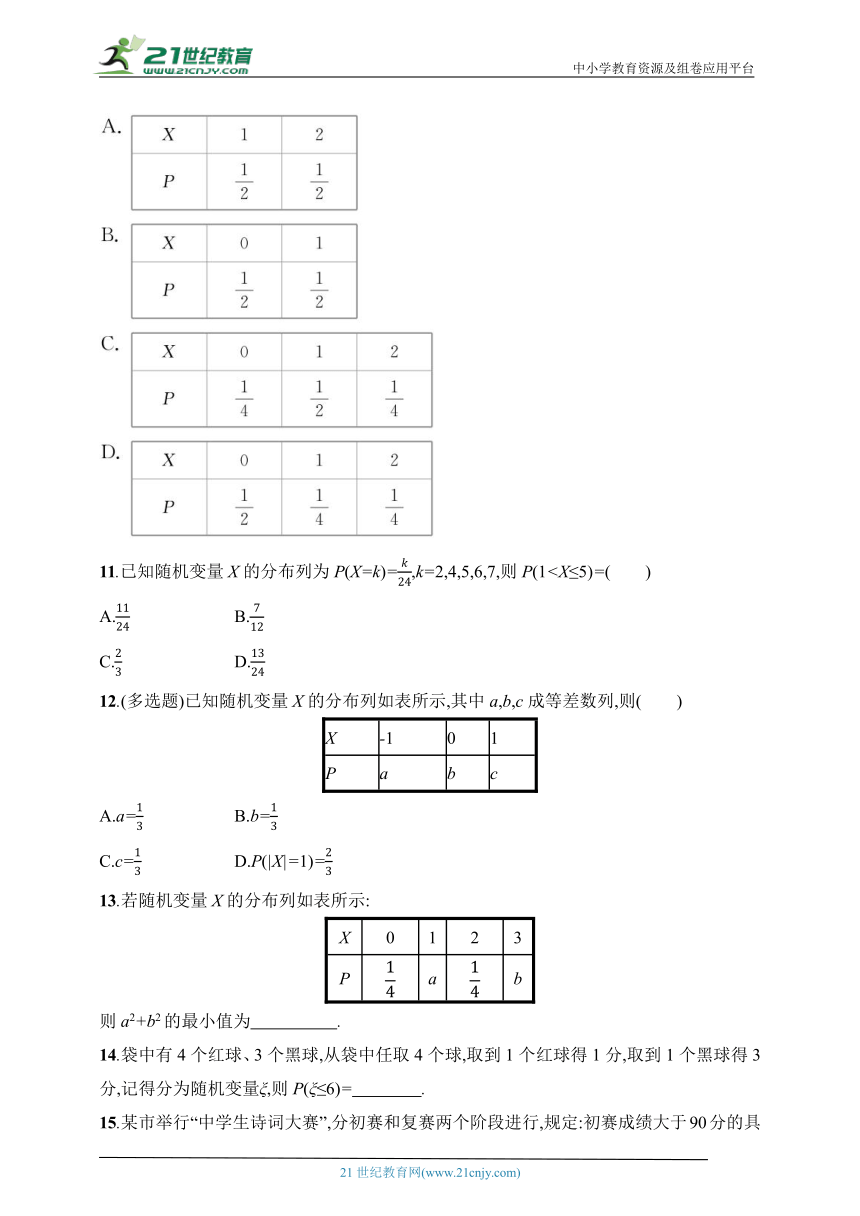
10.[2024河南新乡高二统考]投掷两枚质地均匀的骰子,记偶数点朝上的骰子的个数为X,则X的分布列为( )
11.已知随机变量X的分布列为P(X=k)=,k=2,4,5,6,7,则P(1A. B.
C. D.
12.(多选题)已知随机变量X的分布列如表所示,其中a,b,c成等差数列,则( )
X -1 0 1
P a b c
A.a= B.b=
C.c= D.P(|X|=1)=
13.若随机变量X的分布列如表所示:
X 0 1 2 3
P a b
则a2+b2的最小值为 .
14.袋中有4个红球、3个黑球,从袋中任取4个球,取到1个红球得1分,取到1个黑球得3分,记得分为随机变量ξ,则P(ξ≤6)= .
15.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
(1)求获得复赛资格的人数.
(2)从初赛得分在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间(110,130]与(130,150]中分别抽取多少人
(3)从(2)抽取的7人中,选出3人参加全市座谈交流,设X表示得分在区间(130,150]中参加全市座谈交流的人数,求X的分布列.
16.[2024广东汕尾高二期末]在某校举办的知识能力测评中,随机抽查了100名学生,其中有4名女生和3名男生的成绩在90分以上,从这7名同学中每次随机抽1人在全校进行经验分享,每位同学最多分享一次,记第一次抽到女生为事件A,第二次抽到男生为事件B.
(1)求P(B),P(B|A);
(2)若把抽取学生的方式更改为“从这7名学生中随机抽取3人进行经验分享”,记被抽取的3人中女生的人数为X,求X的分布列.
C级 学科素养创新练
17.袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
(1)求袋中所有的白球的个数;
(2)求随机变量ξ的分布列;
(3)求甲取到白球的概率.
参考答案
7.2 离散型随机变量及其分布列
1.D 对于A,小球滚出的最大距离不是离散型随机变量,因为滚出的最大距离不能一一列出;对于B,倒出小球所需的时间不是离散型随机变量,因为所需的时间不能一一列出;对于C,3个小球的质量之和是一个定值,不是随机变量;对于D,倒出的3个小球的颜色的种数可以一一列出,是离散型随机变量.
2.C 设P(Y=1)=p,则P(Y=0)=1-p.又p=2(1-p),解得p=,故P(Y=0)=
3.C 由随机变量X的分布列知:
P(X<-1)=0.1,P(X<0)=0.3,P(X<1)=0.4,P(X<2)=0.7,
则当P(X4.A 由题得,0.2+0.1+0.1+0.3+m=1,解得m=0.3.又P(Y=2)=P(X=4)=0.3,故选A.
5.A ∵从盒子中任取3个球来用,用完后装回盒中,此时盒中旧球个数X=4,即旧球的个数增加了2个,
∴取出的3个球中必有2个新球,
即取出的3个球必为1个旧球,2个新球,
∴P(X=4)=
故选A.
6.0,1,2,3
7 设二级品有k个,则一级品有2k个,三级品有个,总数为个.
∴X的分布列为
X 1 2 3
P
∴PX=P(X=1)=
8.解 答对试题数X的可能取值为0,1,2,3,
则P(X=0)=,P(X=1)=,
P(X=2)=,P(X=3)=
所以该生答对试题数X的分布列为
X 0 1 2 3
P
9.ABC 根据题意,随机变量X的分布列为
P(X=n)=(n=0,1,2),
则P(X=0)+P(X=1)+P(X=2)==1,
解得a=,
则P(0≤X<2)=P(X=0)+P(X=1)=,P(X=2)=
10.C 因为每枚骰子偶数点朝上的概率为,且相互独立,X的取值可能为0,1,2.
P(X=0)=,P(X=1)=2,P(X=2)=,
所以X的分布列为
X 0 1 2
P
故选C.
11.A 由题意可知,P(112.BD ∵a,b,c成等差数列,
∴2b=a+c.
由分布列的性质得a+b+c=3b=1,
∴b=
∴P(|X|=1)=P(X=1)+P(X=-1)=1-P(X=0)=1-
13 由分布列的性质,知a+b=
又a2+b2当且仅当a=b=时,等号成立,则a2+b2的最小值为
14 取出的4个球中红球的个数可能为4,3,2,1,相应的黑球的个数为0,1,2,3,其得分ξ=4,6,8,10,则P(ξ≤6)=P(ξ=4)+P(ξ=6)=
15.解(1)由题意知在区间(90,110]的频率为1-20×(0.002 5+0.005+0.007 5×2+0.012 5)=0.3,0.3+(0.012 5+0.005)×20=0.65,故获得复赛资格的人数为800×0.65=520.
(2)0.012 5∶0.005=5∶2,在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人,
则在区间(110,130]与(130,150]中分别抽取5人,2人.
(3)X的可能取值为0,1,2,则
P(X=0)=,
P(X=1)=,
P(X=2)=
故X的分布列为
X 0 1 2
P
16.解 (1)由题意可得,P(A)=
“第一次抽到女生且第二次抽到男生”就是事件AB,“第一次抽到男生且第二次抽到男生”就是事件B,从7个同学中每次不放回地随机抽取2人,试验的样本空间包含=7×6=42个等可能的样本点.
因为n(AB)==4×3=12,n(B)==6,
所以P(B)=,P(AB)=,
故P(B|A)=
(2)被抽取的3人中女生人数X的取值为0,1,2,3,
P(X=0)=,P(X=1)=,
P(X=2)=,P(X=3)=,
则X的分布列为
X 0 1 2 3
P
17.解 (1)设袋中原有n个白球,由题意知
可得n=3或n=-2(舍去),即袋中原有3个白球.
(2)由题意,ξ的可能取值为1,2,3,4,5.
P(ξ=1)=,
P(ξ=2)=,
P(ξ=3)=,
P(ξ=4)=,
P(ξ=5)=
所以ξ的分布列为
ξ 1 2 3 4 5
P
(3)因为甲先取,所以甲只有可能在第一次、第三次和第五次取到白球,记“甲取到白球”为事件A,则P(A)=P(ξ=1)+P(ξ=3)+P(ξ=5)=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版数学选择性必修第三册
7.2 离散型随机变量及其分布列
A级 必备知识基础练
1.[探究点一]一个袋子中有除颜色外其他都相同的红、黄、绿、白四种小球各若干个,一次倒出3个小球,下列变量是离散型随机变量的是( )
A.小球滚出的最大距离
B.倒出小球所需的时间
C.倒出的3个小球的质量之和
D.倒出的3个小球的颜色的种数
2.[探究点三]设某项试验成功的概率是失败概率的2倍,记Y=则P(Y=0)=( )
A.0 B.
C. D.
3.[探究点二·2024安徽滁州高二期中]若随机变量X的分布列为
X -2 -1 0 1 2 3
P 0.1 0.2 0.1 0.3 0.1 0.2
则当P(X
4.[探究点二]设离散型随机变量X的分布列为
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
若随机变量Y=X-2,则P(Y=2)=( )
A.0.3 B.0.4 C.0.6 D.0.7
5.[探究点二]一盒中有10个羽毛球,其中8个新的,2个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球的个数X是一个随机变量,其分布列为P(X),则P(X=4)=( )
A. B.
C. D.
6.[探究点一]甲进行3次射击,甲每次射击击中目标的概率为,记甲击中目标的次数为X,则X的可能取值为 .
7.[探究点二]一批产品分为一、二、三级,其中一级品数量是二级品的两倍,三级品数量为二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量X,则P≤X≤= .
8.[探究点二]某学生参加一次考试,已知在备选的10道试题中,能答对其中的6道题.规定每次考试都从备选题中随机抽出3道题进行测试,求该生答对试题数X的分布列.
B级 必备知识基础练
9.(多选题)已知随机变量X的分布列为P(X=n)=(n=0,1,2),其中a是常数,则 ( )
A.P(X=0)+P(X=1)+P(X=2)=1
B.a=
C.P(0≤X<2)=
D.P(X=2)=
10.[2024河南新乡高二统考]投掷两枚质地均匀的骰子,记偶数点朝上的骰子的个数为X,则X的分布列为( )
11.已知随机变量X的分布列为P(X=k)=,k=2,4,5,6,7,则P(1
C. D.
12.(多选题)已知随机变量X的分布列如表所示,其中a,b,c成等差数列,则( )
X -1 0 1
P a b c
A.a= B.b=
C.c= D.P(|X|=1)=
13.若随机变量X的分布列如表所示:
X 0 1 2 3
P a b
则a2+b2的最小值为 .
14.袋中有4个红球、3个黑球,从袋中任取4个球,取到1个红球得1分,取到1个黑球得3分,记得分为随机变量ξ,则P(ξ≤6)= .
15.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
(1)求获得复赛资格的人数.
(2)从初赛得分在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间(110,130]与(130,150]中分别抽取多少人
(3)从(2)抽取的7人中,选出3人参加全市座谈交流,设X表示得分在区间(130,150]中参加全市座谈交流的人数,求X的分布列.
16.[2024广东汕尾高二期末]在某校举办的知识能力测评中,随机抽查了100名学生,其中有4名女生和3名男生的成绩在90分以上,从这7名同学中每次随机抽1人在全校进行经验分享,每位同学最多分享一次,记第一次抽到女生为事件A,第二次抽到男生为事件B.
(1)求P(B),P(B|A);
(2)若把抽取学生的方式更改为“从这7名学生中随机抽取3人进行经验分享”,记被抽取的3人中女生的人数为X,求X的分布列.
C级 学科素养创新练
17.袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
(1)求袋中所有的白球的个数;
(2)求随机变量ξ的分布列;
(3)求甲取到白球的概率.
参考答案
7.2 离散型随机变量及其分布列
1.D 对于A,小球滚出的最大距离不是离散型随机变量,因为滚出的最大距离不能一一列出;对于B,倒出小球所需的时间不是离散型随机变量,因为所需的时间不能一一列出;对于C,3个小球的质量之和是一个定值,不是随机变量;对于D,倒出的3个小球的颜色的种数可以一一列出,是离散型随机变量.
2.C 设P(Y=1)=p,则P(Y=0)=1-p.又p=2(1-p),解得p=,故P(Y=0)=
3.C 由随机变量X的分布列知:
P(X<-1)=0.1,P(X<0)=0.3,P(X<1)=0.4,P(X<2)=0.7,
则当P(X
5.A ∵从盒子中任取3个球来用,用完后装回盒中,此时盒中旧球个数X=4,即旧球的个数增加了2个,
∴取出的3个球中必有2个新球,
即取出的3个球必为1个旧球,2个新球,
∴P(X=4)=
故选A.
6.0,1,2,3
7 设二级品有k个,则一级品有2k个,三级品有个,总数为个.
∴X的分布列为
X 1 2 3
P
∴PX=P(X=1)=
8.解 答对试题数X的可能取值为0,1,2,3,
则P(X=0)=,P(X=1)=,
P(X=2)=,P(X=3)=
所以该生答对试题数X的分布列为
X 0 1 2 3
P
9.ABC 根据题意,随机变量X的分布列为
P(X=n)=(n=0,1,2),
则P(X=0)+P(X=1)+P(X=2)==1,
解得a=,
则P(0≤X<2)=P(X=0)+P(X=1)=,P(X=2)=
10.C 因为每枚骰子偶数点朝上的概率为,且相互独立,X的取值可能为0,1,2.
P(X=0)=,P(X=1)=2,P(X=2)=,
所以X的分布列为
X 0 1 2
P
故选C.
11.A 由题意可知,P(1
∴2b=a+c.
由分布列的性质得a+b+c=3b=1,
∴b=
∴P(|X|=1)=P(X=1)+P(X=-1)=1-P(X=0)=1-
13 由分布列的性质,知a+b=
又a2+b2当且仅当a=b=时,等号成立,则a2+b2的最小值为
14 取出的4个球中红球的个数可能为4,3,2,1,相应的黑球的个数为0,1,2,3,其得分ξ=4,6,8,10,则P(ξ≤6)=P(ξ=4)+P(ξ=6)=
15.解(1)由题意知在区间(90,110]的频率为1-20×(0.002 5+0.005+0.007 5×2+0.012 5)=0.3,0.3+(0.012 5+0.005)×20=0.65,故获得复赛资格的人数为800×0.65=520.
(2)0.012 5∶0.005=5∶2,在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人,
则在区间(110,130]与(130,150]中分别抽取5人,2人.
(3)X的可能取值为0,1,2,则
P(X=0)=,
P(X=1)=,
P(X=2)=
故X的分布列为
X 0 1 2
P
16.解 (1)由题意可得,P(A)=
“第一次抽到女生且第二次抽到男生”就是事件AB,“第一次抽到男生且第二次抽到男生”就是事件B,从7个同学中每次不放回地随机抽取2人,试验的样本空间包含=7×6=42个等可能的样本点.
因为n(AB)==4×3=12,n(B)==6,
所以P(B)=,P(AB)=,
故P(B|A)=
(2)被抽取的3人中女生人数X的取值为0,1,2,3,
P(X=0)=,P(X=1)=,
P(X=2)=,P(X=3)=,
则X的分布列为
X 0 1 2 3
P
17.解 (1)设袋中原有n个白球,由题意知
可得n=3或n=-2(舍去),即袋中原有3个白球.
(2)由题意,ξ的可能取值为1,2,3,4,5.
P(ξ=1)=,
P(ξ=2)=,
P(ξ=3)=,
P(ξ=4)=,
P(ξ=5)=
所以ξ的分布列为
ξ 1 2 3 4 5
P
(3)因为甲先取,所以甲只有可能在第一次、第三次和第五次取到白球,记“甲取到白球”为事件A,则P(A)=P(ξ=1)+P(ξ=3)+P(ξ=5)=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
