华师大版七下数学公开课9.1.2《三角形的内角和与外角和》课件(共33张PPT)
文档属性
| 名称 | 华师大版七下数学公开课9.1.2《三角形的内角和与外角和》课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 676.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-15 00:00:00 | ||
图片预览







文档简介
课件33张PPT。预习导视:
1. 三角形的内角和是多少度?
2.三角形的外角与不相邻的内角有什么关系?
3. 什么是三角形的外角和?三角形的外角和是多少度??1.三角形内角和是多少度?撕一撕
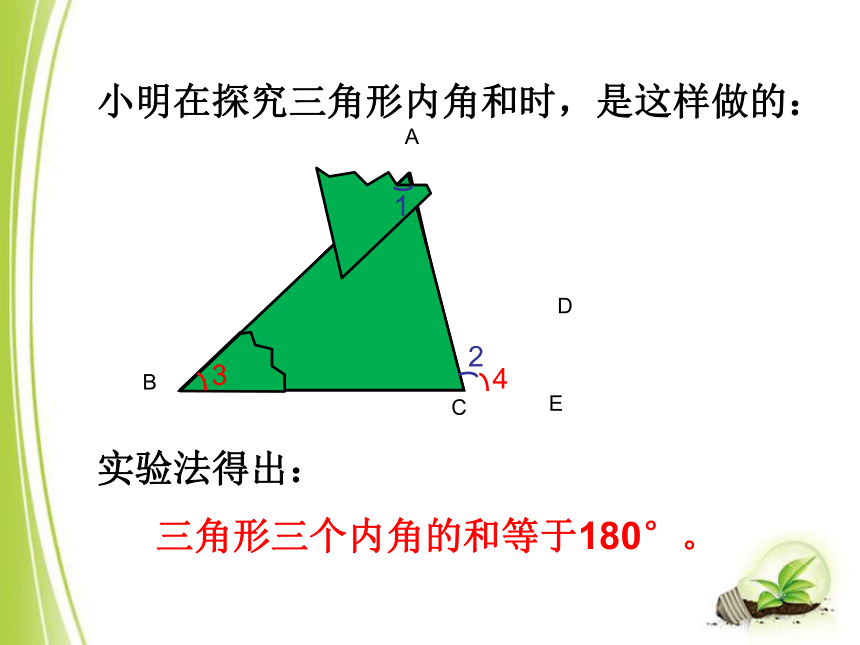
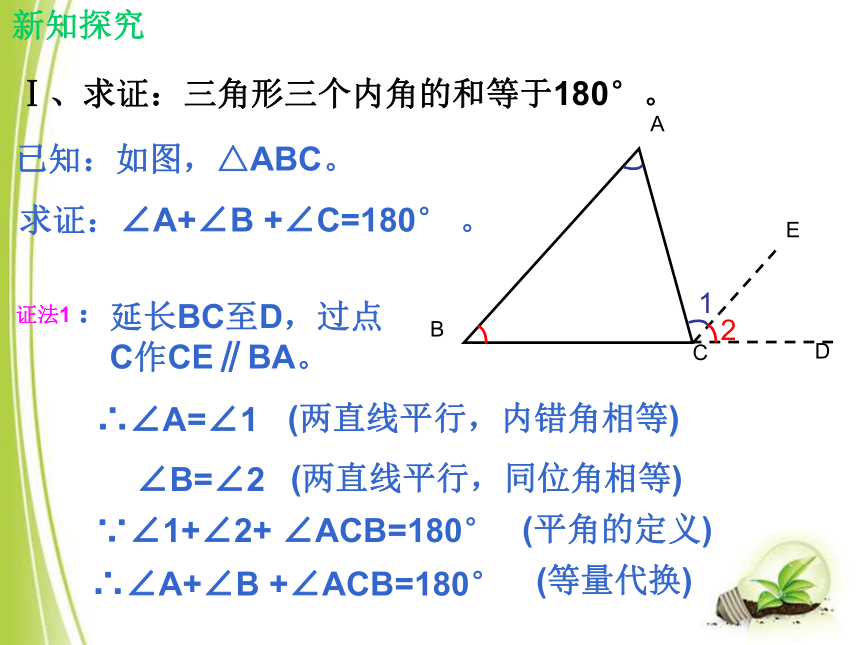
拼一拼活动一: 小明在探究三角形内角和时,是这样做的:ABCDE 实验法得出: 三角形三个内角的和等于180°。Ⅰ、求证:三角形三个内角的和等于180°。新知探究已知:如图,△ABC。求证:∠A+∠B +∠C=180° 。证法1 :∴∠A=∠1 (两直线平行,内错角相等)延长BC至D,过点
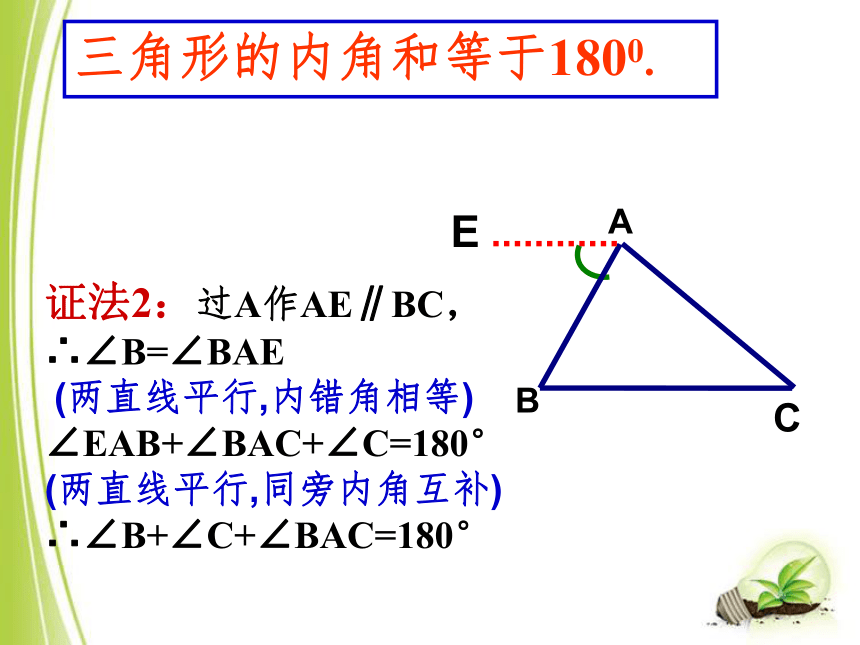
C作CE∥BA。∵∠1+∠2+ ∠ACB=180°(平角的定义)∴∠A+∠B +∠ACB=180°(等量代换) ∠B=∠2 (两直线平行,同位角相等)DE证法2:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
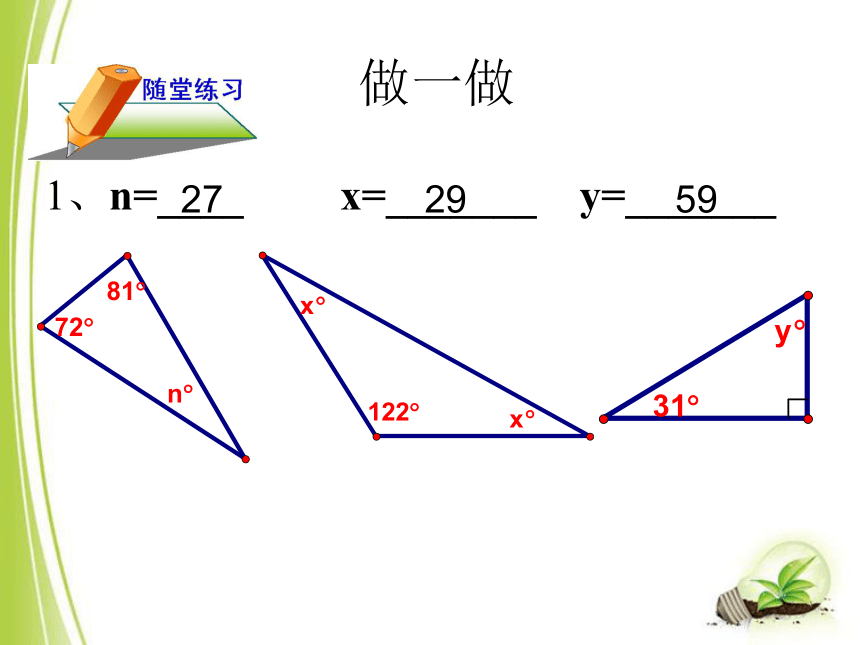
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.三角形的内角和定理三角形的内角和等于180度。做一做1、n=____ x=_______ y=_______272959
2、三角形中至少有_个锐角,最多有_个直角,最多有_个钝角。
3、在△ABC中,若 ∠A:∠B:∠C=2:3:4则∠A= __, ∠B=__, ∠C=__280060014001直角三角形的两个锐角互余。 结论 ?2、在直角三角形中, ∠C是直角,则∠A与∠B的和是多少?返回在Rt △ABC中, ∠C=900 ∴ ∠A+ ∠B=900?2.三角形的外角与不相邻的内角有什么关系?外角2、三角形外角与内角的关系(1)位置关系(2)数量关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角提问1、什么是三角形的外角?思考三角形的外角与它不相邻的内角之间有什么关系呢?在一张白纸上画出如图所示的图形,然后把∠1、 ∠ 2剪下拼在一起,放到∠ 4上,看看会出现什么结果?做一做为什么?发现: ∠1+∠2=∠4思考:如何说明∠ACD= ∠B+ ∠ AD方法一方法二D∠ACD+ ∠ACB=180°∠A+ ∠B+ ∠ACB=180°所以, ∠A+ ∠B= ∠ACD 解:返回三角形的一个外角与三角形三个内角之间有何关系?三角形的一个外角等于与它不相邻的两个内角的和。三角形的外角大于任何一个与它不相邻的内角。∠ACD> ∠ A∠ACD> ∠ B外角+相邻的内角=180 ?返回1.求下列各图中∠1的度数 (并说明理由)2.判断∠1与∠3的大小,并说明理由。∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1解:∠3 > ∠1?3.什么是三角形的外角和?三角形的外角和 对于三角形的每个内角,从与它相邻的两个外角中取一个,这样取得的三个外角相加所得的和,叫做三角形的外角和。思考:三角形的内角和等于180°,那么三角形的外角和等于多少度?返回归纳结论:三角形的外角和等于3600证明:∵∠1+∠ABC=1800 , ∠2+∠BAC=1800 , ∠3+∠ACB=1800
∴ ∠1+∠ABC+ ∠2+ ∠BAC+ ∠3+∠ACB=5400
又∵∠ABC+∠BAC+∠ACB=1800
∴ ∠1+∠2+ ∠3=5400 –
(∠ABC+ ∠BAC+ ∠ACB)=3600 三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( ) A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解:设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? 120? 160 ? , 则相邻的内角分
别为100 ? 60 ? 20 ? 故选 CC例1 如图,D是△ABC的边BC上一点,∠B=∠BAD, ∠ADC=80 ? , ∠BAC=70?. 求:解 :(1)∵∠ADC=∠B+∠BAD=80?
(三角形的一 个外角等于与它不相邻的两个内角的和)又∵ ∠B=∠BAD(已知)(2)∵∠ B+ ∠ BAC+ ∠ C= 180 ? ∴∠ C= 180 ? - ∠ B - ∠ BAC= 180 ? -40 ? -70 ?
=70 ?(三角形的内角和为180 ? )(1) ∠ B的度数;(2) ∠ C的度数。ABDC80 ?(等式的性质)3.三角形的外角性质:1.三角形的内角和等于多少度?4.三角形的外角和等于多少度?5 .在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。我们的收获2.直角三角形的两个锐角是什么关系?②三角形的一个外角等于与它不相邻的两个内角的和。③三角形的外角大于任何一个与它不相邻的内角。①外角+相邻的内角=180 ?下节课部分提高题如图,计算∠BOC让 我 们 一 起 去 发 现CBOACBOA如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?12解:∵∠1= ∠A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又∵∠2= ∠B+ ∠E(三角形的外角等于与它不相邻的两内角的和)∴ ∠A+∠B+∠C+∠D+∠E=(∠A+ ∠D)+(∠B+ ∠E)+∠C=∠1+∠2+∠C=180°挑战!!!提高作业1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______提高作业2、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?提高作业3、如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
1. 三角形的内角和是多少度?
2.三角形的外角与不相邻的内角有什么关系?
3. 什么是三角形的外角和?三角形的外角和是多少度??1.三角形内角和是多少度?撕一撕
拼一拼活动一: 小明在探究三角形内角和时,是这样做的:ABCDE 实验法得出: 三角形三个内角的和等于180°。Ⅰ、求证:三角形三个内角的和等于180°。新知探究已知:如图,△ABC。求证:∠A+∠B +∠C=180° 。证法1 :∴∠A=∠1 (两直线平行,内错角相等)延长BC至D,过点
C作CE∥BA。∵∠1+∠2+ ∠ACB=180°(平角的定义)∴∠A+∠B +∠ACB=180°(等量代换) ∠B=∠2 (两直线平行,同位角相等)DE证法2:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.三角形的内角和定理三角形的内角和等于180度。做一做1、n=____ x=_______ y=_______272959
2、三角形中至少有_个锐角,最多有_个直角,最多有_个钝角。
3、在△ABC中,若 ∠A:∠B:∠C=2:3:4则∠A= __, ∠B=__, ∠C=__280060014001直角三角形的两个锐角互余。 结论 ?2、在直角三角形中, ∠C是直角,则∠A与∠B的和是多少?返回在Rt △ABC中, ∠C=900 ∴ ∠A+ ∠B=900?2.三角形的外角与不相邻的内角有什么关系?外角2、三角形外角与内角的关系(1)位置关系(2)数量关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角提问1、什么是三角形的外角?思考三角形的外角与它不相邻的内角之间有什么关系呢?在一张白纸上画出如图所示的图形,然后把∠1、 ∠ 2剪下拼在一起,放到∠ 4上,看看会出现什么结果?做一做为什么?发现: ∠1+∠2=∠4思考:如何说明∠ACD= ∠B+ ∠ AD方法一方法二D∠ACD+ ∠ACB=180°∠A+ ∠B+ ∠ACB=180°所以, ∠A+ ∠B= ∠ACD 解:返回三角形的一个外角与三角形三个内角之间有何关系?三角形的一个外角等于与它不相邻的两个内角的和。三角形的外角大于任何一个与它不相邻的内角。∠ACD> ∠ A∠ACD> ∠ B外角+相邻的内角=180 ?返回1.求下列各图中∠1的度数 (并说明理由)2.判断∠1与∠3的大小,并说明理由。∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1解:∠3 > ∠1?3.什么是三角形的外角和?三角形的外角和 对于三角形的每个内角,从与它相邻的两个外角中取一个,这样取得的三个外角相加所得的和,叫做三角形的外角和。思考:三角形的内角和等于180°,那么三角形的外角和等于多少度?返回归纳结论:三角形的外角和等于3600证明:∵∠1+∠ABC=1800 , ∠2+∠BAC=1800 , ∠3+∠ACB=1800
∴ ∠1+∠ABC+ ∠2+ ∠BAC+ ∠3+∠ACB=5400
又∵∠ABC+∠BAC+∠ACB=1800
∴ ∠1+∠2+ ∠3=5400 –
(∠ABC+ ∠BAC+ ∠ACB)=3600 三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( ) A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解:设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? 120? 160 ? , 则相邻的内角分
别为100 ? 60 ? 20 ? 故选 CC例1 如图,D是△ABC的边BC上一点,∠B=∠BAD, ∠ADC=80 ? , ∠BAC=70?. 求:解 :(1)∵∠ADC=∠B+∠BAD=80?
(三角形的一 个外角等于与它不相邻的两个内角的和)又∵ ∠B=∠BAD(已知)(2)∵∠ B+ ∠ BAC+ ∠ C= 180 ? ∴∠ C= 180 ? - ∠ B - ∠ BAC= 180 ? -40 ? -70 ?
=70 ?(三角形的内角和为180 ? )(1) ∠ B的度数;(2) ∠ C的度数。ABDC80 ?(等式的性质)3.三角形的外角性质:1.三角形的内角和等于多少度?4.三角形的外角和等于多少度?5 .在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。我们的收获2.直角三角形的两个锐角是什么关系?②三角形的一个外角等于与它不相邻的两个内角的和。③三角形的外角大于任何一个与它不相邻的内角。①外角+相邻的内角=180 ?下节课部分提高题如图,计算∠BOC让 我 们 一 起 去 发 现CBOACBOA如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?12解:∵∠1= ∠A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又∵∠2= ∠B+ ∠E(三角形的外角等于与它不相邻的两内角的和)∴ ∠A+∠B+∠C+∠D+∠E=(∠A+ ∠D)+(∠B+ ∠E)+∠C=∠1+∠2+∠C=180°挑战!!!提高作业1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______提高作业2、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?提高作业3、如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
