数学:第一章实数复习课件(湘教版八年级上)
文档属性
| 名称 | 数学:第一章实数复习课件(湘教版八年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-15 20:30:00 | ||
图片预览




文档简介
课件31张PPT。第1章 实数复习内容:
一、实数的分类
二、有理数的有关概念
1、负数
2、数轴
3、相反数
4、倒数
5、绝对值
6、近似数和有效数字
7、科学记数法
8、方根
9、三种重要的非负性
三.实数
1、有关平方根和立方根
2、实数的运算3、实数的比较大小
4、数字规律探究
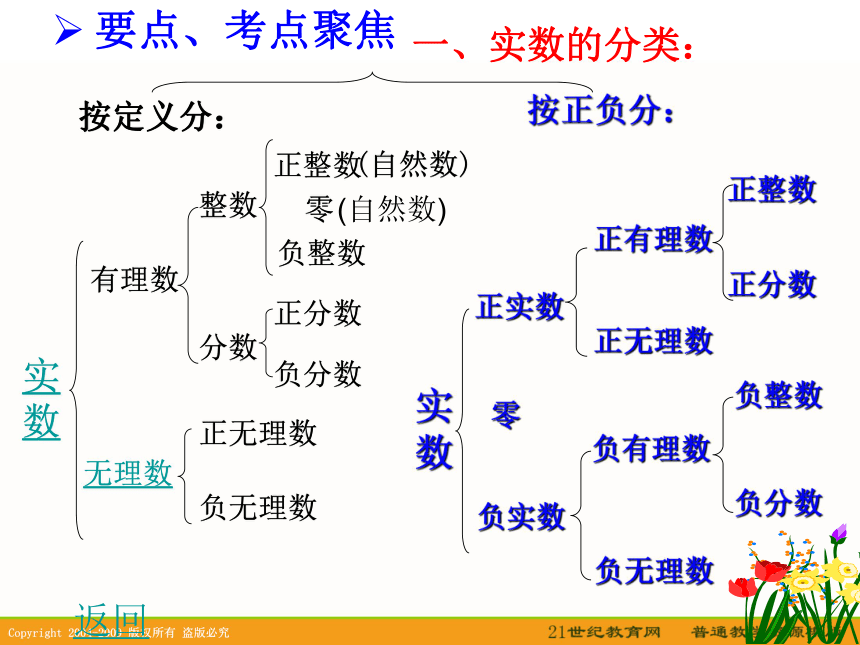
5、零指数,负整指数按定义分:要点、考点聚焦按正负分:一、实数的分类:实数有理数整数正整数(自然数)零负整数分数正分数负分数无理数正无理数负无理数负无理数负分数负整数负有理数负实数零正无理数正分数正整数正有理数正实数实数(自然数)返回考题: 1、写出一个无理数,使它与 的积是有理
数:________c3无限不循环小数叫做无理数
( 强调: 无限 、 不循环.)
无理数常见的4种典型:注意:(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)(4)、三角函数型:tan60°,sin45 °... 返回二、实数的基本概念一.负数:在正数前面加“—”的数;0既不是正数,也不是负数。1、判断:
1)a一定是正数; ( )
2)-a一定是负数; ( )
3)-(-a)一定大于0; ( )
4)0是正整数。 ( )××××2、(1)如果零上5℃记作5℃,则零下2℃记作_____
(2) 如果上升10m记作10m,那么-5m表示____
(3)比海平面低35m的地方,它的高度是海拔___ 数轴上的点与_____是一一对应的。二、实数的基本概念二、数轴:规定了原点、正方向和单位长度的直线.1)在数轴上表示的两个数,右边的数总比左边
的数大;2)正数都大于0,负数都小于0;正数大于一切
负数;3)所有有理数都可以用数轴上的点表示。实数3、用作图的方法在数轴上找出表示的点B数是_,
体现了________的思想方法.1、如图,数轴上A,B两点所表示
的两数的( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数O2、实数a,b,c,d在数轴上的对应点如图所示,
则它们从小到大的顺序是 。c a+b=0. (a是任意一个实数);二、实数的基本概念在数轴上表示相反数的两点以_____对称。原点1、下列各组数中,互为相反数的是( )2、若|a-3|-3+a=0,则a的取值范围是( )
A.a≥3 B.a<3 C.a≤3 D.a>34、两个相反数在数轴上的对应点在 的两
左右两侧且与 的距离相等。原点原点3、 的相反数是 ( )
A.-3 B. -1/3 C. 3 D. (2004广东) A5、-(-4)的相反数是 ,
︱- 8︳是 的相反数 cc-4-8⑴a、b互为倒数 <====> ab=1
⑵ a、b互为负倒数 <====> ab=-1零没有倒数 二、实数的基本概念四、倒数:乘积是1的两个数互为倒数 .a的倒数是 (a≠0); 4、已知a与 互为倒数,则满
足条件的实数a的个数是( )A.0 B.1 C.2 D.33、a、b互为相反数,c与d互为倒数则
a+1+b+cd= 。22、倒数是它本身的数是_______。1、若2x-3与-1/3互为倒数, 则x=___01或-1c五、绝对值:1)一个正数的绝对值是它
本身,一个负数的绝对
值是它的相反数,零
的绝对值是零。一个数a的绝对值就是数轴上
表示数a的点与原点的距离。2) 对任何实数a,总有︱a︱≥0.去绝对值的规律:体现了绝对值的结果具有非负性五、绝对值:去绝对值的规律:注意:绝对值的化简,应先判断符号内的数或式子的值是正、负、或0,然后再根据定义把绝对值的符号去掉。1、已知数轴上的A点所表示的数是2,那么在数
轴上到A点的距离是3的点所表示的数有()
A.1个 B.2个 C.3个 D.4个2、若x的相反数是3,∣y∣=5,则x+y的值为 .绝对值的性质——要注意正确区分数的三种情况,尤其是负数去掉绝对值应变为其相反数。3、若3,m,5为三角形三边,化简: B-8或22m-105、已知实数a、b、c在数轴上的位置如图,
化简 的结果是( )
A.a+c B.-a-2b+c
C.a+2b-c D. -a-cA六、近似数与有效数字: 1、 一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。 这时,从左边第一个非0数字起,到精确的数位止,所有的数字,都叫做这个数的有效数字。(特殊:科学记数法表示的数,带单位的数)2、近似数2.05与2.0500的区别。有效数字的个数精确度六、近似数与有效数字:3、精确度整数
整数带单位的数
小数带单位的数
小数
科学记数法表示的数个位带什么单位就叫精确到哪一位。一位小数消掉一个最高位。分位还原后数到的末位为止。求近似值的一种特殊方法:(1)、当把一个实数精确到十位、百位、千位、万位等时,先用科学记数法表示,再根据指定的精确度四舍五入取近似值。(2)、保留的有效数字的个数比准确数的整数部分的位数少时也如此。例如:用科学记数法表示下列各数并要求保留
两位有效数字: (1) 12033.4 (2)0.0000102练习 下列各数是由四舍五入得到的近似数,其中判断正确有( )个。① 43.8精确到个位,有三个有效数字
② 0.03068精确到十万分位,有三个有效数字
③ 0.8514精确到千分位,有四个有效数字
④ 2.4万精确到千位,有两个有效数字
⑤ 2.30×104精确到百分位,有三个有效数字A、0 B、1 C、 2 D、3 注意:
找精确度时,应把科学记数法恢复原数。近似数0.030万精确到____位,有___个有效数字,用科学记数法表示,记作____万。返回 把一个数记成 的形
式,其中 ,n 为整数。
这种记数方法叫做科学记数法。当|原数|≥1时,n等于原数的整数位数减1;当|原数|<1时,n是负整数,它的值等于原数中左起第一个数字前零的个数(包括整数位上的0).例如:用科学记数法表示下列各数: 七、科学记数法:(1) 12033.4 (2)0.0000102八、方根的有关概念:1、平方根:(定义)如果 ( ),那么x叫做a的
平方根(二次方根),记作 ,其中
叫做 a 的算术平方根。正数有_____平方根,_____________;
零的平方根是零(一个);
负数_____平方根。两个它们互为相反数没有在应用平方根定义时,一定不要忘记这一条件。(性质)算术平方根的结果是个非负数。一般地,求一个数的平方根的方法有两种:1.根据乘方意义求平方根; 2.用计算器求平方根. 1、4的平方根是 ;算术平方根是_____2、 的平方根是__,3-2的算术平方根是____.考题:±223、1.6的平方根是 ; 的算术平方根是 ;4、八、方根的有关概念:2、立方根: 正数有______的立方根;零的立方根是零;负数有______的立方根。(1)平方根是本身的数是 。
(2)算术平方根是本身的数是 。
(3)立方根是本身的数是 。(性质)一个正一个负1、64的立方根等于_____。
2、 的相反数是_____.3、如图,在数轴上,用点A大致表示 。4、已知(a-3)2+︱b-4︱=0,则a/b的平方
根是______。5、已知某个正数的平方根分别是(2x-3)和(x-3),而数a在数轴上对应点的位置在数x与-1之间,请化简式子:42返回九、有关实数的非负性: 1、若求 的值。解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-4/3,b=3/4
∴a2009b2010=(-4/3)2009·(3/4)2010=-3/41、已知 ,则实数
的相反数是 。 2、x、y是实数, +y2-6y+9=0,
若axy-3x=y,则实数a的值是 ( )
A.1/4 B.-1/4
C.7/4 D.-7/43: 若 与 互为相反数,
则 的值为 。-1A小结: ⑴要注意绝对值概念的正确应用。因为互为相反数的绝对值相等,因此绝对值等于一个正数的数有两个,它们是一对互为相反数,不可漏掉其中任何一个。 ⑵解涉及有理数的绝对值、大小比较等问题时,数轴是一个十分有效的工具。可由已知条件确定对应于数轴上的点,按“表示在数轴上的点的数,左边的数总比左边的大”进行比较大小;有时也可采用特殊值法进行判断。⑶注意平方根与算术平方根的区别与关系。要求一个数的平方根或算术平方根,须将这个数先进行化简或计算。方法小结:⑷相反数和倒数是两个重要的概念,要注意两者的区别。 (5)要注意有效数字和精确度的问题.再见
一、实数的分类
二、有理数的有关概念
1、负数
2、数轴
3、相反数
4、倒数
5、绝对值
6、近似数和有效数字
7、科学记数法
8、方根
9、三种重要的非负性
三.实数
1、有关平方根和立方根
2、实数的运算3、实数的比较大小
4、数字规律探究
5、零指数,负整指数按定义分:要点、考点聚焦按正负分:一、实数的分类:实数有理数整数正整数(自然数)零负整数分数正分数负分数无理数正无理数负无理数负无理数负分数负整数负有理数负实数零正无理数正分数正整数正有理数正实数实数(自然数)返回考题: 1、写出一个无理数,使它与 的积是有理
数:________c3无限不循环小数叫做无理数
( 强调: 无限 、 不循环.)
无理数常见的4种典型:注意:(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)(4)、三角函数型:tan60°,sin45 °... 返回二、实数的基本概念一.负数:在正数前面加“—”的数;0既不是正数,也不是负数。1、判断:
1)a一定是正数; ( )
2)-a一定是负数; ( )
3)-(-a)一定大于0; ( )
4)0是正整数。 ( )××××2、(1)如果零上5℃记作5℃,则零下2℃记作_____
(2) 如果上升10m记作10m,那么-5m表示____
(3)比海平面低35m的地方,它的高度是海拔___ 数轴上的点与_____是一一对应的。二、实数的基本概念二、数轴:规定了原点、正方向和单位长度的直线.1)在数轴上表示的两个数,右边的数总比左边
的数大;2)正数都大于0,负数都小于0;正数大于一切
负数;3)所有有理数都可以用数轴上的点表示。实数3、用作图的方法在数轴上找出表示的点B数是_,
体现了________的思想方法.1、如图,数轴上A,B两点所表示
的两数的( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数O2、实数a,b,c,d在数轴上的对应点如图所示,
则它们从小到大的顺序是 。c
A.a≥3 B.a<3 C.a≤3 D.a>34、两个相反数在数轴上的对应点在 的两
左右两侧且与 的距离相等。原点原点3、 的相反数是 ( )
A.-3 B. -1/3 C. 3 D. (2004广东) A5、-(-4)的相反数是 ,
︱- 8︳是 的相反数 cc-4-8⑴a、b互为倒数 <====> ab=1
⑵ a、b互为负倒数 <====> ab=-1零没有倒数 二、实数的基本概念四、倒数:乘积是1的两个数互为倒数 .a的倒数是 (a≠0); 4、已知a与 互为倒数,则满
足条件的实数a的个数是( )A.0 B.1 C.2 D.33、a、b互为相反数,c与d互为倒数则
a+1+b+cd= 。22、倒数是它本身的数是_______。1、若2x-3与-1/3互为倒数, 则x=___01或-1c五、绝对值:1)一个正数的绝对值是它
本身,一个负数的绝对
值是它的相反数,零
的绝对值是零。一个数a的绝对值就是数轴上
表示数a的点与原点的距离。2) 对任何实数a,总有︱a︱≥0.去绝对值的规律:体现了绝对值的结果具有非负性五、绝对值:去绝对值的规律:注意:绝对值的化简,应先判断符号内的数或式子的值是正、负、或0,然后再根据定义把绝对值的符号去掉。1、已知数轴上的A点所表示的数是2,那么在数
轴上到A点的距离是3的点所表示的数有()
A.1个 B.2个 C.3个 D.4个2、若x的相反数是3,∣y∣=5,则x+y的值为 .绝对值的性质——要注意正确区分数的三种情况,尤其是负数去掉绝对值应变为其相反数。3、若3,m,5为三角形三边,化简: B-8或22m-105、已知实数a、b、c在数轴上的位置如图,
化简 的结果是( )
A.a+c B.-a-2b+c
C.a+2b-c D. -a-cA六、近似数与有效数字: 1、 一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。 这时,从左边第一个非0数字起,到精确的数位止,所有的数字,都叫做这个数的有效数字。(特殊:科学记数法表示的数,带单位的数)2、近似数2.05与2.0500的区别。有效数字的个数精确度六、近似数与有效数字:3、精确度整数
整数带单位的数
小数带单位的数
小数
科学记数法表示的数个位带什么单位就叫精确到哪一位。一位小数消掉一个最高位。分位还原后数到的末位为止。求近似值的一种特殊方法:(1)、当把一个实数精确到十位、百位、千位、万位等时,先用科学记数法表示,再根据指定的精确度四舍五入取近似值。(2)、保留的有效数字的个数比准确数的整数部分的位数少时也如此。例如:用科学记数法表示下列各数并要求保留
两位有效数字: (1) 12033.4 (2)0.0000102练习 下列各数是由四舍五入得到的近似数,其中判断正确有( )个。① 43.8精确到个位,有三个有效数字
② 0.03068精确到十万分位,有三个有效数字
③ 0.8514精确到千分位,有四个有效数字
④ 2.4万精确到千位,有两个有效数字
⑤ 2.30×104精确到百分位,有三个有效数字A、0 B、1 C、 2 D、3 注意:
找精确度时,应把科学记数法恢复原数。近似数0.030万精确到____位,有___个有效数字,用科学记数法表示,记作____万。返回 把一个数记成 的形
式,其中 ,n 为整数。
这种记数方法叫做科学记数法。当|原数|≥1时,n等于原数的整数位数减1;当|原数|<1时,n是负整数,它的值等于原数中左起第一个数字前零的个数(包括整数位上的0).例如:用科学记数法表示下列各数: 七、科学记数法:(1) 12033.4 (2)0.0000102八、方根的有关概念:1、平方根:(定义)如果 ( ),那么x叫做a的
平方根(二次方根),记作 ,其中
叫做 a 的算术平方根。正数有_____平方根,_____________;
零的平方根是零(一个);
负数_____平方根。两个它们互为相反数没有在应用平方根定义时,一定不要忘记这一条件。(性质)算术平方根的结果是个非负数。一般地,求一个数的平方根的方法有两种:1.根据乘方意义求平方根; 2.用计算器求平方根. 1、4的平方根是 ;算术平方根是_____2、 的平方根是__,3-2的算术平方根是____.考题:±223、1.6的平方根是 ; 的算术平方根是 ;4、八、方根的有关概念:2、立方根: 正数有______的立方根;零的立方根是零;负数有______的立方根。(1)平方根是本身的数是 。
(2)算术平方根是本身的数是 。
(3)立方根是本身的数是 。(性质)一个正一个负1、64的立方根等于_____。
2、 的相反数是_____.3、如图,在数轴上,用点A大致表示 。4、已知(a-3)2+︱b-4︱=0,则a/b的平方
根是______。5、已知某个正数的平方根分别是(2x-3)和(x-3),而数a在数轴上对应点的位置在数x与-1之间,请化简式子:42返回九、有关实数的非负性: 1、若求 的值。解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-4/3,b=3/4
∴a2009b2010=(-4/3)2009·(3/4)2010=-3/41、已知 ,则实数
的相反数是 。 2、x、y是实数, +y2-6y+9=0,
若axy-3x=y,则实数a的值是 ( )
A.1/4 B.-1/4
C.7/4 D.-7/43: 若 与 互为相反数,
则 的值为 。-1A小结: ⑴要注意绝对值概念的正确应用。因为互为相反数的绝对值相等,因此绝对值等于一个正数的数有两个,它们是一对互为相反数,不可漏掉其中任何一个。 ⑵解涉及有理数的绝对值、大小比较等问题时,数轴是一个十分有效的工具。可由已知条件确定对应于数轴上的点,按“表示在数轴上的点的数,左边的数总比左边的大”进行比较大小;有时也可采用特殊值法进行判断。⑶注意平方根与算术平方根的区别与关系。要求一个数的平方根或算术平方根,须将这个数先进行化简或计算。方法小结:⑷相反数和倒数是两个重要的概念,要注意两者的区别。 (5)要注意有效数字和精确度的问题.再见
同课章节目录
