九年级数学上册 25.2 解直角三角形教案 沪教版五四制
文档属性
| 名称 | 九年级数学上册 25.2 解直角三角形教案 沪教版五四制 |

|
|
| 格式 | zip | ||
| 文件大小 | 106.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-15 21:47:31 | ||
图片预览



文档简介
解直角三角形
教学目标
1、掌握解直角三角形,并能根据题意把实际问题中的已知条件和未知元素,化归到某个直角三角形中加以解决。会把实际问题转化为含有直角三角形的数学问题,并能给予解决。2、通过问题探究和解决,丰富对现实空间及图形的认识,培养分析、归纳、总结知识的能力。3、体验数学与生活实际的密切关联,进一步激发学生学习数学的兴趣,逐步养成良好的学习品质。
重点、难点
重点:把实际问题中的已知条件和未知元素,化归到某个直角三角形中加以解决。难点:把实际问题转化为解直角三角形的数学问题
教学内容
1.1~1.2锐角三角函数及其计算边角之间的关系(锐角三角函数):★
★
三角函数的单调性:如下图,⊙是一个单位圆,假设其半径为1,则对于,,,其它均可用上图来证明。
( http: / / www.21cnjy.com )30°,45°,60°的三角函数值(见右表)例(1)计算:
sin60°·tan30°+cos
45°=(2)把Rt△ABC各边的长度都扩大3倍得Rt△A’B’C’,那么锐角A、A’的余弦值的关系为
(3)在△ABC中,∠C=90°,tanA=,则sinB=
,cosB=
(4)如果那么△ABC是
(5)在的对边,已知,则的值等于
(6)已知cosα<0.5,那么锐角α的取值范围是
(7)已知α为锐角,则m=sinα+cosα的值(
)
A.m>1
B.m=1
C.m<1
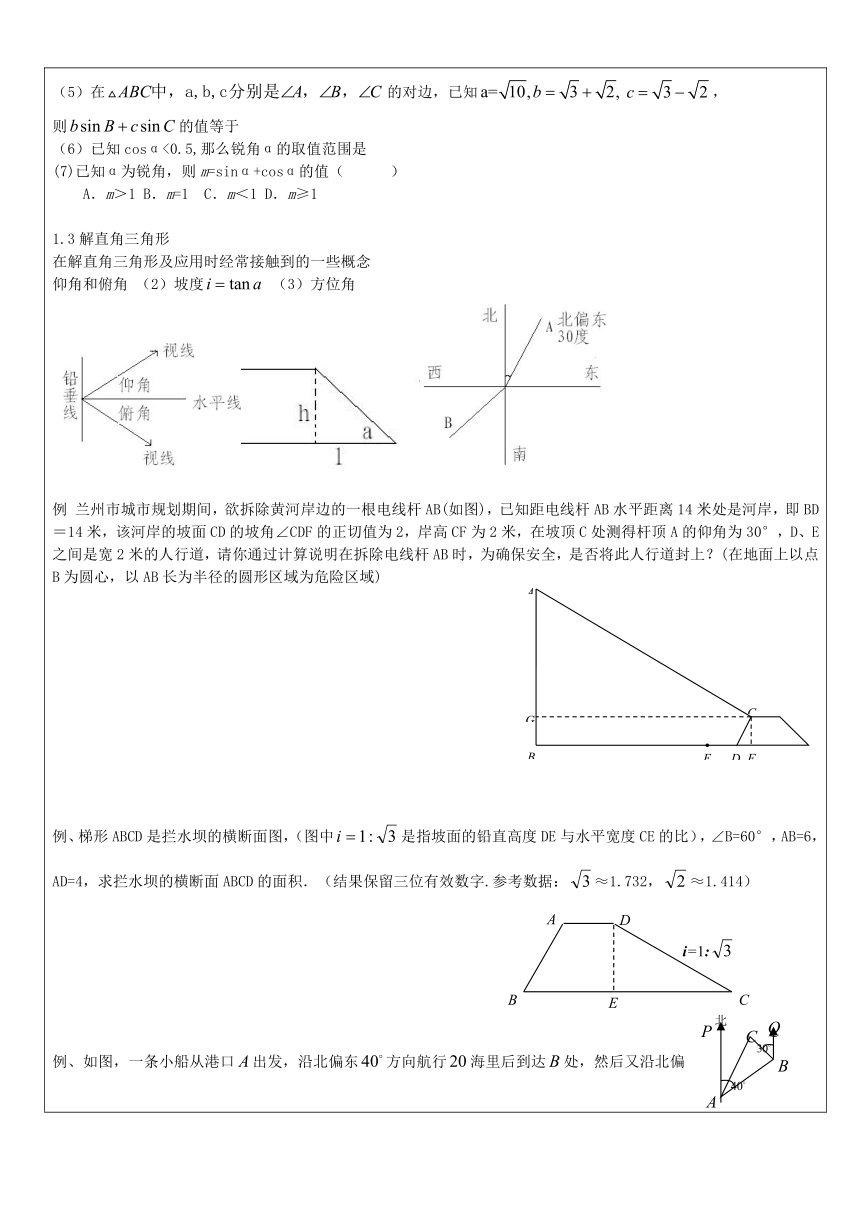
D.m≥11.3解直角三角形在解直角三角形及应用时经常接触到的一些概念仰角和俯角
(2)坡度
(3)方位角
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )例
兰州市城市规划期间,欲拆除黄河岸边的
( http: / / www.21cnjy.com )一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)例、梯形ABCD是拦水坝的横断面图,(图中是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:≈1.732,≈1.414)例、如图,一条小船从港口出发,沿北偏东方向航行海里后到达处,然后又沿北偏西方向航行海里后到达处.问此时小船距港口多少海里?(结果精确到1海里),,,.例、如图所示,A、B两地之间有一条河,原来从A地到B地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.一直BC=11km,∠A=45°,∠B=37°.桥DC和AB平行,则现在从A地到达B地可比原来少走多少路程?(结果精确到0.1km.参考数据:,sin37°≈0.60,cos37°≈0.80)例、由于过度采伐森林和破坏植被,我国部分地
( http: / / www.21cnjy.com )区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?【经典习题】1.雄伟壮观的“千年塔”屹立在海口市西海岸带状公园的“热带海洋世界”.在一次数学实践活动中,为了测量这座“千年塔”的高度,雯雯在离塔底139米的C处(C与塔底B在同一水平线上),用高1.4米的测角仪CD测得塔项A的仰角α=43°(如图),求这座“千年塔”的高度AB(结果精确到0.1米).(参考数据:tan43°≈0.9325,
cot43°≈1.0724)2.如图,一渔船以32千米/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东300,半小时后航行到B处看到灯塔S在船的北偏东750,若渔船继续向正北航行到C处时,灯塔S和船的距离最短,求灯塔S与C的距离。(计算过程和结果一律不取近似值)3.如图,已知两座高度相等的建筑物AB、CD的水平距离BC=60米,在建筑物CD上有一铁塔PD,在塔顶P处观察建筑物的底部B和顶部A,分别测行俯角,求建筑物AB的高。(计算过程和结果一律不取近似值)4.如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14米到达D,在D处测得A的仰角为45°,求铁塔AB的高。5.下图为住宅区内的两幢楼,它们的高,现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求:1)若两楼间的距离时,甲楼的影子,落在乙楼上有多高?2)若甲楼的影子,刚好不影响乙楼,那么两楼的距离应当有多远?6.如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10千米的速度向北偏东60 的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域。问A城是否会受到这次台风的影响?为什么?若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?初三数学
解直角三角形的应用一、选择题:1.已知等腰三角形底边上的高等于腰的,则项角为
(
)
(A)
300
(B)
450
(C)
600
(D)
9002.菱形ABCD的对角线AC=10,BD=6,则
tan=
(
)
(A)
(B)
(C)
(D)以上都不对3.在高出海平面100米的山岩上一点A,看
( http: / / www.21cnjy.com )到一艘船B的俯角为300,则船与山脚的水平距离为
(
)
(A)
50米
(B)200米
(C)100米
(D)米4.正方形的对角线长为,则正方形的面积为
(
)
(A)
9
(B)
(C)
(D)5.如果三角形的斜边长为4,一条直角边长为2,那么斜边的高为
(
)
(A)
2
(B)
(C)
(D)26.Rt△ABC中,∠C=900,斜边AB的坡度为1:2,若BCAC,则BC:AC:BA等于
(
)
(A)
1:2:(B)1::2
(C)
1:
(D)1:2:57.若从山项A望地面C、D
( http: / / www.21cnjy.com )两点的俯角分别为450、300,C、D与山脚B共线,若CD=100米,那么山高AB为
(
)
(A)
100米
(B)
50米
(C)
50米
(D)
50()米8.已知△ABC中,AD是高,AD=2,DB=2,CD=2,则∠BAC=
(
)
(A)
1050
(B)
150
(C)
1050或150
(D)
6009.已知△ABC中,∠ABC=900,∠ACB=450,D在BC的延长线上,且CD=CA,则cot的值为
(
)
(A)
(B)
(C)
(D)10.已知:△ABC中,∠BCA=900,CD⊥AB于D,若AD=1,AB=3,那么∠B的余弦值为(
)
(A)
(B)
(C)
(D)二、填空题:1.若地面上的甲看到高山上乙的仰角为200,则乙看到甲的俯角为
度。2.已知一斜坡的坡度为1:,则斜坡的坡度为
。3.已知一斜坡的坡度为1:4,水平距离为20米,则该斜坡的垂直高度为
。4.在山坡上种树,要求株距为5.5米,测得斜坡的倾斜角为300,则斜坡上的相邻两株间的坡面距离是
米。5.已知直角梯形ABCD中,AB∥CD,∠D=900,AC⊥BC,若AC=3,BC=3,则AB=
。6.已知锐角△ABC中,AD⊥BC于D,∠B=450,DC=1,且=3,则AB=
。7.已知菱形的两条对角线分别是8和8,则菱形的周长为
。已知如图,将两根宽度为2cm的纸带交叉叠放,若∠α为已知,则阴影部分面积为
。如图所示,某建筑物BC直立于水平地面,AC=9米,要建造阶梯AB,使每阶高不超过20厘米,则阶梯至少要建
阶。(最后一阶的高不足20厘米时,按一阶计算;取1.732)三、解答题:已知如图,Rt△ABC中,∠ACB=900,D是AB的中点,sinα=,AC=,求
。2.已知如图:四边形ABCD中,∠B=∠D=900,∠BAD=600,且BC=11,CD=2,求AC的长。3.我人民解放军在进行“解放一号”军事
( http: / / www.21cnjy.com )演习时,于海拔高度为600米的某海岛顶端A处设立了一个观察点(如图)上午九时,观察员发现“红方C舰”和“蓝方D舰”与该岛恰好在一条直线上,并测得“红方C舰”的俯角为300,测得“蓝方D舰”的俯角为80,请求出这时两舰之间的距离。(参考数据:)4.如图所示,一勘测人员从B出发,
( http: / / www.21cnjy.com )沿坡度为150的坡面以5千米/时的速度行至D点,用了12分钟,然后沿坡度为200的坡面以3千米/时行至山顶A处,用了10分钟,求山高(即AC的长度)及A、B两点的水平距离。(即BC的长度)(精确到0.01千米)(sin150=0.2588
,
cos150=0.9659
,
sin200=0.3420
,
cos200=0.9397)5.在生活中需要测量一些球(如足球、篮球……)的直径,某校研究学习小组,通过实验发现下面的测量方法:如图所示,将球放在水平的桌面上,在阳光的斜射下,得到球的影子AB,设光线DA、CB分别与球相切于点E、F,则EF即为球的直径,若测得AB的长为41.5cm,∠ABC=370,请你计算出球的直径(精确到1cm)。
6.某村计划开挖一条长1500米的水渠,渠道的断面为等腰梯形,渠道深0.8米,下底宽1.2米,坡角为450(如图所示)。实际开发渠道时,每天比原计划多挖20立方米,结果比原计划提前4天完成,求原计划每天挖土多少立方米。7.在半径为27m的圆形广场中央点O上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为1200(如图所示),求光源离地面的垂直高度SO(精确到0.1m)。(,以上数据供参考)
C
B
A
D
E
F
G
A
D
B
E
i=1:
C
A
B
C
D
α
A
C
D
B
甲
乙
A
C
300
B
D
F
E
D
C
A
教学目标
1、掌握解直角三角形,并能根据题意把实际问题中的已知条件和未知元素,化归到某个直角三角形中加以解决。会把实际问题转化为含有直角三角形的数学问题,并能给予解决。2、通过问题探究和解决,丰富对现实空间及图形的认识,培养分析、归纳、总结知识的能力。3、体验数学与生活实际的密切关联,进一步激发学生学习数学的兴趣,逐步养成良好的学习品质。
重点、难点
重点:把实际问题中的已知条件和未知元素,化归到某个直角三角形中加以解决。难点:把实际问题转化为解直角三角形的数学问题
教学内容
1.1~1.2锐角三角函数及其计算边角之间的关系(锐角三角函数):★
★
三角函数的单调性:如下图,⊙是一个单位圆,假设其半径为1,则对于,,,其它均可用上图来证明。
( http: / / www.21cnjy.com )30°,45°,60°的三角函数值(见右表)例(1)计算:
sin60°·tan30°+cos
45°=(2)把Rt△ABC各边的长度都扩大3倍得Rt△A’B’C’,那么锐角A、A’的余弦值的关系为
(3)在△ABC中,∠C=90°,tanA=,则sinB=
,cosB=
(4)如果那么△ABC是
(5)在的对边,已知,则的值等于
(6)已知cosα<0.5,那么锐角α的取值范围是
(7)已知α为锐角,则m=sinα+cosα的值(
)
A.m>1
B.m=1
C.m<1
D.m≥11.3解直角三角形在解直角三角形及应用时经常接触到的一些概念仰角和俯角
(2)坡度
(3)方位角
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )例
兰州市城市规划期间,欲拆除黄河岸边的
( http: / / www.21cnjy.com )一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)例、梯形ABCD是拦水坝的横断面图,(图中是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:≈1.732,≈1.414)例、如图,一条小船从港口出发,沿北偏东方向航行海里后到达处,然后又沿北偏西方向航行海里后到达处.问此时小船距港口多少海里?(结果精确到1海里),,,.例、如图所示,A、B两地之间有一条河,原来从A地到B地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.一直BC=11km,∠A=45°,∠B=37°.桥DC和AB平行,则现在从A地到达B地可比原来少走多少路程?(结果精确到0.1km.参考数据:,sin37°≈0.60,cos37°≈0.80)例、由于过度采伐森林和破坏植被,我国部分地
( http: / / www.21cnjy.com )区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?【经典习题】1.雄伟壮观的“千年塔”屹立在海口市西海岸带状公园的“热带海洋世界”.在一次数学实践活动中,为了测量这座“千年塔”的高度,雯雯在离塔底139米的C处(C与塔底B在同一水平线上),用高1.4米的测角仪CD测得塔项A的仰角α=43°(如图),求这座“千年塔”的高度AB(结果精确到0.1米).(参考数据:tan43°≈0.9325,
cot43°≈1.0724)2.如图,一渔船以32千米/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东300,半小时后航行到B处看到灯塔S在船的北偏东750,若渔船继续向正北航行到C处时,灯塔S和船的距离最短,求灯塔S与C的距离。(计算过程和结果一律不取近似值)3.如图,已知两座高度相等的建筑物AB、CD的水平距离BC=60米,在建筑物CD上有一铁塔PD,在塔顶P处观察建筑物的底部B和顶部A,分别测行俯角,求建筑物AB的高。(计算过程和结果一律不取近似值)4.如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14米到达D,在D处测得A的仰角为45°,求铁塔AB的高。5.下图为住宅区内的两幢楼,它们的高,现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求:1)若两楼间的距离时,甲楼的影子,落在乙楼上有多高?2)若甲楼的影子,刚好不影响乙楼,那么两楼的距离应当有多远?6.如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10千米的速度向北偏东60 的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域。问A城是否会受到这次台风的影响?为什么?若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?初三数学
解直角三角形的应用一、选择题:1.已知等腰三角形底边上的高等于腰的,则项角为
(
)
(A)
300
(B)
450
(C)
600
(D)
9002.菱形ABCD的对角线AC=10,BD=6,则
tan=
(
)
(A)
(B)
(C)
(D)以上都不对3.在高出海平面100米的山岩上一点A,看
( http: / / www.21cnjy.com )到一艘船B的俯角为300,则船与山脚的水平距离为
(
)
(A)
50米
(B)200米
(C)100米
(D)米4.正方形的对角线长为,则正方形的面积为
(
)
(A)
9
(B)
(C)
(D)5.如果三角形的斜边长为4,一条直角边长为2,那么斜边的高为
(
)
(A)
2
(B)
(C)
(D)26.Rt△ABC中,∠C=900,斜边AB的坡度为1:2,若BCAC,则BC:AC:BA等于
(
)
(A)
1:2:(B)1::2
(C)
1:
(D)1:2:57.若从山项A望地面C、D
( http: / / www.21cnjy.com )两点的俯角分别为450、300,C、D与山脚B共线,若CD=100米,那么山高AB为
(
)
(A)
100米
(B)
50米
(C)
50米
(D)
50()米8.已知△ABC中,AD是高,AD=2,DB=2,CD=2,则∠BAC=
(
)
(A)
1050
(B)
150
(C)
1050或150
(D)
6009.已知△ABC中,∠ABC=900,∠ACB=450,D在BC的延长线上,且CD=CA,则cot的值为
(
)
(A)
(B)
(C)
(D)10.已知:△ABC中,∠BCA=900,CD⊥AB于D,若AD=1,AB=3,那么∠B的余弦值为(
)
(A)
(B)
(C)
(D)二、填空题:1.若地面上的甲看到高山上乙的仰角为200,则乙看到甲的俯角为
度。2.已知一斜坡的坡度为1:,则斜坡的坡度为
。3.已知一斜坡的坡度为1:4,水平距离为20米,则该斜坡的垂直高度为
。4.在山坡上种树,要求株距为5.5米,测得斜坡的倾斜角为300,则斜坡上的相邻两株间的坡面距离是
米。5.已知直角梯形ABCD中,AB∥CD,∠D=900,AC⊥BC,若AC=3,BC=3,则AB=
。6.已知锐角△ABC中,AD⊥BC于D,∠B=450,DC=1,且=3,则AB=
。7.已知菱形的两条对角线分别是8和8,则菱形的周长为
。已知如图,将两根宽度为2cm的纸带交叉叠放,若∠α为已知,则阴影部分面积为
。如图所示,某建筑物BC直立于水平地面,AC=9米,要建造阶梯AB,使每阶高不超过20厘米,则阶梯至少要建
阶。(最后一阶的高不足20厘米时,按一阶计算;取1.732)三、解答题:已知如图,Rt△ABC中,∠ACB=900,D是AB的中点,sinα=,AC=,求
。2.已知如图:四边形ABCD中,∠B=∠D=900,∠BAD=600,且BC=11,CD=2,求AC的长。3.我人民解放军在进行“解放一号”军事
( http: / / www.21cnjy.com )演习时,于海拔高度为600米的某海岛顶端A处设立了一个观察点(如图)上午九时,观察员发现“红方C舰”和“蓝方D舰”与该岛恰好在一条直线上,并测得“红方C舰”的俯角为300,测得“蓝方D舰”的俯角为80,请求出这时两舰之间的距离。(参考数据:)4.如图所示,一勘测人员从B出发,
( http: / / www.21cnjy.com )沿坡度为150的坡面以5千米/时的速度行至D点,用了12分钟,然后沿坡度为200的坡面以3千米/时行至山顶A处,用了10分钟,求山高(即AC的长度)及A、B两点的水平距离。(即BC的长度)(精确到0.01千米)(sin150=0.2588
,
cos150=0.9659
,
sin200=0.3420
,
cos200=0.9397)5.在生活中需要测量一些球(如足球、篮球……)的直径,某校研究学习小组,通过实验发现下面的测量方法:如图所示,将球放在水平的桌面上,在阳光的斜射下,得到球的影子AB,设光线DA、CB分别与球相切于点E、F,则EF即为球的直径,若测得AB的长为41.5cm,∠ABC=370,请你计算出球的直径(精确到1cm)。
6.某村计划开挖一条长1500米的水渠,渠道的断面为等腰梯形,渠道深0.8米,下底宽1.2米,坡角为450(如图所示)。实际开发渠道时,每天比原计划多挖20立方米,结果比原计划提前4天完成,求原计划每天挖土多少立方米。7.在半径为27m的圆形广场中央点O上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为1200(如图所示),求光源离地面的垂直高度SO(精确到0.1m)。(,以上数据供参考)
C
B
A
D
E
F
G
A
D
B
E
i=1:
C
A
B
C
D
α
A
C
D
B
甲
乙
A
C
300
B
D
F
E
D
C
A
