九年级数学上册 25.2 求锐角的三角比的值教案 沪教版五四制
文档属性
| 名称 | 九年级数学上册 25.2 求锐角的三角比的值教案 沪教版五四制 |
|
|
| 格式 | zip | ||
| 文件大小 | 202.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-15 21:50:43 | ||
图片预览


文档简介
锐角三角比
教学目标
考查学生的做题习惯与做题方法培养学生做笔记的习惯与学会简单方法
重点、难点
知识点的应用与总结,学生做题方法的训练
考点及考试要求
知识点的灵活应用
教学内容
锐角三角比:知识点一:锐角三角比的定义:锐角三角比定义:在Rt△ABC中,∠C=900,
∠A、∠B、∠C的对边分别为a、b、c,则∠A的正弦可表示为:sinA=
,
∠A的余弦可表示为cosA=
∠A的正切:tanA=
,它们弦称为∠A的锐角三角比2、取值范围
cosA<
tanA>
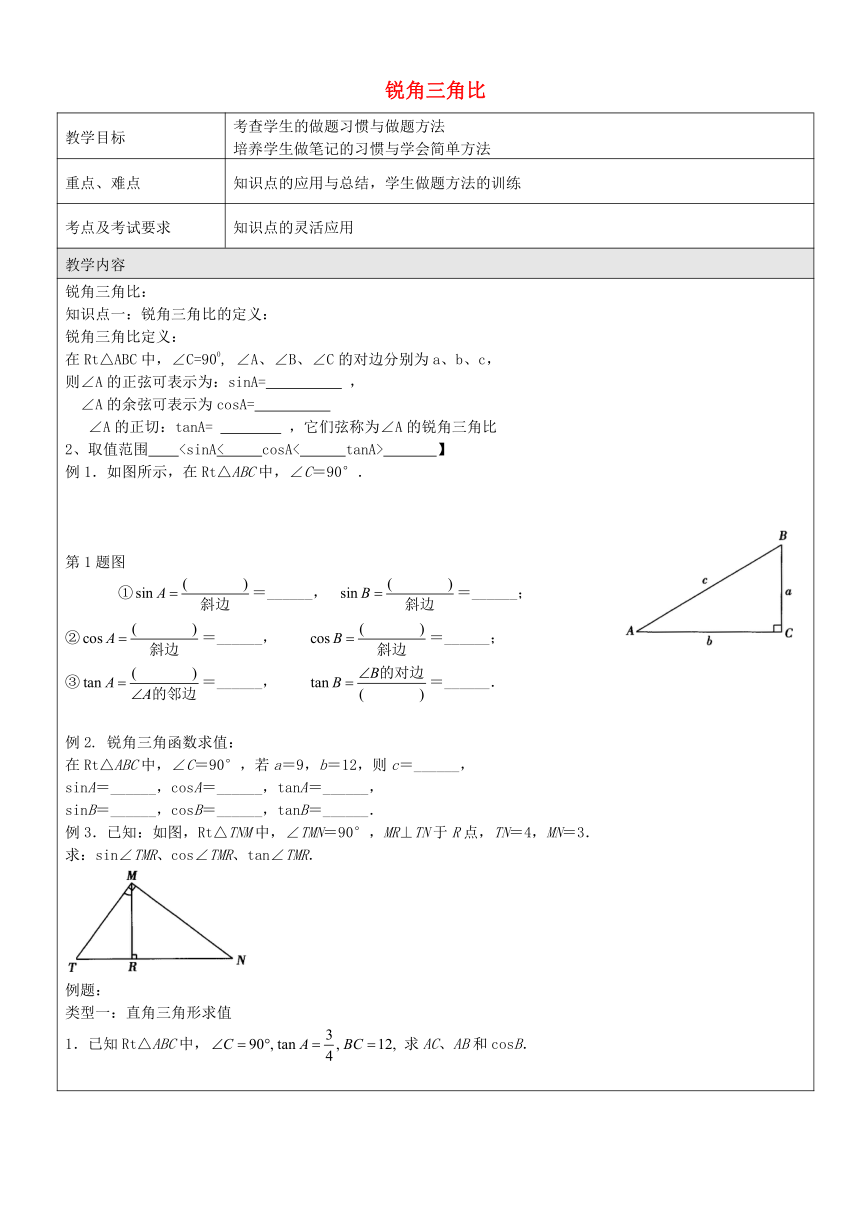
】例1.如图所示,在Rt△ABC中,∠C=90°.
第1题图
①=______,
=______;②=______,
=______;③=______,
=______.例2.
锐角三角函数求值:在Rt△ABC中,∠C=90°,若a=9,b=12,则c=______,sinA=______,cosA=______,tanA=______,sinB=______,cosB=______,tanB=______.例3.已知:如图,Rt△TNM中,∠TMN=90°,MR⊥TN于R点,TN=4,MN=3.求:sin∠TMR、cos∠TMR、tan∠TMR.
( http: / / www.21cnjy.com )例题:类型一:直角三角形求值1.已知Rt△ABC中,求AC、AB和cosB.2.如图,⊙O的半径OA=16cm,OC⊥AB于C点,求AB及OC的长.
( http: / / www.21cnjy.com )3.已知:⊙O中,OC⊥AB于C点,AB=16cm,(1)求⊙O的半径OA的长及弦心距OC;(2)求cos∠AOC及tan∠AOC.已知是锐角,,求,的值针对训练:1.在Rt△ABC中,∠
C=90°,若BC=1,AB=,则tanA的值为A.
B.
C.
D.2
2.在△ABC中,∠C=90°,sinA=,那么tanA的值等于(
).A.
B.
C.
D.
类型二.
利用角度转化求值:1.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点.DE∶AE=1∶2.求:sinB、cosB、tanB.
( http: / / www.21cnjy.com )2.
如图,直径为10的⊙A经过点和点,与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为(
)A.
B.
C.
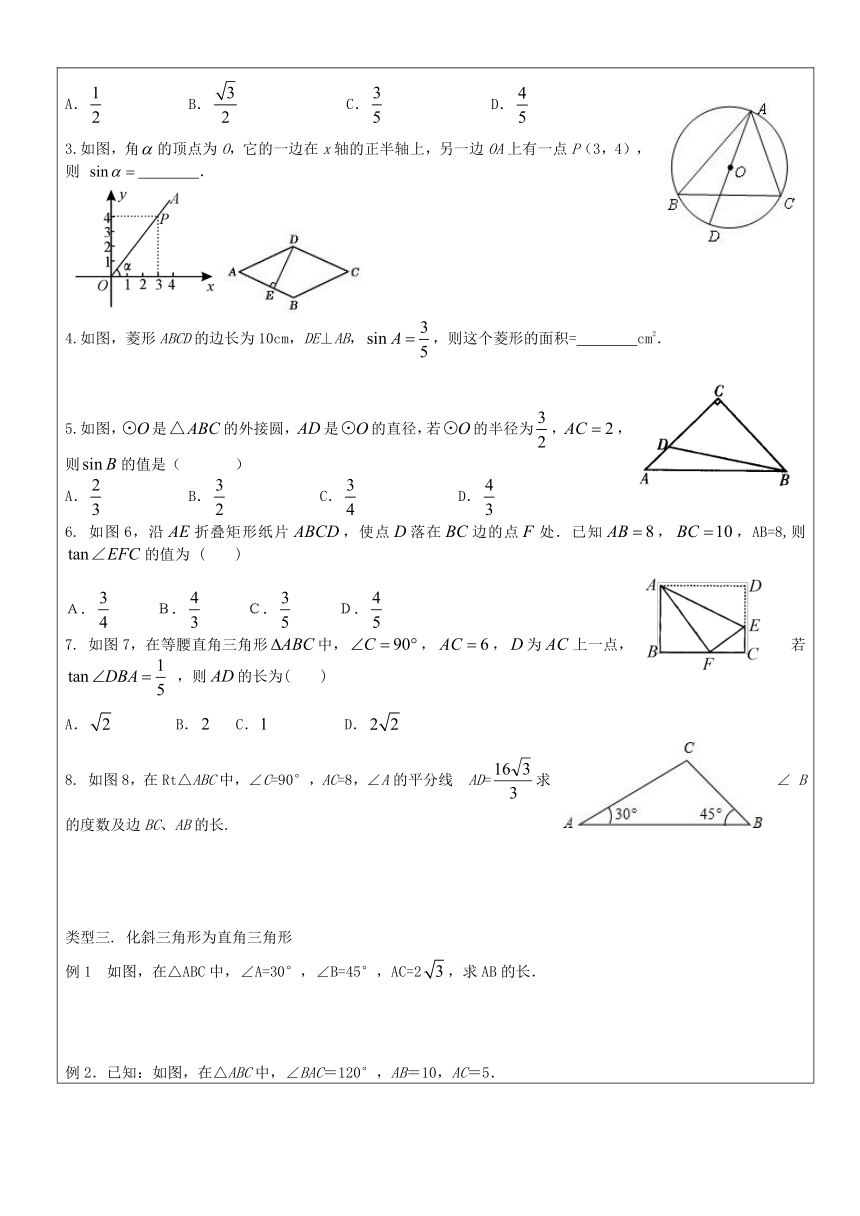
D.3.如图,角的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则
.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )4.如图,菱形ABCD的边长为10cm,DE⊥AB,,则这个菱形的面积=
cm2.5.如图,是的外接圆,是的直径,若的半径为,,则的值是(
)A.
B.
C.
D.6.
如图6,沿折叠矩形纸片,使点落在边的点处.已知,,AB=8,则的值为
(
)A.
B.
C.
D.7.
如图7,在等腰直角三角形中,,,为上一点,若
,则的长为(
)A.
B.
C.
D.
8.
如图8,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线?AD=求
∠B的度数及边BC、AB的长.类型三.
化斜三角形为直角三角形例1
如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长.例2.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.针对训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
( http: / / www.21cnjy.com )2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sinB.3.
ABC中,∠A=60°,AB=6
cm,AC=4
cm,则△ABC的面积是A.2
cm2
.4
cm2
C.6
cm2
D.12
cm2类型四:利用网格构造直角三角形例1
如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )A.
B.
C.
D.对应练习:1.如图,△ABC的顶点都在方格纸的格点上,则sin
A
=_______.2.如图,A、B、C三点在正方形网络线的交点处,若将绕着点A逆时针旋转得到,则的值为A.
B.
C.
D.
3.正方形网格中,如图放置,则tan的值是(
)
A.
EQ
\F(,5)
B.
EQ
\F(2,5)
C.
D.
2
特殊角的三角函数值锐角 30°45°60°sin cos tan 当
时,正弦和正切值随着角度的增大而
余弦值随着角度的增大而
例1.求下列各式的值.1).计算:.
2)计算:.3)计算:3-1+(2π-1)0-tan30°-tan45°
4.计算:.5.计算:
;家庭作业:1.已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,求此菱形的周长.2.已知:如图,Rt△ABC中,∠C=90°,,作∠DAC=30°,AD交CB于D点,求:(1)∠BAD;(2)sin∠BAD、cos∠BAD和tan∠BAD.3.
已知:如图△ABC中,D为BC中点,且∠BAD=90°,,求:sin∠CAD、cos∠CAD、tan∠CAD.
( http: / / www.21cnjy.com )4.
如图,在Rt△ABC中,∠C=90°,,点D在BC边上,DC=
AC
=
6,求tan
∠BAD的值.5.如图,△ABC中,∠A=30°,,.求AB的长.
教学目标
考查学生的做题习惯与做题方法培养学生做笔记的习惯与学会简单方法
重点、难点
知识点的应用与总结,学生做题方法的训练
考点及考试要求
知识点的灵活应用
教学内容
锐角三角比:知识点一:锐角三角比的定义:锐角三角比定义:在Rt△ABC中,∠C=900,
∠A、∠B、∠C的对边分别为a、b、c,则∠A的正弦可表示为:sinA=
,
∠A的余弦可表示为cosA=
∠A的正切:tanA=
,它们弦称为∠A的锐角三角比2、取值范围
tanA>
】例1.如图所示,在Rt△ABC中,∠C=90°.
第1题图
①=______,
=______;②=______,
=______;③=______,
=______.例2.
锐角三角函数求值:在Rt△ABC中,∠C=90°,若a=9,b=12,则c=______,sinA=______,cosA=______,tanA=______,sinB=______,cosB=______,tanB=______.例3.已知:如图,Rt△TNM中,∠TMN=90°,MR⊥TN于R点,TN=4,MN=3.求:sin∠TMR、cos∠TMR、tan∠TMR.
( http: / / www.21cnjy.com )例题:类型一:直角三角形求值1.已知Rt△ABC中,求AC、AB和cosB.2.如图,⊙O的半径OA=16cm,OC⊥AB于C点,求AB及OC的长.
( http: / / www.21cnjy.com )3.已知:⊙O中,OC⊥AB于C点,AB=16cm,(1)求⊙O的半径OA的长及弦心距OC;(2)求cos∠AOC及tan∠AOC.已知是锐角,,求,的值针对训练:1.在Rt△ABC中,∠
C=90°,若BC=1,AB=,则tanA的值为A.
B.
C.
D.2
2.在△ABC中,∠C=90°,sinA=,那么tanA的值等于(
).A.
B.
C.
D.
类型二.
利用角度转化求值:1.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点.DE∶AE=1∶2.求:sinB、cosB、tanB.
( http: / / www.21cnjy.com )2.
如图,直径为10的⊙A经过点和点,与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为(
)A.
B.
C.
D.3.如图,角的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则
.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )4.如图,菱形ABCD的边长为10cm,DE⊥AB,,则这个菱形的面积=
cm2.5.如图,是的外接圆,是的直径,若的半径为,,则的值是(
)A.
B.
C.
D.6.
如图6,沿折叠矩形纸片,使点落在边的点处.已知,,AB=8,则的值为
(
)A.
B.
C.
D.7.
如图7,在等腰直角三角形中,,,为上一点,若
,则的长为(
)A.
B.
C.
D.
8.
如图8,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线?AD=求
∠B的度数及边BC、AB的长.类型三.
化斜三角形为直角三角形例1
如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长.例2.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.针对训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
( http: / / www.21cnjy.com )2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sinB.3.
ABC中,∠A=60°,AB=6
cm,AC=4
cm,则△ABC的面积是A.2
cm2
.4
cm2
C.6
cm2
D.12
cm2类型四:利用网格构造直角三角形例1
如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )A.
B.
C.
D.对应练习:1.如图,△ABC的顶点都在方格纸的格点上,则sin
A
=_______.2.如图,A、B、C三点在正方形网络线的交点处,若将绕着点A逆时针旋转得到,则的值为A.
B.
C.
D.
3.正方形网格中,如图放置,则tan的值是(
)
A.
EQ
\F(,5)
B.
EQ
\F(2,5)
C.
D.
2
特殊角的三角函数值锐角 30°45°60°sin cos tan 当
时,正弦和正切值随着角度的增大而
余弦值随着角度的增大而
例1.求下列各式的值.1).计算:.
2)计算:.3)计算:3-1+(2π-1)0-tan30°-tan45°
4.计算:.5.计算:
;家庭作业:1.已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,求此菱形的周长.2.已知:如图,Rt△ABC中,∠C=90°,,作∠DAC=30°,AD交CB于D点,求:(1)∠BAD;(2)sin∠BAD、cos∠BAD和tan∠BAD.3.
已知:如图△ABC中,D为BC中点,且∠BAD=90°,,求:sin∠CAD、cos∠CAD、tan∠CAD.
( http: / / www.21cnjy.com )4.
如图,在Rt△ABC中,∠C=90°,,点D在BC边上,DC=
AC
=
6,求tan
∠BAD的值.5.如图,△ABC中,∠A=30°,,.求AB的长.
