沪教版五四制八年级数学上册 19.3 勾股定理教案(表格式)
文档属性
| 名称 | 沪教版五四制八年级数学上册 19.3 勾股定理教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 75.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-16 00:00:00 | ||
图片预览

文档简介
勾股定理
教学目标
1.熟练掌握勾股定理的知识点2.掌握勾股定理的几大考点
重点、难点
勾股定理的灵活运用勾股定理与其他知识的交叉考察
教学内容
【知识回顾】考点一:利用求未知边。例1.在一直角三角形中有两边长分别是3、4,则其第三边长为
变式已知直角三角形的两边长为3、2,则另一条边长是________________.2.在一个直角三角形中,若斜边长为5cm,直角边的长为3cm,则另一条直角边的长为_______________.考点二:勾股数的考察例2.下面四组数中是勾股数的有(
).
(1)1.5,2.5,2
(2),,2
(3)12,16,20
(4)0.5,1.
2,1.3
A.1组
B.2组
C.3组
D.4组变式以下列各组数为边长,能组成直角三角形的是(
)
A.2,3,4
B.10,8,4
C.7,25,24
D.7,15,12考点四:直角三角形的判定问题例4、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c。试判断△ABC的形状。变式若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,试判断△ABC的形状。考点五:面积问题例5.已知:如图,已知∠B=∠D=90°,∠A=60°,AB=10,CD=6。求:四边形ABCD的面积。
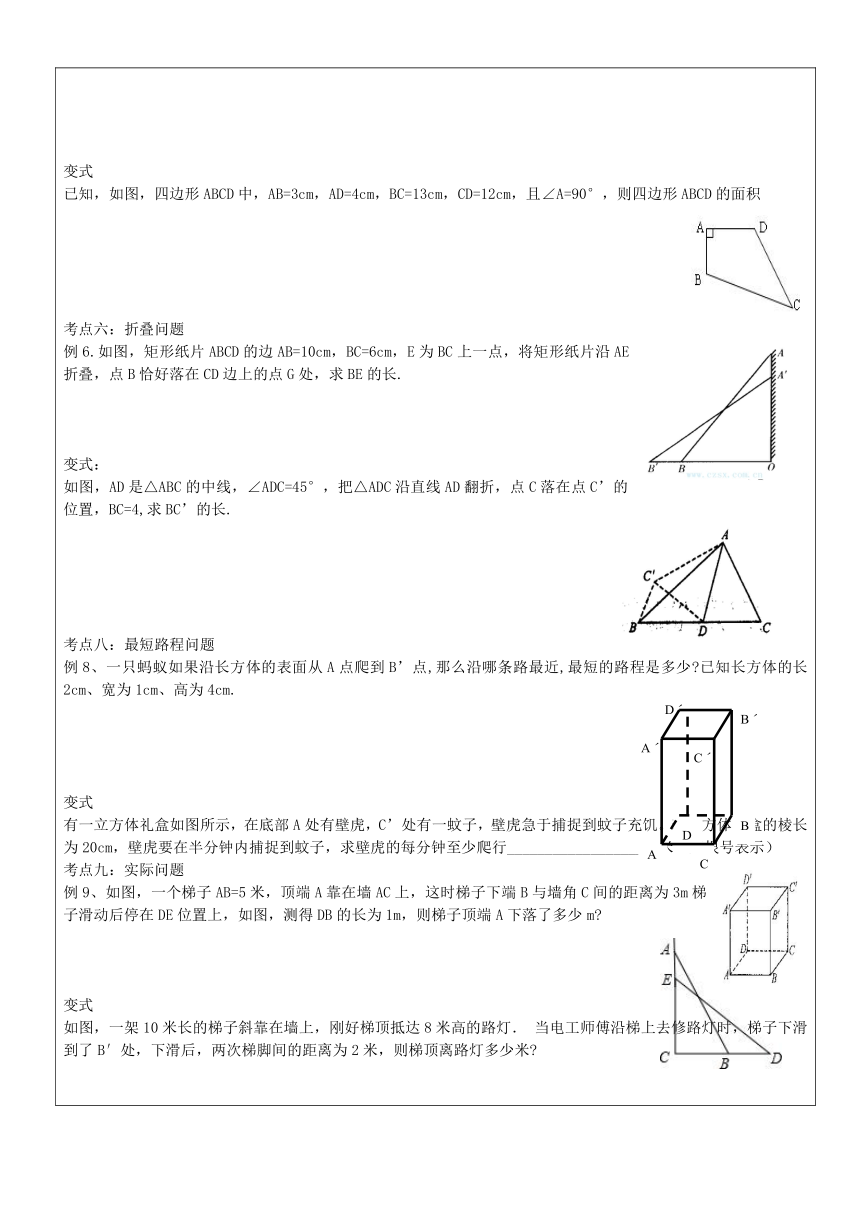
变式已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积考点六:折叠问题例6.如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.变式:如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,点C落在点C’的位置,BC=4,求BC’的长.考点八:最短路程问题例8、一只蚂蚁如果沿长方体的表面从A点爬到B’点,那么沿哪条路最近,最短的路程是多少 已知长方体的长2cm、宽为1cm、高为4cm.变式有一立方体礼盒如图所示,在底部A处有壁虎
( http: / / www.21cnjy.com ),C’处有一蚊子,壁虎急于捕捉到蚊子充饥。若立方体礼盒的棱长为20cm,壁虎要在半分钟内捕捉到蚊子,求壁虎的每分钟至少爬行__________________厘米(用根号表示)考点九:实际问题例9、如图,一个梯子AB=5米,顶端A靠在
( http: / / www.21cnjy.com )墙AC上,这时梯子下端B与墙角C间的距离为3m梯子滑动后停在DE位置上,如图,测得DB的长为1m,则梯子顶端A下落了多少m 变式如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米
考点十:思维发散例10.在中,,边上有2006个不同的点,记,则=_____.变式.细心观察下图,认真分析各式,然后解答问题.
()2+1=2
S1=()2+1=3
S2=
()2+4=5
S3=
(1)请用含n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;求出S12+S22+S22+…+S102的值.【家庭作业】1.已知△ABC中,∠A=∠B=∠C,则它的三条边之比为(
).
A.1:1:
B.1::2
C.1::
D.1:4:12.已知直角三角形一个锐角60°,斜边长为1,那么此直角三角形的周长是(
).
A.
B.3
C.
D.3.下列各组线段中,能够组成直角三角形的是(
).
A.6,7,8
B.5,6,7
C.4,5,6
D.3,4,54.下列各命题的逆命题成立的是(
)
A.全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等
D.如果两个角都是45°,那么这两个角相等5.若等边△ABC的边长为2cm,那么△ABC的面积为(
).
A.cm2
B.2cm2
C.3cm2
D.4cm26.在Rt△ABC中,已知其两直角边长a=1,b=3,那么斜边c的长为(
).
A.2
B.4
C.2
D.7.如图所示,△ABC中,CD⊥AB于D,若AD=2BD,AC=5,BC=4,则BD的长为(
).
B.
C.1
D.直角三角形有一条直角边长为13,另外两条边长都是自然数,则周长为(
)A.182
B.183
C.184
D.1859.如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,求CN的长
10.已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm,求EC的长.
A
B
C
D
Dˊ
A
B
C
D
Aˊ
Bˊ
Cˊ
教学目标
1.熟练掌握勾股定理的知识点2.掌握勾股定理的几大考点
重点、难点
勾股定理的灵活运用勾股定理与其他知识的交叉考察
教学内容
【知识回顾】考点一:利用求未知边。例1.在一直角三角形中有两边长分别是3、4,则其第三边长为
变式已知直角三角形的两边长为3、2,则另一条边长是________________.2.在一个直角三角形中,若斜边长为5cm,直角边的长为3cm,则另一条直角边的长为_______________.考点二:勾股数的考察例2.下面四组数中是勾股数的有(
).
(1)1.5,2.5,2
(2),,2
(3)12,16,20
(4)0.5,1.
2,1.3
A.1组
B.2组
C.3组
D.4组变式以下列各组数为边长,能组成直角三角形的是(
)
A.2,3,4
B.10,8,4
C.7,25,24
D.7,15,12考点四:直角三角形的判定问题例4、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c。试判断△ABC的形状。变式若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,试判断△ABC的形状。考点五:面积问题例5.已知:如图,已知∠B=∠D=90°,∠A=60°,AB=10,CD=6。求:四边形ABCD的面积。
变式已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积考点六:折叠问题例6.如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.变式:如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,点C落在点C’的位置,BC=4,求BC’的长.考点八:最短路程问题例8、一只蚂蚁如果沿长方体的表面从A点爬到B’点,那么沿哪条路最近,最短的路程是多少 已知长方体的长2cm、宽为1cm、高为4cm.变式有一立方体礼盒如图所示,在底部A处有壁虎
( http: / / www.21cnjy.com ),C’处有一蚊子,壁虎急于捕捉到蚊子充饥。若立方体礼盒的棱长为20cm,壁虎要在半分钟内捕捉到蚊子,求壁虎的每分钟至少爬行__________________厘米(用根号表示)考点九:实际问题例9、如图,一个梯子AB=5米,顶端A靠在
( http: / / www.21cnjy.com )墙AC上,这时梯子下端B与墙角C间的距离为3m梯子滑动后停在DE位置上,如图,测得DB的长为1m,则梯子顶端A下落了多少m 变式如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米
考点十:思维发散例10.在中,,边上有2006个不同的点,记,则=_____.变式.细心观察下图,认真分析各式,然后解答问题.
()2+1=2
S1=()2+1=3
S2=
()2+4=5
S3=
(1)请用含n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;求出S12+S22+S22+…+S102的值.【家庭作业】1.已知△ABC中,∠A=∠B=∠C,则它的三条边之比为(
).
A.1:1:
B.1::2
C.1::
D.1:4:12.已知直角三角形一个锐角60°,斜边长为1,那么此直角三角形的周长是(
).
A.
B.3
C.
D.3.下列各组线段中,能够组成直角三角形的是(
).
A.6,7,8
B.5,6,7
C.4,5,6
D.3,4,54.下列各命题的逆命题成立的是(
)
A.全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等
D.如果两个角都是45°,那么这两个角相等5.若等边△ABC的边长为2cm,那么△ABC的面积为(
).
A.cm2
B.2cm2
C.3cm2
D.4cm26.在Rt△ABC中,已知其两直角边长a=1,b=3,那么斜边c的长为(
).
A.2
B.4
C.2
D.7.如图所示,△ABC中,CD⊥AB于D,若AD=2BD,AC=5,BC=4,则BD的长为(
).
B.
C.1
D.直角三角形有一条直角边长为13,另外两条边长都是自然数,则周长为(
)A.182
B.183
C.184
D.1859.如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,求CN的长
10.已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm,求EC的长.
A
B
C
D
Dˊ
A
B
C
D
Aˊ
Bˊ
Cˊ
