沪教版五四制八年级数学上册 19.2 线段垂直平分线与角平分线教案(表格式)
文档属性
| 名称 | 沪教版五四制八年级数学上册 19.2 线段垂直平分线与角平分线教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-16 00:00:00 | ||
图片预览


文档简介
线段垂直平分线与角平分线
教学目标
线段垂直平分线与角平分线概念与定理以及逆定理的理解与应用
重点、难点
线段垂直平分线与角平分线定理与逆定理的理解与应用
考点及考试要求
定理与逆定理的应用
教学内容
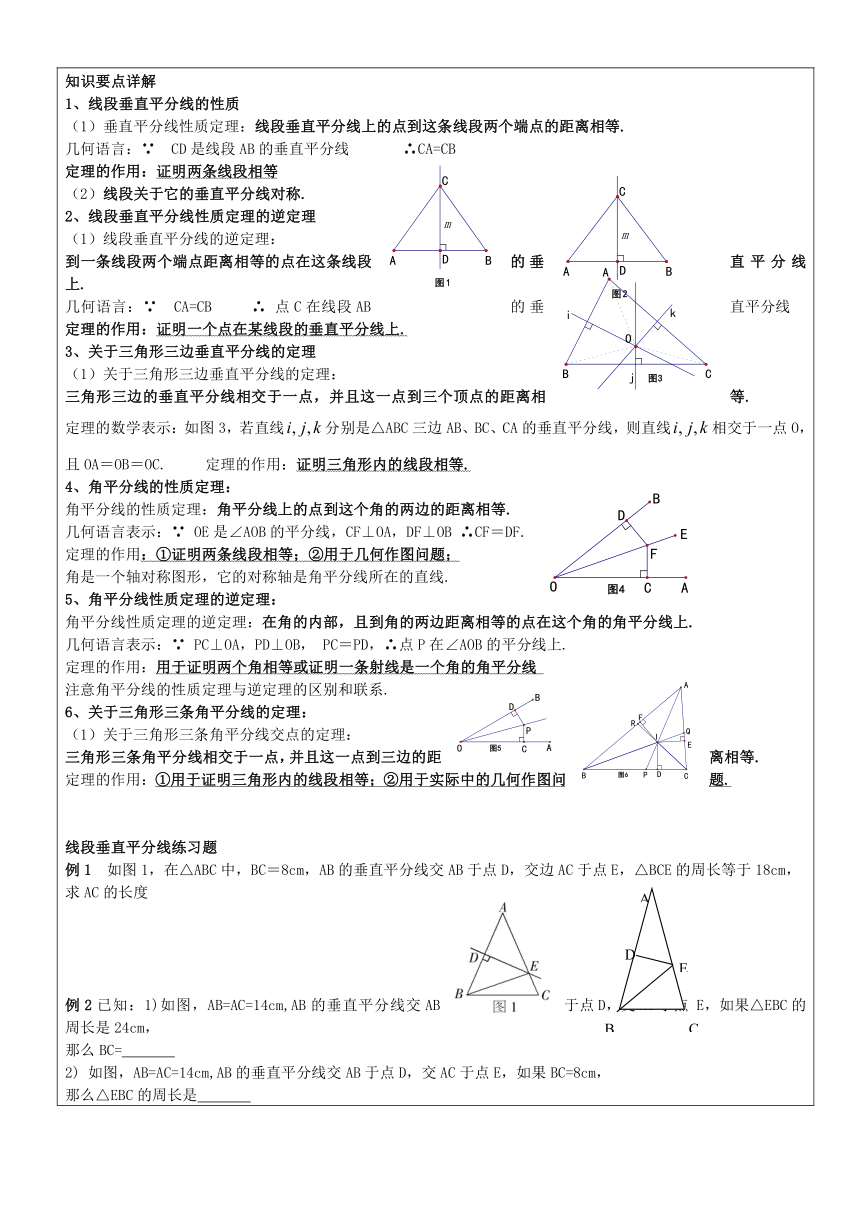
知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
几何语言:∵
CD是线段AB的垂直平分线
∴CA=CB定理的作用:证明两条线段相等(2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
几何语言:∵
CA=CB
∴
点C在线段AB的垂直平分线定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线分别是△ABC三边AB、BC、CA的垂直平分线,则直线相交于一点O,且OA=OB=OC.
定理的作用:证明三角形内的线段相等.4、角平分线的性质定理:角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.
几何语言表示:∵
OE是∠AOB的平分线,CF⊥OA,DF⊥OB
∴CF=DF.
定理的作用:①证明两条线段相等;②用于几何作图问题;角是一个轴对称图形,它的对称轴是角平分线所在的直线.5、角平分线性质定理的逆定理:角平分线性质定理的逆定理:在角的内部,且到角的两边距离相等的点在这个角的角平分线上.
几何语言表示:∵
PC⊥OA,PD⊥OB,
PC=PD,∴点P在∠AOB的平分线上.
定理的作用:用于证明两个角相等或证明一条射线是一个角的角平分线
注意角平分线的性质定理与逆定理的区别和联系.6、关于三角形三条角平分线的定理:(1)关于三角形三条角平分线交点的定理:三角形三条角平分线相交于一点,并且这一点到三边的距离相等.定理的作用:①用于证明三角形内的线段相等;②用于实际中的几何作图问题.线段垂直平分线练习题例1 如图1,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长度例2已知:1)如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点
E,如果△EBC的周长是24cm,那么BC=
2)
如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是
3)如图,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,如果∠A=28度,那么∠EBC是
例3、已知:在△ABC中,ON是AB的垂直平分线,OA=OC。
求证:点O在BC的垂直平分线
例4、如图8,已知AD是△ABC的BC边上的高,且∠C=2∠B,求证:BD=AC+CD.证明:练习1、如图,AC=AD,BC=BD,则(
)A.CD垂直平分AD
B.AB垂直平分CD
C.CD平分∠ACB
D.以上结论均不对2、如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是(
)A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形3、下列命题中正确的命题有(
)①线段垂直平分线上任一点到线段两端距离相
( http: / / www.21cnjy.com )等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P在线段AB外且PA=PB,过P作直线MN,则MN是线段AB的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.A.1个
B.2个
C.3个
D.4个4、已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.5、如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC、AB于点M、N.
求证:CM=2BM.
6、如图,在△ABC中,∠ABC=120°,点D是AB延长线和AC垂直平分线的交点。联接CD,这时BC恰好平分∠DCA。求∠A的度数。角平分线例题例1、已知:如图,点B、C在∠A的两边上,
( http: / / www.21cnjy.com )且AB=AC,P为∠A内一点,
PB=PC,PE⊥AC,PF⊥AB,垂足分别是E、F。求证:PE=PF例2、如图10,已知在四边形ABCD中,A
( http: / / www.21cnjy.com )B∥CD,AB⊥BC,EF⊥AD,E为BC中点,连接AE、DE,DE平分∠ADC,求证:AE平分∠BAD.例3、如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
练习1、
△ABC中,AB=AC,AC的中垂线交AB于E,△EBC的周长为20cm,AB=2BC,则腰长为________________。2、
如图所示,AB//CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD之间的距离等于______________。3、三角形中到三边距离相等的点是( )A、三条边的垂直平分线的交点
B、三条高的交点 C、三条中线的交点
D、三条角平分线的交点4、如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )A、PD=PE
B、OD=OE
C、∠DPO=∠EPO
D、PD=OD5、如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、4处
B、3处
C、2处 D、1处6、如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝,则△DEB的周长为( )
A、4㎝
B、6㎝
C、10㎝
D、不能确定
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
第4题
第5题
第6题
7、如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )A、TQ=PQ B、∠MQT=∠MQP C、∠QTN=90° D、∠NQT=∠MQT
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
第7题
第8题
第9题8、如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3
cm,那么AE+DE等于(
)
A.2
cm
B.3
cm
C.4
cm
D.5
cm
9、如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是(
)A.①
B.②
C.①和②
D.①②③10、如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.求证:AE平分∠FAC.12、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.家庭作业:一、选择题1.如图1,在△ABC中,AD平分∠CAE,∠B=,∠CAD=,则∠ACD等于
(
)A.
B.
C.
D.
2.如图2,在△ABD中,AD=4,AB=3,AC平分∠BAD,则=
(
)A.
B.
C.
D.不能确定3.如图3,在△ABC中,∠C=,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB。其中正确的有
(
)A.2个
B.3个
C.4个
D.1个4.如图4,AD∥BC,∠D=,AP平分∠DAB,PB平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是
(
)A.PD>PC
B.PDC.PD=PC
D.无法判断。5、在三角形内部,有一点P到三角形三个顶点的距离相等,则点P一定是
(
)A、三角形三条角平分线的交点;B、三角形三条垂直平分线的交点;C、三角形三条中线的交点;D、三角形三条高的交点。6、已知△ABC的三边的垂直平分线交点在△ABC的边上,则△ABC的形状为
(
)A、锐角三角形;B、直角三角形;C、钝角三角形;D、不能确定7、如图所示,在△ABC中
( http: / / www.21cnjy.com ),∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,F在BC上,并且BF=AB,则下列四个结论:①EF∥AC,②∠EFB=∠BAD,③AE=EF,④△ABE≌△FBE,其中正确的结论有
(
)A、①②③④ B、①③ C、②④ D、②③④7题图
8题图
9题图8、如图所示,在中,∠C=90°,
AC=4㎝,AB=7㎝,AD平分∠BAC交BC于D,DE⊥AB于E,则EB的长是
(
)A、3㎝ B、4㎝ C、5㎝ D、不能确定9、随着人们生活水平的不断提高,汽车逐
( http: / / www.21cnjy.com )步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有( )处。A、1 B、2 C、3 D、410、到三角形三条边的距离都相等的点是这个三角形的
(
)A.三条中线的交点
B.三条高的交点C.三条边的垂直平分线的交点
D.三条角平分线的交点二、填空题。1、如图,点在的平分线上,若使,则需添加的一个条件是
(只写一个即可,不添加辅助线):2、如图,△ABC中,DE、FG分别是边AB、AC的垂直平分线,BC=8则则△EAG的周长=
。3、如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是
。
第2题
第3题
4.
如图,在中,,平分,,那么点到直线的距离是 cm.5.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,若BD=10,则CD=
6.如图,△ABC中,AB=AC,
( http: / / www.21cnjy.com )DE是AB的垂直平分线,
AB=8,BC=4,∠A=36°,则∠DBC=
,△BDC的周长C△BDC
=
.7.如图,∠1=50°,∠2=80°,DB=AB,CE=CA,则∠D=
,∠DAE=
.8.如图,ΔABC的三边AB、BC、CA的长分别是20、30、40、其中三条角平分线将ΔABD分为三个三角形,则S:S:S等于______.三、解答题1.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.2.已知:E是∠AOB的平分线上一点,EC⊥OA
,ED⊥OB
,垂足分别为C、D.求证:(1)∠ECD=∠EDC
;(2)OE是CD的垂直平分线
B
C
D
E
A
B
N
A
B
C
O
图3
图4
图1
图2
1题
第8题
D
E
C
B
A
O
教学目标
线段垂直平分线与角平分线概念与定理以及逆定理的理解与应用
重点、难点
线段垂直平分线与角平分线定理与逆定理的理解与应用
考点及考试要求
定理与逆定理的应用
教学内容
知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
几何语言:∵
CD是线段AB的垂直平分线
∴CA=CB定理的作用:证明两条线段相等(2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
几何语言:∵
CA=CB
∴
点C在线段AB的垂直平分线定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线分别是△ABC三边AB、BC、CA的垂直平分线,则直线相交于一点O,且OA=OB=OC.
定理的作用:证明三角形内的线段相等.4、角平分线的性质定理:角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.
几何语言表示:∵
OE是∠AOB的平分线,CF⊥OA,DF⊥OB
∴CF=DF.
定理的作用:①证明两条线段相等;②用于几何作图问题;角是一个轴对称图形,它的对称轴是角平分线所在的直线.5、角平分线性质定理的逆定理:角平分线性质定理的逆定理:在角的内部,且到角的两边距离相等的点在这个角的角平分线上.
几何语言表示:∵
PC⊥OA,PD⊥OB,
PC=PD,∴点P在∠AOB的平分线上.
定理的作用:用于证明两个角相等或证明一条射线是一个角的角平分线
注意角平分线的性质定理与逆定理的区别和联系.6、关于三角形三条角平分线的定理:(1)关于三角形三条角平分线交点的定理:三角形三条角平分线相交于一点,并且这一点到三边的距离相等.定理的作用:①用于证明三角形内的线段相等;②用于实际中的几何作图问题.线段垂直平分线练习题例1 如图1,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长度例2已知:1)如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点
E,如果△EBC的周长是24cm,那么BC=
2)
如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是
3)如图,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,如果∠A=28度,那么∠EBC是
例3、已知:在△ABC中,ON是AB的垂直平分线,OA=OC。
求证:点O在BC的垂直平分线
例4、如图8,已知AD是△ABC的BC边上的高,且∠C=2∠B,求证:BD=AC+CD.证明:练习1、如图,AC=AD,BC=BD,则(
)A.CD垂直平分AD
B.AB垂直平分CD
C.CD平分∠ACB
D.以上结论均不对2、如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是(
)A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形3、下列命题中正确的命题有(
)①线段垂直平分线上任一点到线段两端距离相
( http: / / www.21cnjy.com )等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P在线段AB外且PA=PB,过P作直线MN,则MN是线段AB的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.A.1个
B.2个
C.3个
D.4个4、已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.5、如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC、AB于点M、N.
求证:CM=2BM.
6、如图,在△ABC中,∠ABC=120°,点D是AB延长线和AC垂直平分线的交点。联接CD,这时BC恰好平分∠DCA。求∠A的度数。角平分线例题例1、已知:如图,点B、C在∠A的两边上,
( http: / / www.21cnjy.com )且AB=AC,P为∠A内一点,
PB=PC,PE⊥AC,PF⊥AB,垂足分别是E、F。求证:PE=PF例2、如图10,已知在四边形ABCD中,A
( http: / / www.21cnjy.com )B∥CD,AB⊥BC,EF⊥AD,E为BC中点,连接AE、DE,DE平分∠ADC,求证:AE平分∠BAD.例3、如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
练习1、
△ABC中,AB=AC,AC的中垂线交AB于E,△EBC的周长为20cm,AB=2BC,则腰长为________________。2、
如图所示,AB//CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD之间的距离等于______________。3、三角形中到三边距离相等的点是( )A、三条边的垂直平分线的交点
B、三条高的交点 C、三条中线的交点
D、三条角平分线的交点4、如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )A、PD=PE
B、OD=OE
C、∠DPO=∠EPO
D、PD=OD5、如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、4处
B、3处
C、2处 D、1处6、如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝,则△DEB的周长为( )
A、4㎝
B、6㎝
C、10㎝
D、不能确定
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
第4题
第5题
第6题
7、如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )A、TQ=PQ B、∠MQT=∠MQP C、∠QTN=90° D、∠NQT=∠MQT
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
第7题
第8题
第9题8、如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3
cm,那么AE+DE等于(
)
A.2
cm
B.3
cm
C.4
cm
D.5
cm
9、如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是(
)A.①
B.②
C.①和②
D.①②③10、如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.求证:AE平分∠FAC.12、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.家庭作业:一、选择题1.如图1,在△ABC中,AD平分∠CAE,∠B=,∠CAD=,则∠ACD等于
(
)A.
B.
C.
D.
2.如图2,在△ABD中,AD=4,AB=3,AC平分∠BAD,则=
(
)A.
B.
C.
D.不能确定3.如图3,在△ABC中,∠C=,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB。其中正确的有
(
)A.2个
B.3个
C.4个
D.1个4.如图4,AD∥BC,∠D=,AP平分∠DAB,PB平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是
(
)A.PD>PC
B.PD
D.无法判断。5、在三角形内部,有一点P到三角形三个顶点的距离相等,则点P一定是
(
)A、三角形三条角平分线的交点;B、三角形三条垂直平分线的交点;C、三角形三条中线的交点;D、三角形三条高的交点。6、已知△ABC的三边的垂直平分线交点在△ABC的边上,则△ABC的形状为
(
)A、锐角三角形;B、直角三角形;C、钝角三角形;D、不能确定7、如图所示,在△ABC中
( http: / / www.21cnjy.com ),∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,F在BC上,并且BF=AB,则下列四个结论:①EF∥AC,②∠EFB=∠BAD,③AE=EF,④△ABE≌△FBE,其中正确的结论有
(
)A、①②③④ B、①③ C、②④ D、②③④7题图
8题图
9题图8、如图所示,在中,∠C=90°,
AC=4㎝,AB=7㎝,AD平分∠BAC交BC于D,DE⊥AB于E,则EB的长是
(
)A、3㎝ B、4㎝ C、5㎝ D、不能确定9、随着人们生活水平的不断提高,汽车逐
( http: / / www.21cnjy.com )步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有( )处。A、1 B、2 C、3 D、410、到三角形三条边的距离都相等的点是这个三角形的
(
)A.三条中线的交点
B.三条高的交点C.三条边的垂直平分线的交点
D.三条角平分线的交点二、填空题。1、如图,点在的平分线上,若使,则需添加的一个条件是
(只写一个即可,不添加辅助线):2、如图,△ABC中,DE、FG分别是边AB、AC的垂直平分线,BC=8则则△EAG的周长=
。3、如图,△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是
。
第2题
第3题
4.
如图,在中,,平分,,那么点到直线的距离是 cm.5.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,若BD=10,则CD=
6.如图,△ABC中,AB=AC,
( http: / / www.21cnjy.com )DE是AB的垂直平分线,
AB=8,BC=4,∠A=36°,则∠DBC=
,△BDC的周长C△BDC
=
.7.如图,∠1=50°,∠2=80°,DB=AB,CE=CA,则∠D=
,∠DAE=
.8.如图,ΔABC的三边AB、BC、CA的长分别是20、30、40、其中三条角平分线将ΔABD分为三个三角形,则S:S:S等于______.三、解答题1.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.2.已知:E是∠AOB的平分线上一点,EC⊥OA
,ED⊥OB
,垂足分别为C、D.求证:(1)∠ECD=∠EDC
;(2)OE是CD的垂直平分线
B
C
D
E
A
B
N
A
B
C
O
图3
图4
图1
图2
1题
第8题
D
E
C
B
A
O
