八年级数学上册 19.1 几何证明教案 沪教版五四制
文档属性
| 名称 | 八年级数学上册 19.1 几何证明教案 沪教版五四制 |  | |
| 格式 | zip | ||
| 文件大小 | 51.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-16 17:11:57 | ||
图片预览


文档简介
几何证明
教学目标
会证明直角三角形的全等;
HL;角平分线的性质与判定;线段垂直平分线的性质与判定;勾股定理与逆定理的应用。
重点、难点
线段垂直平分线与角平分线,直角三角形,勾股定理的综合应用
考点及考试要求
线段垂直平分线与角平分线,直角三角形,勾股定理的综合应用
教学内容
【一、知识点回顾】:1.一个命题是由
和
组成。2.正确的命题称为
命题,错误的命题称为
命题。【二、针对练习】(一)填空题1.把下列命题改写成“如果……,那么……”的形式,并判断其真假:(1)同位角相等,两直线平行。
(2)同角的余角相等。
(3)平角都相等。
(4)等腰三角形顶角的平分线是底边上的高。
2.举反例证明下列命题是假命题:(1)两个互余的角不相等。
(2)素数都是奇数。(3)同位角相等。
(4)如果x2=y2,那么x=y。3.如图,把定理“三角形的三个内角和等于180°”,改写成已知:
,求证:
。4.如图,“求证:等腰三角形两腰上的高相等”改写成已知:
,求证:
。5.全等三角形的对应
相等,对应
相等。6.等腰三角形的
角相等。等腰三角形的
互相重合
。7.如图,已知△ABF≌△DCE,则∠C=
,BF∥
.8.如图,点E、F在AD上,AE=DF,
( http: / / www.21cnjy.com )AB∥CD,要使△ABF≌△DCE,还需要添加条件
(A.S.A),
(A.A.S).(二)证明题1.如图,已知AB=AC,AD=AE,
∠1=∠2.求证:∠B=∠C.2.如图,D、E在的边BC上,AB=AC,(1)BD=CE,求证:
AD=AE.(2)AD=AE,求证:BD=CE.3.求证:等腰三角形两腰上的中线相等.【线段的垂直平分线与角的平分线】【一、知识点回顾】线段垂直平分线的定理:线段垂直平分线上的
到
的距离相等.2.线段垂直平分线的逆定理:
和一条线段
相等的点,在这条线段的
上.3.线段的垂直平分线可以看作是
的点的集合.4.角的平分线的定理:在角的平分线上的点到
的距离相等.5.角的平分线的逆定理:在一个角的
且
距离相等的点,在这个角的
上.6.角的平分线可以看作是
的点的集合.7.我们把符合
的所有点的集合叫做点的轨迹.8.(1)
的点的轨迹是这条线段的垂直平分线.
(2)
的点的轨迹是这个角的平分线.
(3)
的点的轨迹是以
为圆心、
为半径的圆.【二、针对练习】(一)填空题1.把下列命题改成逆命题并判断逆命题的真假.(1)对顶角相等.
(2)全都三角形对应角相等.(3)等腰三角形的两个底角相等.(4)直角三角形的两个锐角互余.2.如图,在中,AB=AC,
∠A=50°,DE为AB的垂直平分线,那么∠DBC=
°3.如图,在中,∠C=90°,∠CAB的平分线AD交BC于D,BC=10,BD=7,那么点D到AB的距离是
4.平面内与点A的距离等于3厘米的点的轨迹是
.5.底边给定等腰三角形顶点的轨迹
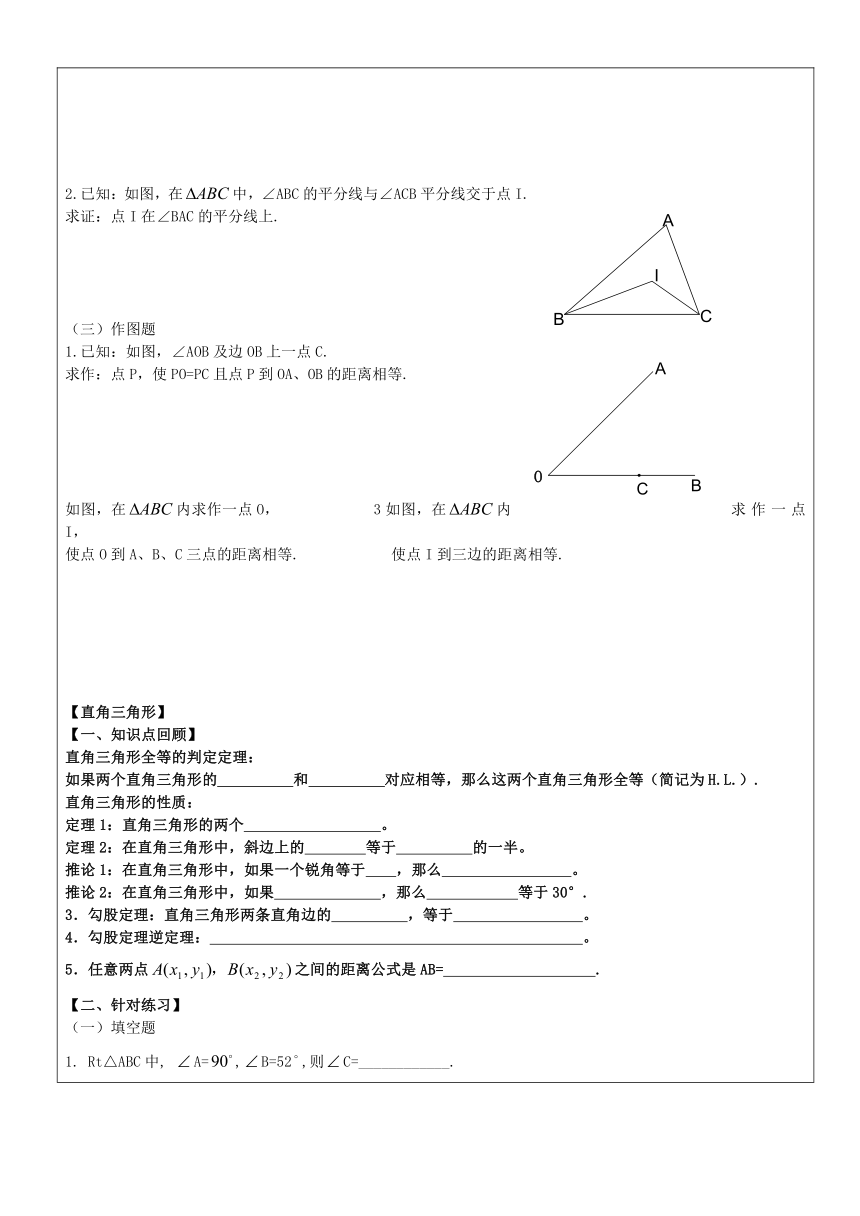
.(二)解答题和证明题1.如图,在中,的中垂线交于点,交BC于点E.求的周长2.已知:如图,在中,∠ABC的平分线与∠ACB平分线交于点I.求证:点I在∠BAC的平分线上.(三)作图题1.已知:如图,∠AOB及边OB上一点C.求作:点P,使PO=PC且点P到OA、OB的距离相等.如图,在内求作一点O,
3如图,在内求作一点I,使点O到A、B、C三点的距离相等.
使点I到三边的距离相等.【直角三角形】【一、知识点回顾】直角三角形全等的判定定理:如果两个直角三角形的
和
对应相等,那么这两个直角三角形全等(简记为H.L.).直角三角形的性质:定理1:直角三角形的两个
。定理2:在直角三角形中,斜边上的
等于
的一半。推论1:在直角三角形中,如果一个锐角等于
,那么
。推论2:在直角三角形中,如果
,那么
等于30°.3.勾股定理:直角三角形两条直角边的
,等于
。4.勾股定理逆定理:
。5.任意两点之间的距离公式是AB=
.【二、针对练习】(一)填空题1.
Rt△ABC中,
A=,B=52,则C=____________.2.Rt△ABC中,
C=90,a=5,b=12,则c=_____________.3.如图,在中,于D,则
;4.如图,在中,于,
则
;5.如图,在中,是中点,,那么
;6.如图,在中,D是中点,若
那么A
;7.如果直角三角形的两条直角边分别是则斜边上的中线是
;8.Rt△ABC中,
C=,CD是斜边AB上的的高,若AC=6,BC=8,则CD=_______.9.△ABC中,AB=AC,AD是BC边上中线,若AB=13,BC=10,则AD=__________.10.△ABC中,如果AB=,BC=8,AC=4,那么A的度数是____________.11.点A(-1,-2)与点B(2,-6)间的距离为
.12.点A(-3,0)与点B(1,0)间的距离为
.(二)简答题和证明题1.直角三角形斜边上的中线与斜边上的高分别是;求这个直角三角形的面积.2.如图,已知在△ABC中,AB=AC=16,
A=120,DE垂直平分AB,D为垂足.求DE的长.
已知:如图,BD、CE分别是AC、AB的高,P、Q分别是BC、ED的中点.求证:PQ⊥DE.基本方法:1、几何证明的分析思路:从结论出发,即:根据所要证明的结论,去寻找条件。例如:要证线段相等,则必先
( http: / / www.21cnjy.com )证:①⊿全等,然后利用全等三角形性质得到线段相等;②角相等,然后利用等角对等边(前提:在同一个三角形中)③寻找中间变量,然后利用等量代换得出结论;④观察图形,看是否可以直接利用线段的垂直平分线定理或角平分线定理来得出结论。
要证角相等,则必先证:①⊿全等
( http: / / www.21cnjy.com ),然后利用全等三角形性质得到角相等;②线段相等,然后利用等边对等角(前提:在同一个三角形中)③寻找中间变量,然后利用等量代换得出结论;④观察图形,看是否可以直接利用角平分线逆定理来得出结论。
要证垂直,则必先证:①两条直线所夹的角为90°;②先证等腰三角形,然后利用“三线合一”来得出结论(前提:在同一个三角形中)
要证三角形全等,则必先要从已知找条件,看要判定全等还却什么条件,然后再去寻找!从已知出发,即:根据所给条件、利用相关定理→→直接可得的结论。例如:已知线段的垂直平分线→→线段相等。
已知角平分线→→到角的两边距离相等或角相等。【家庭作业:】1、在直角坐标平面内,点A的坐标是(3,-2),点B的坐标是(a,2),如果AB=5,那么a=
。2、已知等腰的斜边BC的长是2,为等边三角形,那么A、D两点的距离是
。3、已知,如图在中,,,等腰直角三角形BEF的斜边在AB上,点G是AF的中点,联结EG、CG,求证:。
4、已知,如图,点P是内一点,,A、B分别为垂足,,求证:OP是的平分线。
签字确认
学员
教师
班主任
第3、4题
第5、6题
教学目标
会证明直角三角形的全等;
HL;角平分线的性质与判定;线段垂直平分线的性质与判定;勾股定理与逆定理的应用。
重点、难点
线段垂直平分线与角平分线,直角三角形,勾股定理的综合应用
考点及考试要求
线段垂直平分线与角平分线,直角三角形,勾股定理的综合应用
教学内容
【一、知识点回顾】:1.一个命题是由
和
组成。2.正确的命题称为
命题,错误的命题称为
命题。【二、针对练习】(一)填空题1.把下列命题改写成“如果……,那么……”的形式,并判断其真假:(1)同位角相等,两直线平行。
(2)同角的余角相等。
(3)平角都相等。
(4)等腰三角形顶角的平分线是底边上的高。
2.举反例证明下列命题是假命题:(1)两个互余的角不相等。
(2)素数都是奇数。(3)同位角相等。
(4)如果x2=y2,那么x=y。3.如图,把定理“三角形的三个内角和等于180°”,改写成已知:
,求证:
。4.如图,“求证:等腰三角形两腰上的高相等”改写成已知:
,求证:
。5.全等三角形的对应
相等,对应
相等。6.等腰三角形的
角相等。等腰三角形的
互相重合
。7.如图,已知△ABF≌△DCE,则∠C=
,BF∥
.8.如图,点E、F在AD上,AE=DF,
( http: / / www.21cnjy.com )AB∥CD,要使△ABF≌△DCE,还需要添加条件
(A.S.A),
(A.A.S).(二)证明题1.如图,已知AB=AC,AD=AE,
∠1=∠2.求证:∠B=∠C.2.如图,D、E在的边BC上,AB=AC,(1)BD=CE,求证:
AD=AE.(2)AD=AE,求证:BD=CE.3.求证:等腰三角形两腰上的中线相等.【线段的垂直平分线与角的平分线】【一、知识点回顾】线段垂直平分线的定理:线段垂直平分线上的
到
的距离相等.2.线段垂直平分线的逆定理:
和一条线段
相等的点,在这条线段的
上.3.线段的垂直平分线可以看作是
的点的集合.4.角的平分线的定理:在角的平分线上的点到
的距离相等.5.角的平分线的逆定理:在一个角的
且
距离相等的点,在这个角的
上.6.角的平分线可以看作是
的点的集合.7.我们把符合
的所有点的集合叫做点的轨迹.8.(1)
的点的轨迹是这条线段的垂直平分线.
(2)
的点的轨迹是这个角的平分线.
(3)
的点的轨迹是以
为圆心、
为半径的圆.【二、针对练习】(一)填空题1.把下列命题改成逆命题并判断逆命题的真假.(1)对顶角相等.
(2)全都三角形对应角相等.(3)等腰三角形的两个底角相等.(4)直角三角形的两个锐角互余.2.如图,在中,AB=AC,
∠A=50°,DE为AB的垂直平分线,那么∠DBC=
°3.如图,在中,∠C=90°,∠CAB的平分线AD交BC于D,BC=10,BD=7,那么点D到AB的距离是
4.平面内与点A的距离等于3厘米的点的轨迹是
.5.底边给定等腰三角形顶点的轨迹
.(二)解答题和证明题1.如图,在中,的中垂线交于点,交BC于点E.求的周长2.已知:如图,在中,∠ABC的平分线与∠ACB平分线交于点I.求证:点I在∠BAC的平分线上.(三)作图题1.已知:如图,∠AOB及边OB上一点C.求作:点P,使PO=PC且点P到OA、OB的距离相等.如图,在内求作一点O,
3如图,在内求作一点I,使点O到A、B、C三点的距离相等.
使点I到三边的距离相等.【直角三角形】【一、知识点回顾】直角三角形全等的判定定理:如果两个直角三角形的
和
对应相等,那么这两个直角三角形全等(简记为H.L.).直角三角形的性质:定理1:直角三角形的两个
。定理2:在直角三角形中,斜边上的
等于
的一半。推论1:在直角三角形中,如果一个锐角等于
,那么
。推论2:在直角三角形中,如果
,那么
等于30°.3.勾股定理:直角三角形两条直角边的
,等于
。4.勾股定理逆定理:
。5.任意两点之间的距离公式是AB=
.【二、针对练习】(一)填空题1.
Rt△ABC中,
A=,B=52,则C=____________.2.Rt△ABC中,
C=90,a=5,b=12,则c=_____________.3.如图,在中,于D,则
;4.如图,在中,于,
则
;5.如图,在中,是中点,,那么
;6.如图,在中,D是中点,若
那么A
;7.如果直角三角形的两条直角边分别是则斜边上的中线是
;8.Rt△ABC中,
C=,CD是斜边AB上的的高,若AC=6,BC=8,则CD=_______.9.△ABC中,AB=AC,AD是BC边上中线,若AB=13,BC=10,则AD=__________.10.△ABC中,如果AB=,BC=8,AC=4,那么A的度数是____________.11.点A(-1,-2)与点B(2,-6)间的距离为
.12.点A(-3,0)与点B(1,0)间的距离为
.(二)简答题和证明题1.直角三角形斜边上的中线与斜边上的高分别是;求这个直角三角形的面积.2.如图,已知在△ABC中,AB=AC=16,
A=120,DE垂直平分AB,D为垂足.求DE的长.
已知:如图,BD、CE分别是AC、AB的高,P、Q分别是BC、ED的中点.求证:PQ⊥DE.基本方法:1、几何证明的分析思路:从结论出发,即:根据所要证明的结论,去寻找条件。例如:要证线段相等,则必先
( http: / / www.21cnjy.com )证:①⊿全等,然后利用全等三角形性质得到线段相等;②角相等,然后利用等角对等边(前提:在同一个三角形中)③寻找中间变量,然后利用等量代换得出结论;④观察图形,看是否可以直接利用线段的垂直平分线定理或角平分线定理来得出结论。
要证角相等,则必先证:①⊿全等
( http: / / www.21cnjy.com ),然后利用全等三角形性质得到角相等;②线段相等,然后利用等边对等角(前提:在同一个三角形中)③寻找中间变量,然后利用等量代换得出结论;④观察图形,看是否可以直接利用角平分线逆定理来得出结论。
要证垂直,则必先证:①两条直线所夹的角为90°;②先证等腰三角形,然后利用“三线合一”来得出结论(前提:在同一个三角形中)
要证三角形全等,则必先要从已知找条件,看要判定全等还却什么条件,然后再去寻找!从已知出发,即:根据所给条件、利用相关定理→→直接可得的结论。例如:已知线段的垂直平分线→→线段相等。
已知角平分线→→到角的两边距离相等或角相等。【家庭作业:】1、在直角坐标平面内,点A的坐标是(3,-2),点B的坐标是(a,2),如果AB=5,那么a=
。2、已知等腰的斜边BC的长是2,为等边三角形,那么A、D两点的距离是
。3、已知,如图在中,,,等腰直角三角形BEF的斜边在AB上,点G是AF的中点,联结EG、CG,求证:。
4、已知,如图,点P是内一点,,A、B分别为垂足,,求证:OP是的平分线。
签字确认
学员
教师
班主任
第3、4题
第5、6题
