10.2 三角形的内角和外角 第1课时 课件(共30张PPT)
文档属性
| 名称 | 10.2 三角形的内角和外角 第1课时 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
10.2 三角形的内角和外角
第十章 三角形
1.经历探索三角形内角和定理的过程,能说明三角形内角和定理,提高推理能力。
2.理解三角形外角的概念,经历三角形外角与内角之间关系的探究过程,掌握三角形内角和定理的推论,并能应用三角形内角和定理及其推论解决相关问题。
3.了解锐角三角形、直角三角形和钝角三角形的概念,能将三角形按角进行分类。
学习目标
目录
问题引入
1
三角形内角和定理
2
当堂练习
3
课堂小结
4
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.你知道其中的道理吗?
内角三兄弟之争
问题引入
1
问题1
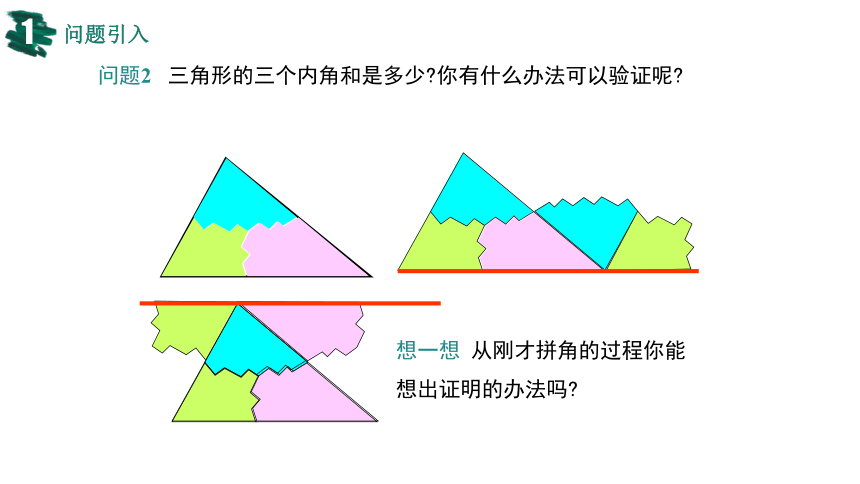
问题2 三角形的三个内角和是多少 你有什么办法可以验证呢
想一想 从刚才拼角的过程你能想出证明的办法吗
问题引入
1
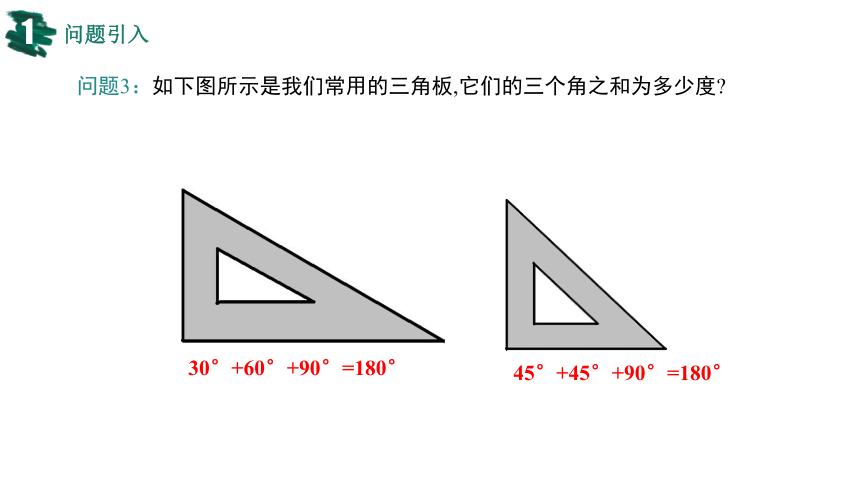
问题3:如下图所示是我们常用的三角板,它们的三个角之和为多少度
30°+60°+90°=180°
45°+45°+90°=180°
问题引入
1
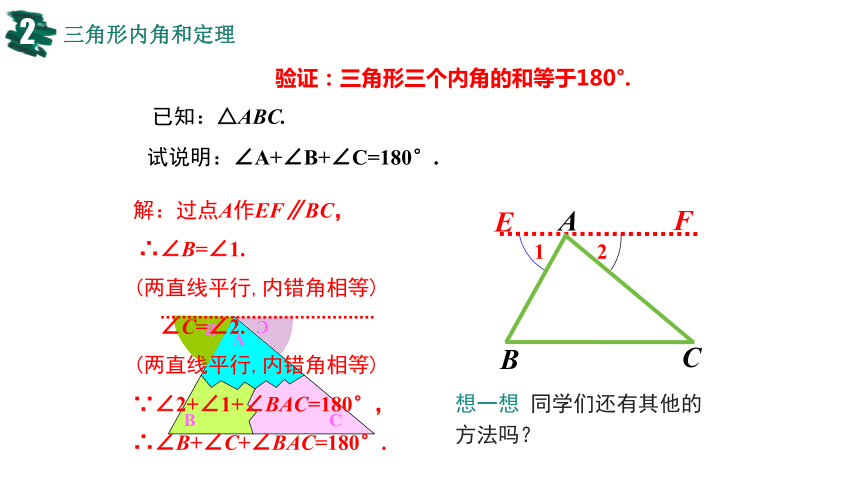
验证:三角形三个内角的和等于180°.
F
2
1
E
C
B
A
试说明:∠A+∠B+∠C=180°.
已知:△ABC.
A
C
B
C
B
解:过点A作EF∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
想一想 同学们还有其他的方法吗?
三角形内角和定理
2
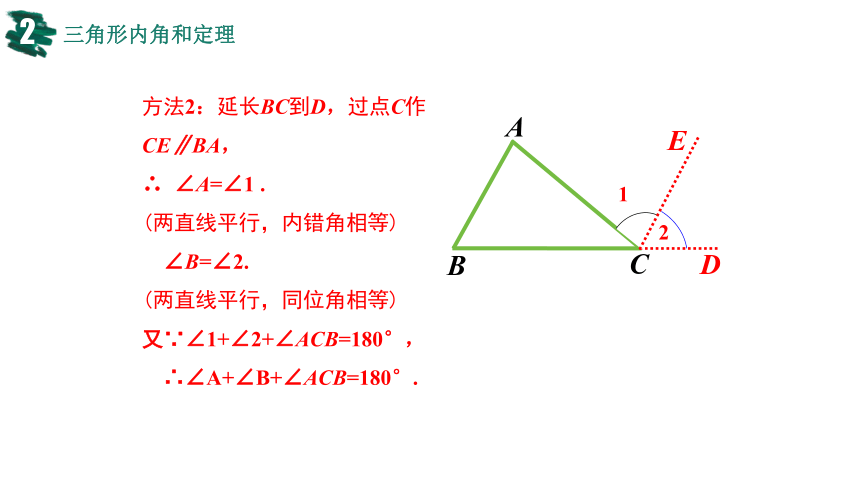
方法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
三角形内角和定理
2
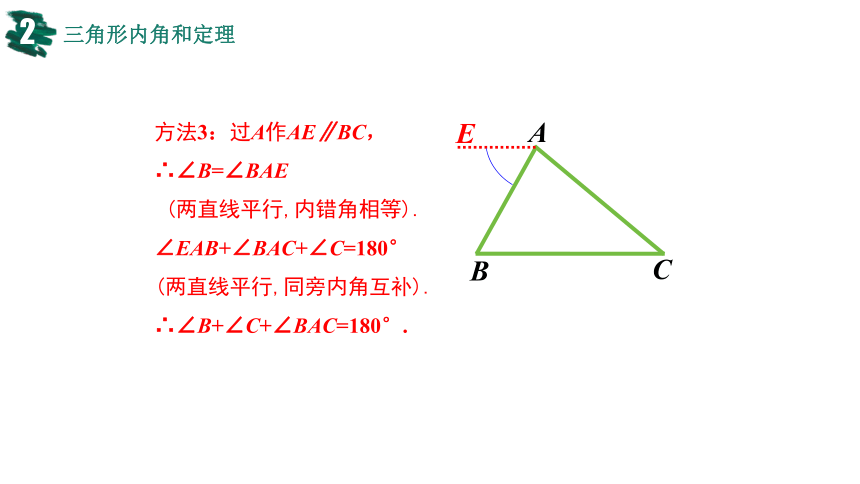
方法3:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等).
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补).
∴∠B+∠C+∠BAC=180°.
C
B
A
E
三角形内角和定理
2
例1 如图,在△ABC中,∠A=30°,∠B=65°,求∠C的度数.
A
B
C
解:∵∠A+∠B+∠C=180°(三角形的内角和定理),
∴∠C=180°-(∠A+∠B).
∵∠A=30°,∠B=65°,(已知)
∴∠C=180°-(30°+65°)=85°.
三角形内角和定理
2
典例精析
(2) 在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是 三角形 .
(1) 在△ABC中,∠A=35°,∠ B=43 °,则∠ C= .
(3) 在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则
∠A= , ∠ B= ,∠ C= .
102°
直角
60°
50°
70°
随堂训练
三角形内角和定理
2
如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
随堂训练
三角形内角和定理
2
例2 在△ABC 中,∠A∶∠B∶∠C=1∶2∶3,试判断△ABC 的形状,并说明理由.
三角形内角和定理
2
典例精析
△ABC 是直角三角形.理由如下:
∵∠A∶∠B∶∠C=1∶2∶3,
∴可设∠A,∠B,∠C 的度数分别为x °,2x °,3x °.在△ABC 中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°),
∴x+2x+3x=180,解得x=30.
∴∠C=3x°=90°,
∴△ABC 是直角三角形.
解:
三角形内角和定理
2
配套练习
北
.
A
D
北
.
C
B
.
东
E
例3 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向,从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
典例精析
三角形内角和定理
2
解:∠CAB= ∠BAD-∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °-∠BAD=180°-80°
=100°,∠ABC= ∠ABE- ∠EBC=100°-40°=60°.
在△ABC中,
∠ACB=180 °-∠ABC-∠ CAB
=180°-60°-30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°.
北
.
A
D
北
.
C
B
.
东
E
三角形内角和定理
2
三角形内角和定理
2
配套练习
如图,A 点在B 点的北偏东40°方向,C 点在B 点的北偏东75°方向,A 点在C 点的北偏西50°方向.
(1)试说明△ABC 为直角三角形;
(2)求∠BCA 的度数.
三角形内角和定理
2
(1)如图,过A 作AF∥BD,∴∠BAF=∠ABD=40°.显然AF∥EC,
∴∠CAF=∠ECA=50°.
∴∠BAC=∠BAF+∠CAF=40°+50°=90°.
∴△ABC 为直角三角形.
(2)∵∠DBC=75°,∠DBA=40°,
∴∠ABC=∠DBC-∠DBA=75°-40°=35°.
∴在Rt△ABC中,∠BCA=90°-∠ABC=90°-35°=55°.
解:
当堂练习
3
当堂练习
3
当堂练习
3
当堂练习
3
当堂练习
3
当堂练习
3
如图,说明∠A+∠B+∠C 与∠ADC 之间的关系.
易错点:非三角形问题用内角和定理而致错
当堂练习
3
易错提醒
解:
连接BD.∵∠A+∠ABD+∠ADB=180°,
∠C+∠DBC+∠CDB=180°,
∴∠A+∠ABD+∠ADB+∠C+∠DBC+∠CDB=360°,
又∵∠ADB+∠CDB+∠ADC=360°,
∴∠A+∠ABC+∠C+360°-∠ADC=360°,
∴∠A+∠ABC+∠C=∠ADC.
当堂练习
3
7.说出下列各图中的x值.
x=70
x=60
x=30
x=50
当堂练习
3
8.如图,则∠1+∠2+∠3+∠4=___________ .
B
A
C
D
4
1
3
2
E
40°
(
280 °
解析:根据三角形的内角和定理,∠A+∠1+∠2=180°,∠3+∠4+∠A=180°,∴∠1+∠2=∠3+∠4=180°-∠A
=140°,∴∠1+∠2+∠3+∠4=280°.
当堂练习
3
9.如图,在△ABC 中,∠ ABC ,∠ ACB 的平分线BD,CE 交于点O.
变式1 若∠A =80°,则∠BOC = .
变式2 你能直接写出∠BOC与∠A 之间的数量关
系吗?
A
B
C
O
E
D
130°
∠BOC = 90°+ ∠A .
当堂练习
3
三角形的内角和定理
内容
应用
三角形的内角和等于180°.
通过作辅助线,结合平行线的性质,验证定理
求三角形的内角度数.
课堂小结
4
10.2 三角形的内角和外角
第十章 三角形
1.经历探索三角形内角和定理的过程,能说明三角形内角和定理,提高推理能力。
2.理解三角形外角的概念,经历三角形外角与内角之间关系的探究过程,掌握三角形内角和定理的推论,并能应用三角形内角和定理及其推论解决相关问题。
3.了解锐角三角形、直角三角形和钝角三角形的概念,能将三角形按角进行分类。
学习目标
目录
问题引入
1
三角形内角和定理
2
当堂练习
3
课堂小结
4
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.你知道其中的道理吗?
内角三兄弟之争
问题引入
1
问题1
问题2 三角形的三个内角和是多少 你有什么办法可以验证呢
想一想 从刚才拼角的过程你能想出证明的办法吗
问题引入
1
问题3:如下图所示是我们常用的三角板,它们的三个角之和为多少度
30°+60°+90°=180°
45°+45°+90°=180°
问题引入
1
验证:三角形三个内角的和等于180°.
F
2
1
E
C
B
A
试说明:∠A+∠B+∠C=180°.
已知:△ABC.
A
C
B
C
B
解:过点A作EF∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
想一想 同学们还有其他的方法吗?
三角形内角和定理
2
方法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
三角形内角和定理
2
方法3:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等).
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补).
∴∠B+∠C+∠BAC=180°.
C
B
A
E
三角形内角和定理
2
例1 如图,在△ABC中,∠A=30°,∠B=65°,求∠C的度数.
A
B
C
解:∵∠A+∠B+∠C=180°(三角形的内角和定理),
∴∠C=180°-(∠A+∠B).
∵∠A=30°,∠B=65°,(已知)
∴∠C=180°-(30°+65°)=85°.
三角形内角和定理
2
典例精析
(2) 在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是 三角形 .
(1) 在△ABC中,∠A=35°,∠ B=43 °,则∠ C= .
(3) 在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则
∠A= , ∠ B= ,∠ C= .
102°
直角
60°
50°
70°
随堂训练
三角形内角和定理
2
如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
随堂训练
三角形内角和定理
2
例2 在△ABC 中,∠A∶∠B∶∠C=1∶2∶3,试判断△ABC 的形状,并说明理由.
三角形内角和定理
2
典例精析
△ABC 是直角三角形.理由如下:
∵∠A∶∠B∶∠C=1∶2∶3,
∴可设∠A,∠B,∠C 的度数分别为x °,2x °,3x °.在△ABC 中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°),
∴x+2x+3x=180,解得x=30.
∴∠C=3x°=90°,
∴△ABC 是直角三角形.
解:
三角形内角和定理
2
配套练习
北
.
A
D
北
.
C
B
.
东
E
例3 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向,从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
典例精析
三角形内角和定理
2
解:∠CAB= ∠BAD-∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °-∠BAD=180°-80°
=100°,∠ABC= ∠ABE- ∠EBC=100°-40°=60°.
在△ABC中,
∠ACB=180 °-∠ABC-∠ CAB
=180°-60°-30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°.
北
.
A
D
北
.
C
B
.
东
E
三角形内角和定理
2
三角形内角和定理
2
配套练习
如图,A 点在B 点的北偏东40°方向,C 点在B 点的北偏东75°方向,A 点在C 点的北偏西50°方向.
(1)试说明△ABC 为直角三角形;
(2)求∠BCA 的度数.
三角形内角和定理
2
(1)如图,过A 作AF∥BD,∴∠BAF=∠ABD=40°.显然AF∥EC,
∴∠CAF=∠ECA=50°.
∴∠BAC=∠BAF+∠CAF=40°+50°=90°.
∴△ABC 为直角三角形.
(2)∵∠DBC=75°,∠DBA=40°,
∴∠ABC=∠DBC-∠DBA=75°-40°=35°.
∴在Rt△ABC中,∠BCA=90°-∠ABC=90°-35°=55°.
解:
当堂练习
3
当堂练习
3
当堂练习
3
当堂练习
3
当堂练习
3
当堂练习
3
如图,说明∠A+∠B+∠C 与∠ADC 之间的关系.
易错点:非三角形问题用内角和定理而致错
当堂练习
3
易错提醒
解:
连接BD.∵∠A+∠ABD+∠ADB=180°,
∠C+∠DBC+∠CDB=180°,
∴∠A+∠ABD+∠ADB+∠C+∠DBC+∠CDB=360°,
又∵∠ADB+∠CDB+∠ADC=360°,
∴∠A+∠ABC+∠C+360°-∠ADC=360°,
∴∠A+∠ABC+∠C=∠ADC.
当堂练习
3
7.说出下列各图中的x值.
x=70
x=60
x=30
x=50
当堂练习
3
8.如图,则∠1+∠2+∠3+∠4=___________ .
B
A
C
D
4
1
3
2
E
40°
(
280 °
解析:根据三角形的内角和定理,∠A+∠1+∠2=180°,∠3+∠4+∠A=180°,∴∠1+∠2=∠3+∠4=180°-∠A
=140°,∴∠1+∠2+∠3+∠4=280°.
当堂练习
3
9.如图,在△ABC 中,∠ ABC ,∠ ACB 的平分线BD,CE 交于点O.
变式1 若∠A =80°,则∠BOC = .
变式2 你能直接写出∠BOC与∠A 之间的数量关
系吗?
A
B
C
O
E
D
130°
∠BOC = 90°+ ∠A .
当堂练习
3
三角形的内角和定理
内容
应用
三角形的内角和等于180°.
通过作辅助线,结合平行线的性质,验证定理
求三角形的内角度数.
课堂小结
4
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
