2025年中考数学复习专练:第八章 函数(含答案)
文档属性
| 名称 | 2025年中考数学复习专练:第八章 函数(含答案) | 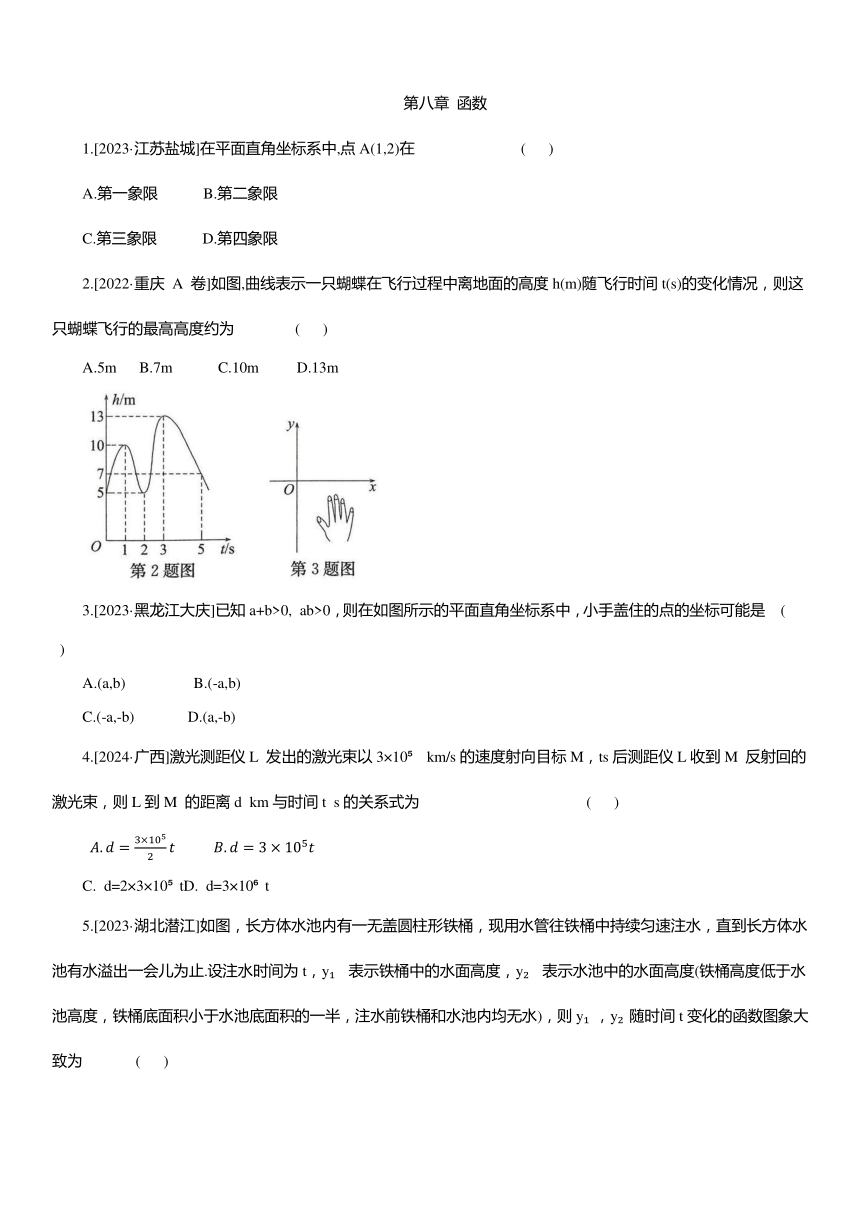 | |
| 格式 | docx | ||
| 文件大小 | 137.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 21:24:56 | ||
图片预览



文档简介
第八章 函数
1.[2023·江苏盐城]在平面直角坐标系中,点A(1,2)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.[2022·重庆 A 卷]如图,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间t(s)的变化情况,则这只蝴蝶飞行的最高高度约为 ( )
A.5m B.7m C.10m D.13m
3.[2023·黑龙江大庆]已知a+b>0, ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是 ( )
A.(a,b) B.(-a,b)
C.(-a,-b) D.(a,-b)
4.[2024·广西]激光测距仪L 发出的激光束以3×10 km/s的速度射向目标M,ts后测距仪L收到M 反射回的激光束,则L到M 的距离d km与时间t s的关系式为 ( )
C. d=2×3×10 tD. d=3×10 t
5.[2023·湖北潜江]如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y 表示铁桶中的水面高度,y 表示水池中的水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y ,y 随时间t变化的函数图象大致为 ( )
6.[2024·河北]在平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.例如,将“和点”P(2,1)按上述规则连续平移3次后,得到点P (2, 2), 其 平 移 过 程 如 下:P(2,1) 有P (3,1) 上 ,P (3,2) 左,P (2,2)
余0 余1 余2
若将“和点”Q按上述规则连续平移16次后,得到点Q (-1,9),则点Q的坐标为 ( )
A.(6,1)或(7,1)
B.(15,-7)或(8,0)
C.(6,0)或(8,0)
D.(5,1)或(7,1)
7.[2023·内蒙古呼伦贝尔]将矩形纸板剪掉一个小矩形后剩余部分如图1所示,动点 P 从点A 出发,沿路径A→B→C→D→E→F匀速运动,速度为1 cm/s,点P 到达点 F 后停止运动,△APF 的面积S(cm )(S≠0)与点 P 的运动时间t(s)的关系如图2所示,根据图象获取了以下的信息:
①AF=5cm ;②a=6;③点 P 从点 E 运动到点 F 需要10 s;④矩形纸板裁剪前与裁剪后的周长均为34 cm.
其中正确的信息有 ( )
A.4个 B.3个 C.2个 D.1个
8.[2024·山东滨州]若函数 的解析式在实数范围内有意义,则自变量x的取值范围是 .
9.[2023·浙江衢州]在如图所示的方格纸上建立适当的平面直角坐标系,若点 A的坐标为(0,1),点 B 的坐标为(2,2),则点C的坐标为 .
10.[2023·江苏连云港]画一条水平数轴,以原点O为圆心,过数轴上的每一刻度点画同心圆,过原点O按逆时针方向依次画出与正半轴的夹角度数分别为30°,60°,90°,120°,…,330°的射线,这样就建立了“圆”坐标系.如图,在建立的“圆”坐标系内,我们可以将点 A,B,C的坐标分别表示为A(6,60°),B(5,180°),C(4,330°),则点 D 的坐标可以表示为 .
11.[2023·黑龙江齐齐哈尔]如图,在平面直角坐标系中,点A 在y轴上,点B在x轴上,OA=OB=4,连接AB,过点O作 OA ⊥AB 于点 A ,过点 A 作A B ⊥x轴于点 B ;过点 B 作 B A ⊥AB于点A ,过点 A 作A B ⊥x轴于点B ;过点 B 作 B A ⊥AB于点A ,过点 A 作 A B ⊥x轴于点B ……按照规律操作下去,则点 A 的坐标为
1. A ∵点A(1,2)的横坐标和纵坐标均为正数,∴点A(1,2)在第一象限.
2. D 观察题图,当t=3时,h=13,∴这只蝴蝶飞行的最高高度约为13 m.
3. D ∵a+b>0, ab>0,∴a>0,b>0,∴(a,b)在第一象限,(-a,b)在第二象限,(-a,-b)在第三象限,(a,-b)在第四象限.
4. A 激光由L到M的时间为 光速为 则L到M的距离
5. C 根据题意,先用水管往铁桶中持续匀速注水,∴y 从0开始,高度与注水时间成正比,当到达t 时,铁桶中注满水,∴高度开始不变.
0到 t ,长方体水池中没有水,∴y 高度为0.
t 到t ,开始注水,∴y 从O开始.
∵铁桶底面积小于水池底面积的一半,
∴y 比y 增长得慢,即倾斜程度低.
t 到t ,底面积为长方体的底面积,
∴y 增长得更慢,即倾斜程度更低.
∵注水直到长方体水池有水溢出一会儿为止,
∴t 到t ,y 的值不变.
6. D 由题意,可得点 P (2,2)横、纵坐标之和除以3所得的余数为1,继而向上平移1个单位长度得到点 P (2,3),此时横、纵坐标之和除以3所得的余数为2,继而向左平移1个单位长度得到点P (1,3),此时横、纵坐标之和除以3所得的余数为1,又向上平移1个单位长度……因此发现规律为若“和点”横、纵坐标之和除以 3 所得的余数为0时,先向右平移1个单位长度,再按照向上、向左、向上、向左不断重复的规律平移.
若“和点”Q按上述规则连续平移16次后,得到点Q (-1,9),则按照“和点” Q 反向运动16次即可求出点 Q的坐标,可以分为两种情况:
①若点 Q 先向右平移1 个单位长度得到点Q (0,9),此时横、纵坐标之和除以3所得的余数为0,应该是点 Q 向右平移1个单位长度得到点Q ,故不符合题意,舍去;②若点 Q 先向下平移1个单位长度得到点Q (-1,8),此时横、纵坐标之和除以3所得的余数为1,则应该向上平移1个单位长度得到点 Q ,故符合题意.
∴点 Q 先向下平移,再向右平移,当平移了15次后,共计向下平移了8次,向右平移了7次,此时坐标为(-1+7,9-8),即(6,1),
∴最后一次若向左平移,则点 Q的坐标为(5,1),若向右平移,则点 Q的坐标为(7,1).
7. C 由题图可知,当点 P 运动到点 B 时,△PAF的面积是5 cm ,AB=2cm,
∴AF=5cm,故①正确;
由题图可知,当点 P运动到点D 时,△PAF的面积是25 cm ,∴ AF·EF=25,∴EF=10 cm,∴10÷1=10(s),故③正确;
由题意,易得当点 P从点C运动到点 D 时,用时8s,BC段运动时长为13-10=3(s),a=2+3=5,故②错误;
DE=AF+BC=5+3=8(cm),EF=10 cm,裁剪前周长为(8+10)×2=36(cm),故④错误.
8. x≠1 ∵函数 的解析式在实数范围内有意义,
∴x-1≠0,∴x≠1.
9.(1,3) 由点 A 的坐标为(0,1),点 B 的坐标为(2,2),可确定原点位置和坐标系如图所示.
由图可得,点C的坐标为(1,3).
10.(3,150°) ∵点 D 与圆心的距离为3,射线OD与x轴正半轴的夹角度数为150°,∴点 D 的坐标可以表示为(3,150°).
在平面直角坐标系中,点A在y轴上,点B在x轴上,OA=OB=4,
∴△OAB 是等腰直角三角形,∠OBA=45°.
∵OA ⊥AB,∴△OA B 是等腰直角三角形.
同理可得,△OA B ,△A B B均为等腰直角三角形,∴A (2,2).
根据题图中所有的三角形均为等腰直角三角形,依次可得
由此可推出点 A 的坐标为
1.[2023·江苏盐城]在平面直角坐标系中,点A(1,2)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.[2022·重庆 A 卷]如图,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间t(s)的变化情况,则这只蝴蝶飞行的最高高度约为 ( )
A.5m B.7m C.10m D.13m
3.[2023·黑龙江大庆]已知a+b>0, ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是 ( )
A.(a,b) B.(-a,b)
C.(-a,-b) D.(a,-b)
4.[2024·广西]激光测距仪L 发出的激光束以3×10 km/s的速度射向目标M,ts后测距仪L收到M 反射回的激光束,则L到M 的距离d km与时间t s的关系式为 ( )
C. d=2×3×10 tD. d=3×10 t
5.[2023·湖北潜江]如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y 表示铁桶中的水面高度,y 表示水池中的水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y ,y 随时间t变化的函数图象大致为 ( )
6.[2024·河北]在平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.例如,将“和点”P(2,1)按上述规则连续平移3次后,得到点P (2, 2), 其 平 移 过 程 如 下:P(2,1) 有P (3,1) 上 ,P (3,2) 左,P (2,2)
余0 余1 余2
若将“和点”Q按上述规则连续平移16次后,得到点Q (-1,9),则点Q的坐标为 ( )
A.(6,1)或(7,1)
B.(15,-7)或(8,0)
C.(6,0)或(8,0)
D.(5,1)或(7,1)
7.[2023·内蒙古呼伦贝尔]将矩形纸板剪掉一个小矩形后剩余部分如图1所示,动点 P 从点A 出发,沿路径A→B→C→D→E→F匀速运动,速度为1 cm/s,点P 到达点 F 后停止运动,△APF 的面积S(cm )(S≠0)与点 P 的运动时间t(s)的关系如图2所示,根据图象获取了以下的信息:
①AF=5cm ;②a=6;③点 P 从点 E 运动到点 F 需要10 s;④矩形纸板裁剪前与裁剪后的周长均为34 cm.
其中正确的信息有 ( )
A.4个 B.3个 C.2个 D.1个
8.[2024·山东滨州]若函数 的解析式在实数范围内有意义,则自变量x的取值范围是 .
9.[2023·浙江衢州]在如图所示的方格纸上建立适当的平面直角坐标系,若点 A的坐标为(0,1),点 B 的坐标为(2,2),则点C的坐标为 .
10.[2023·江苏连云港]画一条水平数轴,以原点O为圆心,过数轴上的每一刻度点画同心圆,过原点O按逆时针方向依次画出与正半轴的夹角度数分别为30°,60°,90°,120°,…,330°的射线,这样就建立了“圆”坐标系.如图,在建立的“圆”坐标系内,我们可以将点 A,B,C的坐标分别表示为A(6,60°),B(5,180°),C(4,330°),则点 D 的坐标可以表示为 .
11.[2023·黑龙江齐齐哈尔]如图,在平面直角坐标系中,点A 在y轴上,点B在x轴上,OA=OB=4,连接AB,过点O作 OA ⊥AB 于点 A ,过点 A 作A B ⊥x轴于点 B ;过点 B 作 B A ⊥AB于点A ,过点 A 作A B ⊥x轴于点B ;过点 B 作 B A ⊥AB于点A ,过点 A 作 A B ⊥x轴于点B ……按照规律操作下去,则点 A 的坐标为
1. A ∵点A(1,2)的横坐标和纵坐标均为正数,∴点A(1,2)在第一象限.
2. D 观察题图,当t=3时,h=13,∴这只蝴蝶飞行的最高高度约为13 m.
3. D ∵a+b>0, ab>0,∴a>0,b>0,∴(a,b)在第一象限,(-a,b)在第二象限,(-a,-b)在第三象限,(a,-b)在第四象限.
4. A 激光由L到M的时间为 光速为 则L到M的距离
5. C 根据题意,先用水管往铁桶中持续匀速注水,∴y 从0开始,高度与注水时间成正比,当到达t 时,铁桶中注满水,∴高度开始不变.
0到 t ,长方体水池中没有水,∴y 高度为0.
t 到t ,开始注水,∴y 从O开始.
∵铁桶底面积小于水池底面积的一半,
∴y 比y 增长得慢,即倾斜程度低.
t 到t ,底面积为长方体的底面积,
∴y 增长得更慢,即倾斜程度更低.
∵注水直到长方体水池有水溢出一会儿为止,
∴t 到t ,y 的值不变.
6. D 由题意,可得点 P (2,2)横、纵坐标之和除以3所得的余数为1,继而向上平移1个单位长度得到点 P (2,3),此时横、纵坐标之和除以3所得的余数为2,继而向左平移1个单位长度得到点P (1,3),此时横、纵坐标之和除以3所得的余数为1,又向上平移1个单位长度……因此发现规律为若“和点”横、纵坐标之和除以 3 所得的余数为0时,先向右平移1个单位长度,再按照向上、向左、向上、向左不断重复的规律平移.
若“和点”Q按上述规则连续平移16次后,得到点Q (-1,9),则按照“和点” Q 反向运动16次即可求出点 Q的坐标,可以分为两种情况:
①若点 Q 先向右平移1 个单位长度得到点Q (0,9),此时横、纵坐标之和除以3所得的余数为0,应该是点 Q 向右平移1个单位长度得到点Q ,故不符合题意,舍去;②若点 Q 先向下平移1个单位长度得到点Q (-1,8),此时横、纵坐标之和除以3所得的余数为1,则应该向上平移1个单位长度得到点 Q ,故符合题意.
∴点 Q 先向下平移,再向右平移,当平移了15次后,共计向下平移了8次,向右平移了7次,此时坐标为(-1+7,9-8),即(6,1),
∴最后一次若向左平移,则点 Q的坐标为(5,1),若向右平移,则点 Q的坐标为(7,1).
7. C 由题图可知,当点 P 运动到点 B 时,△PAF的面积是5 cm ,AB=2cm,
∴AF=5cm,故①正确;
由题图可知,当点 P运动到点D 时,△PAF的面积是25 cm ,∴ AF·EF=25,∴EF=10 cm,∴10÷1=10(s),故③正确;
由题意,易得当点 P从点C运动到点 D 时,用时8s,BC段运动时长为13-10=3(s),a=2+3=5,故②错误;
DE=AF+BC=5+3=8(cm),EF=10 cm,裁剪前周长为(8+10)×2=36(cm),故④错误.
8. x≠1 ∵函数 的解析式在实数范围内有意义,
∴x-1≠0,∴x≠1.
9.(1,3) 由点 A 的坐标为(0,1),点 B 的坐标为(2,2),可确定原点位置和坐标系如图所示.
由图可得,点C的坐标为(1,3).
10.(3,150°) ∵点 D 与圆心的距离为3,射线OD与x轴正半轴的夹角度数为150°,∴点 D 的坐标可以表示为(3,150°).
在平面直角坐标系中,点A在y轴上,点B在x轴上,OA=OB=4,
∴△OAB 是等腰直角三角形,∠OBA=45°.
∵OA ⊥AB,∴△OA B 是等腰直角三角形.
同理可得,△OA B ,△A B B均为等腰直角三角形,∴A (2,2).
根据题图中所有的三角形均为等腰直角三角形,依次可得
由此可推出点 A 的坐标为
同课章节目录
