2009-2010学年苏教版必修2期末数学复习试题及答案
文档属性
| 名称 | 2009-2010学年苏教版必修2期末数学复习试题及答案 |  | |
| 格式 | rar | ||
| 文件大小 | 38.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-16 22:38:00 | ||
图片预览



文档简介
09-10 学年高一上学期末数学必修2复习测试题
第一部分 选择题(共50分)
选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.分别与两条异面直线同时相交的直线( )。
(A)一定是异面直线 (B)不可能平行
(C)不可能相交 (D)相交、平行、异面都有可能
2.若一条直线和一个平面平行,夹在直线和平面间的两条线段相等,那么这两条线段的位置关系是( )
(A)平行 (B)相交 (C)异面 (D)相交、平行或异面
3.已知直线a,b,c及平面α,则它们具备以下哪一条件时,a∥b成立( )
(A)a ∥α且b∥α (B)a⊥c 且b⊥c
(C)a、b与α成等角 (D)a∥c且b∥c
4.平面α、β及直线l满足:α⊥β,l∥α,则一定有( )
(A)l∥β (B)l β (C)l与β相交 (D)l∥β或lβ或l与β相交
5.将一个直角梯形绕其较短的底所在的直线旋转一周得到一个几何体。关于几何体的下列描述中,正确的是( )
(A)是一个圆台 (B)是一个圆柱
(C)是一个圆台和一个圆锥的简单组合体
(D)是一个圆柱被挖去一个圆锥后所剩的几何体
6.方程x2+y2-x+y+m=0表示一个圆,则m的取值范围是( )
(A)m≤2 (B)m<2 (C)m< (D)m≤
7.设直线ax+by+c=0的倾斜角为α,且cosα+sinα=0,则a、b满足( )
(A)a-b=0 (B)a-b=1 (C)a+b=1 (D)a+b=0
8.如图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积是( )
(A) 6+ (B) 24+ (C) 24+2 (D) 32
9.若y=a|x|的图象与直线y=x+a(a>0)有两个不同的交点,则a的取值范围是( )
(A)01 (C)a>0且a≠1 (D)a=1
10.若直线ax+by=1与圆x2+y2=1有两个公共点,则点P(a,b)与圆的位置关系是( )
(A)在圆外 (B)在圆内 (C)在圆上 (D)以上皆有可能
第二部分 非选择题(共100分)
二、填空题:本大题共4小题,每小题5分,共20分。
11.直线l是平面α的一条斜线,则过l和平面α垂直的平面有___________个。
12.在Rt△ABC中,D是斜边AB的中点,AC=6,BC=8,EC⊥平面ABC且EC=12,则ED=_______________。
13.等腰梯形ABCD上底边CD=1,腰AD=CB=,底边AB=3,按平行于上、下底边取x轴,则直观图A’B’C’D’的面积为_______________。
14.若经过点P(-1,0)的直线与圆x2+y2+4x-2y+3=0相切,则此直线在y轴上的截距是______________。
三、解答题:本大题共6小题,共80分。解答应写出文字说明、演算步骤或推证过程。
15.(12分)已知长方体的全面积为11,十二条棱长之和为24,求这个长方体的对角线的长。
16.(满分12分)求斜率为且与坐标轴所围成的三角形的周长为12的直线方程。
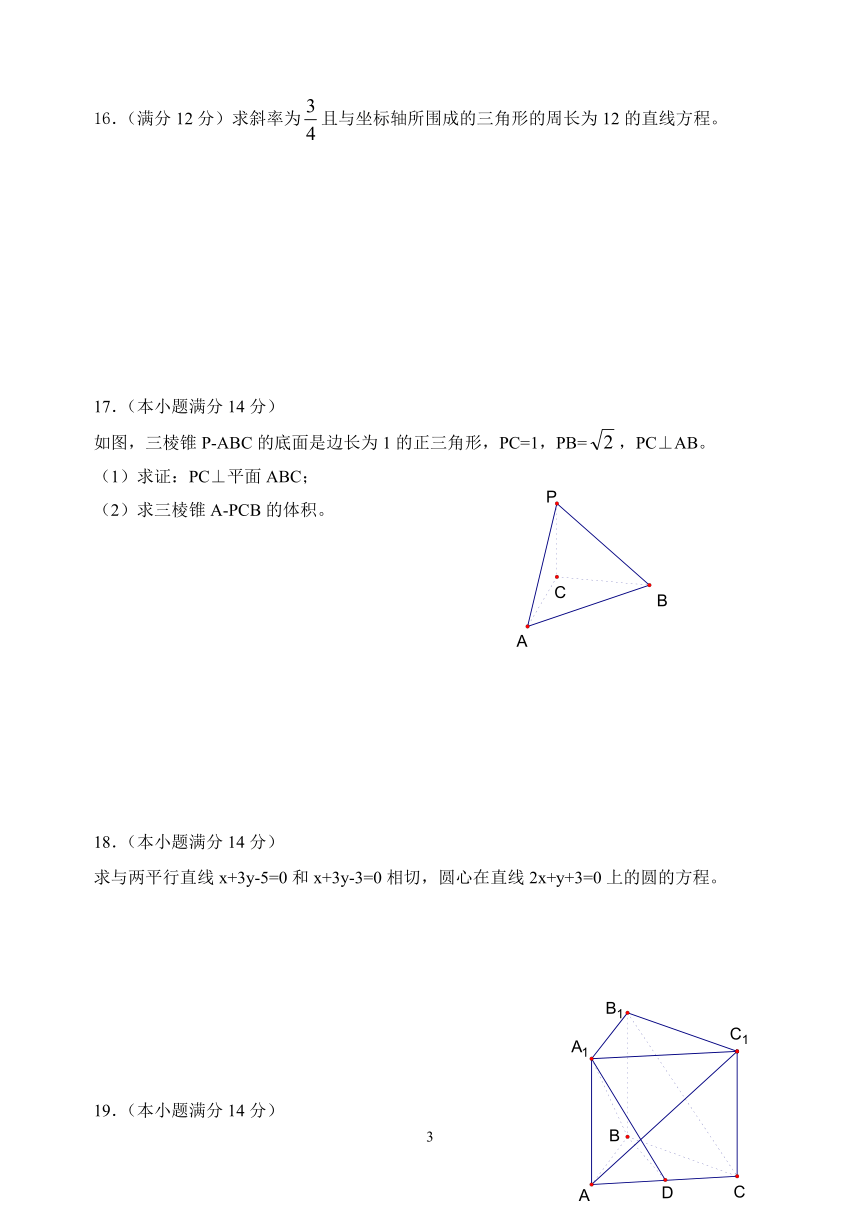
17.(本小题满分14分)
如图,三棱锥P-ABC的底面是边长为1的正三角形,PC=1,PB=,PC⊥AB。
(1)求证:PC⊥平面ABC;
(2)求三棱锥A-PCB的体积。
18.(本小题满分14分)
求与两平行直线x+3y-5=0和x+3y-3=0相切,圆心在直线2x+y+3=0上的圆的方程。
19.(本小题满分14分)
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,D为AC的中点。
(1)求证:B1C∥平面A1BD;
(2)若AC1⊥平面A1BD,求证 :B1C1⊥平面ABB1A1。
20.(本小题满分14分)
已知圆C:x2+y2-2x-2y+1=0,直线l:y=kx且l与圆C交于P、Q两点。点M(0,b)且MP⊥MQ。
当b=1时,求k的值;
当b∈(1,)时,求k的取值范围。
09-10 学年高二上学期末数学必修2复习测试题答卷
一、【选择题:每小题5分,共50分】
1
2
3
4
5
6
7
8
9
10
【填空题:每小题5分,共20分】
11、 12、
13、 14、
三、【解答题:6小题,共80分】
15.
16.
17.
18.
19.
20.
09-10 学年高二上学期末数学必修2复习测试题答案
一、【选择题:每小题5分,共50分】
1
2
3
4
5
6
7
8
9
10
B
D
D
D
D
C
A
C
B
A
【填空题:每小题5分,共20分】
11、 1 ;12、 13 ;13、;14、 1
三、【解答题:6小题,共80分】
15. 解:设此长方体同一顶点处的三条棱长分别为a、b、c。则
∴长方体对角线长为=5……12分
16.解:设直线方程为y=x+b
令x=0,得y=b;令y=0,得x= -b …………….…4分
由题意得:|b|+|-b|+=12 …..….…8分
解得b=3或-3
∴所求直线方程为y=x±3,即3x-4y±12=0 ……12分
17.(1)证明:由题意△PBC中,
∴PC⊥BC ………………………………….4分
又∵PC⊥AB,BC∩AB=B
∴PC⊥面ABC …………………………….8分
(2)解:由(1)知:PC是三棱锥P-ABC的高
∴VA-PCB= VP-ABC= S△ABC ·PC=××1=…………14分
18.
解:设所求圆的方程为(x-a)2+(y-b)2=r2
由已知,两平行线间的距离为d=
∴r=∴圆心(a,b)到直线x+3y-5=0和x+3y-3=0的距离都是
∴…………………….8分
又∵圆心在直线2x+y+3=0上,∴2a+b+3=0,与|a+3b-5|=1联立
解得,…………………….12分
但当时,不满足|a+3b-3|=1 ∴仅符合。
此时所求圆的方程为(x+)2+(y-)2= …………………14分
19.
(1)证明:取A1C1中点E,连接B1E、CE、DE。
由直三棱柱ABC-A1B1C1知A1E∥DC且A1E=DC
∴A1ECD为平行四边形 ∴CE∥A1D ………….3分
同理,B1E∥BD
又∵B1E∩EC=E,A1D∩BD=D
∴ 平面EB1C∥平面A1BD
∵B1C平面EB1C
∴B1C∥平面A1BD………………….………6分
(2)证明:由直三棱柱ABC-A1B1C1知ABB1A1为矩形
又AB=BB1,∴ABB1A1为正方形……………9分
连接AB1,则AB1⊥A1B
∵AC1⊥平面A1BD
∴AC1⊥A1B 又AB1∩AC1=A
∴A1B⊥平面AB1C1 ………………………….12分
∴A1B⊥B1C1 又BB1⊥B1C1 且 A1B∩BB1=B
∴B1C1⊥平面ABB1A1………………………14分
20.
解:(1)当b=1时,M(0,1)
∵圆心C(1,1) ∴若MP⊥MQ,则直线PQ必过圆心C
∴1=k×1 解得k=1为所求。…………………………..……….6分
(2)当b∈(1,)时,联立
消去y,整理得(1+k2)x2-2(1+k)x+1=0 …………………...8分
设P(x1,y1)、Q(x2,y2),则 (*)
∵MP⊥MQ,∴kMPkMQ=-1
∴x1x2+(y1-b)(y2-b)=0
将(*)及y1=kx1,y2=kx2代入上式,整理得
(1+k2)b2-2k(1+k)b+(1+k2)=0……………..….…….10分
由△>0得k>0;当b=1时,k=1。
令f(b)=(1+k2)b2-2k(1+k)b+(1+k2) (b∈(1,))
则:b∈(1,)时,f(b)=0有解b1、b2,则b1b2=1。
∴f(b)=0的一根小于1,另一根在(1,)上………………12分
∴
解上式得k的取值范围为(1,6-)∪(6+,+∞)……14分
第一部分 选择题(共50分)
选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.分别与两条异面直线同时相交的直线( )。
(A)一定是异面直线 (B)不可能平行
(C)不可能相交 (D)相交、平行、异面都有可能
2.若一条直线和一个平面平行,夹在直线和平面间的两条线段相等,那么这两条线段的位置关系是( )
(A)平行 (B)相交 (C)异面 (D)相交、平行或异面
3.已知直线a,b,c及平面α,则它们具备以下哪一条件时,a∥b成立( )
(A)a ∥α且b∥α (B)a⊥c 且b⊥c
(C)a、b与α成等角 (D)a∥c且b∥c
4.平面α、β及直线l满足:α⊥β,l∥α,则一定有( )
(A)l∥β (B)l β (C)l与β相交 (D)l∥β或lβ或l与β相交
5.将一个直角梯形绕其较短的底所在的直线旋转一周得到一个几何体。关于几何体的下列描述中,正确的是( )
(A)是一个圆台 (B)是一个圆柱
(C)是一个圆台和一个圆锥的简单组合体
(D)是一个圆柱被挖去一个圆锥后所剩的几何体
6.方程x2+y2-x+y+m=0表示一个圆,则m的取值范围是( )
(A)m≤2 (B)m<2 (C)m< (D)m≤
7.设直线ax+by+c=0的倾斜角为α,且cosα+sinα=0,则a、b满足( )
(A)a-b=0 (B)a-b=1 (C)a+b=1 (D)a+b=0
8.如图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积是( )
(A) 6+ (B) 24+ (C) 24+2 (D) 32
9.若y=a|x|的图象与直线y=x+a(a>0)有两个不同的交点,则a的取值范围是( )
(A)0
10.若直线ax+by=1与圆x2+y2=1有两个公共点,则点P(a,b)与圆的位置关系是( )
(A)在圆外 (B)在圆内 (C)在圆上 (D)以上皆有可能
第二部分 非选择题(共100分)
二、填空题:本大题共4小题,每小题5分,共20分。
11.直线l是平面α的一条斜线,则过l和平面α垂直的平面有___________个。
12.在Rt△ABC中,D是斜边AB的中点,AC=6,BC=8,EC⊥平面ABC且EC=12,则ED=_______________。
13.等腰梯形ABCD上底边CD=1,腰AD=CB=,底边AB=3,按平行于上、下底边取x轴,则直观图A’B’C’D’的面积为_______________。
14.若经过点P(-1,0)的直线与圆x2+y2+4x-2y+3=0相切,则此直线在y轴上的截距是______________。
三、解答题:本大题共6小题,共80分。解答应写出文字说明、演算步骤或推证过程。
15.(12分)已知长方体的全面积为11,十二条棱长之和为24,求这个长方体的对角线的长。
16.(满分12分)求斜率为且与坐标轴所围成的三角形的周长为12的直线方程。
17.(本小题满分14分)
如图,三棱锥P-ABC的底面是边长为1的正三角形,PC=1,PB=,PC⊥AB。
(1)求证:PC⊥平面ABC;
(2)求三棱锥A-PCB的体积。
18.(本小题满分14分)
求与两平行直线x+3y-5=0和x+3y-3=0相切,圆心在直线2x+y+3=0上的圆的方程。
19.(本小题满分14分)
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,D为AC的中点。
(1)求证:B1C∥平面A1BD;
(2)若AC1⊥平面A1BD,求证 :B1C1⊥平面ABB1A1。
20.(本小题满分14分)
已知圆C:x2+y2-2x-2y+1=0,直线l:y=kx且l与圆C交于P、Q两点。点M(0,b)且MP⊥MQ。
当b=1时,求k的值;
当b∈(1,)时,求k的取值范围。
09-10 学年高二上学期末数学必修2复习测试题答卷
一、【选择题:每小题5分,共50分】
1
2
3
4
5
6
7
8
9
10
【填空题:每小题5分,共20分】
11、 12、
13、 14、
三、【解答题:6小题,共80分】
15.
16.
17.
18.
19.
20.
09-10 学年高二上学期末数学必修2复习测试题答案
一、【选择题:每小题5分,共50分】
1
2
3
4
5
6
7
8
9
10
B
D
D
D
D
C
A
C
B
A
【填空题:每小题5分,共20分】
11、 1 ;12、 13 ;13、;14、 1
三、【解答题:6小题,共80分】
15. 解:设此长方体同一顶点处的三条棱长分别为a、b、c。则
∴长方体对角线长为=5……12分
16.解:设直线方程为y=x+b
令x=0,得y=b;令y=0,得x= -b …………….…4分
由题意得:|b|+|-b|+=12 …..….…8分
解得b=3或-3
∴所求直线方程为y=x±3,即3x-4y±12=0 ……12分
17.(1)证明:由题意△PBC中,
∴PC⊥BC ………………………………….4分
又∵PC⊥AB,BC∩AB=B
∴PC⊥面ABC …………………………….8分
(2)解:由(1)知:PC是三棱锥P-ABC的高
∴VA-PCB= VP-ABC= S△ABC ·PC=××1=…………14分
18.
解:设所求圆的方程为(x-a)2+(y-b)2=r2
由已知,两平行线间的距离为d=
∴r=∴圆心(a,b)到直线x+3y-5=0和x+3y-3=0的距离都是
∴…………………….8分
又∵圆心在直线2x+y+3=0上,∴2a+b+3=0,与|a+3b-5|=1联立
解得,…………………….12分
但当时,不满足|a+3b-3|=1 ∴仅符合。
此时所求圆的方程为(x+)2+(y-)2= …………………14分
19.
(1)证明:取A1C1中点E,连接B1E、CE、DE。
由直三棱柱ABC-A1B1C1知A1E∥DC且A1E=DC
∴A1ECD为平行四边形 ∴CE∥A1D ………….3分
同理,B1E∥BD
又∵B1E∩EC=E,A1D∩BD=D
∴ 平面EB1C∥平面A1BD
∵B1C平面EB1C
∴B1C∥平面A1BD………………….………6分
(2)证明:由直三棱柱ABC-A1B1C1知ABB1A1为矩形
又AB=BB1,∴ABB1A1为正方形……………9分
连接AB1,则AB1⊥A1B
∵AC1⊥平面A1BD
∴AC1⊥A1B 又AB1∩AC1=A
∴A1B⊥平面AB1C1 ………………………….12分
∴A1B⊥B1C1 又BB1⊥B1C1 且 A1B∩BB1=B
∴B1C1⊥平面ABB1A1………………………14分
20.
解:(1)当b=1时,M(0,1)
∵圆心C(1,1) ∴若MP⊥MQ,则直线PQ必过圆心C
∴1=k×1 解得k=1为所求。…………………………..……….6分
(2)当b∈(1,)时,联立
消去y,整理得(1+k2)x2-2(1+k)x+1=0 …………………...8分
设P(x1,y1)、Q(x2,y2),则 (*)
∵MP⊥MQ,∴kMPkMQ=-1
∴x1x2+(y1-b)(y2-b)=0
将(*)及y1=kx1,y2=kx2代入上式,整理得
(1+k2)b2-2k(1+k)b+(1+k2)=0……………..….…….10分
由△>0得k>0;当b=1时,k=1。
令f(b)=(1+k2)b2-2k(1+k)b+(1+k2) (b∈(1,))
则:b∈(1,)时,f(b)=0有解b1、b2,则b1b2=1。
∴f(b)=0的一根小于1,另一根在(1,)上………………12分
∴
解上式得k的取值范围为(1,6-)∪(6+,+∞)……14分
同课章节目录
