福建省龙岩第一中学2024-2025学年高一下学期第二次月考数学试卷(图片版,含答案)
文档属性
| 名称 | 福建省龙岩第一中学2024-2025学年高一下学期第二次月考数学试卷(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 541.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 09:36:45 | ||
图片预览



文档简介
龙岩一中2024-2025 学年下学期高一数学第二次月考试卷
考试时间:120 分钟,共 150 分
一、单选题(本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
2
1.已知复数 z = ,则( )
1+ i
A. z 的实部为 -1 B. z 的虚部为 i
C. z = 2 D. z =1- i
2.已知一组数据为 20,30,40,50,50,60,70,80,其平均数、第 60 百分位数和众数的大小关系是( )
A.平均数>第 60 百分位数>众数 B.平均数<第 60 百分位数<众数
C.第 60 百分位数<众数<平均数 D.平均数=第 60 百分位数=众数
r r r r r r r r r r
3.已知向量a ,b 满足 a - b = a ×b = 2, a - b = 10 ,则 cos a,b = ( )
2 2 4
A. B 1. 2 C. D.5 3 5
π
4.已知VABC 的内角A , B ,C 的对边分别为 a,b , c, A = ,b = 4 ,下面使得VABC 有两组解的 a的值可以为
3
( )
A.3 B. 13 C.2 D.3 3
5.设 m,n 是两条不同的直线,a , b 是两个不同的平面,给出下列说法,其中正确的是( )
A.若m / /a ,n ^ b ,m ^ n ,则a ^ b
B.若m / /a ,m ^ b ,则a ^ b
C.若m ^ n, m a , n b ,则a ^ b
D.若m ^ a , n b , m ^ n,则a ^ b
6.如图,VA O B 是由斜二测画法得到的VAOB 水平放置的直观图,其中O A = O B = 2 ,点C 为线段 A B 的中点,C
对应原图中的点C ,则在原图中下列说法正确的是( )
uuur uuur
A.OC × AB = 0 B.VAOB 的面积为 2
uuur uuur uuur uuur 5 uuurC.OC 在OB上的投影向量为 2OB D.与 AB 同向的单位向量为 AB
10
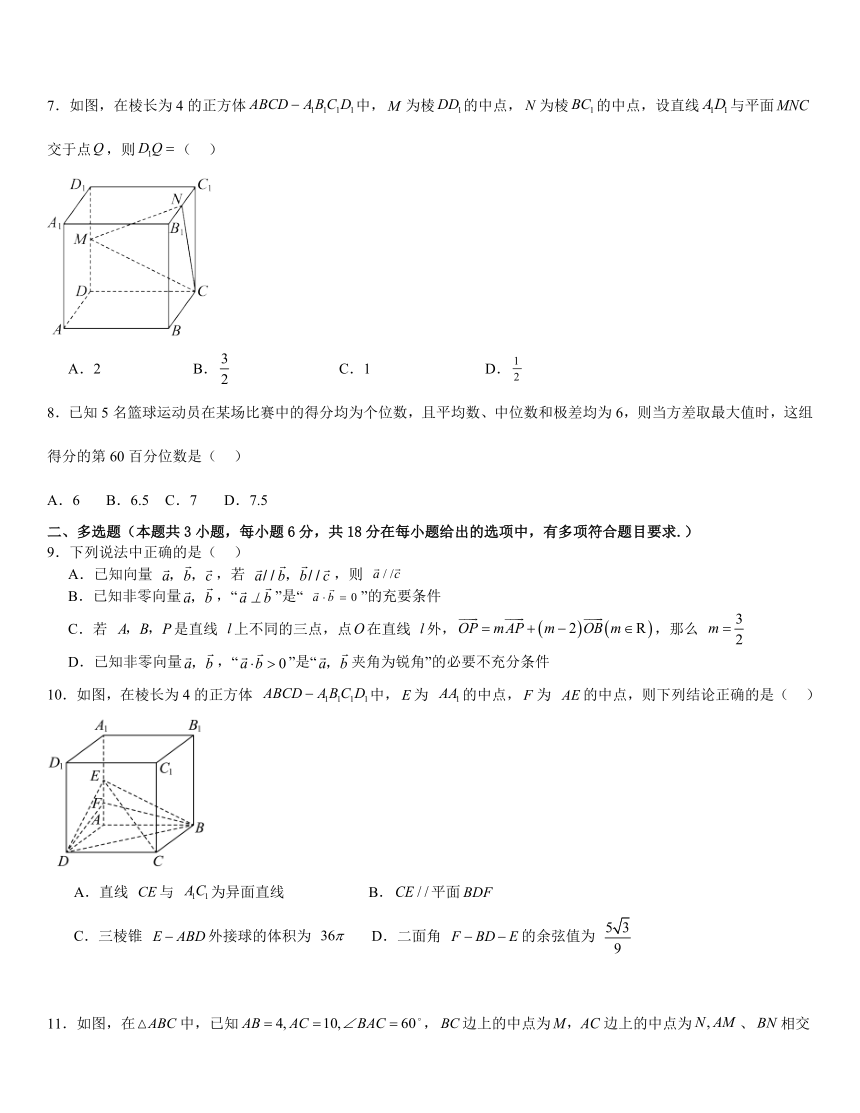
7.如图,在棱长为 4 的正方体 ABCD - A1B1C1D1中,M 为棱DD1的中点, N 为棱BC1的中点,设直线 A1D1与平面MNC
交于点Q,则D1Q =( )
3
A.2 B. C.1 D 1.
2 2
8.已知 5 名篮球运动员在某场比赛中的得分均为个位数,且平均数、中位数和极差均为 6,则当方差取最大值时,这组
得分的第 60 百分位数是( )
A.6 B.6.5 C.7 D.7.5
二、多选题(本题共 3 小题,每小题 6 分,共 18 分在每小题给出的选项中,有多项符合题目要求.)
9.下列说法中正确的是(
r )r r r rA r.已知向量 a,b,c ,若 ar/ / b,b / / cr ,则 a / /cr
B r
r r r
.已知非零向量 a,b “ ar, ^ b ” “ ar是 × b = 0 ”的充要条件
uuur uuur uuur
C.若 A,B,P是直线 l上不同的三点,点O在直线 l外,OP = mAP + m - 2 OB m R m 3,那么 =
2
r r r rD.已知非零向量 a,b r,“ a ×b > 0 ”是“ ar,b 夹角为锐角”的必要不充分条件
10.如图,在棱长为 4 的正方体 ABCD - A1B1C1D1中,E 为 AA1的中点,F 为 AE 的中点,则下列结论正确的是( )
A.直线 CE与 A1C1为异面直线 B.CE / /平面BDF
C.三棱锥 E - ABD外接球的体积为 36p D 5 3.二面角 F - BD - E 的余弦值为
9
11.如图,在VABC 中,已知 AB = 4, AC =10, BAC = 60 o,BC 边上的中点为M,AC 边上的中点为 N , AM 、BN 相交
于点 P ,则下列结论正确的是( )
A BC 2 19 B VABC 7 - 19. = . 的内切圆的半径为
3
uuuur uuur
C 4 91. AM 与BN 夹角的余弦值为
91
uuur uuur é 16 ù
D.过点 P 作直线交线段 AB 和BC 于点EF ,则BE × BF 的取值范围是 ê-2, - 9 ú
三、填空题(本题共 3 小题,每小题 5 分,共 15 分.)
12.某学校师生共有 3000 人,现用分层抽样方法抽取一个容量为 225 的样本,已知样本中教师人数为 15 人,则该校学
生人数为 .
13.在直三棱柱 ABC - A1B1C1中,AC ^ BC ,AC = BC = AA1 = 2,动点 P 在棱 B1C1 上,则点 P 到平面 A1BC 的距离为 .
14.在VABC 中, AB = 2AC, D 为边BC 的中点, A的平分线交BC 于点E ,若VADE 的面积为 1,则VABC 的面积
为 ,DE 的最小值为 .
四、解答题(本题共 5 小题,共 77 分,解答应写出文字说明、证明过程或演算步骤.)
15.已知 z
z 1 m
是复数, z + 2i 和 均为实数, z1 = z + - i,其中 i是虚数单位.1- i m m -1
(1)求复数 z 的共轭复数 z ;
(2)若复数 z1 在复平面内对应的点在第一象限,求实数m 的取值范围.
16.随着老年人消费需求从“生存型”向“发展型”转变.消费层次不断提升,“银发经济”成为社会热门话题之一,被各企
业持续关注. 某企业为了解该地老年人消费能力情况,对该地年龄在 60,80 的老年人的年收入按年龄 60,70 , 70,80
分成两组进行分层抽样调查,已知抽取了年龄在 60,70 的老年人500人. 年龄在 70,80 的老年人300人.现作出年龄
在 60,70 的老年人年收入的频率分布直方图(如图所示):
(1)根据频率分布直方图,若每个区间取中点值为代表,估计该地年龄在 60,70 的老年人年收入的平均数及第 95百分位
数;
(2)已知年龄在 60,70 的老年人年收入的方差为3,年龄在 70,80 的老年人年收入的平均数和方差分别为3.75和1.4,试
估计年龄在 60,80 的老年人年收入的方差.
r
17.在VABC 中,角 A,B,C 的对边分别为 a,b,c ,且向量m = 3a - b,a - c nr, = sinA r r+ sinC,sinB ,m / /n .
(1)求角 C ;
(2)若 VABC 的面积为 3,sinB =1+ cosA,点D为边 AC 的中点,求BD的长.
18.如图,在正方形 ABCD 中,点 E,F 分别是 AB,CD 的中点.现将VADE 沿 DE 折起,得到四棱锥 A - BCDE .
(1)证明:BF // 平面 ADE;
(2)当VACD为等边三角形时,证明:平面 AEF ^ 平面 BCDE;
(3)在(2)的条件下,求二面角 A - DE - C 的余弦值.
19.如图,在三棱锥 A - BCD中,侧面 ABC 和底面BCD均为正三角形,且 AB = 2, AD = 3.
(1)求证:BC ^ AD ;
(2)已知 P 在棱 AD 上(不含端点)且 AP = l AD,
l 1(ⅰ)若 = ,求二面角P - BC - D 的大小;
2
3
(ⅱ)若直线 AC 与平面PBC 所成角的正弦值为 ,求实数l 的值.
4
龙岩一中2024-2025 学年下学期高一数学第二次月考参考答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C D A B B D C D BD BCD ACD
12.2800 13. 2 14. 6
2
2
z 2 2(1- i)1.C = = = 1- i ,则 z1 i (1 i)(1 i) 的实部为 1,虚部为-1, z = 2 , z =1+ i .+ + -
1
2.D 平均数为 20 + 30 + 40 + 50 + 50 + 60 + 70 + 80 = 50,Q8 60% = 4.8,\第 5 个数 50 即为第 60 百分位数.众数为
8
50,\它们的大小关系是平均数=第 60 百分位数=众数.
r r 2 r 2 r 2 r r r 2 r 2 r r 2 r 2 r 2 r r r r
3.A a - b = a + b - 2a ×b =10 ,\ a + b =14,Q a - b = a + b - 2 a b = 4,\ a b = 5,
r r r r
cos a,b ar ×b\ = r
2
=
a b 5 .
a b sin B bsin A sin B bsin A4.B 由题意,根据正弦定理有 = ,所以 = ,要使VABC 有两组解,则 = <1,且 a < b ,
sin A sin B a a
即bsin A
π
< a < b ,即 4sin < a < 4,即 2 3 < a < 4,所以选项所给四个数据中只有 13 符合,3
5.B 6.D
7.C 在平面CDD1C1 中,延长CM 交C1D1于 P,连接PN ,交 A1D1于 Q,在VPCC1中,D1M //CC1, D1M =
1 CC
2 1
,则
D1P=C1D1,
1 1
又在△PC1N 中,D1Q//NC1, D1P=C1D1,则D1Q= NC1 = B C =1 .2 4 1 1
8.D 因为这组得分的中位数和极差均为 6,可设这组得分从小到大分别为 a, x,6, y, a + 6 0 a 3 ,因为平均数为 6,可
得 x + y =18 - 2a又因为 x 6 , y a + 6,所以 x + y a +12,所以18 - 2a a +12,所以 a 2,故 2 a 3 .
当 a = 2时,这组得分分别为 2,6,6,8,8.方差:
(2 - 6)2 + (6 - 6)2 + (6 - 6)2 + (8 - 6)2 + (8 - 6)2 16 + 0 + 0 + 4 + 4 24
= = = 4.8
5 5 5
当 a = 3时,要使方差最大,则 x 取最小值 3, y 取最大值 9,这组得分分别为 3,3,6,9,9,
1
: [(3 - 6)2方差 + (3 - 6)2 + (6 - 6)2 + (9 - 6)2 + 9 36- 6)2 ù = = 7.2,此时方差最大.5 5
又由5 60% = 3,所以方差最大时的这组得分的第 60 百分位数是 6 和 9 的平均数 7.5.
9.BD 10.BCD
11 ACD A VABC AB 4 AC =10 1 16 +100 - BC
2
. 对于 ,在 中,且 = , ,由余弦定理得 = ,解得BC = 2 19 ,(负根舍去),
2 2 4 10
1 1
则 A 正确;对于 B,设VABC 的内切圆的半径为 r ,则 C
2 VABC
r = AB AC sin A,即C r = AB AC sin A,
2 VABC
即 (2 19 + 4 +10)r = 4 3 7 3 - 57 10 ,解得 r = ,故 B 错误;对于 C,如图所示,
2 3
以A 为原点,建立平面直角坐标系,易知 A(0,0),C(10,0),设B(x, y) ,
由两点间距离公式得 x2 + y2 =16, (x -10)2 + y2 = 76,解得 x = 2, y = 2 3 ,(负根舍去),
uuuur uuur uuuur uuur
故B(2, 2 3),由中点坐标公式得 N (5, 0) ,M (6, 3),故 AM = (6, 3) ,BN = (3, -2 3) ,设 AM 与BN 的夹角为q ,
故 cosq
18 - 6 12 4 91
= = =
39 21 91 ,故 C 正确;对于 D,易知由于BC 边上的中点为M ,AC 边上36 + ( 3)2 9 + (-2 3)2
BP 2 BE BF
的中点为 N ,而 P 是VABC 两条中线的交点,故 P 是VABC 的重心,所以 = ,设 = p, = q,
BN 3 BA BC
uuur
BP 2
uuur
BN 1
uuur uuur
(BA BC) 1 ( 1
uuur 1 uuur 1 1 1 1 1
= = + = BE + BF )
3 3 3 p q ,由于 P 在直线EF 上,所以
( + ) =1 + = 3
3 p q ,即 p q ,
1 1 2
0 < p 1,0 q 1< 1 1 = 3- 2 1 3 1 9 1 3 9而 ,所以 p , p q ,故得 - ÷ = - - ÷ ,p è p 4 è p 2 4
2 1 1 4 1 1 1
1 3 1 9 1 3 9 1
2 pq = = pq = =
- = - - -
= 2,所以 1 1 1 1 9 , 1 1 1 1 2 ,
p è p
÷ 4 p 2 ÷ è 4
è 2 ÷ ÷ 3- ÷ ÷ 3-è p q
÷
p è p è p q p è p
1
S BE BF sin ABC
故得 VBEF 2
p AB q BC pq 4 1= 1 = =
é , ùê ú,则SVABC sin ABC AB BC AB BC 9 2
2
BE BF pq BE BF
é ù 2 2 2
= = pq é 4 , 1 ùê ú BE
32 19
BF AB + BC - AC 19ê , 4 19 ú cos B = = - ,BA BC 4 2 19 9 2 9 2AB BC 38
uuur uuur uuur uuur 19 uuur uuur é32 19 ù uuur uuur uuur uuurBE × BF =| BE | × | BF | cos B = - | BE | × | BF |由于BE BF ê , 4 19 19,则9 ú BE × BF = - | BE | × | BF | [ 2,
16
- - ],
38 38 9
则 D 正确,
12.2800 13. 2
14. 6 2 在VABC 中,设 A, B,C 对应的边分别为 a,b,c,
2
a
因为D为BC 的中点,所以DC = .因为 AE 为 BAC 的平分线, AB = 2AC ,
2
AB BE
所以 = = 2, EC
BE a
= = ,所以DE = DC - EC
a 1
= ,因为 S
AC EC 2 3 6 VADE
= S =1,所以 S
6 VABC VABC
= 6 .
ì1 ì 2
24
bcsinA = 6,
b = ,
VABC 2 sinAí í a2 b2 c2 2bccosA
24 6 24cosA 30 - 24cosA
在 中, ,所以 ,因为 = + - = + - =
b = 2c c2 6= sinA sinA sinA sinA sinA
30 2 A 2 A sin + cos ÷ - 24 cos
2 A - sin2 A ÷
= è 2 2 è 2 2 A 3
A 1
A A = 27tan + A 18,当且仅当
tan = 时,等号成立,所以 a 3 2 ,所
2sin cos 2 tan 2 3
2 2 2
2
以DE .
2
15.(1)设 z = a + bi(a,b R),则 z + 2i = a + (b + 2)i ,Q z + 2i为实数,\b + 2 = 0 ,解得b = -2,………2 分
z a - 2i (a - 2i)(1+ i) a + 2 a - 2
\ = = = + i a - 2\ = 0
1- i 1- i (1+ i)(1- i) 2 2 为实数, ,解得 a = 2 ………4 分,2
\ z = 2 - 2i,\ z = 2 + 2i;………5 分
1 m 1 m 2m +1 3m - 2
(2)由(1)可知, z1 = z + - i = 2 + -
2 +
÷ i = - i,………8 分m m -1 m è m -1 m m -1
ì2m +1
> 0
Q复数 z
m
1 在复平面内对应的点在第一象限,\í 3m 2 ………10 分 -- > 0
m -1
2
< m <1 m
2
解得 ,故实数 的取值范围为 ,1÷ .……13 分3 è 3
16.(1)平均数为 2 0.04 + 3 0.08 + 4 0.18 + 5 0.26 + 6 0.20 + 7 0.15 + 8 0.05 + 9 0.04 = 5.35 .………3 分
而由于0.04 + 0.08 + 0.18 + 0.26 + 0.20 + 0.15 = 0.91< 0.95,
0.04 + 0.08 + 0.18 + 0.26 + 0.20 + 0.15 + 0.05 = 0.96 > 0.95,
故第95百分位数在区间第95百分位数内,设其为7.5 + x 0 < x <1 .
则0.04 + 0.08 + 0.18 + 0.26 + 0.20 + 0.15 + 0.05x = 0.95,得 x = 0.8 .
所以第95百分位数为7.5 + 0.8 = 8.3 .………7 分
(2)代入数值即知所求方差为
s 2 500 3+ 300 1.4 500 5.35
2 + 300 3.752 500 5.35 + 300 3.75
2
= + - = 3………15 分
500 + 300 500 + 300 è 500 + 300 ÷
r r
17.(1)因为 m // n,所以 3a - b sinB - a - c sinA + sinC = 0,由正弦定理得 a 2+ b 2- c 2= 3ab,
a2 + b2 - c2 3
由余弦定理得 cosC = = 因为C 0, π π,所以C = .………6 分
2ab 2 6
(2)因为 sinB 1 5π 3 1= + cosA,所以 sinB =1+ cos - B ÷ =1- cosB + sinB
1 3
,则 sinB + cosB =1
è 6 2 2 2 2
即 sin
B
π
+ ÷ =1 0 B
5π π B π 7π B π π< < < + < + = π,又 ,所以 ,则 ,所以 B = .6 ………9è 3
分
6 3 3 6 3 2
故b = c A
2π
= . S 1, 所以 = bcsinA 3= b2VABC = 3 ,所以b = c = 2 .在 △ABD 中,由余弦定理可得3 2 4
BD2 = AB2 + AD2 - 2AB × AD cos 2π 22 12 2 2 1 ( 1× = + - - )2 = 7,
3 2
即BD = 7 ..………15 分
18.(1)在正方形 ABCD中,点E ,F 分别是 AB ,CD的中点,所以BE / /FD,且BE = FD,故四边形BEDF 为平行四
边形,于是BF / /ED.在四棱锥 A - BCDE 中,BF 平面 ADE ,ED 平面 ADE ,所以BF // 平面 ADE ;………3 分
(2)当VACD为正三角形时,因为点F 是CD的中点,所以 AF ^ CD ,
在正方形 ABCD中,点 E,F 分别是 AB,CD 的中点,故EF ^ CD
又 AFIEF = F , AF 平面 AEF ,EF 平面 AEF ,故CD ^平面 AEF ,
因为CD 平面BCDE ,所以平面 AEF ^ 平面BCDE ;………7 分
(3)在四棱锥 A - BCDE 中,过点A 作 AO ^ EF 于点O,过点O作OG ^ DE 于点G ,连接 AG .
a
在正方形 ABCD中,令 BC = a,则 AE = , EF = a .因为VACD为等边三角形,点F 为CD的中点,
2
AF 3所以 = a ,从而 AE 2 + AF 2 = EF 2 ,即 AE ^ AF 由(2)知,平面 AEF ^ 平面BCDE ,平面 AEF 平面
2
BCDE = EF , AO ^ EF , AO 平面 AEF ,故 AO ^ 平面BCDE ,从而 AO ^ DE .又OG ^ DE, AO OG = O, AO 平面
AOG,OG 平面 AOG ,故DE ^平面 AOG ,而 AG 平面 AOG ,故DE ^ AG ,
所以 AGO 为二面角 A - DE - C 的平面角………10 分
a 3
.在Rt△EAF 中, AO AE × AF
× a 3 1 a
= = 2 2 = a,OE = AE = .
EF a 4 2 4
a a
2 OG DF OE × DF × a
在Rt△DEF 中,EF ^ DF , DE = a2 a 5+ = a ,因为OG ^ DE ,所以 = ,于是OG = = 4 2 = ,
4 2 OE DE DE 5 a 4 5
2
a
3a2 a2 a OG 1
从而在Rt△ AOG 中, AG = AO2 + OG2 = + = ,故 cos AGO = = 4 5 = ,
16 80 5 AG a 4
5
因此,二面角 A - DE
1
- C 的余弦值为 . ………17 分
4
19.(1)(1)取BC 的中点O,连接 AO,OD ,因为侧面 ABC 和底面BCD均为正三角形,所以 AO ^ BC,OD ^ BC ,
又 AO IOD = O, AO,OD 平面 AOD,所以BC ^平面 AOD,
又 AD 平面 AOD,所以BC ^ AD ;………3 分
1
(2)(ⅰ)连接OP ,由l = ,所以 P 为 AD 的中点,由(1)可知BC ^平面 AOD,又OP 平面 AOD,所以
2
BC ^ OP.
所以 POD是二面角P - BC - D 的平面角,
又侧面 ABC 和底面BCD均为正三角形, AB = 2 ,所以OA = OD = 3 ,
所以OP 平分 AOD ,又 AD = 3,
2 2 2
在△AOD AO + OD - AD 3 + 3 - 9 1中,由余弦定理可得cos AOD = = = - ,
2AO ×OD 2 3 2
所以 AOD =120°,所以 POD = 60°,所以二面角P - BC - D 的大小为60°;………7 分
(ⅱ)因为 AC = 2 3 3,又直线 AC 与平面 PBC 所成角的正弦值为 ,所以A 与平面PBC 的距离为 ,
4 2
由(ⅰ)可得 PAO = 30°,由题意,可得 AP = 3l ,
在VAOP 出,由余弦定理可得:
OP 3= AP2 + AO2 - 2AO AP cos30° = 3 + 9l 2 - 2 3 3l = 3 + 9l 2 - 9l ,………10 分
2
由VA-BCP = VC-OPA +VB-OPA ,
1 1 2 3 9l 2 9l 3 1 1可得 + - = 3 3l sin 30° 2,
3 2 2 3 2
1
解得l = .………17 分
3
考试时间:120 分钟,共 150 分
一、单选题(本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
2
1.已知复数 z = ,则( )
1+ i
A. z 的实部为 -1 B. z 的虚部为 i
C. z = 2 D. z =1- i
2.已知一组数据为 20,30,40,50,50,60,70,80,其平均数、第 60 百分位数和众数的大小关系是( )
A.平均数>第 60 百分位数>众数 B.平均数<第 60 百分位数<众数
C.第 60 百分位数<众数<平均数 D.平均数=第 60 百分位数=众数
r r r r r r r r r r
3.已知向量a ,b 满足 a - b = a ×b = 2, a - b = 10 ,则 cos a,b = ( )
2 2 4
A. B 1. 2 C. D.5 3 5
π
4.已知VABC 的内角A , B ,C 的对边分别为 a,b , c, A = ,b = 4 ,下面使得VABC 有两组解的 a的值可以为
3
( )
A.3 B. 13 C.2 D.3 3
5.设 m,n 是两条不同的直线,a , b 是两个不同的平面,给出下列说法,其中正确的是( )
A.若m / /a ,n ^ b ,m ^ n ,则a ^ b
B.若m / /a ,m ^ b ,则a ^ b
C.若m ^ n, m a , n b ,则a ^ b
D.若m ^ a , n b , m ^ n,则a ^ b
6.如图,VA O B 是由斜二测画法得到的VAOB 水平放置的直观图,其中O A = O B = 2 ,点C 为线段 A B 的中点,C
对应原图中的点C ,则在原图中下列说法正确的是( )
uuur uuur
A.OC × AB = 0 B.VAOB 的面积为 2
uuur uuur uuur uuur 5 uuurC.OC 在OB上的投影向量为 2OB D.与 AB 同向的单位向量为 AB
10
7.如图,在棱长为 4 的正方体 ABCD - A1B1C1D1中,M 为棱DD1的中点, N 为棱BC1的中点,设直线 A1D1与平面MNC
交于点Q,则D1Q =( )
3
A.2 B. C.1 D 1.
2 2
8.已知 5 名篮球运动员在某场比赛中的得分均为个位数,且平均数、中位数和极差均为 6,则当方差取最大值时,这组
得分的第 60 百分位数是( )
A.6 B.6.5 C.7 D.7.5
二、多选题(本题共 3 小题,每小题 6 分,共 18 分在每小题给出的选项中,有多项符合题目要求.)
9.下列说法中正确的是(
r )r r r rA r.已知向量 a,b,c ,若 ar/ / b,b / / cr ,则 a / /cr
B r
r r r
.已知非零向量 a,b “ ar, ^ b ” “ ar是 × b = 0 ”的充要条件
uuur uuur uuur
C.若 A,B,P是直线 l上不同的三点,点O在直线 l外,OP = mAP + m - 2 OB m R m 3,那么 =
2
r r r rD.已知非零向量 a,b r,“ a ×b > 0 ”是“ ar,b 夹角为锐角”的必要不充分条件
10.如图,在棱长为 4 的正方体 ABCD - A1B1C1D1中,E 为 AA1的中点,F 为 AE 的中点,则下列结论正确的是( )
A.直线 CE与 A1C1为异面直线 B.CE / /平面BDF
C.三棱锥 E - ABD外接球的体积为 36p D 5 3.二面角 F - BD - E 的余弦值为
9
11.如图,在VABC 中,已知 AB = 4, AC =10, BAC = 60 o,BC 边上的中点为M,AC 边上的中点为 N , AM 、BN 相交
于点 P ,则下列结论正确的是( )
A BC 2 19 B VABC 7 - 19. = . 的内切圆的半径为
3
uuuur uuur
C 4 91. AM 与BN 夹角的余弦值为
91
uuur uuur é 16 ù
D.过点 P 作直线交线段 AB 和BC 于点EF ,则BE × BF 的取值范围是 ê-2, - 9 ú
三、填空题(本题共 3 小题,每小题 5 分,共 15 分.)
12.某学校师生共有 3000 人,现用分层抽样方法抽取一个容量为 225 的样本,已知样本中教师人数为 15 人,则该校学
生人数为 .
13.在直三棱柱 ABC - A1B1C1中,AC ^ BC ,AC = BC = AA1 = 2,动点 P 在棱 B1C1 上,则点 P 到平面 A1BC 的距离为 .
14.在VABC 中, AB = 2AC, D 为边BC 的中点, A的平分线交BC 于点E ,若VADE 的面积为 1,则VABC 的面积
为 ,DE 的最小值为 .
四、解答题(本题共 5 小题,共 77 分,解答应写出文字说明、证明过程或演算步骤.)
15.已知 z
z 1 m
是复数, z + 2i 和 均为实数, z1 = z + - i,其中 i是虚数单位.1- i m m -1
(1)求复数 z 的共轭复数 z ;
(2)若复数 z1 在复平面内对应的点在第一象限,求实数m 的取值范围.
16.随着老年人消费需求从“生存型”向“发展型”转变.消费层次不断提升,“银发经济”成为社会热门话题之一,被各企
业持续关注. 某企业为了解该地老年人消费能力情况,对该地年龄在 60,80 的老年人的年收入按年龄 60,70 , 70,80
分成两组进行分层抽样调查,已知抽取了年龄在 60,70 的老年人500人. 年龄在 70,80 的老年人300人.现作出年龄
在 60,70 的老年人年收入的频率分布直方图(如图所示):
(1)根据频率分布直方图,若每个区间取中点值为代表,估计该地年龄在 60,70 的老年人年收入的平均数及第 95百分位
数;
(2)已知年龄在 60,70 的老年人年收入的方差为3,年龄在 70,80 的老年人年收入的平均数和方差分别为3.75和1.4,试
估计年龄在 60,80 的老年人年收入的方差.
r
17.在VABC 中,角 A,B,C 的对边分别为 a,b,c ,且向量m = 3a - b,a - c nr, = sinA r r+ sinC,sinB ,m / /n .
(1)求角 C ;
(2)若 VABC 的面积为 3,sinB =1+ cosA,点D为边 AC 的中点,求BD的长.
18.如图,在正方形 ABCD 中,点 E,F 分别是 AB,CD 的中点.现将VADE 沿 DE 折起,得到四棱锥 A - BCDE .
(1)证明:BF // 平面 ADE;
(2)当VACD为等边三角形时,证明:平面 AEF ^ 平面 BCDE;
(3)在(2)的条件下,求二面角 A - DE - C 的余弦值.
19.如图,在三棱锥 A - BCD中,侧面 ABC 和底面BCD均为正三角形,且 AB = 2, AD = 3.
(1)求证:BC ^ AD ;
(2)已知 P 在棱 AD 上(不含端点)且 AP = l AD,
l 1(ⅰ)若 = ,求二面角P - BC - D 的大小;
2
3
(ⅱ)若直线 AC 与平面PBC 所成角的正弦值为 ,求实数l 的值.
4
龙岩一中2024-2025 学年下学期高一数学第二次月考参考答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C D A B B D C D BD BCD ACD
12.2800 13. 2 14. 6
2
2
z 2 2(1- i)1.C = = = 1- i ,则 z1 i (1 i)(1 i) 的实部为 1,虚部为-1, z = 2 , z =1+ i .+ + -
1
2.D 平均数为 20 + 30 + 40 + 50 + 50 + 60 + 70 + 80 = 50,Q8 60% = 4.8,\第 5 个数 50 即为第 60 百分位数.众数为
8
50,\它们的大小关系是平均数=第 60 百分位数=众数.
r r 2 r 2 r 2 r r r 2 r 2 r r 2 r 2 r 2 r r r r
3.A a - b = a + b - 2a ×b =10 ,\ a + b =14,Q a - b = a + b - 2 a b = 4,\ a b = 5,
r r r r
cos a,b ar ×b\ = r
2
=
a b 5 .
a b sin B bsin A sin B bsin A4.B 由题意,根据正弦定理有 = ,所以 = ,要使VABC 有两组解,则 = <1,且 a < b ,
sin A sin B a a
即bsin A
π
< a < b ,即 4sin < a < 4,即 2 3 < a < 4,所以选项所给四个数据中只有 13 符合,3
5.B 6.D
7.C 在平面CDD1C1 中,延长CM 交C1D1于 P,连接PN ,交 A1D1于 Q,在VPCC1中,D1M //CC1, D1M =
1 CC
2 1
,则
D1P=C1D1,
1 1
又在△PC1N 中,D1Q//NC1, D1P=C1D1,则D1Q= NC1 = B C =1 .2 4 1 1
8.D 因为这组得分的中位数和极差均为 6,可设这组得分从小到大分别为 a, x,6, y, a + 6 0 a 3 ,因为平均数为 6,可
得 x + y =18 - 2a又因为 x 6 , y a + 6,所以 x + y a +12,所以18 - 2a a +12,所以 a 2,故 2 a 3 .
当 a = 2时,这组得分分别为 2,6,6,8,8.方差:
(2 - 6)2 + (6 - 6)2 + (6 - 6)2 + (8 - 6)2 + (8 - 6)2 16 + 0 + 0 + 4 + 4 24
= = = 4.8
5 5 5
当 a = 3时,要使方差最大,则 x 取最小值 3, y 取最大值 9,这组得分分别为 3,3,6,9,9,
1
: [(3 - 6)2方差 + (3 - 6)2 + (6 - 6)2 + (9 - 6)2 + 9 36- 6)2 ù = = 7.2,此时方差最大.5 5
又由5 60% = 3,所以方差最大时的这组得分的第 60 百分位数是 6 和 9 的平均数 7.5.
9.BD 10.BCD
11 ACD A VABC AB 4 AC =10 1 16 +100 - BC
2
. 对于 ,在 中,且 = , ,由余弦定理得 = ,解得BC = 2 19 ,(负根舍去),
2 2 4 10
1 1
则 A 正确;对于 B,设VABC 的内切圆的半径为 r ,则 C
2 VABC
r = AB AC sin A,即C r = AB AC sin A,
2 VABC
即 (2 19 + 4 +10)r = 4 3 7 3 - 57 10 ,解得 r = ,故 B 错误;对于 C,如图所示,
2 3
以A 为原点,建立平面直角坐标系,易知 A(0,0),C(10,0),设B(x, y) ,
由两点间距离公式得 x2 + y2 =16, (x -10)2 + y2 = 76,解得 x = 2, y = 2 3 ,(负根舍去),
uuuur uuur uuuur uuur
故B(2, 2 3),由中点坐标公式得 N (5, 0) ,M (6, 3),故 AM = (6, 3) ,BN = (3, -2 3) ,设 AM 与BN 的夹角为q ,
故 cosq
18 - 6 12 4 91
= = =
39 21 91 ,故 C 正确;对于 D,易知由于BC 边上的中点为M ,AC 边上36 + ( 3)2 9 + (-2 3)2
BP 2 BE BF
的中点为 N ,而 P 是VABC 两条中线的交点,故 P 是VABC 的重心,所以 = ,设 = p, = q,
BN 3 BA BC
uuur
BP 2
uuur
BN 1
uuur uuur
(BA BC) 1 ( 1
uuur 1 uuur 1 1 1 1 1
= = + = BE + BF )
3 3 3 p q ,由于 P 在直线EF 上,所以
( + ) =1 + = 3
3 p q ,即 p q ,
1 1 2
0 < p 1,0 q 1< 1 1 = 3- 2 1 3 1 9 1 3 9而 ,所以 p , p q ,故得 - ÷ = - - ÷ ,p è p 4 è p 2 4
2 1 1 4 1 1 1
1 3 1 9 1 3 9 1
2 pq = = pq = =
- = - - -
= 2,所以 1 1 1 1 9 , 1 1 1 1 2 ,
p è p
÷ 4 p 2 ÷ è 4
è 2 ÷ ÷ 3- ÷ ÷ 3-è p q
÷
p è p è p q p è p
1
S BE BF sin ABC
故得 VBEF 2
p AB q BC pq 4 1= 1 = =
é , ùê ú,则SVABC sin ABC AB BC AB BC 9 2
2
BE BF pq BE BF
é ù 2 2 2
= = pq é 4 , 1 ùê ú BE
32 19
BF AB + BC - AC 19ê , 4 19 ú cos B = = - ,BA BC 4 2 19 9 2 9 2AB BC 38
uuur uuur uuur uuur 19 uuur uuur é32 19 ù uuur uuur uuur uuurBE × BF =| BE | × | BF | cos B = - | BE | × | BF |由于BE BF ê , 4 19 19,则9 ú BE × BF = - | BE | × | BF | [ 2,
16
- - ],
38 38 9
则 D 正确,
12.2800 13. 2
14. 6 2 在VABC 中,设 A, B,C 对应的边分别为 a,b,c,
2
a
因为D为BC 的中点,所以DC = .因为 AE 为 BAC 的平分线, AB = 2AC ,
2
AB BE
所以 = = 2, EC
BE a
= = ,所以DE = DC - EC
a 1
= ,因为 S
AC EC 2 3 6 VADE
= S =1,所以 S
6 VABC VABC
= 6 .
ì1 ì 2
24
bcsinA = 6,
b = ,
VABC 2 sinAí í a2 b2 c2 2bccosA
24 6 24cosA 30 - 24cosA
在 中, ,所以 ,因为 = + - = + - =
b = 2c c2 6= sinA sinA sinA sinA sinA
30 2 A 2 A sin + cos ÷ - 24 cos
2 A - sin2 A ÷
= è 2 2 è 2 2 A 3
A 1
A A = 27tan + A 18,当且仅当
tan = 时,等号成立,所以 a 3 2 ,所
2sin cos 2 tan 2 3
2 2 2
2
以DE .
2
15.(1)设 z = a + bi(a,b R),则 z + 2i = a + (b + 2)i ,Q z + 2i为实数,\b + 2 = 0 ,解得b = -2,………2 分
z a - 2i (a - 2i)(1+ i) a + 2 a - 2
\ = = = + i a - 2\ = 0
1- i 1- i (1+ i)(1- i) 2 2 为实数, ,解得 a = 2 ………4 分,2
\ z = 2 - 2i,\ z = 2 + 2i;………5 分
1 m 1 m 2m +1 3m - 2
(2)由(1)可知, z1 = z + - i = 2 + -
2 +
÷ i = - i,………8 分m m -1 m è m -1 m m -1
ì2m +1
> 0
Q复数 z
m
1 在复平面内对应的点在第一象限,\í 3m 2 ………10 分 -- > 0
m -1
2
< m <1 m
2
解得 ,故实数 的取值范围为 ,1÷ .……13 分3 è 3
16.(1)平均数为 2 0.04 + 3 0.08 + 4 0.18 + 5 0.26 + 6 0.20 + 7 0.15 + 8 0.05 + 9 0.04 = 5.35 .………3 分
而由于0.04 + 0.08 + 0.18 + 0.26 + 0.20 + 0.15 = 0.91< 0.95,
0.04 + 0.08 + 0.18 + 0.26 + 0.20 + 0.15 + 0.05 = 0.96 > 0.95,
故第95百分位数在区间第95百分位数内,设其为7.5 + x 0 < x <1 .
则0.04 + 0.08 + 0.18 + 0.26 + 0.20 + 0.15 + 0.05x = 0.95,得 x = 0.8 .
所以第95百分位数为7.5 + 0.8 = 8.3 .………7 分
(2)代入数值即知所求方差为
s 2 500 3+ 300 1.4 500 5.35
2 + 300 3.752 500 5.35 + 300 3.75
2
= + - = 3………15 分
500 + 300 500 + 300 è 500 + 300 ÷
r r
17.(1)因为 m // n,所以 3a - b sinB - a - c sinA + sinC = 0,由正弦定理得 a 2+ b 2- c 2= 3ab,
a2 + b2 - c2 3
由余弦定理得 cosC = = 因为C 0, π π,所以C = .………6 分
2ab 2 6
(2)因为 sinB 1 5π 3 1= + cosA,所以 sinB =1+ cos - B ÷ =1- cosB + sinB
1 3
,则 sinB + cosB =1
è 6 2 2 2 2
即 sin
B
π
+ ÷ =1 0 B
5π π B π 7π B π π< < < + < + = π,又 ,所以 ,则 ,所以 B = .6 ………9è 3
分
6 3 3 6 3 2
故b = c A
2π
= . S 1, 所以 = bcsinA 3= b2VABC = 3 ,所以b = c = 2 .在 △ABD 中,由余弦定理可得3 2 4
BD2 = AB2 + AD2 - 2AB × AD cos 2π 22 12 2 2 1 ( 1× = + - - )2 = 7,
3 2
即BD = 7 ..………15 分
18.(1)在正方形 ABCD中,点E ,F 分别是 AB ,CD的中点,所以BE / /FD,且BE = FD,故四边形BEDF 为平行四
边形,于是BF / /ED.在四棱锥 A - BCDE 中,BF 平面 ADE ,ED 平面 ADE ,所以BF // 平面 ADE ;………3 分
(2)当VACD为正三角形时,因为点F 是CD的中点,所以 AF ^ CD ,
在正方形 ABCD中,点 E,F 分别是 AB,CD 的中点,故EF ^ CD
又 AFIEF = F , AF 平面 AEF ,EF 平面 AEF ,故CD ^平面 AEF ,
因为CD 平面BCDE ,所以平面 AEF ^ 平面BCDE ;………7 分
(3)在四棱锥 A - BCDE 中,过点A 作 AO ^ EF 于点O,过点O作OG ^ DE 于点G ,连接 AG .
a
在正方形 ABCD中,令 BC = a,则 AE = , EF = a .因为VACD为等边三角形,点F 为CD的中点,
2
AF 3所以 = a ,从而 AE 2 + AF 2 = EF 2 ,即 AE ^ AF 由(2)知,平面 AEF ^ 平面BCDE ,平面 AEF 平面
2
BCDE = EF , AO ^ EF , AO 平面 AEF ,故 AO ^ 平面BCDE ,从而 AO ^ DE .又OG ^ DE, AO OG = O, AO 平面
AOG,OG 平面 AOG ,故DE ^平面 AOG ,而 AG 平面 AOG ,故DE ^ AG ,
所以 AGO 为二面角 A - DE - C 的平面角………10 分
a 3
.在Rt△EAF 中, AO AE × AF
× a 3 1 a
= = 2 2 = a,OE = AE = .
EF a 4 2 4
a a
2 OG DF OE × DF × a
在Rt△DEF 中,EF ^ DF , DE = a2 a 5+ = a ,因为OG ^ DE ,所以 = ,于是OG = = 4 2 = ,
4 2 OE DE DE 5 a 4 5
2
a
3a2 a2 a OG 1
从而在Rt△ AOG 中, AG = AO2 + OG2 = + = ,故 cos AGO = = 4 5 = ,
16 80 5 AG a 4
5
因此,二面角 A - DE
1
- C 的余弦值为 . ………17 分
4
19.(1)(1)取BC 的中点O,连接 AO,OD ,因为侧面 ABC 和底面BCD均为正三角形,所以 AO ^ BC,OD ^ BC ,
又 AO IOD = O, AO,OD 平面 AOD,所以BC ^平面 AOD,
又 AD 平面 AOD,所以BC ^ AD ;………3 分
1
(2)(ⅰ)连接OP ,由l = ,所以 P 为 AD 的中点,由(1)可知BC ^平面 AOD,又OP 平面 AOD,所以
2
BC ^ OP.
所以 POD是二面角P - BC - D 的平面角,
又侧面 ABC 和底面BCD均为正三角形, AB = 2 ,所以OA = OD = 3 ,
所以OP 平分 AOD ,又 AD = 3,
2 2 2
在△AOD AO + OD - AD 3 + 3 - 9 1中,由余弦定理可得cos AOD = = = - ,
2AO ×OD 2 3 2
所以 AOD =120°,所以 POD = 60°,所以二面角P - BC - D 的大小为60°;………7 分
(ⅱ)因为 AC = 2 3 3,又直线 AC 与平面 PBC 所成角的正弦值为 ,所以A 与平面PBC 的距离为 ,
4 2
由(ⅰ)可得 PAO = 30°,由题意,可得 AP = 3l ,
在VAOP 出,由余弦定理可得:
OP 3= AP2 + AO2 - 2AO AP cos30° = 3 + 9l 2 - 2 3 3l = 3 + 9l 2 - 9l ,………10 分
2
由VA-BCP = VC-OPA +VB-OPA ,
1 1 2 3 9l 2 9l 3 1 1可得 + - = 3 3l sin 30° 2,
3 2 2 3 2
1
解得l = .………17 分
3
同课章节目录
