2025年中考数学复习专练:第十九章 与圆有关的计算(含答案)
文档属性
| 名称 | 2025年中考数学复习专练:第十九章 与圆有关的计算(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 21:25:39 | ||
图片预览



文档简介
第十九章 与圆有关的计算
1.[2024·安徽]若扇形 AOB 的半径为6,∠AOB=120°,则. 的长为 ( )
A.2π B.3π C.4π D.6π
2.[2023·山东东营]若某圆锥侧面展开图的面积是 15π,母线长是5,则这个圆锥的底面圆的半径是 ( )
A.3 B.4 C.5 D.6
3.[2023·安徽]如图,正五边形 ABCDE内接于⊙O,连接OC,OD,则∠BAE-∠COD= ( )
A.60° B.54° C.48° D.36°
4.[2023·四川雅安]如图,某小区要绿化一扇形空地 AOB,准备在小扇形 COD内种花,在其他区域内(阴影部分)种草.现测得∠AOB=120°,OA=15 m,OC=10m,则种草区域的面积为 ( )
5.[2024·四川广安]如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则DE的长为 ( )
A. B.
6.[2023·内蒙古赤峰]某班学生准备表演课本剧,现要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆的周长为20πcm,母线 AB 的长为 30 cm.为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点 A 处开始,绕侧面一周又回到点 A 的彩带(彩带宽度忽略不计),这条彩带的最短长度是 ( )
A.30cm
C.60 cm D.20πcm
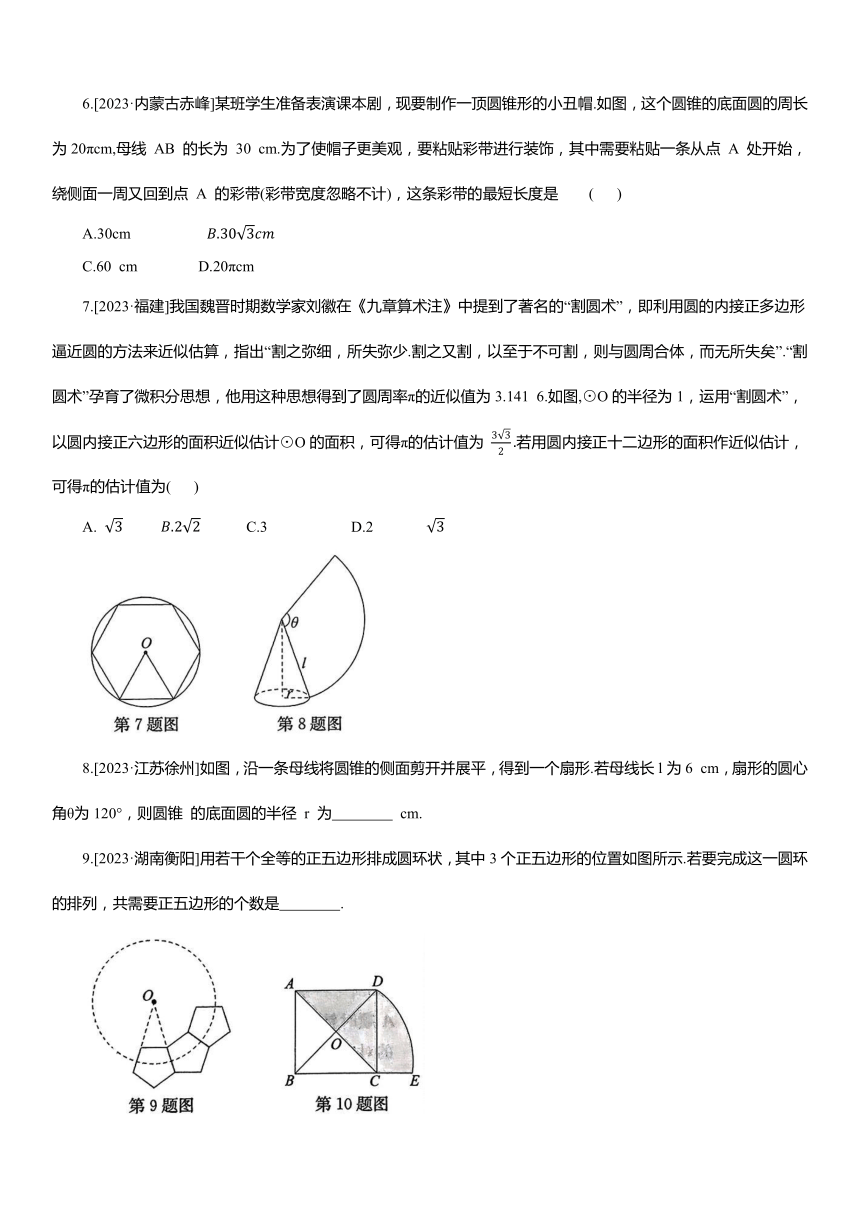
7.[2023·福建]我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形的面积近似估计⊙O的面积,可得π的估计值为 若用圆内接正十二边形的面积作近似估计,可得π的估计值为( )
A. C.3 D.2
8.[2023·江苏徐州]如图,沿一条母线将圆锥的侧面剪开并展平,得到一个扇形.若母线长l为6 cm,扇形的圆心角θ为120°,则圆锥 的底面圆的半径 r 为 cm.
9.[2023·湖南衡阳]用若干个全等的正五边形排成圆环状,其中3个正五边形的位置如图所示.若要完成这一圆环的排列,共需要正五边形的个数是 .
10.[2023·内蒙古包头]如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,以点 B 为圆心,对角线 BD的长为半径画弧,交BC 的延长线于点E,则图中阴影部分的面积为 .
11.[2023·山东潍坊]如图,正方形ABCD内接于⊙O,在 上取一点E,连接AE,DE,过点A作AG⊥AE,交⊙O于点G,交 DE于点F,连接CG,DG.
(1)求证:△AFD≌△CGD;
(2)若AB=2,∠BAE=30°,求图中阴影部分的面积.
12.[2023·湖南怀化]如图,AB 是⊙O 的直径,P 是⊙O外一点,PA 与⊙O相切于点A,C为⊙O上一点,连接PO,PC,AC,OC,且PC=PA.
(1)求证:PC为⊙O的切线;
(2)延长PC与AB 的延长线交于点 D,求证:PD·OC=PA·OD;
(3)若∠CAB=30°,OD=8,求图中阴影部分的面积.
2. A 设这个圆锥的底面圆的半径是 R,则其底面圆的周长是2πR,∴这个圆锥侧面展开图的面积是 解得R=3.
3. D ∵五边形ABCDE是正五边形,
B
5. C 如图,连接OD,OE.
∵AB=AC,∴∠ABC=∠C=70°.
∵OE=OB,∴∠OEB=∠ABC=70°,
∴∠OEB=∠C=70°,∴OE∥AC.
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠A=180°-∠ABC-∠C=180°-70°-
的长为
6. B ∵圆锥的底面圆的周长为20πcm,
∴圆锥的侧面展开图(扇形)的弧长为20πcm.
设该扇形的圆心角为n°,
则 解得n=120.
如图, 过点 B 作 BC⊥AA'于点C,
∴这条彩带的最短长度是:
7. C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,过点A作AM⊥OB于点M.
在正十二边形中,
∴正十二边形的面积为
τ的估计值为3.
8.2 由题意,得母线l=6 cm,θ=120°, 解得r=2(cm).
9.10 正五边形每一个内角的度数为 (5-2)=108°,
∴共需要正五边形的个数是:
10.π ∵四边形ABCD是正方形,
∴AO= CO, DO = BO, AD = CD= BC,∠DBE=45°,
∴△AOD≌△COB(SSS),∴S△AOD=S△COB.
∵正方形ABCD的边长为2,
11.解:(1)证明:∵AG⊥AE,
∴∠EAG=90°,∴∠EDG=∠EAG=90°.
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°.
∵∠ADF+∠FDC=∠CDG+∠FDC=90°,
∴∠ADF=∠CDG.
在△AFD和△CGD中,
∴△AFD≌△CGD(ASA).
(2)如图,过点D作DH⊥AG于点H,连接OA,OD.
∵四边形ABCD是正方形,
∴∠BAD=90°,∠AOD=90°,
∵∠EAG=90°,
∴∠DAG+∠BAG=∠BAE+∠BAG,
∴∠DAG=∠BAE=30°.
由(1),得∠EDG=90°.
∵DH⊥AG,
∴∠DHG=90°,
∴△HDG和△DFG都是等腰直角三角形.
在Rt△ADH中,∠DAG=30°,
∴AG=AH+HG=AH+DH= +1,
∵OA=OD,∠AOD=90°,
∴△AOD是等腰直角三角形,
12.解:(1)证明:∵AB为⊙O的直径,PA为⊙O的切线,
∴PA⊥OA,即∠PAO=90°.
∵点C在⊙O上,∴OC=OA.
在△POC和△POA 中,
(CPCC=PAA,∴△OC≌△POA(SS).
∴∠PCO=∠PAO=90°,即PC⊥OC.
又OC为⊙O的半径,∴PC为⊙O的切线.
(2)证明:由(1)可知OC⊥PD,
∴∠DCO=∠DAP=90°.
∵∠ODC=∠PDA,
∴△ODC∽△PDA,
即 PD·OC=PA·OD.
(3)如图,连接BC,过点C作CE⊥OB于点E.
∵∠CAB=30°,
∴∠COB=60°.
又OC=OB,
∴△OCB为等边三角形.
∵CE⊥OB,
∴OE=BE.
设OE=a,则OA=OB=OC=2a.
在Rt△OCE中,OE=a,OC=2a,
由勾股定理,得
∵OD=8,∴DE=OD-OE=8-a.
在Rt△CDE中,CE= a,DE=8-a,
由勾股定理,得
在Rt△DOC中,OC=2a,OD=8,由勾股定理,得(
,解得a=2,
1.[2024·安徽]若扇形 AOB 的半径为6,∠AOB=120°,则. 的长为 ( )
A.2π B.3π C.4π D.6π
2.[2023·山东东营]若某圆锥侧面展开图的面积是 15π,母线长是5,则这个圆锥的底面圆的半径是 ( )
A.3 B.4 C.5 D.6
3.[2023·安徽]如图,正五边形 ABCDE内接于⊙O,连接OC,OD,则∠BAE-∠COD= ( )
A.60° B.54° C.48° D.36°
4.[2023·四川雅安]如图,某小区要绿化一扇形空地 AOB,准备在小扇形 COD内种花,在其他区域内(阴影部分)种草.现测得∠AOB=120°,OA=15 m,OC=10m,则种草区域的面积为 ( )
5.[2024·四川广安]如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则DE的长为 ( )
A. B.
6.[2023·内蒙古赤峰]某班学生准备表演课本剧,现要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆的周长为20πcm,母线 AB 的长为 30 cm.为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点 A 处开始,绕侧面一周又回到点 A 的彩带(彩带宽度忽略不计),这条彩带的最短长度是 ( )
A.30cm
C.60 cm D.20πcm
7.[2023·福建]我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形的面积近似估计⊙O的面积,可得π的估计值为 若用圆内接正十二边形的面积作近似估计,可得π的估计值为( )
A. C.3 D.2
8.[2023·江苏徐州]如图,沿一条母线将圆锥的侧面剪开并展平,得到一个扇形.若母线长l为6 cm,扇形的圆心角θ为120°,则圆锥 的底面圆的半径 r 为 cm.
9.[2023·湖南衡阳]用若干个全等的正五边形排成圆环状,其中3个正五边形的位置如图所示.若要完成这一圆环的排列,共需要正五边形的个数是 .
10.[2023·内蒙古包头]如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,以点 B 为圆心,对角线 BD的长为半径画弧,交BC 的延长线于点E,则图中阴影部分的面积为 .
11.[2023·山东潍坊]如图,正方形ABCD内接于⊙O,在 上取一点E,连接AE,DE,过点A作AG⊥AE,交⊙O于点G,交 DE于点F,连接CG,DG.
(1)求证:△AFD≌△CGD;
(2)若AB=2,∠BAE=30°,求图中阴影部分的面积.
12.[2023·湖南怀化]如图,AB 是⊙O 的直径,P 是⊙O外一点,PA 与⊙O相切于点A,C为⊙O上一点,连接PO,PC,AC,OC,且PC=PA.
(1)求证:PC为⊙O的切线;
(2)延长PC与AB 的延长线交于点 D,求证:PD·OC=PA·OD;
(3)若∠CAB=30°,OD=8,求图中阴影部分的面积.
2. A 设这个圆锥的底面圆的半径是 R,则其底面圆的周长是2πR,∴这个圆锥侧面展开图的面积是 解得R=3.
3. D ∵五边形ABCDE是正五边形,
B
5. C 如图,连接OD,OE.
∵AB=AC,∴∠ABC=∠C=70°.
∵OE=OB,∴∠OEB=∠ABC=70°,
∴∠OEB=∠C=70°,∴OE∥AC.
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠A=180°-∠ABC-∠C=180°-70°-
的长为
6. B ∵圆锥的底面圆的周长为20πcm,
∴圆锥的侧面展开图(扇形)的弧长为20πcm.
设该扇形的圆心角为n°,
则 解得n=120.
如图, 过点 B 作 BC⊥AA'于点C,
∴这条彩带的最短长度是:
7. C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,过点A作AM⊥OB于点M.
在正十二边形中,
∴正十二边形的面积为
τ的估计值为3.
8.2 由题意,得母线l=6 cm,θ=120°, 解得r=2(cm).
9.10 正五边形每一个内角的度数为 (5-2)=108°,
∴共需要正五边形的个数是:
10.π ∵四边形ABCD是正方形,
∴AO= CO, DO = BO, AD = CD= BC,∠DBE=45°,
∴△AOD≌△COB(SSS),∴S△AOD=S△COB.
∵正方形ABCD的边长为2,
11.解:(1)证明:∵AG⊥AE,
∴∠EAG=90°,∴∠EDG=∠EAG=90°.
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°.
∵∠ADF+∠FDC=∠CDG+∠FDC=90°,
∴∠ADF=∠CDG.
在△AFD和△CGD中,
∴△AFD≌△CGD(ASA).
(2)如图,过点D作DH⊥AG于点H,连接OA,OD.
∵四边形ABCD是正方形,
∴∠BAD=90°,∠AOD=90°,
∵∠EAG=90°,
∴∠DAG+∠BAG=∠BAE+∠BAG,
∴∠DAG=∠BAE=30°.
由(1),得∠EDG=90°.
∵DH⊥AG,
∴∠DHG=90°,
∴△HDG和△DFG都是等腰直角三角形.
在Rt△ADH中,∠DAG=30°,
∴AG=AH+HG=AH+DH= +1,
∵OA=OD,∠AOD=90°,
∴△AOD是等腰直角三角形,
12.解:(1)证明:∵AB为⊙O的直径,PA为⊙O的切线,
∴PA⊥OA,即∠PAO=90°.
∵点C在⊙O上,∴OC=OA.
在△POC和△POA 中,
(CPCC=PAA,∴△OC≌△POA(SS).
∴∠PCO=∠PAO=90°,即PC⊥OC.
又OC为⊙O的半径,∴PC为⊙O的切线.
(2)证明:由(1)可知OC⊥PD,
∴∠DCO=∠DAP=90°.
∵∠ODC=∠PDA,
∴△ODC∽△PDA,
即 PD·OC=PA·OD.
(3)如图,连接BC,过点C作CE⊥OB于点E.
∵∠CAB=30°,
∴∠COB=60°.
又OC=OB,
∴△OCB为等边三角形.
∵CE⊥OB,
∴OE=BE.
设OE=a,则OA=OB=OC=2a.
在Rt△OCE中,OE=a,OC=2a,
由勾股定理,得
∵OD=8,∴DE=OD-OE=8-a.
在Rt△CDE中,CE= a,DE=8-a,
由勾股定理,得
在Rt△DOC中,OC=2a,OD=8,由勾股定理,得(
,解得a=2,
同课章节目录
