2025年中考数学复习专练:第十八章 圆的性质及与圆有关的位置关系(含答案)
文档属性
| 名称 | 2025年中考数学复习专练:第十八章 圆的性质及与圆有关的位置关系(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 238.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 21:32:31 | ||
图片预览




文档简介
第十八章 圆的性质及与圆有关的位置关系
1.[2023·山东泰安]如图,AB是⊙O的直径,D,C是⊙O上的点,∠ADC=115°,则∠BAC的度数是 ( )
A.25° B.30°
C.35° D.40°
2.[2024·湖南长沙]如图,在⊙O 中,弦AB 的长为 8,圆心 O 到 AB 的距离OE=4,则⊙O的半径长为 ( )
A.4 B.4 C.5 D.5
3.[2023·四川眉山]如图,AB切⊙O于点B,连接OA 交⊙O于点C,BD∥OA交⊙O于点 D,连接CD.若∠OCD=25°,则∠A 的度数为 ( )
A.25° B.35°
C.40° D.45°
4.[2023·辽宁鞍山]如图,AC,BC为⊙O的两条弦,D,G分别为AC,BC的中点,⊙O的半径为2.若∠C=45°,则 DG 的长为 ( )
A.2 B.
C. D.
5.[2023·广东广州]如图,△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F.若⊙I 的半径为r,∠A=α,则BF+CE--BC的值和∠FDE 的度数分别为 ( )
A.2r,90°-α B.0,90°-α
C.2r,90°-α2
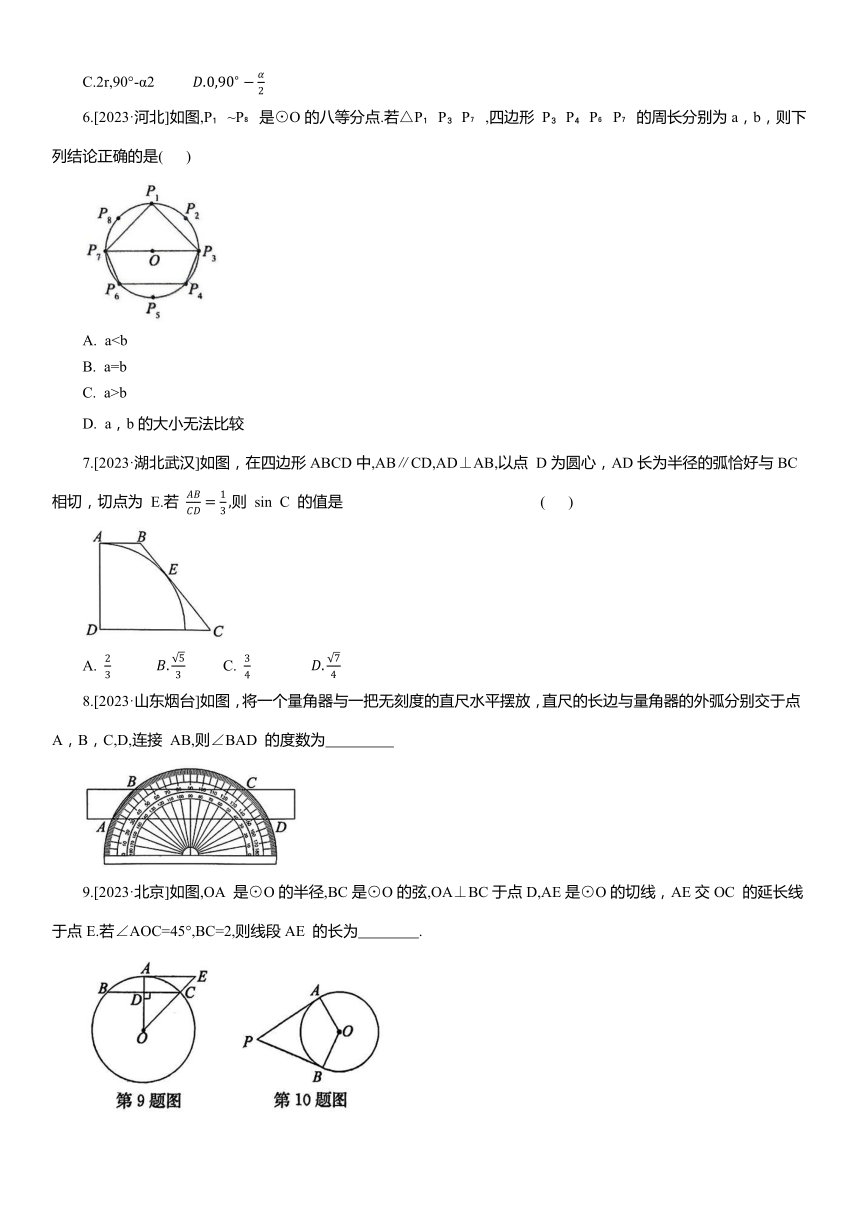
6.[2023·河北]如图,P ~P 是⊙O的八等分点.若△P P P ,四边形 P P P P 的周长分别为a,b,则下列结论正确的是( )
A. aB. a=b
C. a>b
D. a,b的大小无法比较
7.[2023·湖北武汉]如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点 D为圆心,AD长为半径的弧恰好与BC 相切,切点为 E.若 则 sin C 的值是 ( )
A. C.
8.[2023·山东烟台]如图,将一个量角器与一把无刻度的直尺水平摆放,直尺的长边与量角器的外弧分别交于点 A,B,C,D,连接 AB,则∠BAD 的度数为
9.[2023·北京]如图,OA 是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交OC 的延长线于点E.若∠AOC=45°,BC=2,则线段AE 的长为 .
10.[2023·山东滨州]如图,PA,PB 分别与⊙O相切于A,B 两点,且∠APB=56°.若C是⊙O上异于点A,B的一点,则∠ACB的度数为 .
11.[2023·浙江宁波]如图,在 Rt△ABC中,∠C=90°,E 为边AB 上一点,以AE为直径的半圆O 与BC 相切于点D,连接AD,BE=3,BD=3 . P是边AB 上的动点,当△ADP 为等腰三角形时,AP 的长为 .
12.[2023·山东东营]如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=2 求 BD的长.
13.[2023·湖南衡阳]如图,AB 是⊙O 的直径,AC是一条弦,D 是 的中点,DE⊥AB于点E,交AC于点 F,交⊙O于点H,DB交AC 于点G.
(1)求证:AF=DF;
(2)若 求⊙O的半径.
14.[2023·四川宜宾]如图,以AB为直径的⊙O上有两点E,F, 过点E作直线CD⊥AF 交 AF 的延长线于点 D,交AB的延长线于点 C,过点 C作CM平分∠ACD交AE于点 M,交 BE于点 N.
(1)求证:CD是⊙O的切线;
(2)求证:EM=EN;
(3)如果 N 是CM 的中点,且 AB=9 ,求EN的长.
第十八章 圆的性质及与圆有关的位置关系
1. A ∵∠ADC=115°,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠BAC=90°-∠ABC=90°-65°=25°.
2. B ∵OE⊥AB,∴AE=EB=4,
3. C 如图,连接OB.
∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°.
∵BD∥OA,∠OCD=25°,
∴∠D=∠OCD=25°,
∴∠O=2∠D=50°,
4. D 如图,连接AO,BO,AB.
∵∠C=45°,
∴∠AOB=2∠C=90°.
∵⊙O的半径为2,
∴AO=BO=2,
∵D,G分别为AC,BC的中点,
5. D 如图,连接IE,IF.
∵△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,
∴BF=BD,CD=CE,IF⊥AB,IE⊥AC,
∴BF+CE-BC=BD+CD-BC=BC-BC=0,∠AFI=∠AEI=90°,∴∠EIF=180°-α,
6. A 如图,连接P P ,P P .
∵P ~P 是⊙O的八等分点,
∴b-a>0,∴a7. B 如图,连接DB,DE.
设AB=m.
∵B= ,∴CD=3AB=3m.
由题意可知AD⊥AB,BC⊥DE,
∴EB=AB=m,∠CBD=∠ABD.
∵AB∥CD,∴∠ABD=∠CDB,
∴∠CBD=∠CDB,∴CB=CD=3m,
∴CE=CB-EB=3m-m=2m.
∵∠CED=90°,
8.52.5° 如图,设量角器的圆心是 O,连接OD,OB.
9. ∵OA是⊙O的半径,AE是⊙O的切线,
∴∠OAE=90°.
∵∠AOC=45°,OA⊥BC,
∴△CDO和△EAO是等腰直角三角形,
∴OD=CD,OA=AE.
10.62°或118° 如图,连接CA,BC.
∵PA,PB分别与⊙O相切于A,B两点,
∴∠PAO=∠PBO=90°.
∵∠AOB+∠PAO+∠PBO+∠APB=360°,
∴∠AOB=360°-∠PAO-∠PBO-∠APB=
由圆周角定理,知
当点C在劣弧AB上时,
由圆内接四边形的性质,得∠ACB=118°.
综上所述,∠ACB的度数为 62°或118°.
11.6或 如图,连接OD,DE.
∵半圆O与BC 相切于点D,
∴OD⊥BC.
在Rt△OBD中,OB=OE+BE=OD+3,BD=
解得OD=6,∴AO=EO=OD=6.
①如图1,当AP=DP时,点 P 与点O重合,
∴AP=AO=6.
②如图2,当. 时,
∵∠C=90°,∴AC⊥BC,
∴OD∥AC,∴△BOD∽△BAC,
解得AC=10,CD=2
③如图2,当. 时,点 P"在线段AB 的延长线上,
∴不存在DP=AD的情况.
综上所述,当△ADP 为等腰三角形时,AP的长为6或
12.解:(1)证明:如图,连接OD.
∵OD=OB,
∴∠ODB=∠B.∵AB=AC,∴∠B=∠C,
∴∠ODB=∠C,∴OD∥AC.∵DE⊥AC,
∴∠ODE=∠CED=90°,∴DE⊥OD.
∵OD是⊙O的半径,∴DE是⊙O的切线.
(2)如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,∴AD⊥BC.
∵AB=AC,∴BD=CD=2
∴BD的长是2
13.解:(1)证明:∵D是 的中点,
∵AB⊥DH,且AB是⊙O的直径,
∴CD=AH,∴∠ADH=∠CAD,∴AF=DF.
(2)∵AB是⊙O的直径,∴∠ADB=90°,
∴∠DAB+∠B=90°.
∵∠DAE+∠ADE=90°,∴∠ADE=∠B,
设AE=x,则DE=2x.
解得x =0(不合题意,舍去),
∴⊙O的半径为5.
14.解:(1)证明:如图,连接OE.
∵BE=EF,∴∠FAE=∠EAB.
∵OA=OE,∴∠AEO=∠EAB,
∴∠FAE=∠AEO,∴AF∥OE.
∵CD⊥AF,∴OE⊥CD.
∵OE是⊙O的半径,
∴CD是⊙O的切线.
(2)证明:∵AB是⊙O的直径,
∴∠AEB=90°,∴∠AEO+∠OEB=90°.
由(1),知CD是⊙O的切线,
∴∠CEB+∠OEB=90°,
∴∠AEO=∠EAB=∠CEB.
∵CM平分∠ACD,∴∠ECM=∠ACM,
∴∠CEB+∠ECM=∠EAB+∠ACM,
∴∠ENM=∠EMN,∴EM=EN.
(3)由(2),知EM=EN,∠EMN=∠ENM,
∴∠EMN=∠BNC.
∵∠ECM=∠BCN,∴△EMC∽△BNC,
∵N是CM的中点,
∴EM=2BN,CE=2BC.
∵∠BEC=∠EAB,∠BCE=∠ECA,
∴△BEC∽△EAC,
∴AE=2BE.
在Rt△ABE中,
解得BE=9(负值舍去).
∵EN=EM=2BN,
∴EN的长为6.
1.[2023·山东泰安]如图,AB是⊙O的直径,D,C是⊙O上的点,∠ADC=115°,则∠BAC的度数是 ( )
A.25° B.30°
C.35° D.40°
2.[2024·湖南长沙]如图,在⊙O 中,弦AB 的长为 8,圆心 O 到 AB 的距离OE=4,则⊙O的半径长为 ( )
A.4 B.4 C.5 D.5
3.[2023·四川眉山]如图,AB切⊙O于点B,连接OA 交⊙O于点C,BD∥OA交⊙O于点 D,连接CD.若∠OCD=25°,则∠A 的度数为 ( )
A.25° B.35°
C.40° D.45°
4.[2023·辽宁鞍山]如图,AC,BC为⊙O的两条弦,D,G分别为AC,BC的中点,⊙O的半径为2.若∠C=45°,则 DG 的长为 ( )
A.2 B.
C. D.
5.[2023·广东广州]如图,△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F.若⊙I 的半径为r,∠A=α,则BF+CE--BC的值和∠FDE 的度数分别为 ( )
A.2r,90°-α B.0,90°-α
C.2r,90°-α2
6.[2023·河北]如图,P ~P 是⊙O的八等分点.若△P P P ,四边形 P P P P 的周长分别为a,b,则下列结论正确的是( )
A. a
C. a>b
D. a,b的大小无法比较
7.[2023·湖北武汉]如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点 D为圆心,AD长为半径的弧恰好与BC 相切,切点为 E.若 则 sin C 的值是 ( )
A. C.
8.[2023·山东烟台]如图,将一个量角器与一把无刻度的直尺水平摆放,直尺的长边与量角器的外弧分别交于点 A,B,C,D,连接 AB,则∠BAD 的度数为
9.[2023·北京]如图,OA 是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交OC 的延长线于点E.若∠AOC=45°,BC=2,则线段AE 的长为 .
10.[2023·山东滨州]如图,PA,PB 分别与⊙O相切于A,B 两点,且∠APB=56°.若C是⊙O上异于点A,B的一点,则∠ACB的度数为 .
11.[2023·浙江宁波]如图,在 Rt△ABC中,∠C=90°,E 为边AB 上一点,以AE为直径的半圆O 与BC 相切于点D,连接AD,BE=3,BD=3 . P是边AB 上的动点,当△ADP 为等腰三角形时,AP 的长为 .
12.[2023·山东东营]如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=2 求 BD的长.
13.[2023·湖南衡阳]如图,AB 是⊙O 的直径,AC是一条弦,D 是 的中点,DE⊥AB于点E,交AC于点 F,交⊙O于点H,DB交AC 于点G.
(1)求证:AF=DF;
(2)若 求⊙O的半径.
14.[2023·四川宜宾]如图,以AB为直径的⊙O上有两点E,F, 过点E作直线CD⊥AF 交 AF 的延长线于点 D,交AB的延长线于点 C,过点 C作CM平分∠ACD交AE于点 M,交 BE于点 N.
(1)求证:CD是⊙O的切线;
(2)求证:EM=EN;
(3)如果 N 是CM 的中点,且 AB=9 ,求EN的长.
第十八章 圆的性质及与圆有关的位置关系
1. A ∵∠ADC=115°,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠BAC=90°-∠ABC=90°-65°=25°.
2. B ∵OE⊥AB,∴AE=EB=4,
3. C 如图,连接OB.
∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°.
∵BD∥OA,∠OCD=25°,
∴∠D=∠OCD=25°,
∴∠O=2∠D=50°,
4. D 如图,连接AO,BO,AB.
∵∠C=45°,
∴∠AOB=2∠C=90°.
∵⊙O的半径为2,
∴AO=BO=2,
∵D,G分别为AC,BC的中点,
5. D 如图,连接IE,IF.
∵△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,
∴BF=BD,CD=CE,IF⊥AB,IE⊥AC,
∴BF+CE-BC=BD+CD-BC=BC-BC=0,∠AFI=∠AEI=90°,∴∠EIF=180°-α,
6. A 如图,连接P P ,P P .
∵P ~P 是⊙O的八等分点,
∴b-a>0,∴a
设AB=m.
∵B= ,∴CD=3AB=3m.
由题意可知AD⊥AB,BC⊥DE,
∴EB=AB=m,∠CBD=∠ABD.
∵AB∥CD,∴∠ABD=∠CDB,
∴∠CBD=∠CDB,∴CB=CD=3m,
∴CE=CB-EB=3m-m=2m.
∵∠CED=90°,
8.52.5° 如图,设量角器的圆心是 O,连接OD,OB.
9. ∵OA是⊙O的半径,AE是⊙O的切线,
∴∠OAE=90°.
∵∠AOC=45°,OA⊥BC,
∴△CDO和△EAO是等腰直角三角形,
∴OD=CD,OA=AE.
10.62°或118° 如图,连接CA,BC.
∵PA,PB分别与⊙O相切于A,B两点,
∴∠PAO=∠PBO=90°.
∵∠AOB+∠PAO+∠PBO+∠APB=360°,
∴∠AOB=360°-∠PAO-∠PBO-∠APB=
由圆周角定理,知
当点C在劣弧AB上时,
由圆内接四边形的性质,得∠ACB=118°.
综上所述,∠ACB的度数为 62°或118°.
11.6或 如图,连接OD,DE.
∵半圆O与BC 相切于点D,
∴OD⊥BC.
在Rt△OBD中,OB=OE+BE=OD+3,BD=
解得OD=6,∴AO=EO=OD=6.
①如图1,当AP=DP时,点 P 与点O重合,
∴AP=AO=6.
②如图2,当. 时,
∵∠C=90°,∴AC⊥BC,
∴OD∥AC,∴△BOD∽△BAC,
解得AC=10,CD=2
③如图2,当. 时,点 P"在线段AB 的延长线上,
∴不存在DP=AD的情况.
综上所述,当△ADP 为等腰三角形时,AP的长为6或
12.解:(1)证明:如图,连接OD.
∵OD=OB,
∴∠ODB=∠B.∵AB=AC,∴∠B=∠C,
∴∠ODB=∠C,∴OD∥AC.∵DE⊥AC,
∴∠ODE=∠CED=90°,∴DE⊥OD.
∵OD是⊙O的半径,∴DE是⊙O的切线.
(2)如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,∴AD⊥BC.
∵AB=AC,∴BD=CD=2
∴BD的长是2
13.解:(1)证明:∵D是 的中点,
∵AB⊥DH,且AB是⊙O的直径,
∴CD=AH,∴∠ADH=∠CAD,∴AF=DF.
(2)∵AB是⊙O的直径,∴∠ADB=90°,
∴∠DAB+∠B=90°.
∵∠DAE+∠ADE=90°,∴∠ADE=∠B,
设AE=x,则DE=2x.
解得x =0(不合题意,舍去),
∴⊙O的半径为5.
14.解:(1)证明:如图,连接OE.
∵BE=EF,∴∠FAE=∠EAB.
∵OA=OE,∴∠AEO=∠EAB,
∴∠FAE=∠AEO,∴AF∥OE.
∵CD⊥AF,∴OE⊥CD.
∵OE是⊙O的半径,
∴CD是⊙O的切线.
(2)证明:∵AB是⊙O的直径,
∴∠AEB=90°,∴∠AEO+∠OEB=90°.
由(1),知CD是⊙O的切线,
∴∠CEB+∠OEB=90°,
∴∠AEO=∠EAB=∠CEB.
∵CM平分∠ACD,∴∠ECM=∠ACM,
∴∠CEB+∠ECM=∠EAB+∠ACM,
∴∠ENM=∠EMN,∴EM=EN.
(3)由(2),知EM=EN,∠EMN=∠ENM,
∴∠EMN=∠BNC.
∵∠ECM=∠BCN,∴△EMC∽△BNC,
∵N是CM的中点,
∴EM=2BN,CE=2BC.
∵∠BEC=∠EAB,∠BCE=∠ECA,
∴△BEC∽△EAC,
∴AE=2BE.
在Rt△ABE中,
解得BE=9(负值舍去).
∵EN=EM=2BN,
∴EN的长为6.
同课章节目录
